可对角化的其他判定准则及其应用
谢启鸿
(复旦大学 数学科学学院,上海200433)
1 引 言
矩阵或线性变换的可对角化判定是高等代数的重要知识点. 由于判定准则多, 技巧性强, 故可对角化判定一直是教学和考试中的难点(参考[1]的例4和例5). 一般来说, 判定n维复线性空间V上的线性变换φ或n阶复矩阵A可对角化, 通常有以下六种方法(参考[2]的第六章和第七章以及[3]的第6.2.2节和第7.2.3节):
(D1)φ可对角化的充要条件是φ有n个线性无关的特征向量;
(D2) 若φ有n个不同的特征值, 则φ可对角化;
(D3)φ可对角化的充要条件是V是φ的特征子空间的直和;
(D4)φ可对角化的充要条件是φ有完全的特征向量系, 即对φ的任一特征值, 其几何重数等于其代数重数;
(D5)φ可对角化的充要条件是φ的极小多项式无重根;
(D6)φ可对角化的充要条件是φ的Jordan块都是一阶的, 或等价地,φ的初等因子都是一次多项式.
在内积空间的框架下, 可以证明复正规阵可酉对角化以及实对称阵可正交对角化,因此可以自然地问: 能否利用可对角化的判定准则直接证明复正规阵可对角化以及实对称阵可实对角化呢? 通过探索发现, 现有的判定准则(D1)-(D6)很难实现这一目标. 因此, 本文的主要目的即是给出可对角化的其他判定准则(E1)-(E9)(定理1), 并且作为应用, 给出复正规阵可对角化以及实对称阵可实对角化的直接证明(推论3和推论4).
2 可对角化的其他判定准则
以下总是以线性变换作为对象来阐述和证明结论, 其对应的矩阵版本, 留给读者自己补充完整. 首先, 我们来证明一个具有良好性质的线性变换的大型引理.
引理1设V是数域上的n维线性空间,φ是V上的线性变换, 则以下九个结论等价:
(i)V=Kerφ⊕Imφ;
(ii)V=Kerφ+Imφ;
(iii) Kerφ∩Imφ=0;
(iv) Kerφ=Kerφ2, 或等价地, dimKerφ=dimKerφ2;
(v) Kerφ=Kerφ2=Kerφ3=…,或等价地, dimKerφ=dimKerφ2=dimKerφ3=…;
(vi) Imφ=Imφ2, 或等价地, r(φ)=r(φ2);
(vii) Imφ=Imφ2=Imφ3=…, 或等价地, r(φ)=r(φ2)=r(φ3)=…;
(viii) Kerφ存在φ-不变补空间, 即存在φ-不变子空间U, 使得V=Kerφ⊕U;
(ix) Imφ存在φ-不变补空间, 即存在φ-不变子空间W, 使得V=Imφ⊕W.
证由直和的定义可知(i)⟺(ii)+(iii), 于是(i)⟹(ii)和(i)⟹(iii)都是显然的. 根据交和空间维数公式和线性映射维数公式可知
dim(Kerφ+Imφ)=dimKerφ+dimImφ-dim(Kerφ∩Imφ)
=dimV-dim(Kerφ∩Imφ),
于是(ii)⟺(iii)成立, 从而前三个结论两两等价.
(iii)⟹(iv) 显然Kerφ⊆Kerφ2成立. 任取α∈Kerφ2, 则
φ(α)∈Kerφ∩Imφ=0,
于是φ(α)=0, 即α∈Kerφ, 从而Kerφ2⊆Kerφ也成立, 于是(iv)成立.
(iv)⟹(iii) 任取α∈Kerφ∩Imφ, 则存在β∈V, 使得α=φ(β), 于是
0=φ(α)=φ2(β),
即β∈Kerφ2=Kerφ, 从而α=φ(β)=0, 即(iii)成立.
(v)⟹(iv) 显然成立.
(iv)⟹(v) 设Kerφk=Kerφk+1已对正整数k成立, 先证Kerφk+1=Kerφk+2也成立, 然后用归纳法即得结论. Kerφk+1⊆Kerφk+2是显然的. 任取α∈Kerφk+2, 即
0=φk+2(α)=φk+1(φ(α)),
于是φ(α)∈Kerφk+1=Kerφk, 从而φk+1(α)=φk(φ(α))=0, 即α∈Kerφk+1, 于是Kerφk+2⊆Kerφk+1也成立.
(iii)⟺(vi) 考虑φ在不变子空间Imφ上的限制变换φ|Imφ∶Imφ→Imφ, 由限制的定义可知它的核等于Kerφ∩Imφ, 它的像等于Imφ2. 由于有限维线性空间上的线性变换是单射当且仅当它是满射, 当且仅当它是同构, 故(iii)⟺(vi)成立.
(vii)⟹(vi) 显然成立.
(vi)⟹(vii) 设Imφk=Imφk+1已对正整数k成立, 先证Imφk+1=Imφk+2也成立, 然后用归纳法即得结论. Imφk+2⊆Imφk+1是显然的. 任取α∈Imφk+1, 即存在β∈V, 使得α=φk+1(β). 由于φk(β)∈Imφk=Imφk+1, 故存在γ∈V, 使得φk(β)=φk+1(γ), 于是
α=φk+1(β)=φ(φk(β))=φ(φk+1(γ))=φk+2(γ)∈Imφk+2,
从而Imφk+1⊆Imφk+2也成立.
(i)⟹(viii) 显然成立.
(viii)⟹(i) 先证Imφ⊆U: 任取φ(v)∈Imφ, 由直和分解可设v=v1+u, 其中v1∈Kerφ,u∈U, 则由U的φ-不变性可得
φ(v)=φ(v1)+φ(u)=φ(u)∈U.
考虑不等式
dimV=dim(Kerφ⊕U)=dimKerφ+dimU≥dimKerφ+dimImφ=dimV,
从而只能是U=Imφ, 于是(i)成立.
(i)⟹(ix) 显然成立.
(ix)⟹(i) 先证W⊆Kerφ: 任取w∈W, 则由W的φ-不变性可得φ(w)∈Imφ∩W=0, 即有w∈Kerφ. 考虑不等式
dimV=dim(Imφ⊕W)=dimImφ+dimW≤dimImφ+dimKerφ=dimV,
从而只能是W=Kerφ, 于是(i)成立.
有了引理1做铺垫, 可以证明一系列的可对角化判定准则.
定理1设φ是n维复线性空间V上的线性变换, 则φ可对角化的充要条件是对φ的任一特征值λ0, 下列条件之一成立:
(E1)V=Ker(φ-λ0IV)⊕Im(φ-λ0IV);
(E2)V=Ker(φ-λ0IV)+Im(φ-λ0IV);
(E3) Ker(φ-λ0IV)∩Im(φ-λ0IV)=0;
(E4) Ker(φ-λ0IV)=Ker(φ-λ0IV)2, 或等价地, dimKer(φ-λ0IV)=dimKer(φ-λ0IV)2;
(E5) Ker(φ-λ0IV)=Ker(φ-λ0IV)2=Ker(φ-λ0IV)3=…, 或等价地, dimKer(φ-λ0IV)=dimKer(φ-λ0IV)2=dimKer(φ-λ0IV)3=…;
(E6) Im(φ-λ0IV)=Im(φ-λ0IV)2, 或等价地, r(φ-λ0IV)=r((φ-λ0IV)2);
(E7) Im(φ-λ0IV)=Im(φ-λ0IV)2=Im(φ-λ0IV)3=…, 或等价地, r(φ-λ0IV)=r((φ-λ0IV)2)=r((φ-λ0IV)3)=…;
(E8) Ker(φ-λ0IV)存在φ-不变补空间, 即存在φ-不变子空间U, 使得V=Ker(φ-λ0IV)⊕U;
(E9) Im(φ-λ0IV)存在φ-不变补空间, 即存在φ-不变子空间W, 使得V=Im(φ-λ0IV)⊕W.
证由引理1可知, 无论是充分性还是必要性, 只要选取(E1)-(E9)中的一个等价条件来证明即可.
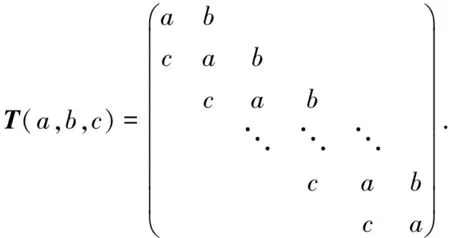
必要性 设φ可对角化, 即存在V的一组基{e1,e2,…,en}, 使得φ在这组基下的表示矩阵为对角阵diag{λ1,λ2,…,λn}, 不妨设λ1=…=λr=λ0,λj≠λ0(r Ker(φ-λ0IV)=L(e1,…,er), Im(φ-λ0IV)=L(er+1,…,en), 于是(E1)成立. 充分性 对应于不同的等价条件, 给出几种不同的证法. 从(E3)出发: 用反证法, 设φ不可对角化, 则由(D6)可知, 存在V的一组基 {e1,e2,…,en}, 使得φ在这组基下的表示矩阵为Jordan标准形 diag{Jr1(λ1),Jr2(λ2),…,Jrk(λk)}, 且至少有一个Jordan块的阶数大于1. 不妨设r1>1, 则由表示矩阵的定义可知 φ(e1)=λ1e1,φ(e2)=e1+λ1e2. 于是(φ-λ1IV)e1=0, (φ-λ1IV)e2=e1, 从而 0≠e1∈Ker(φ-λ1IV)∩Im(φ-λ1IV), 这与已知矛盾. 从(E5)出发: 由Ker(φ-λ0IV)=…=Ker(φ-λ0IV)n可知,λ0的根子空间等于其特征子空间. 因为全空间V可以分解为根子空间的直和, 故全空间V也是特征子空间的直和, 从而由判定准则(D3)即得结论. 从(E5)出发: 由dimKer(φ-λ0IV)=…=dimKer(φ-λ0IV)n可知,λ0的几何重数dimKer(φ-λ0IV)等于其代数重数dimKer(φ-λ0IV)n, 从而由判定准则(D4)即得结论. 从(E5)出发: 设φ的全体不同特征值为λ1,λ2,…,λk,φ的特征多项式为 f(λ)=(λ-λ1)m1(λ-λ2)m2…(λ-λk)mk, 则对任意的α∈V, 由Cayley-Hamilton定理可知 (φ-λ1IV)m1(φ-λ2IV)m2…(φ-λkIV)mk(α)=0, 即(φ-λ2IV)m2…(φ-λkIV)mk(α)∈Ker(φ-λ1IV)m1=Ker(φ-λ1IV), 从而 (φ-λ1IV)(φ-λ2IV)m2…(φ-λkIV)mk(α)=0. 不断这样做下去, 最终可得对任意的α∈V, 总有 (φ-λ1IV)(φ-λ2IV)…(φ-λkIV)(α)=0, 即φ适合多项式g(λ)=(λ-λ1)(λ-λ2)…(λ-λk), 从而由极小多项式的性质可知m(λ)|g(λ). 又由特征值的性质可知g(λ)|m(λ), 于是m(λ)=g(λ)无重根, 从而由判定准则(D5)即得结论. 从(E6)出发: 用反证法, 设φ不可对角化, 则由(D6)可知,φ的Jordan标准形 J=diag{Jr1(λ1),Jr2(λ2),…,Jrk(λk)} 中至少有一个Jordan块的阶数大于1. 不妨设r1>1, 则有r(Jr1(λ1)-λ1Ir1)=r1-1,而r((Jr1(λ1)-λ1Ir1)2)=r1-2. 由矩阵秩的基本不等式可知, r(J-λ1In)>r((J-λ1In)2), 即有r(φ-λ1IV)>r((φ-λ1IV)2), 这与已知矛盾. 推论1设φ是n维复线性空间V上的线性变换, 则φ可对角化的充要条件是V的任一φ-不变子空间都存在φ-不变补空间, 即对任一φ-不变子空间U, 都存在φ-不变子空间W, 使得V=U⊕W. 证充分性可由定理1的(E8)或(E9)得到. 再证必要性, 因为φ可对角化, 故由(D1)可知, 存在V的一组基{e1,e2,…,en}, 它们都是φ的特征向量. 由[2]的推论7.6.3可知,φ在不变子空间U上的限制φ|U也可对角化, 故同理存在U的一组基{α1,…,αr}, 它们也都是φ的特征向量. 由[2]的定理3.5.4(基扩张定理)的证明可知, 可从{e1,e2,…,en}中取出n-r个向量, 不妨设为er+1,…,en, 使得{α1,…,αr,er+1,…,en}成为V的一组新基. 令W=L(er+1,…,en), 则W是φ-不变子空间且满足V=U⊕W. 推论2设φ是数域上n维线性空间V上的线性变换(或A是数域上的n阶方阵), 并且φ(或A)的所有特征值都在中, 则φ(或A)可对角化的判定准则(D1)-(D6)以及(E1)-(E9)在数域上也成立. 证与复数域上的证明完全类似, 具体细节留给读者自己完成. 注1 定理1中的(E3)和(E6)分别是[3]的例7.13和例7.14, 推论1是[3]的例7.15. 将不利用酉相似标准形理论和正交相似标准形理论, 而利用定理1直接证明复正规阵可对角化以及实对称阵可实对角化这两个重要结论. 证这是[3]的例3.72的复版本, 其证明完全类似. 结论得证. 引理4设A为n阶复正规阵,λ0是A的特征值, 则A-λ0In也是复正规阵. 证由复正规阵的定义验证即得. 推论3复正规阵可对角化. 特别地, 实对称阵、实反对称阵、Hermite阵、斜Hermite阵、正交阵、酉阵均可复对角化. 证由引理4, 引理3以及定理1的(E6)即得结论. 引理5实对称阵的特征值全为实数. 证设A为n阶实对称阵,λ0∈是A的任一特征值,α=(a1,a2,…,an)′∈n是对应的特征向量, 即Aα=λ0α.上式两边同时左乘则有注意到α是非零向量, 故注意到A为实对称阵, 故的共轭转置等于它自己, 从而是一个实数, 于是也是实数. 推论4实对称阵在实数域上可对角化. 证1设A为实对称阵, 由[3]的例3.72可得r(A)=r(A2). 再由引理5可知,A的特征值全为实数, 于是根据推论2可得A在实数域上可对角化. 证2由推论3可知实对称阵可复对角化, 又其特征值全为实数, 故实对称阵复相似于实对角阵. 再由[2]的推论7.3.4(相似关系在基域扩张下的不变性)或[4]的定理1可知, 实对称阵可实对角化. 将推论3和推论4合并起来, 可补充如下的可对角化判定准则: (D7) 若复方阵相似于复正规阵, 则可对角化; 若实方阵实相似于实对称阵, 则可实对角化. 先给出一个相似于复正规阵的例子. 证设P为非异阵, 使得P-1AP=Λ为对角阵. 考虑相似变换 再给出一个相似于实对称阵的例子. 例2设a,b,c为实数且bc>0, 证明下列三对角矩阵可实对角化: 因为T(0,1,1)是实对称阵, 故由判定准则(D7)可知T(a,b,c)可实对角化. 本文给出的矩阵或线性变换可对角化的其他判定准则(E1)-(E9)更侧重于可对角化性质在几何层面上的理解, 由此给出了复正规阵可对角化以及实对称阵可实对角化的直接证明, 这些都是通常的可对角化判定准则(D1)-(D6)及其应用的有益补充. 致谢在本文的修改过程中, 得到了审稿人中肯的意见和建议, 在此表示衷心的感谢!3 应 用
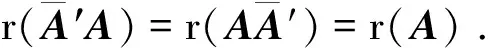
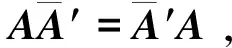
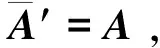
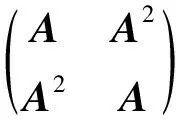
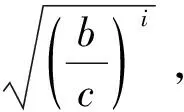
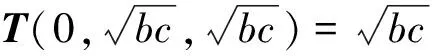
4 结 论

