一类p4阶群的Burnside环之增广商群
李 艳, 常 山
(合肥工业大学 数学学院, 合肥230601)
1 引 言
设G是有限群,记有限G-集X的同构类为[X],并记全体有限G-集的同构类组成的集合为J(G).有限集合之间的不交并和笛卡尔积自然诱导出J(G)中的加法和乘法,G的Burside环Ω(G)定义为J(G)在加法下的完备化[1].
Ω(G)到整数环的一个典范同态ρ∶Ω(G)→,它把有限G-集X的同构类为[X]映为XG的基数,其中XG={x∈X|g·x=x,∀g∈G}.ρ称为Ω(G)的增广映射, 其核称为Ω(G)的增广理想(augmentationideal).用Δn(G)表示Δ(G)的n次幂, 可得Ω(G)中理想的降链:
Ω(G)⊇Δ(G)⊇Δ2(G)⊇…⊇Δn(G)⊇….
称Δn(G)/Δn+1(G)为Ω(G)的第n个增广商群, 记作Qn(G).
讨论Δn(G)与Qn(G)的结构对于研究Burside环十分有意义. 文[2-6]分别针对有限交换群,广义二面体群,两类有限p群确定了相应增广商群的结构,这里p是奇素数.
本文对∀n∈+, 构造了Δn(Ip)作为自由-模的一组基底, 并确定了Qn(Ip)的结构,其中
IP=〈a,b|ap2=bp2=1,b-1ab=ap+1〉
是一个p4阶群. 此外,和本文选题相平行的问题还有表示环的增广理想与增广商群问题[7-8], 所用工具以对角化和单位根为主.
2 预备知识
本节列出若干关于Ω(G)与Δ(G)的基本结论,其中引理1,引理2和引理3刻画了Ω(G)与Δ(G)的加法结构,引理4和引理5刻画了Ω(G)的乘法结构.
引理1传递G-集X同构于G/K,其中K是X中任一元素的固定子群.
引理2设K,L≤G, 则G/K与G/L同构的充分必要条件是K~L.
引理3设Γ是G的子群的共轭类的代表元集合,则Ω(G)作为自由-模以{[G/K]|K∈Γ}为基底,Δ(G)作为自由-模以{[G/K]|K∈Γ,K 引理4设K是G的子群,L是G的正规子群, 则 特别地,[G/G]是Ω(G)中的乘法单位元. 引理5对任意正整数n,Qn(G)总是有限交换群, 因此Δn(G)的自由秩都等于|Γ|-1. 本节给出Ip的所有子群以及它们在共轭关系下的分类, 其中 IP=〈a,b|ap2=bp2=1,b-1ab=ap+1〉, p是奇素数.由Ip的表现易得〈a〉◁Ip,且 Ip=〈a〉∪b〈a〉∪…∪bp2-1〈a〉, 因此Ip中元素可唯一表示为biaj.0≤i,j≤p2-1,从而|Ip|=p4. 由Ip定义立得其包含于〈a〉的子群. 引理6〈a〉共有3个子群{1},〈a〉,〈ap〉, 它们都是Ip的正规子群, 阶分别为1,p2,p. 为了确定Ip不包含于〈a〉的子群, 先证明下列等式. 引理7对任意整数i,j,总有 (i)ajb=baj(p+1); (ii)ajbi=biaijp+j,特别地,abp=bpa,apb=bap,从而ap,bp属于Ip的中心; 证(i) 由Ip的定义知ab=ba1+p,即该等式对j=1成立,假设该等式对j-1成立,于是 ajb=aaj-1b=aba(j-1)(p+1)=ba(p+1)a(j-1)(p+1)=baj(p+1). 即得(i). (ii) 用(i)和归纳法即得.(iii)综合(i),(ii)即得. 以下设K是Ip的真子群,且K⊄〈a〉,则K〈a〉也是Ip的子群且真包含〈a〉,因此|K〈a〉|=p3或p4.记N=K∩〈a〉,所以N⊆〈a〉,由前讨论知N=〈aps〉,s=2,1,0,考察同构 K/N≅k〈a〉/〈a〉,biajNbiaj〈a〉=bi〈a〉. 易见K〈a〉/〈a〉是Ip/〈a〉的子群,而Ip/〈a〉≅〈b〉,因此K〈a〉/〈a〉是一个循环群.不妨设K〈a〉/〈a〉的生成元为bpt〈a〉,其中t=1,0,再设该生成元在上述同构下的原像为bptarN,其中0≤r≤ps-1,则 注意K/N是循环子群要求(bptar)p2-t∈〈aps〉,易见该式当t=0时必定成立, 当t=1时, 应用引理7计算可知要求arp∈〈aps〉,即ps|rp,当s=1,0时显然也成立. 以下根据s与t的取值具体给出K的结构. t=0,s=0时, |K|=p4,舍去; t=1,s=2时, 由p2|rp知p|r,不妨设r=hp,其中0≤h≤p-1,于是 综上所述,已经求出Ip的所有真子群:{1};〈a〉;〈ap〉;〈bam〉,0≤m≤p2-1;〈bpahp〉,0≤h≤p-1;〈ap,bal〉,0≤l≤p-1;〈ap,bpak〉,0≤k≤p-1;〈a,bp〉. 本节的最后来确定Ip的子群之间的共轭关系,已知{1},〈a〉,〈ap〉都是Ip的正规子群,故仅需讨论不包含于Ip的子群.设 再设g=bkal,应用引理7计算知 a-l(buav)al=buav·a-lup,b-k(buav)bk=buav·akvp, 于是 因此前讨论的5类子群之前互不共轭,将这5类子群分别代入讨论可知除第一类之外都是Ip的正规子群,对第一类子群,给出以下引理. 引理8〈bam〉~〈bam′〉的充分必要条件为m≡m′(modp). 证必要性由前讨论可得.对于充分性,由a(bam)a-1=bam+p可知 〈bam〉~〈bap+m〉~〈ba2p+m〉~…~〈ba(p-1)p+m〉, 0≤m≤p-1. 即得. 应用此引理可知第一类子群可分成p个共轭类,代表元可选为〈bam〉,0≤m≤p-1. 综上即得Ip的子群共轭类的一个完全代表元系: Ip,〈a〉,〈ap〉,{1},{〈bp,ahp〉|0≤h≤p-1},{〈ap,bal〉|0≤l≤p-1}, 从而得到Δ(Ip)作为自由-模的一组基底,为了表达的简便,分别记Ip-集的同构类 [Ip/〈a〉],[IP/〈ap〉],[Ip/{1}],[Ip/〈bpahp〉],[Ip/〈ap,bal〉], [Ip/〈ap,bpak〉],[IP/〈bam〉],[Ip/〈a,bp〉] 为α0,α1,α2,γh,ξl,λk,βm,θ,其中0≤h,l,k,m≤p-1. 推论1Δ(Ip)作为自由-模以 本节首先讨论Ω(Ip)的乘法结构,然后对任意正整数n,具体构造Δn(Ip)作为作为自由-模的基底,并确定Qn(Ip)的结构. 定理1对任意的0≤i,j≤2; 0≤h,l,k,m,h′,l′,k′,m′≤p-1,有 (i)αiαj=pmin{i,j}+2·αmax{i,j}; (ii)αiγh=pi+1α2; (v)αiβm=piα2; (vi)αiθ=pαi; (xix)βmθ=γm; (xx)θ2=pθ; 证(i)-(xx)是引理4的直接推论, 故只需证明(xxi).由Ip的定义计算可知 Ip/〈bam〉={ai〈bam〉|0≤i≤p2-1}, 设 x=(ai〈bam〉,aj〈bam′〉)∈Ip/〈bam〉×Ip/〈bam′〉, 其中0≤i,j≤p2-1.计算知x的稳定子群为 ai〈bam〉a-i∩aj〈bam′〉a-j~〈bam〉∩aj-i〈bam′〉ai-j=〈bam〉∩〈bam′+(j-i)p〉. 注意到〈bam〉∩〈bam′+(j-i)p〉是〈bam〉的子群,因此必为〈bam〉,〈(bam)p〉,{1}三者之一,分别对应轨道的同构类α2,βm,γm. ① 当m≠m′时, 计算可知对任意0≤i,j≤p2-1, 总有〈bam〉∩〈bam′+(j-i)p〉={1}.从而βmβm′中每个元所在轨道的同构类都是α2, 计算知共有p4个元, 恰好组成一个轨道, 即得βmβm′=α2. ② 当m=m′,x的稳定子群为〈bam〉∩〈bam′+(j-i)p〉.如果p|(j-i),那么〈bam〉∩〈bam′+(j-i)p〉=〈bam〉. 此时x所在轨道的同构类为βm,易见这样的x共有p3个,恰好组成p个轨道.如果p不整除(j-i), 那么〈bam〉∩〈bam+(j-i)p〉等于〈(bam)p〉或{1},计算可得 (bam+(j-i)p)p=bpamp+(j-i)p2=bpamp=(bam)p, 以下来构造Δn(Ip)作为自由交换群的基.注意到Δ(Ip)的自由秩等于4p+4, 因此由引理5可知, 对任意正整数n,Δn(Ip)的自由秩也是4p+4, 从而仅需构造Δn(Ip)的基数为4p+4的生成元集. 定理2对任意n≥2,Δn(Ip)作为自由-模以 为基底. 证易见Λn的基数为4p+4,故仅需证明Λn是Δn(Ip)的生成元集.为简化叙述, 记Ω(Ip)的子集合Γ生成的加法子群为Γ.对n归纳, 当n=2时, 应用推论1和定理1计算可得 Δ2(Ip)={pi+2αj|0≤i≤j≤2}+{pi+1α2|0≤i≤2} 于是结论对n=2成立.假设n≥3且结论对n-1成立, 即Δn-1(Ip)在加法下是以 为基的自由交换群, 则由Δn(Ip)=Δn-1(Ip)·Δ(Ip)计算可得 Δn(Ip)=Δn-1(Ip)·Δ(Ip) =pn-3 因此结论对任意n≥2都成立, 定理得证. 定理3对任意正整数n, 其中Cp表示p阶循环群. 本文对p4阶群IP=〈a,b|ap2=bp2=1,b-1ab=ap+1〉给出了所有子群并分析了这些子群间的共轭关系,由此刻画出Ω(Ip)与Δ(Ip)的加法与乘法结构,并对任意正整数n,具体构造了Δn(Ip)作为自由-模的基底, 并确定Qn(Ip)的结构.对研究Burside环具有一定的理论意义. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.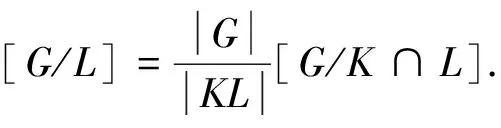
3 子群及其分类
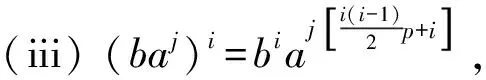

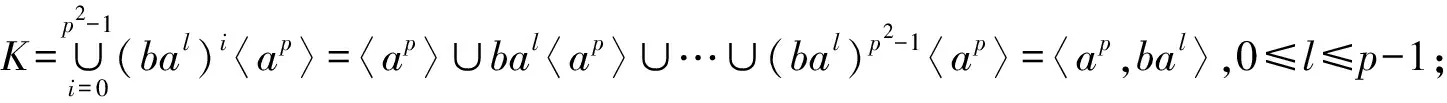
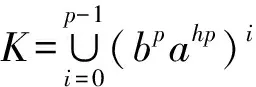
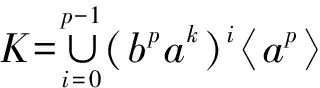
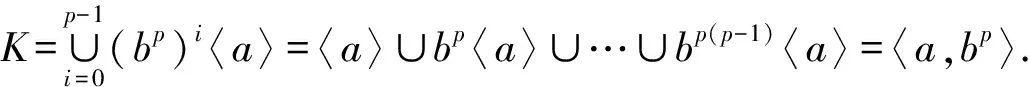
{〈ap,bpak〉|0≤k≤p-1},{〈bam〉|0≤m≤p-1},〈a,bp〉.4 主要结论
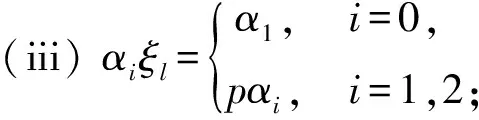
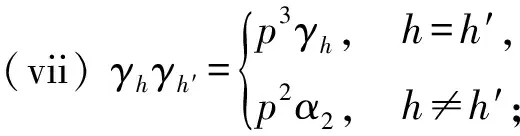

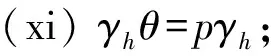
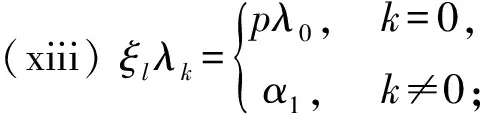
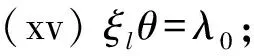
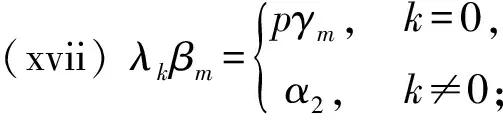
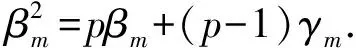
5 结 论

