基于多次反射等效界面模型的海上三维多次波预测与剔除❋

曹艳玲， 赵 波， 吴 波， 李金山， 毛士博， 王倩倩， 都国宁

(1. 山东省第一地质矿产勘查院， 山东 济南 250000； 2. 中国海洋大学海洋地球科学学院， 山东 青岛 266100； 3. 海底科学与探测技术教育部重点实验室， 山东 青岛 266100)

在海上地震勘探中，由于海面和海底为强波阻抗界面，地震波传播过程中容易在海面和海底之间产生多次波，深部强反射界面也易导致自由表面多次波的发育，多次波的存在严重降低了地震数据的信噪比，降低成像剖面的质量，且会误导解释工作，增加油气勘探风险，因此必须对其进行剔除。

目前主流的多次波压制方法有两大类，一类是滤波类多次波剔除算法，另一类是预测减去类算法。滤波类算法主要是利用多次波与一次波在不同域内的差异，利用滤波算法对其进行剔除。Ryu提出利用F-K变换对多次波进行滤波处理[1]；Hampson提出通过最小二乘反演来优化抛物线拉冬域数据的方法[2]，Sacchi等提出一种利用拉冬域稀疏性的高分辨抛物线拉冬变换，得到了很好的多次波压制效果[3]；Moore和Kostov对这一高分辨抛物线拉冬变换方法做了进一步的研究和发展，取得了更好的多次波剔除效果。滤波类算法已在实际生产中得到了广泛应用，但存在以下局限：易假频问题；当多次波和一次波时差较小时，难以实现一次波与多次波的无畸变分离。

预测减去法是一种基于波动理论对多次波进行预测，然后进行匹配相减的一种多次波剔除算法。Berryhill与Wiggins对于使用波场延拓法压制海洋拖缆地震资料中的海底多次波进行了深入研究，有效地压制了海底多次波[4-5]。Bernth和Sonneland于频率-波数域利用波场延拓成功进行了平坦海底多次波预测[6]。针对二维的地震记录，1982年Berkhout提出了一种自由界面多次波预测(Surface-related Multiple Elimination，SRME)方法，该方法考虑了震源和检波器的特性，虽然仅适用于较低频率的信号，但这一近似在实践中获得了较好的应用效果[7-10]；Weglein等[11-13]对SRME算法做了更进一步的研究，使其得到更广泛的应用；Verschuur和Berkhout系统地总结了前人的研究理论，进一步提出了“反馈环”的概念，对海底多次波压制有较好的效果[14]。到目前为止，对于二维地震数据，SRME算法已成为实际生产中多次波剔除的首选，但对于三维地震资料，现有算法难以有效压制远炮检距道中的多次波，而且运算量较大，限制了三维SRME的应用。

不同于以上方法，2005年王修田等提出了利用射线追踪求取海底多次波旅行时，再通过同相轴追踪进行多次波压制的处理方法[16]。这种方法首先利用稳定波束法射线追踪[17]预测各阶海水鸣震的旅行时，然后通过记录重排法将多次波同相轴校平再基于拉冬变换(RT)或SVD分阶等算法进行滤波以消除多次波。该方法不存在空间假频问题，二维情况下，其多次波追踪精度高且计算耗时小，在二维地震数据中取得了较好的多次波剔除效果。然而，将该方法推广至三维海水鸣震压制中却遇到了困难，原因在于：当海底起伏剧烈时，三维空间中多次波的传播路径极其复杂，这大大增加了基于海底模型通过射线追踪预测海水鸣震旅行时的难度。

本文针对海底与自由表面之间的强多次波的压制，提出了一种基于多次反射等效界面模型的多次波追踪与剔除方法，通过构建多次反射等效模型，将多次波复杂的多次反射路径转化为更易射线追踪的一次反射路径，实现了炮集域三维地震多次波的高精度追踪，在此基础上，再通过FK滤波算法实现多次波的有效剔除。该方法避免了常规CMP域多次波剔除时的共面元道集覆盖次数分布不均匀以及动校畸变的问题，能够实现复杂构造区域多次波的高精度追踪与剔除。理论模型检验和海上实际资料的处理结果均验证了该方法的有效性。

1 基于多次反射界面等效模型的三维多次波预测与剔除

1.1 三维界面m阶多次波时距曲面方程的推导

根据斯奈尔定律，地震波的反射角与入射角相等，由此可做出图1所示三维二阶海底多次波传播路径示意图。图1中，O为震源，P为一次反射波的接收点位置，M点为二次反射波的接收点位置，OPM所在平面为海面；R1和R2所在平面为海底E，其中R1为一次波在海底的反射点，R2为二次反射波在海底的反射点，H为O点到海底E的垂点，OH=h，海底倾角为α。地震波由震源O出发，在R1处发生反射后、于点P处被第一次接收，接着又在点R2处发生二次反射、于点M处又被第二次接收，传播路径为O→R1→P→R2→M。

图1 三维倾斜界面的2阶多次波传播路径示意图

为求得关于海底多次反射的等效界面，首先令P点关于海底E的镜像点为P′，则过P′点，倾角为2α的斜截面即为多次反射等效界面，记为E′，则2阶多次波的传播路程等价于由震源O激发的地震波在等效反射界面中点P′处发生反射的一次波路程，即：

OR1+R1P+PR2+R2M=OP′+P′M。

(1)

作震源点O关于界面E′的对称点O′(虚震源点)，则地震波由O点入射到P′点再反射回M点的路程OP′+P′M，等价于由点O′直接传播到M点的距离O′M。

假设三维空间中检波点M的空间坐标为(x,y,z)，则其到震源O的偏移距r为：

(2)

令O′O=h′，则有：

(3)

令xm为虚震源O′在水平面的投影H1到震源O的距离，则有：

(4)

进一步由勾股定理可得：

(5)

假设介质速度为v，则由虚震源原理求得其时距曲面方程可表示为：

(6)

同理可得m阶多次波时距曲面方程为：

(7)

1.2 各阶海底多次反射等效界面模型的建立

为了高效地建立多次反射等效界面，可将三维海底模型分解为若干沿主测线方向的二维“界线”，然后求取其多次反射等效“界线”，最后合成为多次波反射等效界面。对于每条二维海底界线，通常从起伏较为平缓的一侧开始，将每个线元(两个空间采样点之间的线段)的倾角作为海底界面的倾角，据此计算多次反射等效“界线”中的相应线元。

图2给出了沿主测线方向求取多次反射等效“界线”的示意图，其中x轴表示沿主测线方向的水平距离，z轴表示深度，点D1,i、D1,i+1和D1,i+2(变量下标的第一个值是多次波阶次，值为1表示一次波)为海底“界线”中任意的相邻节点，其坐标分别为(x1,i,z1,i)、(x1,i+1,z1,i+1)和(x1,i+2,z1,i+2)，据此求取与上述三点所对应的m阶等效界面深度。

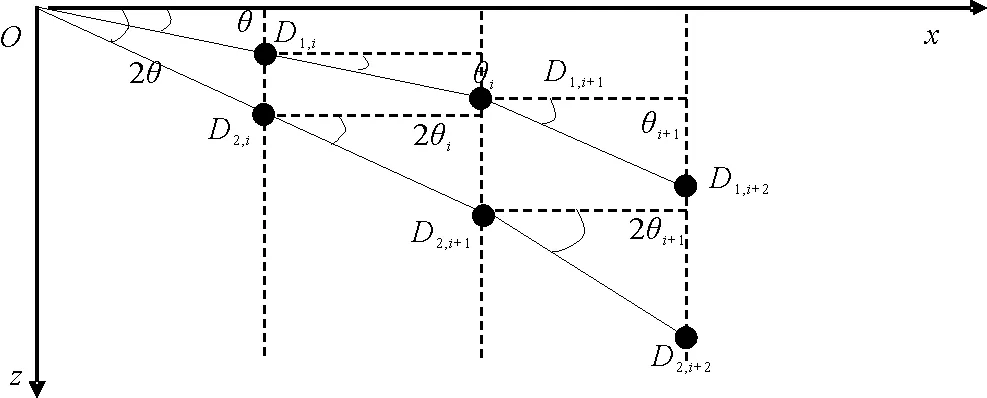
图2 基于主测线方向求取多次反射等效“界线”示意图

(8)

(9)

因此节点D2,i的坐标为D2,i(x1,i,z2,i)。

求出节点D2,i的坐标之后，可据此进一步求取后续节点的深度，则节点D1,i+1下方的等效反射界面深度z2,i+1为：

z2,i=z2,i+|x1,i+1-x1,i|tan2θi。

(10)

因此节点D2,i+1的坐标为D2,i+1(x1,i+1,z2,i+1)。

根据点D1,i+1、D1,i+2的坐标可确定出二者间线元的倾角θi+1，即：

(11)

则节点D1,i+2下方等效反射界面的深度z2,i+2为：

z2,i+2=z2,i+1+|x1,i+2-x1,i+1|tan2θi+1。

(12)

而节点D2,i+2的坐标为D2,i+2(1,i+2,z2,i+2)。依次类推，对海底“界线”中的全部节点进行计算，可获得其2阶多次反射等效“界线”。

可将上述计算2阶多次反射等效“界线”的过程推广到n阶情形，其区别在于m阶多次反射等效“界线”的倾角应为mθi，当海底“界线”节点的深度为z1,i，则其下方m阶等效反射“界线”的深度应为：

(13)

类似地，当已知m阶等效反射“界线”一个节点Dm,i的深度zm,i时，可进一步求取后续节点Dm,i+1的深度zm,i+1，即：

zm,i+1=zm,i+|x1,i+1-x1,i|tanmθi。

(14)

1.3 基于多次反射等效界面的多次波旅行时追踪

为提高射线追踪过程的计算效率，基于野外观测信息截取目标炮集记录所处的局部模型，然后在该局部模型中进行射线追踪以计算各地震道的多次波旅行时。在针对单道记录的射线追踪中，首先通过选取控制点进行试射，从而可大致确定该检波点对应的反射区域，以达到缩小射线搜索范围、提高追踪效率的目的。

针对m阶多次反射等效界面，其多次波旅行时追踪的具体步骤为：

(1)读取单炮记录的炮点和所有检波点坐标，筛选出最大、最小的主测线及联络测线的坐标xmax、xmin、ymax、ymin。

(2)依据筛选的坐标，从建立的各阶多次反射等效界面模型中截取介于主测线坐标x∈(xmin,xmax)范围、联络测线坐标y∈(ymin,ymax)范围间的局部模型。

(3)对于一个反射等效界面，依据适当横、纵坐标间隔选取控制点，并对控制点进行试射，要求射线传播路径满足斯奈尔定律，据此获得其在观测面的出射点。

(4)比较一个检波点与步骤(3)中的出射点坐标，选择距检波点最近的出射点。然后以该出射点对应的试射点为中心，采用更小间隔再次试射并更新搜索区域。通过多次迭代并缩小搜索半径，直至有出射点到检波点的距离小于给定误差，此时将该出射点对应的试射点作为等效界面反射点。

(5)采用地震波在海水中的传播速度，计算由炮点出发至出射点的射线旅行时作为该检波点的多次波旅行时。

1.4 基于FK滤波的炮集域三维海水鸣震衰减

在剔除海水鸣震前，需要依据多次波时距曲线按相同的时窗长度抽取地震数据，并将抽取的数据重排以校平多次波同相轴。在海底多次波同相轴校平后，一次波的同相轴明显弯曲，据此可在重排后的记录中利用FK滤波衰减多次波，并将滤波后的数据放回炮集记录。

图3展示了记录重排过程，图3(a)为重排前单缆的炮集记录，其中彩色曲线为追踪得到的多次波时距曲线，图3(b)为重排后的单缆炮集记录，其中彩色曲线位置的海底多次波同相轴已校正为水平状态。

图3 基于多次波追踪时距曲线的记录重排示例

在对地震记录进行重排后，多次波与一次波同相轴的曲率会因视速度的不同具有较大差异，因此可通过FK滤波[2]去除海水鸣震。FK滤波是将时间—空间域中的地震数据通过二维傅里叶变换转换到频率—波数域，在该域中一次波与多次波会因同相轴倾角的差别而处于不同区域，据此可切除多次波范围，最后将数据反变换回时间—空间域则完成多次波压制。

对时间—空间域的地震数据d(x,t)按照式(12)进行二维傅里叶变换：

(15)

经过上述处理，地震数据变换至频率—波数域，其中kx为水平波数、ω为频率。

图4为炮集记录中同相轴示意图，其中地震波同相轴倾角为α，已知波速为c，则其水平波数kx为：

图4 炮集记录同相轴示意图

(16)

在频率—空间域中切除多次波所在区域，并将滤波后的记录依据式(14)反变换回时间—空间域：

(17)

最后把记录重排的记录放回炮集记录即完成多次波压制。

2 模型实验

首先建立含有复杂构造的三维理论模型，对该模型的地震记录基于海水的波速(1 500 m/s)进行叠前时间偏移，对得到的时间域数据体进行“时深”转换获得深度域数据体，据此建立深度域的海底界面模型。然后依据海底界面建立多次反射等效界面模型，再利用射线追踪技术求取海底多次波旅行时。在此之后，以多次波时距曲线为基准，在重排炮集记录中利用FK滤波进行多次波迭代压制。

建立长、宽及最大深度分别为5 000、5 000及2 000 m的三维层状介质模型，其纵波速度模型切片如图5所示。为了更直观的显示模型结构与速度特征，取过其中心沿主测线方向、联络测线方向的纵波速度模型切片。该模型共包含7套匀速地层，沿主测线方向，模型左部发育以穹隆结构，右侧为凹陷结构，在穹隆两侧均存在断面垂直于主测线方向的两个断层。为使模拟的地震记录中存在较强的海底多次波，使海水层与其下部地层具有较大的速度差(达到500 m/s)，而海底较为平坦，其深度介于100～200 m之间。

图5 理论模型的三维显示示例

为获得准确的海底界面模型，基于海水波速(1 500 m/s)进行叠前时间偏移创建三维叠前偏移数据体，在偏移数据体的所有剖面中，拾取出海底，然后进行时—深转换，据此建立的三维海底深度模型如图6所示。

图6 三维各阶多次反射等效界面模型

对于任一炮集记录，基于等效界面模型进行射线追踪，并将追踪的多次波时距曲线叠置在原始炮集记录中，可知多次波旅行时与原始记录中的多次波同相轴基本吻合，这有效验证了上述追踪过程的正确性。

将各缆数据分别变换到FK域，切除波数kx=0附近区域再反变换回时间域，然后把滤波结果反重排后放回到原始炮集记录中。图7显示了衰减多次波前、后的炮集记录，其中箭头指向的海底多次波已得到较好压制。

图7 压制多次波前后的炮集记录示例

3 实际资料处理效果

用于验证的工区所在海域为硬海底地区，沿纵测线方向海水由浅至深变化(水深介于400～1 000 m)。地震资料采用奇偶炮激发方式，共有95条航线、94 656炮，其它观测参数见表1。

表1 三维海上观测系统参数表

基于海水速度(1 500 m/s)进行三维叠前时间偏移处理，从而获得三维叠前时间偏移数据体，随后通过数字化采样建立三维海底界面模型，再依据该海底模型创建多次反射等效界面模型。依据各阶多次反射等效界面模型，基于射线追踪技术求取多次波旅行时。并将追踪的多次波时距曲线叠置在原始炮集记录中(蓝色曲线)，相应的局部放大图像见图8，经过观察分析可知多次波旅行时与原始记录中的多次波同相轴基本吻合，这有效验证了上述追踪过程的正确性。

图8 利用预测的多次波旅行时进行同相轴追踪示例(炮号：1001)

图9给出了衰减多次波前(a)、后(b)及剔除的多次波(c)的单揽炮集记录，通过对比可知，原始炮集记录中的强鸣震多次波几乎掩盖了同时段的一次波信号，而在衰减多次波后的炮集记录中，这些强多次波基本被消除，振幅较弱的一次波信号得以突显出来，炮集记录的信噪比得到明显提升，从剔除的多次波记录中也看不到明显的一次有效波，也未出现畸变。

图9 压制海水鸣震前、后的炮集记录示例

对衰减多次波前、后的地震记录进行克希霍夫积分叠前时间偏移处理，进而可分析压制多次波前、后的剖面质量。在图10(a)显示了原始炮集记录的地震剖面，其横向坐标范围为14～40 km，旅行时范围为500～6 000 ms。由于多次波速度与一次波的速度存在较大差异，经过偏移成像处理后，多次波信号受到了明显压制。但是，该剖面中仍然存在连续的多次波同相轴(例如箭头指向的位置)，同时，由于多次波信号的存在，导致该剖面中部位置信噪比较低，一次波同相轴的连续性较差。图10(b)显示了经多次波压制后的叠前时间偏移剖面，多次波同相轴得到了较好压制(例如箭头指向的位置)，所示剖面中部一次波同相轴连续性明显变好，其所描述的地质构造愈加清晰。

4 结论

论文在系统分析海底多次波的形成机制及传播规律的基础上，提出了基于多次反射界面等效模型进行射线追踪的三维多次波预测与压制方法。该方法经过理论模型检验和实际资料的处理结果验证了其有效性，并得出如下结论：

(1)基于多次反射界面等效模型进行射线追踪的三维多次波预测与压制方法，不仅有效回避了三维共面元道集覆盖次数(道数)空间分布不均匀的问题，而且还解决了由于动校正过程导致的地震信号畸变现象，显著提高了在三维炮集域内对多次波的压制效果，极大地提升了三维多次波衰减的计算效率。

(2)在三维地震勘探中，由于三维空间中的多次波传播路径复杂，其追踪难度和计算量都加大。通过使用本文的方法，建立多次反射等效界面，将多次波的传播路径转化为在等效反射界面上的一次反射路径，可降低基于射线追踪方法求取多次波旅行时的难度，从而可实现复杂构造区域海底多次波的精确追踪与剔除。

本文方法主要针对海底多次波，结合更为先进的速度建模技术，精确获取海底之下强反射界面的速度模型，从而实现海底之下强反射界面的多次波预测与剔除将是下一步的研究工作。