大型半潜浮式风机平台设计及稳性研究❋
宋兆波, 施 伟,2❋❋, 张礼贤, 里 程, 李 昕,2, 王 滨
(1.大连理工大学建设工程学部, 辽宁 大连 116024; 2.大连理工大学海岸和近海工程国家重点实验室, 辽宁 大连 116024;3.大连交通大学机械工程学院, 辽宁 大连 116028; 4.浙江省深远海风电技术研究重点实验室, 浙江 杭州 311122)
近年来,全球海上风电的研究和工程实践发展迅速,单机容量不断增大,在提高发电效益的同时因风机重量和叶片尺寸的增大也提高了对基础的要求[1];此外,水深不断增加,在水深大于50 m的海域,浮式基础相较固定式基础更具经济性优势,是深远海风能开发的必然选择,但中国漂浮式风电的研究起步相对较晚,目前常用的海上风机基础仍是单桩基础[2],而设计过渡水深(50 m水深左右)下的大型浮式风机平台顺应中国未来深远海风能开发的需要,具有现实意义。
根据获得静稳性的原理,可将现有的浮式风机平台分为半潜式、Spar式和张力腿式平台。与另外两种类型相比,半潜式平台适用水深范围更广,施工和安装更加方便[3]。近年来,学者们针对半潜浮式风机开展了大量的研究。Roddier等[4]提出利用侧柱支撑风机的WindFloat平台;多数半潜浮式平台由中柱支撑上部风机,欧盟LIFES50+项目提出了OO-star钢筋混凝土平台[5],邓露等[6]提出了一种钢筋混凝土半潜浮式风机平台,Zhang等[7]进行了OC4-DeepCwind、Braceless和V形半潜平台的对比研究,上述平台的立柱都是垂直的,Cao等[3]还提出了侧柱部分倾斜的浮式平台概念。
与传统海洋平台不同,风机平台运行时风轮叶片承受巨大的风载荷,而且风机平台的高耸塔架结构,使得风机平台承受更大的风倾力矩,而稳性是平台在外力作用下倾斜,外力消失后自行恢复到原平衡位置的能力[8],是评价漂浮式风机平台设计是否合理的重要因素。稳性包括完整稳性和破舱稳性,完整稳性又包括初稳性和大倾角稳性,二者的评价指标分别是初稳性高和风倾力矩与回复力矩曲线图(以下简称力矩曲线图)[9]。此前,张亮等[10]对其设计的5 MW半潜风机平台使用SESAM进行了完整和破舱工况下的稳性分析;郝红彬等[11]设计了桁架式气垫驳船平台,通过多气垫和增加气垫侧壁厚度来提高平台稳性;章李卉[12]对复合筒型基础的拖航稳性进行研究,并采用MOSES软件对复合筒型基础进行了优化分舱稳性计算;Islam[13]将WindFloat平台扩尺支撑DTU 10 MW风机,并基于静平衡角对平台的尺寸进行优化。
基于目前国内外研究成果,考虑钢筋混凝土结构成本低、耐腐蚀和施工简便的优势,本文基于DTU 10 MW风机提出了一种倾斜立柱式半潜平台设计方案,采用SESAM对新型平台进行数值模拟,探究立柱间距、倾角、直径等对半潜浮式平台稳性的影响规律,以期为半潜浮式平台的稳性设计提供有力的参考。
1 半潜平台设计方案
本文针对中国广东省某海域,开展支撑10 MW级大型风机的半潜平台设计,设计水深为50 m。此新型半潜平台三个侧柱呈等边三角形布置,侧柱向外倾斜,中柱位于三角形的中心,立柱之间通过底部浮筒连接,风机位于中柱上,使用法兰连接。平台和内部隔板均为钢筋混凝土结构,密度取2 500 kg/m3。图1为半潜风机平台示意图和参考坐标系,原点在自由水面,Z轴向上。对于波浪和风荷载,0度表示沿X轴正方向。DTU 10 MW风机[14]参数如表1所示。

图1 半潜平台概念设计图

表1 DTU 10 MW风机参数
半潜浮式风机主要依靠水线面的惯性矩获得足够的稳性来抵抗风载荷引起的倾覆力矩。其中,Braceless半潜浮式平台[15]将立柱间距增加到45 m,以获得足够的稳性,然而增大间距会使立柱之间的浮筒长度增加,导致应力增大和结构疲劳;OO-Star平台[5]通过扩大立柱直径来增加水线面的惯性矩,这将直接导致水线面和排水量增加;Triple-Spar平台[16]将三根立柱的高度增加到65 m来满足稳性要求,导致成本的急剧增加。
综合考虑现有的5 MW浮式风机平台结构,确定初步的平台尺寸,调整立柱间距、立柱倾角及立柱直径等参数,分析不同参数对平台稳性的影响,得到半潜平台的最终尺寸(见表2)。
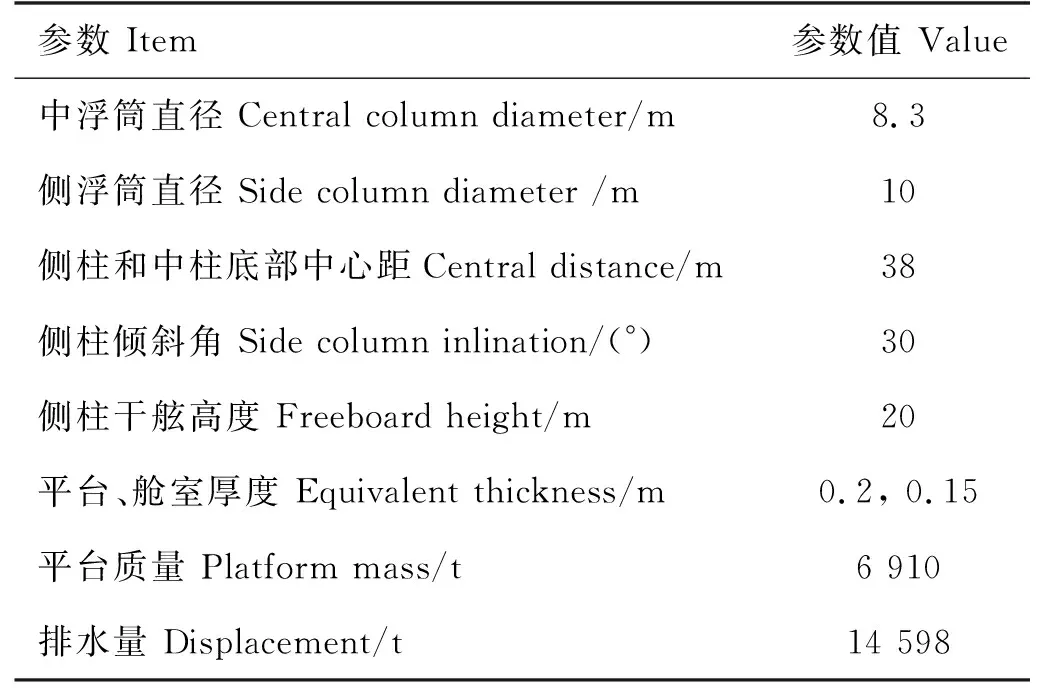
表2 半潜风机平台参数
2 稳性分析
2.1 SESAM稳性计算
SESAM是一款强大的海洋工程领域的结构设计分析软件。本文采用SESAM进行稳性计算与分析,使用SESAM中的GeniE模块和HydroD稳性分析模块进行稳性计算与分析,计算流程如下:
(1)在GeniE中完成建模和网格划分,图2为平台的湿表面模型和结构模型,结构模型中包括结构的质量参数和分舱信息。

图2 半潜平台有限元模型
(2)将以上的文件导入HydroD Stability,并输入舱室的渗透率、舱室压载的百分比、风廓线等计算稳性的参数,进行平台的完整稳性分析。
(3)将完整稳性分析中的舱室设置flooded,若舱室位于水下,则舱室破损后满载,若舱室位于水面线位置,则舱室内液面始终与自由水面一致,根据舱室破损后的质量模型得出新的浮态,包括自由水面、横倾和纵倾角,进行平台的破舱稳性分析。
(4)选取平台完整稳性和破舱稳性的计算结果和规范,计算两个工况下的许用重心高度,得出综合许用高度。
考虑湍流等因素,10 MW风机轮毂处11.4 m/s对应的最大推力取额定推力的1.25倍[13],由公式(1)[13]计算得出风轮叶片等效圆盘的直径,保证推力和平台的风倾力矩与实际相一致,塔筒风载荷和风倾力矩同样按照公式(1)进行计算。

(1)
式中:CS为形状系数;CH为高度系数,可参考规范DNVGL-OS-C301[17];ρa为空气密度;A为迎风面积;V为风速;H为风载荷作用中心到平台浮心的竖向距离。
2.2 完整稳性分析
由船舶初稳性理论可知,当船舶小角度(10°~15°) 倾斜时,假定等体积倾斜,水线面的交线通过原水面线的形心(也称漂心)[8],平台的初稳性高和回复力矩分别根据公式(2)和(3)进行计算[13]:
(2)
(3)

浮式风机处于复杂的海洋环境之中,所受风载荷的大小和方向一直发生变化,浮式风机平台向不同方向倾斜时,稳性有所差异,所以存在最不利的倾斜轴,平台对应该倾斜轴的稳性最低。根据已知结论,不论风向如何,平台必绕着垂直风向的倾斜轴倾覆,进水角最小时对应的轴线就是最不利倾斜轴[9],本文中半潜平台的风向角如图1所示,0°风向角对应平台进水角最小,平台稳性也最不利。
初选浮式平台立柱间距为43 m,根据船舶静力学[8],当浮体倾斜时,重力和浮力不再作用于同一铅垂线上,自重心作垂直于浮力作用线的直线即回复力臂,回复力矩仅与重心和浮心的位置相关,所以平台在运行工况和自存工况下对应每一个倾斜角的回复力矩相同,且根据式(1)计算,运行工况下的最大风倾力矩为251.1 MN·m,自存工况下(风速25 m/s)的最大风倾力矩为120.8 MN·m,半潜平台的自存工况的稳性高于运行工况,因此,本文仅针对运行工况下0°风向角对应的半潜浮式平台稳性进行分析。
本文以立柱间距、倾角及直径为变量,采用SESAM进行数值模拟,探究对最不利倾斜轴对应的平台稳性的影响规律,并对平台尺寸进行优化。
2.2.1 立柱间距对平台完整稳性的影响 依次减小立柱间距,其他参数不变,探究立柱间距对稳性影响规律的同时,减小平台的尺寸使其达到满足稳性衡准的最小尺寸,计算结果如表3所示。

表3 不同立柱间距的完整稳性
图3为不同立柱间距的平台对应的力矩曲线和初稳性高随立柱间距的增长量,L表示立柱间距。由表3和图3(a)可知,随着立柱间距的减小,静平衡角变大,面积比和初稳性高均减小,平台稳性降低。这是因为减小立柱间距,水线面惯性矩的变化率高于排水量,同时重心和浮心竖向距离的增大,使得平台初稳性高和面积比减小,初稳性高随立柱间距的增长量如图3(b)所示,ΔGM1表示稳性增长量中重心和浮心垂直距离影响的部分,ΔGM2表示稳性增长量中水线面惯性矩和排水体积影响的部分,可知增大间距平台稳性主要受水线面惯性矩和排水体积的影响,重心和浮心垂直距离的减小对平台初稳性高增大的贡献仅20%左右。
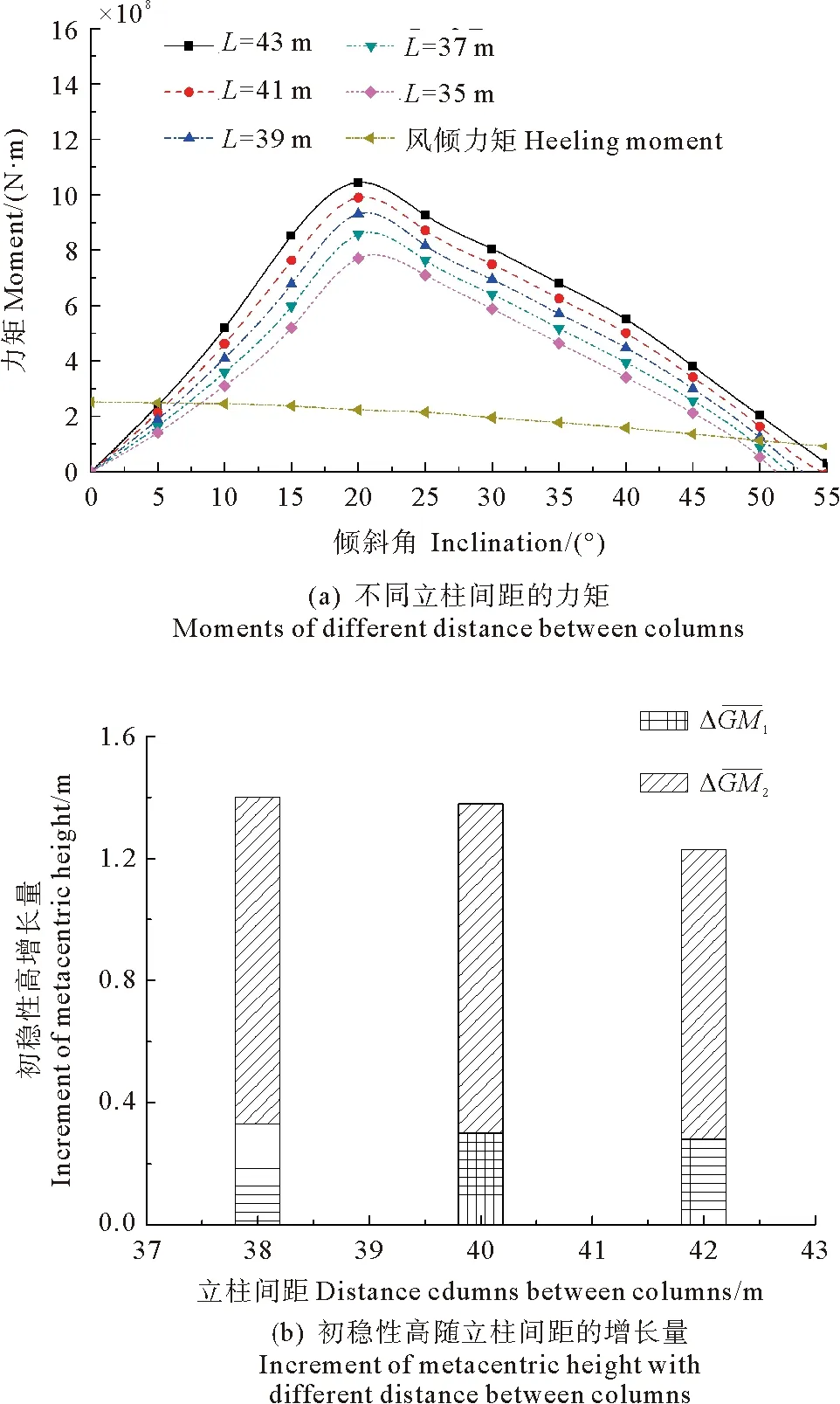
图3 不同立柱间距的平台完整稳性
根据IMO规范[18],从初始平衡位置到进水角之间回复力矩和风倾力矩曲线下的面积比大于1.3,所以立柱间距调整为37 m。
2.2.2 立柱倾角对平台完整稳性的影响 以立柱间距为37 m的概念平台为基础,作为模型1,构建模型2和3,探究立柱倾角对平台稳性的影响,模型1、2和3的唯一区别在于立柱倾角,依次为30°、35°和40°,稳性计算结果如表4所示。

表4 不同立柱倾角的完整稳性
图4为不同立柱倾角的平台对应的力矩曲线和初稳性高随立柱间距的增长量。由表4和图4(a)可知,随着立柱倾角的增大,平台稳性增强,由图4(b)可知,平台初稳性高增大主要因为水线面惯性矩和排水体积比值增大,浮心和重心位置的变化对稳性增加的贡献10%。

图4 不同立柱倾角的平台完整稳性
2.2.3 立柱直径对平台完整稳性的影响 构建模型4和5,模型1、模型4和模型5的唯一区别在于侧柱直径,依次为10、10.5和11 m,探究立柱直径对平台稳性的影响,稳性计算结果如表5所示。为便于平台底部浮筒和侧柱的连接,研究中浮筒宽度和侧柱直径始终相等。

表5 不同立柱直径的完整稳性
图5为不同立柱直径的平台对应的力矩曲线和初稳性高随立柱间距的增长量。由表5和图5(a)可知,随着立柱直径的增大,平台稳性增强。由图5(b)可知,增大立柱直径,水线面惯性矩与排水体积比值和浮心与重心位置对平台的稳性都有着很大影响,立柱直径由10 m增加到10.5 m,稳性主要受浮心和重心位置的影响,立柱直径大于10.5 m,稳性主要受水线面惯性矩与排水体积比值的影响。增大浮筒直径能显著提高浮式风力机平台的稳性,但是,增大立柱直径会增大舱室的容积,同样的分舱条件下,破舱稳性会更加不利。

图5 不同立柱直径的平台完整稳性
图6为平台的质量和排水体积随面积比和初稳性高的增长相对于模型1的增长率,实线代表平台质量增长率,虚线代表平台排水体积增长率。可以看出,通过增大立柱间距、倾角和直径三种方式增长相同的面积比和初稳性高,增大立柱倾角对应的平台质量和排水体积的增长率最小,其次为增大立柱间距,而通过增大立柱直径增长面积比对应的平台质量和排水体积的增长率最大。

图6 平台参数随面积比的增长率
平台通过增加立柱倾角,相比增大立柱间距和直径,同样的稳性需要的排水量更小,平台钢筋混凝土用量更低,证明倾斜立柱式的半潜浮式风机平台在稳性方面更具优势,所以提高平台稳性首先调整立柱倾角,其次为立柱间距,最后是立柱直径。但是过大的立柱倾角会引起明显的波浪爬高,同时对立柱和底部浮筒连接处的应力不利,由于缺乏相关的研究,为安全起见,立柱倾角不大于30°。
2.3 破舱稳性分析
破舱稳性主要研究浮式平台舱室破损而进水后,风机不会倾覆或沉没,仍具备一定稳性的能力。平台的破舱稳性与舱室划分有着很大关系,舱室划分过少,某一舱室破损进水体积过大将导致平台失稳倾覆; 舱室划分过多,会增加浮式平台的材料用量,降低经济性,因此对稳性起重要作用的舱室高度尺寸要尽量均匀,且舱室高度不宜偏高,压载水在舱室内的分布应使得重心尽量低来增加稳性高度,获得比较大的稳性。综合考虑破舱稳性要求、舱室布置优化及经济性,底部浮筒满载,不设置分舱,水线附近的舱室的破损对整个平台的影响最大,浮式风机平台舱室划分如图7所示,中柱高30 m,自上而下设置3个高4 m的舱室、3个6 m 舱,侧柱垂直高度为40 m,自上而下设置3个6 m舱,1个4 m舱、3个6 m舱作为分舱1,调整侧柱水线面以下的舱室高度为4.5、3.6 m作为分舱2和3,内部隔板厚度为150 mm。

图7 舱室划分示意图
针对破舱稳性,借鉴海工平台设计经验,根据浮式风机破损的成本效益分析,10 MW以内的浮式风机破舱稳性只计算单舱破损[19],所以对于基于DTU 10 MW风机的概念平台只计算单舱破损后的破舱稳性。水线面附近的舱室更易破损,背风向侧柱上的舱室破损,重心右移会导致平台产生与风倾力矩方向一致的倾斜,且水下舱室容积相同,上部舱室距离中心线最远,破损对稳性最不利,所以分析舱室Cm_LC13(即图7中水线面附近舱室)运行工况下破损后的平台稳性,平台破舱稳性计算结果如图8所示。

图8 舱室Cm_LC13破损力矩曲线图
结合IMO MODU规范[18],由图8可知,分舱1的舱室破损后从第一交点至风雨密角度范围为5.65°,分舱2的舱室破损后从第一交点至风雨密角度范围为6.75°,均小于7°,不满足破舱稳性规范要求;分舱模型3,舱室破损后平台静倾角10.50°,从第一交点到风雨密角度范围7.39°,且在这一范围内,16°倾斜角对应复原力矩514.83 MN·m,风倾力矩234.99 MN·m,比值大于2,分舱模型3满足破舱稳性的要求,而舱室细分对平台的完整稳性几乎没有影响,可以忽略。
2.4 综合许用重心高度
许用重心高度是指平台能满足稳性衡准的最大重心高度,浮式平台在各工况下其重心高度不得超过此极限值,否则会造成稳性不足[19]。本文只计算了浮式风机平台运行工况在完整和破损状态下的许用重心高度,其中许用重心高度的较小值即为平台的综合许用重心高度。经稳性计算校核舱室调整后的平台的重心高度和许用重心高度的关系,结果如表6所示。

表6 立柱间距对平台许用重心高度的影响
将立柱间距由37 m增加至38 m,半潜平台满足许用重心高度要求,立柱间距增大浮式平台自然满足完整稳性的要求,同时破舱稳性的静平衡角和进水角都在减小,经计算,从第一交点到风雨密角度范围7.62°,破舱稳性仍满足规范要求。
2.5 固有周期
浮式平台需要足够的稳性,但是其稳性不宜过大,平台稳性越大,固有周期越短,从而接近波浪周期而引起共振。一般来说,波浪的周期范围在5~15 s左右,半潜式平台的设计要求垂荡、纵摇和横摇的固有周期大于20 s,平台非耦合纵摇和横摇周期可根据公式(4)进行初步计算[20]:
(4)
式中:Tni为浮式平台纵摇和横摇的固有周期;M为浮式风机平台质量;rii为浮式风机绕通过重心且平行于倾斜轴线的惯性半径;Aii为附加惯量矩,i=4,5。可以看出,平台纵摇和横摇周期随着初稳性高的增大而变短。
垂荡方向的固有周期可根据公式(5)[20]得出:
(5)
式中:Tn3为浮式平台垂荡的固有周期;A33为附加质量;Aw为水线面面积。优化后的半潜平台破舱稳性和许用重心高度均满足规范要求,完整稳性和固有周期如表7所示,垂荡、纵摇以及横摇的固有周期远离波浪频率主要范围。

表7 最终平台的完整稳性和固有周期
3 结论
本文提出了基于DTU 10MW风机的大型钢筋混凝土半潜浮式风机平台的概念设计方案,分析了立柱间距、倾角和直径等因素对浮式平台稳性的变化规律并对平台尺寸进行了优化,得到以下结论:
(1)立柱间距和立柱倾角主要通过改变水线面惯性矩与排水体积比值来影响稳性,而改变立柱直径,水线面惯性矩与排水体积比值以及重心与浮心的垂直距离都对稳性有很大影响。
(2)初稳性高与立柱直径近似线性关系,且随着立柱直径的增大,重心与浮心的垂直距离对初稳性高的影响降低。
(3)通过增大立柱间距、倾角和直径三种方式增长相同的面积比和初稳性高,增大立柱倾角对应的平台质量和排水体积的增长率最小,此外增加立柱间距比增加立柱直径经济性好,可根据实际情况选用最优的措施调整浮式风机平台的稳性。
基于本文工作,未来将进一步开展平台强度和疲劳分析。此外,对于浮式风机平台的拖航工况进行稳性方面的分析,从而对平台作进一步优化。

