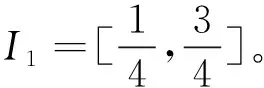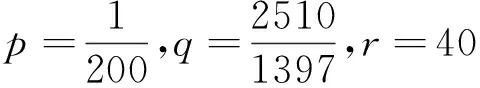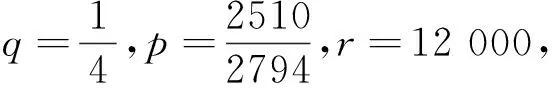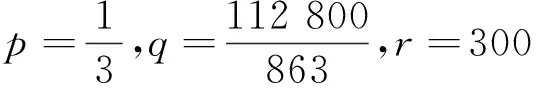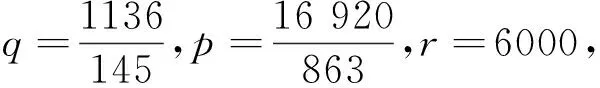一类四阶微分方程Neumann边值问题的多正解性
徐 晶,高红亮
(兰州交通大学 数理学院,甘肃 兰州 730070)
常微分方程边值问题是微分方程理论研究中的一个重要问题,在弹性力学和工程物理等领域中应用广泛,对其正解研究受到许多学者关注[1-10]。
2008年,Li[1]等运用不动点指数理论和临界群研究了四阶微分方程边值问题
(1)
解的存在性,其中f∈C([0,1]×R,R)且对任意的x∈[0,1],f(x,·)在R上单调递增。2009年,郭建敏等[3]运用Morse理论和Brezis-Nirenberg理论研究了四阶微分方程边值问题
(2)
2015年,Vrabel[5]运用上下解方法研究了两端简单支撑的静态梁方程边值问题
(3)
解的存在性,其中参数k1 (4) 引理1[8]设P是实Banach空间B中的锥,若映射α:P→[0,+∞)是连续的且 α(tx+(1-t)x)≥(≤)tα(x)+(1-t)α(x),x,y∈P,t∈[0,1], 则称映射α是凹(凸)泛函。 令β,γ和θ是锥P上的非负连续凸泛函,α和Ψ是锥P上的非负连续凹泛函,对于非负实数d,p和q,定义集合: P(γ,r)={y∈P|γ(y) Q(γ,β,d,r)={y∈P|β(y)≤d,γ(y)≤r},P(γ,θ,α,p,q,r)={y∈P|α(y)≥p,θ(y)≤q,γ(y)≤r}。 引理2[8]设P是实Banach空间B中的锥,α,γ是锥P上的非负连续增泛函,θ是锥P上的非负连续泛函且满足θ(0)=0。对于任意正数r,存在正数M,使得 假设存在正数p,q满足p θ(λy)≤λθ(y),λ∈[0,1],y∈∂P(θ,q)。 (ⅰ)α(Ty)>r,y∈∂P(α,r); (ⅱ)θ(Ty) (ⅲ)P(γ,p)≠∅且γ(Ty)>p,y∈∂P(γ,p)。 γ(y1)>p,θ(y1) 引理3[8]设P是实Banach空间B中的锥,r和M是正数。假设α,Ψ是锥P上的非负连续凹函数,γ,β和θ是锥P上的非负连续凸泛函且满足 (ⅰ) {y∈P(γ,θ,α,p,q,r)|α(y)>p}≠∅且α(Ty)>p,y∈P(γ,θ,α,p,q,r); (ⅱ) {y∈P(γ,β,Ψ,h,q,r)|β(y) (ⅲ)α(Ty)>p,y∈P(γ,α,p,r)且θ(Ty)>q; (ⅳ)β(Ty) 本文假设f:[0,1]×[0,+∞)→[0,∞)是连续函数。 其中 容易验证Gi(x,s)有如下性质: (ⅰ)Gi(x,s)>0,x,s∈[0,1]; (ⅱ)k1i(x)Gi(s,s)≤Gi(x,s)≤Gi(s,s),x,s∈[0,1],其中 P={y∈C[0,1]|y(x)≥0,y(x)≥k11(x)δ2m2‖y‖}, 定义算子T:P→P为 定理1假设存在常数p,q,r满足0 则问题(4)至少存在两个正解y1,y2,满足 证明令 易知α,γ是P中的非负连续增泛函,θ是P上的非负连续泛函且θ(0)=0,ni≥mi。对任意y∈P,可知 易证T:P→P为全连续算子。下证引理2中的条件(ⅰ)~(ⅲ)成立。 首先,对任意y∈∂P(α,r),有 θ(y)=q≥α(y)≥δ1δ2n1m2γ(y), 最后,可知 P(γ,p)={y∈P|‖y‖ 且对任意y∈∂P(γ,p),即‖y‖=p,有α(y)≥δ1δ2n1m2p,根据条件(ⅲ)可得 综上,由引理2可知,问题(4)至少存在两个正解y1,y2,满足 则问题(4)至少存在三个正解y1,y2,y3满足不等式 证明令 易知α,Ψ是P中的非负连续凹泛函,γ,β,θ是P中的非负连续凸泛函,ni≥mi。 取y=δ1δ2n1m2q,显然y∈P(γ,β,Ψ,δ1δ2n1m2q,q,r)。因为β(y)=δ1δ2n1m2q {y∈P(γ,β,Ψ,δ1δ2n1m2q,q,r)|β(y) 对任意y∈P(γ,β,Ψ,δ1δ2n1m2q,q,r),根据条件(ⅱ)可得 令y∈Q(γ,β,q,r)使得Ψ(Ty)<δ1δ2n1m2q,则 综上,由引理3可知,问题(4)至少存在三个正解y1,y2,y3满足 例1考虑四阶微分方程Neumann问题 正解的存在性,其中w1=2,w2=1,k1 (1)若非线性项f的形式为 综上,在此条件下,边值问题至少有两个正解y1,y2满足 (2)若非线性项f的形式为 综上,在此条件下,边值问题至少有三个正解y1,y2,y3满足 例2考虑四阶微分方程Neumann问题 (1)若非线性项f的形式为 综上,在此条件下,边值问题至少有两个正解y1,y2满足 (2)若非线性项f的形式为 综上,在此条件下,边值问题至少有三个正解y1,y2,y3满足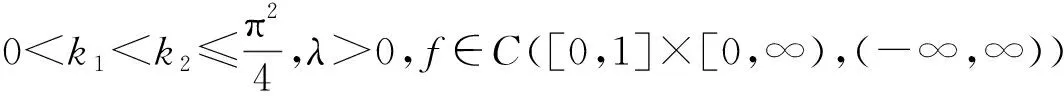
1 预备知识
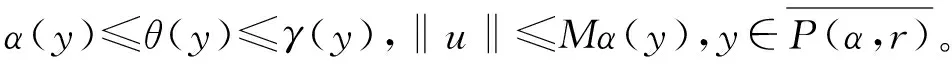
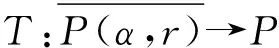
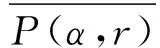
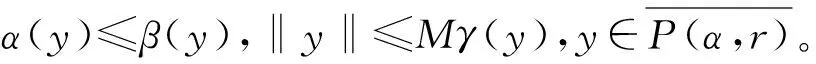
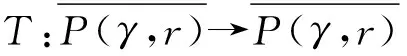
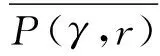
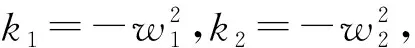
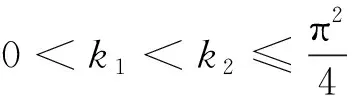
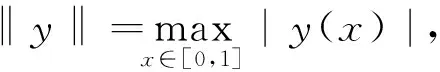
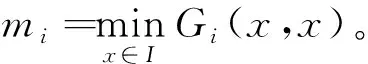
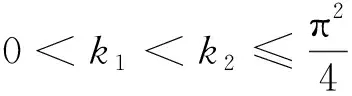
2 主要结果
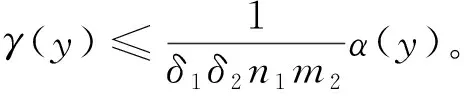
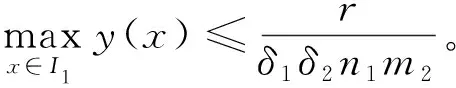
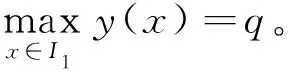
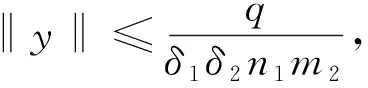
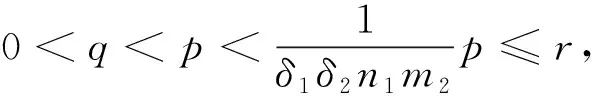
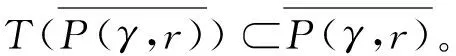
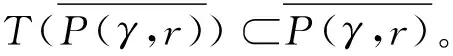
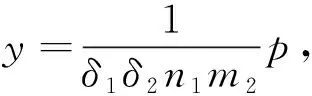
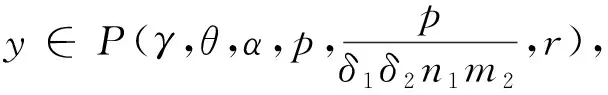
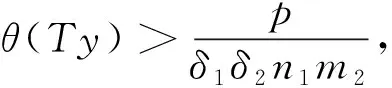
3 主要应用