一类具有饱和发生率的时滞传染病模型稳定性

刘 娟，陈 功

(蚌埠学院 理学院，安徽 蚌埠 233030)

近年来，为了预防和控制传染病的传播，许多传染病模型相继被国内外学者提出。在传染病模型构建中，发生率起着至关重要的作用。因此，为了合理分析、研究传染病的传播机理，必须选取恰当的发生率。在许多传染病模型中都是采用了双线性发生率[1-4]。但是，双线性发生率假设染病者的数量是按线性增长的，这种假设对于某些传染病而言无法全面描述其传染规律。相对而言，非线性发生率更能准确地描述传染病的发生规律[5-9]，在各种类型的非线性发生率中，饱和发生率是具有代表性的一种，文献[7]讨论了具有饱和发生率的SEIR模型：

(1)

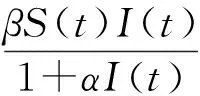
然而，在模型(1)中并未考虑到疾病传播过程中所存在的时滞因素，尤其是疾病的潜伏期时滞。而时滞因素对一个动力系统的动力学性质有着非常重要的影响，比如，可以引起系统稳定性的变化，导致Hopf分支和周期解的发生。基于此，本文在模型(1)中引入疾病的潜伏期时滞，得到下列具有时滞的SEIR传染病模型，主要研究时滞传染病模型的渐近稳定性和平衡点外围出现Hopf分支的充分条件。

(2)

其中，τ是疾病的潜伏期时滞。

1 模型的局部稳定性和Hopf分支的存在性

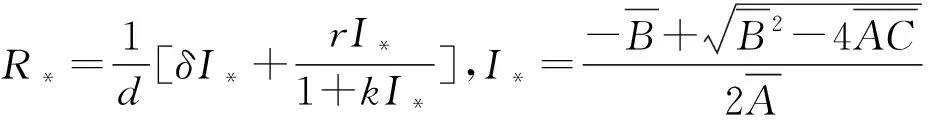
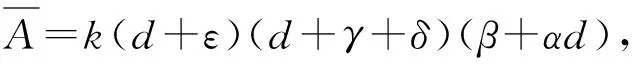
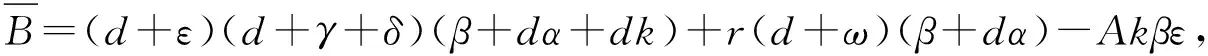
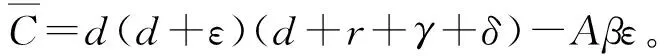
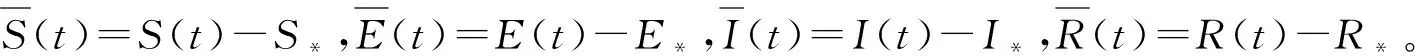
(3)

其中

f1=a14S(t)I(t)+a15I2(t)+a16S(t)I2(t)+a17I3(t)+…,

f2=a25S(t)I(t)+a26I2(t)+a27S(t)I2(t)+a28I3(t)+…,

f3=a34I2(t)+a35I3(t)+…,

f4=a45I2(t)+a46I3(t)+…,

进而得到系统(3)的线性化部分为

相应特征方程为

λ4+m3λ3+m2λ2+m1λ+m0+(n3λ3+n2λ2+n1λ+n0)e-λτ=0,

(4)

其中

m0=(a11a22-a12a21)a33a44,m1=-[a11a22(a33+a44)+(a11+a22)a33a44],

m2=a11a22+a33a44+(a11+a22)(a33+a44),m3=-(a11+a22+a33+a44),

n0=a44(a11a33b22+a13a21b32),n1=a23b32(a11+a44)-(a11a33+a11a44+a33a44)b22-a13a21b32,

n2=(a11+a33+a44)b22-a23b32,n3=-b22。

当τ=0时，方程(4)变为λ4+A3λ3+A2λ2+A1λ+A0=0,其中

A0=m0+n0,A1=m1+n1,A2=m2+n2,

令Det1=A3,那么，根据Routh-Hurwithz稳定性判据，则

成立，这说明正平衡点P*(S*,E*,I*,R*)是局部渐近稳定的。

在τ>0的前提下，设λ=iω(ω>0)为特征方程(4)的根，则可得到

(5)

从而得到

ω8+e3ω6+e2ω4+e1ω2+e0=0。

(6)

其中

令ω2=v，则方程(6) 变为

v4+e3v3+e2v2+e1v+e0=0。

(7)

文献[10]研究了上述方程根的分布情况，基于此提出如下假设:

(H1)方程(7)至少有一个正根。

其中

h0=-m0n0,h2=m0n2-m1n1+m2n0,h4=m1n3-m2n2+m3n1-n0,h6=n2-m3n3。

将λ(τ)代入方程(4)，并对方程(4)求λ关于τ的导数，则有

进而有

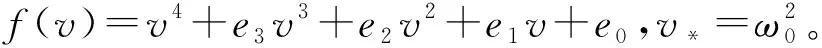
定理1若(H1)成立，则当τ∈[0,τ0)时，传染病模型(2)的正平衡点P*(S*,E*,I*,R*)是局部渐近稳定的；当τ=τ0时，平衡点P*(S*,E*,I*,R*)外围出现Hopf分支。

2 模拟仿真

对模型进行仿真，在模型的参数中，令A=15,d=0.5,k=2,r=0.2,α=0.8,β=0.3,γ=0.2,δ=0.4,ε=1.2,则可以得到系统(2)的一个示例

(8)

经过计算可以得到R0=4.8869>1，进而得到系统(8)的唯一正平衡点P*(194224,3.1112,3.3150,2.8258)。容易验证，条件(H1)成立，并得到ω0=1.2707和τ0=2.5898。仿真效果如图1、图2所示。

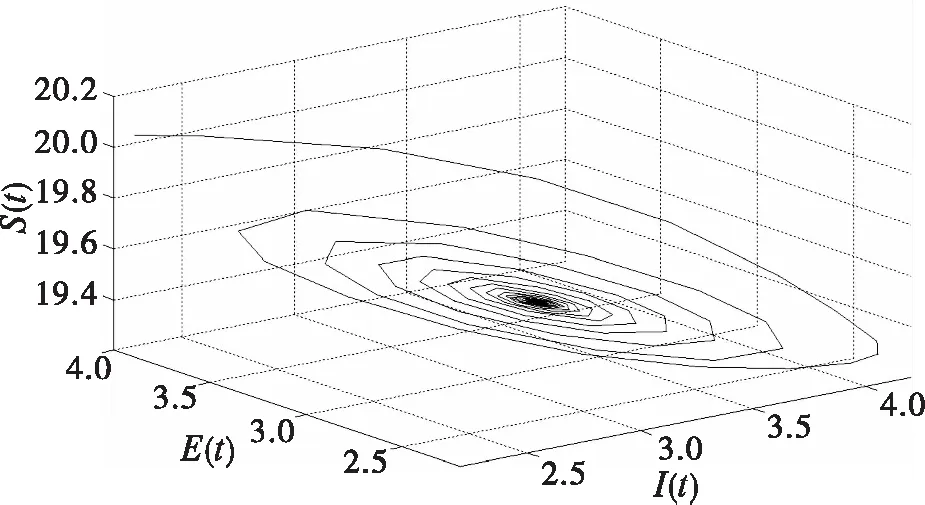
图1 当τ=2.35<τ0时，P*渐近稳定

图2 当τ=3.15>τ0时，P*失去稳定性并产生Hopf分支

3 小结

本文在文献[7]中所提出的SEIR传染病模型的基础上，研究了一类具有饱和发生率和饱和治愈率的时滞SEIR传染病模型的局部稳定性和Hopf分支问题。相对于文献[7]中的所研究的模型，本文进一步考虑了疾病的潜伏期时滞。因此，本文所研究的模型更具有一般性,所得理论分析结果是对文献[7]的补充。但是，本文只是研究了模型正平衡点的局部稳定性，并没有对模型正平衡点的全局稳定性进行讨论。所以，下一步笔者将试图通过构造合适的李雅普诺夫函数对模型(2)的全局稳定性进行研究，并研究模型的Hopf分支方向、稳定性以及周期解的周期大小等性质。