基于改进序贯均匀设计的常微分方程组参数估计
王福昌,贺财宝
(防灾科技学院 基础部,河北 廊坊 065201)
0 引言
均匀设计是我国数学家方开泰和王元提出的一种试验设计方法,特别适用于多水平多因素的试验设计复杂情形,主要通过均匀设计表进行试验设计[1]。该方法自1978年被提出以来,引起了数学和统计学专家广泛的关注[1-6]。
常微分方程组是一种应用广泛的数学模型,它的参数一般通过专家的专业知识确定。研究者一般假定模型参数已知时,讨论方程的性质,对于其反问题的研究相对较少。在实际应用中,要想根据试验观测数据筛选合适的模型,对它的参数进行精确估计变得十分重要,有一些文献对这一问题开展了研究[7-10]。针对最常见的猎物-捕食者模型的参数估计,人们提出了最小二乘逼近(LSA)法[7]、函数型数据分析法[8]和混合加速粒子群算法[9]。对于传染病SIR模型,一般在最小二乘法准则下用单点迭代法[10]。
以上传统的迭代方法,有的对初值依赖,有的过于复杂,本文先把参数估计问题化为多变量优化问题,再用并行和精英保留策略改进序贯均匀设计来估计微分方程组的参数,最后通过三个典型的应用案例检验方法的正确性和有效性。
1 基本假设和模型
假定常微分方程初值问题模型为
(1)
其中,y(t)=[y1(t),y2(t),…,yp(t)]T为关于时间的待求函数向量,θ∈Rs为模型参数,F(t,y(t),θ)为确定的非线性向量函数。再假设当给定初值条件y(t0)=y0后,方程(1)存在唯一精确解。
设在时刻t1,t2,…,tn处y(t)的观测向量值为y(t1),y(t2),…,y(tn),预测向量值为h(t1,θ,y0),h(t2,θ,y0),…,h(tn,θ,y0)对应的最小二乘估计
(2)
通过优化模型(2),即可得到参数θ,y0的最小二乘估计。
最小一乘估计在遇到离群值时,稳健性更好,
也可给出M-估计形式[11]
ρ(·)可以取为Huber函数
其中c为常数。
有时优化的目标函数是预先设定的,如在连续时间确定性最优控制问题中,优化目标是直接给出的,约束是一个常微分方程初值问题[12]
x′=f(x,u),x=x(t)=xi(初值)。
2 算法和应用案例
均匀设计可以在参数候选解集内均匀选点,利用较少的计算点来避免陷入局部最优[1]。使用均匀设计方法需要先确定均匀设计表,而均匀设计表可以从网上下载(http://www.math.hkbu.edu.hk/UniformDesign/)或根据数学原理编程自动生成[13]。
2.1 算法设计
设χ=[a,b]为Rs中一个超矩形,其中
a=[a1,a2,…,as],b=[b1,b2,…,bs],
即ai≤xi≤bi,i=1,2,…,s并设f(x)为χ上的连续函数,希望在试验区χ上找到x*,使得
则称M为函数f(x)在区域χ上的全局最优值,x*为χ上的全局最优点。
这是一个典型的优化问题,通过均匀设计来寻找全局最大点是一种可行的方法,其主要思路如下:给定试验区域χ上的一个设计
P={xk,k=1,2,…,n},
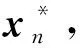
的一个设计点。可以证明,在前面假设下,当n→∞时,Mn→M,但这种方法的收敛速度还是很慢。Fang等提出的序贯均匀设计(Sequential Uniform Design Optimization,SNTO)[14]方法可以提高收敛速度。
设
P0={yk,k=1,2,…,n}
为Cs=[0,1]上的设计,并设
xki=ai+(bi-ai)yki,i=1,2,…,s,xk=(xk1,…,xks),k=1,2,…,n,
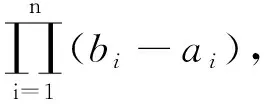
2.2 改进的序贯均匀设计方法
下面给出最小化目标函数的序贯均匀设计算法。
步骤1 初始化。设t=0,χ(0)=χ,a(0)=a,b(0)=b。
步骤2 产生均匀设计。在试验区域χ(t)=[a(t),b(t)]寻找一个试验次数为nt的均匀设计P(t),可以从网站下载,或者编写程序自动生成[13]。
步骤3 并行计算目标函数新的近似值。由于每个点并没有先后关系,因而可以用计算机的多个核同时计算目标函数值。选取每个均匀设计点x(t)∈P(t)∪{x(t-1)},使得
Mt=f(x(t))≤f(y),∀y∈P(t)∪{x(t-1)},
式中,x(-1)表示空集,x(t)和Mt分别为x*和f(x*)的近似值。
步骤4 终止准则。 令c(t)=(b(t)-a(t))/2,若maxc(t)<δ,其中δ为事先设定的很小的数,则χ(t)足够小,且x(t)和Mt是可以接受的,此时终止算法,否则转步骤5。
步骤5 更新试验区域并保留上次迭代中的最优点。新的试验区域
χ(t+1)=[a(t+1),b(t+1)],
其中
式中,γ称为压缩比。本次迭代中得到的最优点进入下次迭代,称为精英保留策略。记t=t+1,转步骤2。
2.3 应用案例
例1 SIR模型参数估计。用英国传染病监测中心1978年发布的有关流感病人的统计数据来估计SIR模型的参数。该数据统计了两周内每天某一所男孩寄宿学校流感爆发和流行情况,总共有763个学生,从发生一个染病者开始统计染病学生的人数,总共统计了15天,每一天统计得到的染病人数分别为1、3、7、25、72、222、282、256、233、189、123、70、25、11、4[10]。由于该数据收集时间很短,学生没有因病死亡,即人口总数是常数,b=0,d=0,模型为
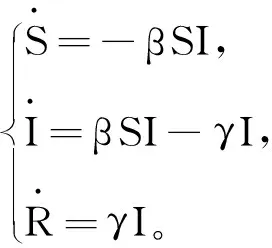
由假设,通过等价变形可以化为一个关于感染者的二阶微分方程模型
这里只有两个参数θ=(β,γ),可以通过可视化序贯均匀设计方法来直观了解参数寻优过程,见图1。根据文献信息,设置参数的初始搜索区间为β∈[0.001,0.003],γ=[0.4,0.5],即设a=[0.001,0.4],b=[0.003,0.5]。这里选用了100水平2因素的均匀设计表,均匀设计表通过Matlab自动生成[12]。压缩系数取为γ=0.9,误差取为10-6,后面采用同样设置通过多次尝试筛选,迭代出来的参数估计为θ*=(0.0021,0.4820),图1(a)表示预测值与观测值的残差平凡和对着迭代次数增加而变化的情况,图1(b)表示按照得到的参数估计结果绘制的拟合曲线与观测值的对比,可以看到估计出的参数符合观测结果。
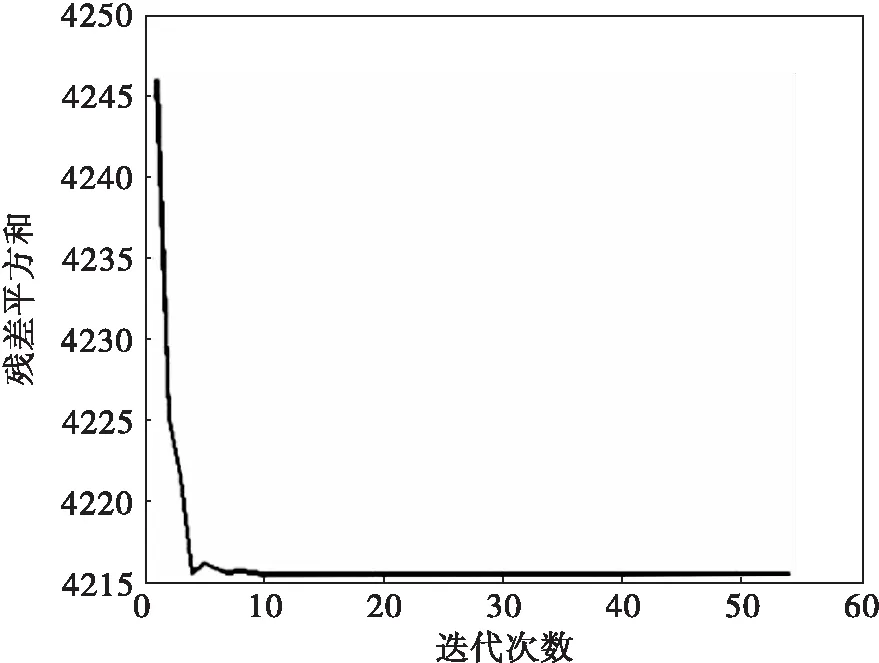
(a)残差平方和随着迭代次数变化
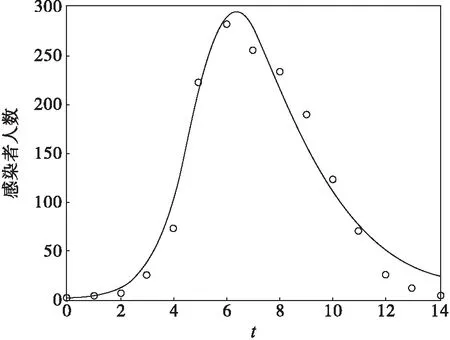
(b)感染者随时间变化分布与拟合曲线
注意观察可以发现,图1(a)的目标函数值一开始并没有随着迭代次数严格递减,这是因为为了避免早熟现象,即过早陷入局部极小值,在设计程序时,迭代的前5步没有采用精英保留策略。后面两个例采用了相同的前5步不用精英保留策略设置。
例2 酶积累问题(enzyme effusion problem)的数学模型可描述为[16]
其中
p=[p1,p2,p3,p4],y0=[y1(0),y2(0)]
为待估参数,观测数据见表1。
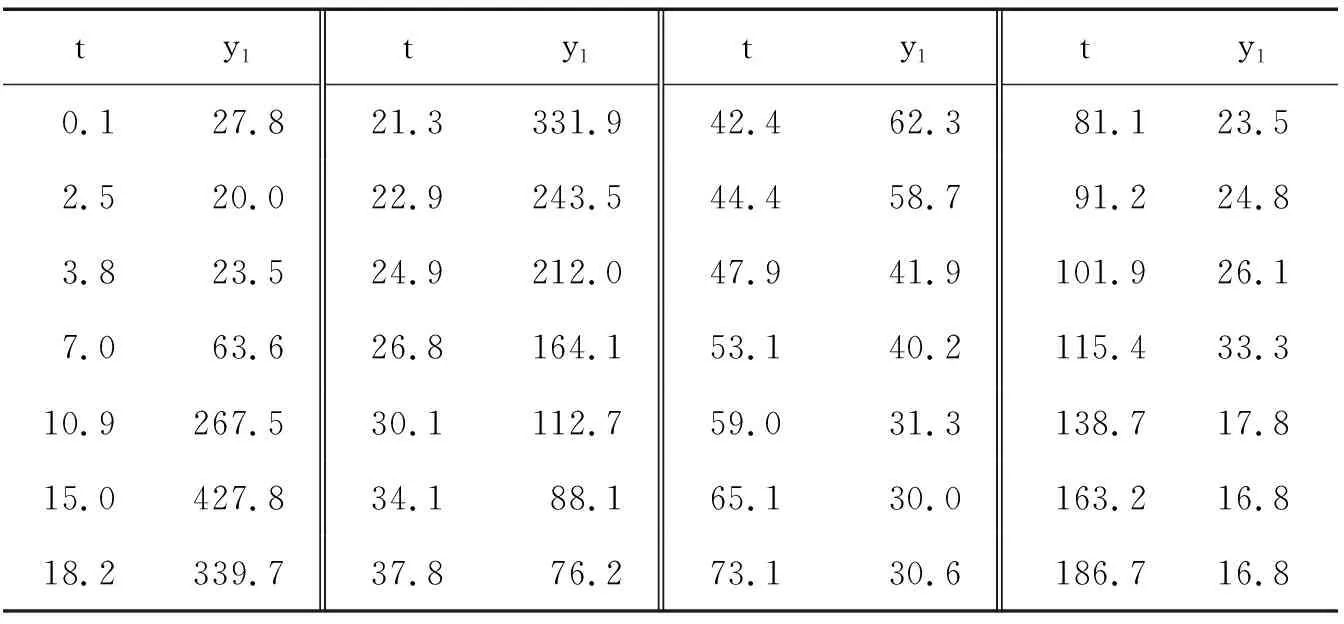
表1 酶积累问题的部分观测数据
根据表1数据和公式(2),可构造一个含6个自变量的目标函数,优化参数范围取为
0.1≤p1≤0.5,2.5≤p2≤3,0.3≤p3≤0.5,
0≤u4≤0.15,21≤y1(0)≤23,30≤y2(0)≤38。
这里选用了100水平6因素的均匀设计表,均匀设计表通过Matlab自动生成[13]。目标函数随着迭代过程而变化的情况见图2(a),可见很快接近收敛值。由序贯均匀设计得到的参数估计为
p1=0.3081,p2=2.6985,p3=0.4099,p4=0.1114,y1(0)=21.9886,y2(0)=34.5574,
目标函数值4631,图2(b)给出了根据估计参数用ode45()计算出的y1(t)的拟合曲线和数据分析。该问题在文献[16]中获得的最好结果为
p1=0.3190,p2=2.7010,p3=0.4190,p4=0.1031,y1(0)=22,y2(0)=39,
对应的最小二乘残差平方和为5076.6,大于这里的4631。
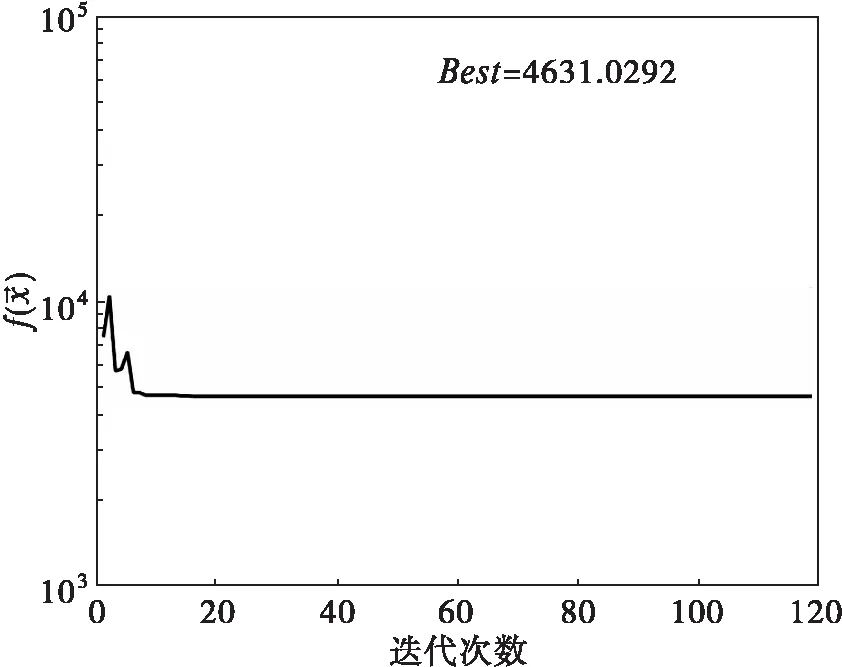
(a)目标函数值随迭代次数的变化
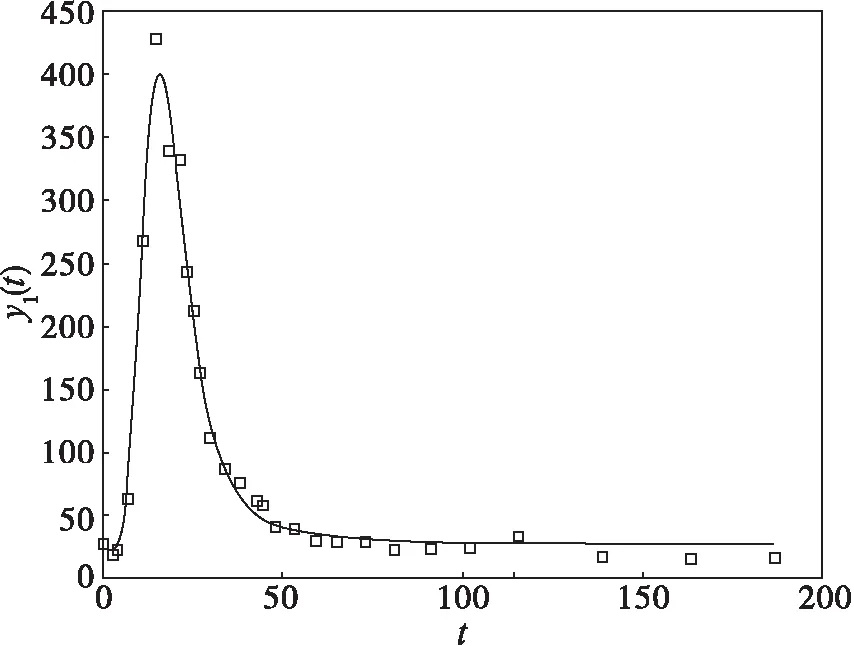
(b)由估计参数计算出的曲线和数据分布
例3一个7变量恒温连续搅拌槽反应器问题(continuously stirred tank reactor(CSTR) problem)的数学模型可描述为[17]
其中q=u4+u1+u2,u1,u2,u3,u4为方程参数。本例优化函数比较特殊,是求
的最大值,该问题实质上是一个最优控制问题[12]。这里目标函数PI需要求数值积分,可以用Simpson复化积分公式[15]。为便于和文献比较,初值取为
x0=[0.1883,0.2507,0.0467,0.0889,0.1804,0.1394,0.1046][17]。
参数范围取为
0≤u1≤20,0≤u2≤4,0≤u3≤6,0≤u4≤20。
这里选用100水平4因素的均匀设计表,均匀设计表通过Matlab自动生成[13]。编写程序运行后可得
u1=12.0485,u2=3.8651,u3=0.8317,u4=11.8667,
得到PI最大值19.8408。而在文献[16]中,
u1=11.4550,u2=4.5222,u3=0.6865,
设u4=6.0,对应PI最大值19.0437,本文计算结果有一定的改进。本题是求最大值,编程时把目标函数加负号,变为取为最小值。图3(a)显示的是最大值目标函数的相反数随着迭代次数增加而变化的情况,图3(b)显示了根据参数估计绘制的x1(t)~x7(t)数值解曲线。
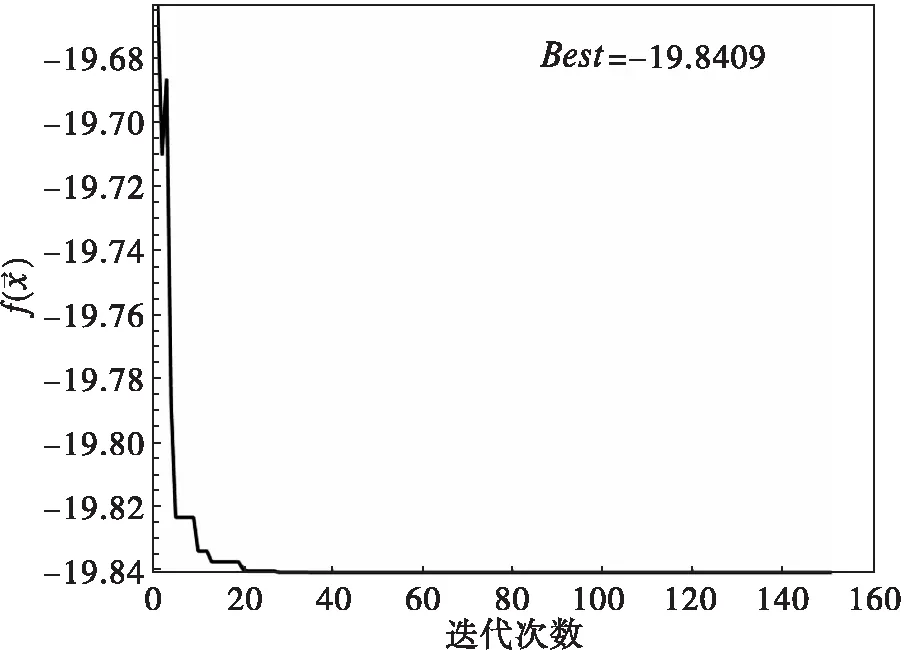
(a)目标函数随迭代次数变化
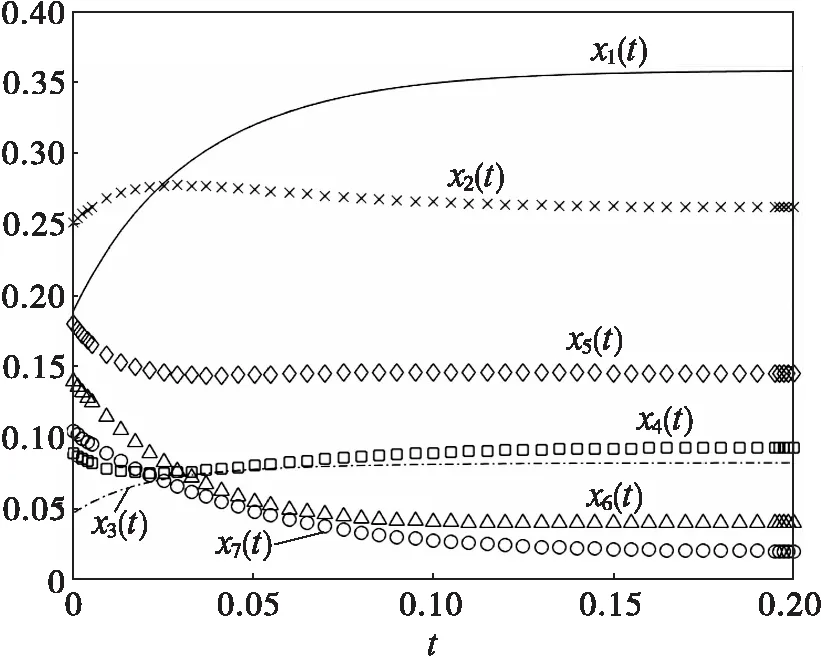
(b)根据估计参数绘制变量的曲线
与单点迭代和搜索算法相比,序贯均匀设计可以从多个均匀设计点同时开始迭代和搜索,具有本质上的并行性,因而效率会大大提高。
3 结论
针对含有非线性微分方程组初值问题的复杂参数估计问题,由于它们的目标函数的梯度很难计算,因而常使用无须梯度的直接搜索算法。本文使用搜索性能较好且计算机实现比较方便的序贯均匀设计方法对这一难题进行了探讨,通过三个典型应用,说明了方法的有效性。

