基于ONE-ESVM的入侵检测系统

胡希文，彭艳兵

（1.武汉邮电科学研究院，湖北武汉 430070；2.南京烽火天地通信科技有限公司，江苏南京 210019）

本世纪以来，随着网络技术的高速发展和网络规模的持续扩大，蠕虫和间谍软件等零日网络攻击变得越来越普遍与危险[1]。而现有的基于规则匹配的入侵检测机制常常由于其过于死板而不足以检测到这些攻击。因此，研究者们开发了基于异常检测的入侵检测方法来应对这类可以快速变异的攻击。

在各种入侵检测方法中，文献[2]研究了基于统计学方法的入侵检测，文献[3]的研究侧重于异常检测的理论措施，它主要研究了异常检测中的信息理论，如熵、条件熵、相对条件熵、信息增益等。文献[4]主要研究了基于基础机器学习算法如K-means 与KNN的入侵检测。

文中研究的主要是基于SVM的入侵检测方法。软间隔支持向量机由Cortes 提出，所以经常被称为C-SVM，它在分类问题中通常有很好的性能[5]。然而，软间隔支持向量机并不太适合用于检测网络流量中的新攻击，因为在监督学习过程中需要预先获取新攻击的特征信息，需要人为将这些流量数据分为正常流量和攻击流量，并分别贴上标签，导致了系统额外的时间和成本开销。因此，在入侵检测系统中可以考虑使用无监督学习的方法来进行异常检测。在SVM 家族里，适合这一场景的是单类支持向量机(One-class SVM)，它属于无监督学习算法。然而，在实际使用过程中，单类支持向量机有着假阳性率高的问题[6]，用其进行分类过后的数据，往往还需要进行第二次过滤才能有较好的效果，这无疑增加了系统的操作难度与复杂性。

1 数据集预处理

1.1 数据集介绍

文中采用加拿大纽布伦斯威克大学(University of New Brunswick,UNB)最新的入侵检测数据集CSE-CIC-IDS2018 作为训练与测试数据集，该数据集是当前入侵检测领域最前沿的数据集，相比于已有近二十年历史的DARPA 数据集和KDD CUP 数据集，该数据集无疑更贴近现在的网络环境，更具有实用性。

在CSE-CIC-IDS 之前，入侵检测数据集几乎都是以DARPA 和KDD CUP 为主。随着网络用户行为的变化以及网络入侵的逐步演变，现在这些很老的数据集已不再适合现在瞬息万变的动态网络环境。针对这一点，UNB的网络安全研究员们开发出了一种网络流量生成器和分析器工具CICFlowMerter，该工具使用Java编写，免费开源，可以在Github上获得。

CSE-CIC-IDS2018 数据集包括7 种不同的攻击场景，分别是暴力攻击(Brute-force)、心脏滴血漏洞攻击(Heartbleed)、僵尸网络攻击(Botnet)、DoS、DDoS、web 应用攻击集合(Web attacks)以及渗透攻击(Infilteration)，它的每条数据包含80 个特征[7]。

1.2 数据集提取与预处理

原始数据去重合并后得到7 873 490 条数据。在进一步处理过程中发现该数据集里面某几列数据是完全重复的，对于一个特征来说，如果所有样本中该特征的值都一样，那么它将不会对该模型的训练有任何影响。此外，还发现有一些行数据包含NaN与Infinity 这种无法进行数值化的数据。对这些数据进行清洗过滤后得到剩余的3 890 993 条数据，每条数据有70 个特征。清洗后的数据根据标签分布如表1 所示。

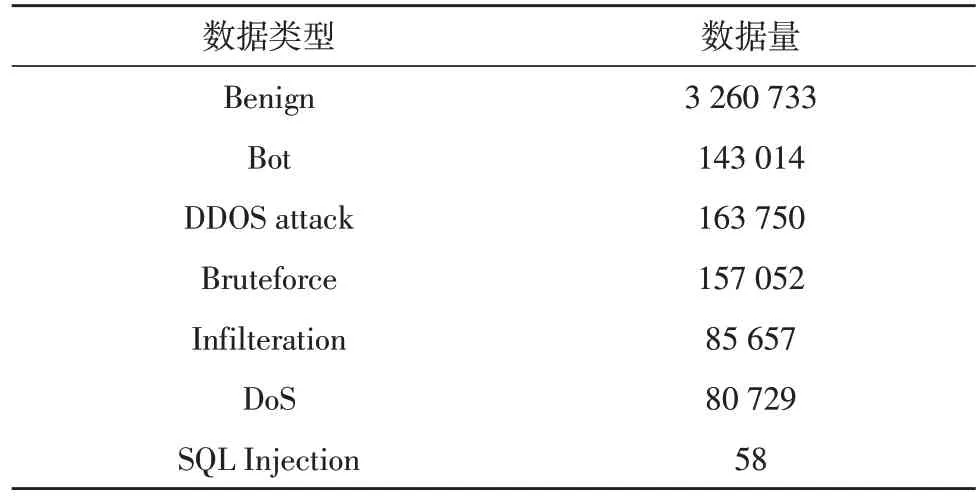
表1 数据集数据分布

由于SQL Injection 在原始数据中占比实在太低，若对其进行等比例取样，将得到个位数数量的样本，这样的数据量不适用于模型训练，故在抽取训练数据时，忽略掉SQL Injection 数据。

为了保证各类型数据占比与原数据一致，确保模型训练不会发生偏差，在训练模型和进行n-fold交叉验证时，在除去表1 中SQL Injection 数据之外的数据里，对每个类型的数据等比例随机抽取10%作为模型的输入数据集。

在机器学习模型中，有一些模型是对数值敏感的模型，数值的范围大小对它们的训练速度影响比较大，过大的数值范围可能会导致模型训练速度过慢。SVM 家族就是这类对数据范围敏感的模型，故需要对数据进行标准化处理[8]。文中采用Min-Max标准化，将数据映射到[0,1]的区间内：

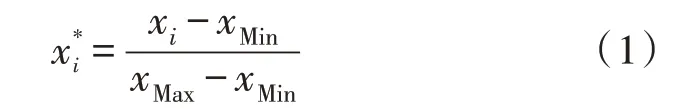
其中，xi为标准化之前的第i列特征数据，为标准化之后的第i列特征数据，xMin为第i列特征数据里面的最小值，xMax为第i列特征数据里面的最大值。

2 特征选择

2.1 遗传算法

为了加快训练速度以及得到更加准确的模型，文中在进行模型训练之前，使用遗传算法(Genetic Algorithm,GA)对输入数据的70 个特征进行特征选择。遗传算法的框架结构如图1 所示。

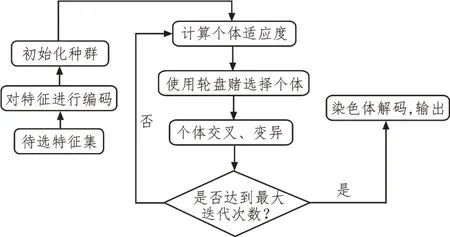
图1 遗传算法框架

由于文中使用遗传算法的场景是进行特征选择，即判断每个特征对于区分样本的贡献度[9]。对于一个特征来说，将不同类型的样本区分的越开越好，所以文中采用Fisher 线性判别法作为适应度函数。其核心思想是寻找一个最能反映类与类之间差异的投影方向，即要使得类间间距尽可能大，而类内间距尽可能小[10]，计算各类特征向量之间平均距离的公式为：

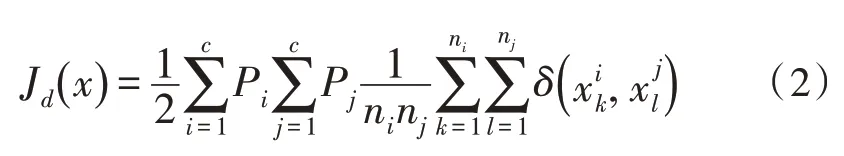
其中，c是类别的数量，Pi和Pj分别是类别i和类别j的先验概率，文中对于某类先验概率直接取其在原始数据中的占比；ni和nj是类别i和类别j的数量，在上一步对原数据进行抽样时就已确定；为向量空间中两个向量的距离度量，文中取欧氏距离作为度量，即：

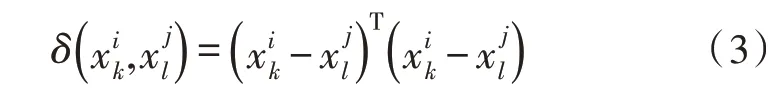
2.2 特征选择

输入的样本一共有70 个特征，设置初始种群大小为100，迭代次数为200，交叉率25%，变异率1%，然后观察特征选择结果，设特征选择数量为d，实验结果如图2 所示。

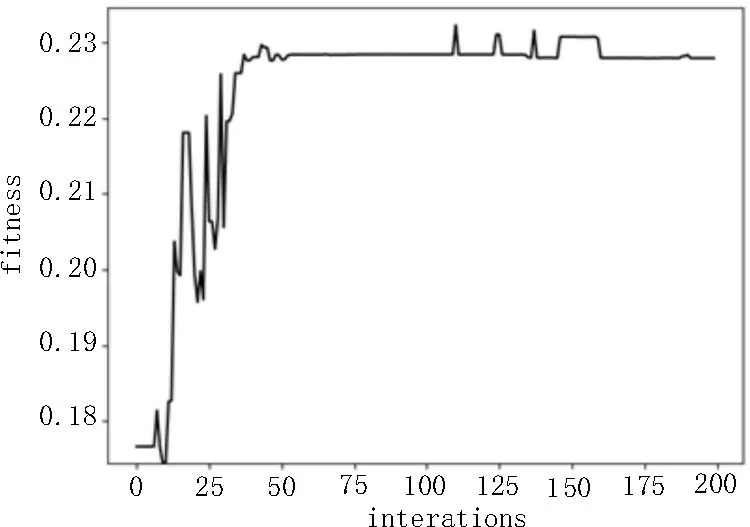
图2 选取特征数量为50个时的适应度

从图2 可以明显看出，随着遗传算法迭代次数增加，每一代种群的适应度在逐渐变大，当迭代次数到达一定次数时，算法会走向收敛。

然后扩展到选择所有个数特征的情况，将特征选择数量d从1 取到70，对每个d都进行10 次训练，一共训练700 次，每次训练的d都对应着一个最优适应度，将10 次训练的最优适应度取平均值，然后按照d从大到小排列，横向比较其最大平均适应度，结果如图3 所示。

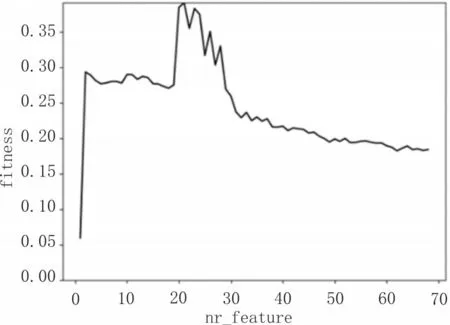
图3 选取特征数量与最高适应度的关系

从图3 可以看出，所选取的特征个数在35 个之前，最高适应度呈现出很大的波动，而在35 个之后，曲线相对平稳，最终适应度收敛在0.15～0.2 之间。

在上述获取最优适应度的过程中，对选出的最优特征进行计数统计，计算每个特征被选中的次数，结果如图4 所示。

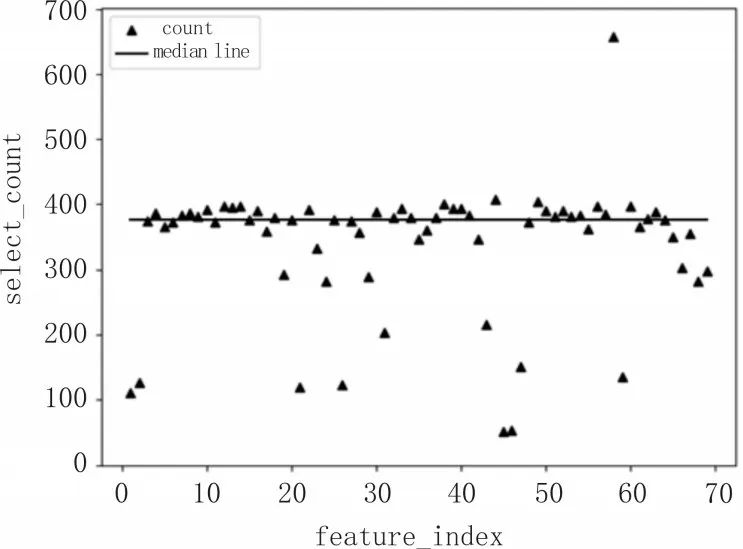
图4 每个特征被选中的次数

将700 次训练中每个特征被选中的次数作为每个特征的区分度，从图4 可以看出，大部分点都具有比较好的区分度，只有一些少数的点被选中的次数比较少。剔除掉低于中位线太多的点，可选出48个特征。

3 ONE-ESVM模型

3.1 Soft-Margin SVM

软间隔支持向量机，也叫C-SVM。它是在基础SVM 之上改进而成的。基础的SVM 也被称为硬间隔支持向量机，它主要有两个缺点，第一是不适用于线性不可分数据集，第二是对离群数据点敏感[11]。软间隔支持向量机引入一个松弛变量和一个惩罚参数C，它允许一些样本点跨越间隔边界甚至是跨出超平面，惩罚参数C的值限定了这个可以跨出的比例，它使得SVM 能够在线性不可分的数据集上进行扩展，于是SVM的优化问题变为：

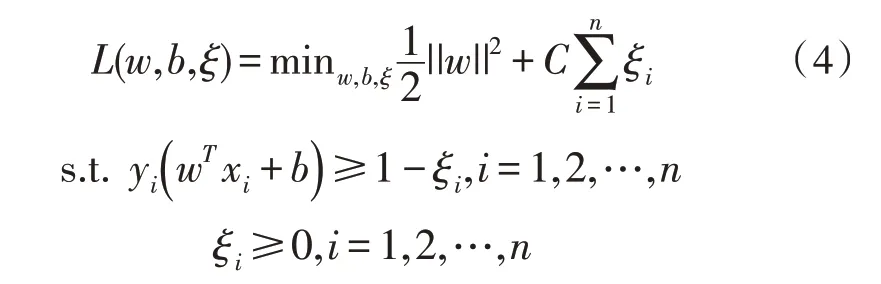
其中，ξi表示松弛变量，n表示样本总数，C为惩罚系数。由上述公式可知：

1）离群点i的松弛变量值ξi越大，该点离间隔边界就越远；

2）所有在分离超平面内的点的松弛变量ξi的值都等于0，即这些点都满足条件

3）惩罚参数C越大，意味着对离群点的惩罚就越大，也就是只允许更少的点跨过间隔边界，模型也会变得复杂，边界会收束的更紧；而C越小，则允许更多的点会跨过间隔边界，最终形成的模型边界也更平滑；

4）b的大小与分离超平面到原点的距离相关，b越大说明分离超平面离原点越远。

3.2 One-class SVM

One-class SVM 和一般的SVM 有所区别，它的核心思想是在样本空间中寻找一个分离超平面，将样本中的正例样本空间与其他样本空间分离开，预测时就用这个分离超平面作为决策标准，认为超平面内的样本是正例，超平面外的样本是反例[12]。它的优化函数为：

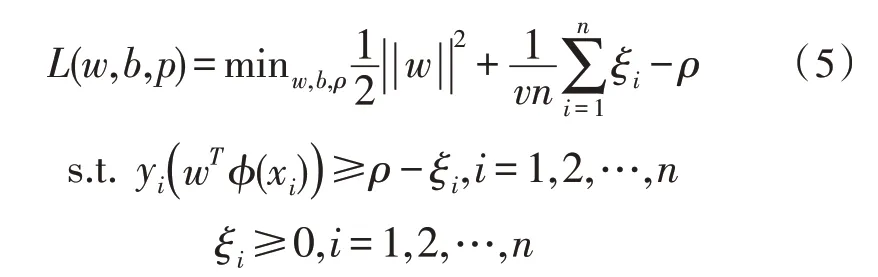
其中，ξi表示松弛变量，n表示样本总数，v类似于软间隔支持向量机中的C。由式（5）可知：

1）离群点i的松弛变量值ξi越大，该点离超平面边界就越远；

2）所有在超平面内的点的ξi值都为0，即这些点满足条件

3）v限定了异常点的比例上限，说明允许一定比例的点跨过超平面；

4）v限定了分离超平面的边界平滑度，更小的v值对应着收束更紧的边界；

5）ρ与分离超平面到原点的距离相关，ρ越大说明分离超平面离原点越远，它与软间隔支持向量机中的b功能一致。

3.3 ONE-ESVM

在日常实际网络使用中，绝大部分网络流量都是正常流量，异常流量的占比相对较小。那么，就实际检测而言，与正常流量相比，期望检测到的异流量的占比也就相对较小。所以从仅理论上来说，Oneclass SVM的思想似乎更适用于入侵检测。但是One-class SVM 在实际使用过程中并不是如此，它有一个很麻烦的缺点，那就是它不像软间隔支持向量机那么稳定，可能会出现很高的假阳性率，以至于将很多正常流量也识别成异常流量。针对这一点，文中将One-class SVM 进行改进，对其参数进行调整，使其分类超平面向分类性能更好地向软间隔支持向量机逼近。

由上述内容可知，在One-class SVM的优化函数中，与分离超平面位置相关的参数分别是||w||、ρ和由其优化函数可知，为了得到最优超平面，||w||需要尽可能小，ρ需要尽可能大与离群点相关，这与软间隔支持向量机是一致的。又由上文的对比发现参数v与参数C的功能基本一致，参数ρ与参数b功能基本一致，因此，可以使用参数C代替参数v，使用参数ρ代替参数b，于是得到如下优化模型：

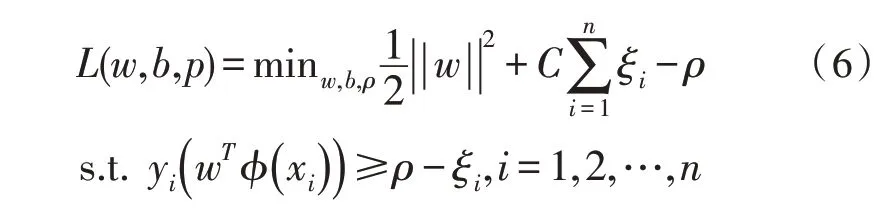
4 实验

4.1 数据集抽取

在文中实验里，数据集采用之前经过清洗过滤后的CSE-CIC-IDS2018 数据集，在特征选择之后，随机抽取其中的10%，提取的数据量对应类型分布如表2 所示。

表2 用来训练和测试的数据量

4.2 评价指标

在入侵检测中，比较重要的评价指标[13]有检测率(detection rate)、漏报率(missing report rate)和误报率(false alarm rate)。文中将检测率定义为检测出来的攻击数/总攻击数，漏报率为未检测出来的攻击数/总攻击数，误报率为正常流量被误认为是攻击流量/总正常流量，公式如下：

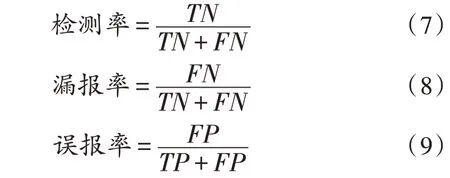
在实际使用中，系统将正常流量判定为攻击流量的情况是对用户影响最大的，故在保证高准确度的情况下，要严格控制误报率这一指标。

4.3 实验结果及分析

文中实验模型首先采用网格搜索法来寻找模型最佳参数，在寻找到最佳模型参数之后采用交叉验证的方式对模型进行验证。由于文中数据集选取的较大，故在进行交叉验证时，取n值为5，然后得到五轮不同的数据再取平均结果，实验结果如图5～7 所示，分别展示出了3 种不同的模型对于测试数据集中每种攻击的检测率、漏报率和误报率[14-20]。

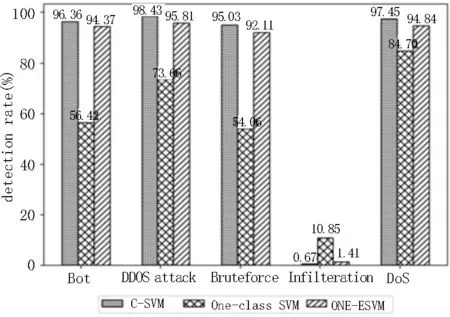
图5 检测率

从实验结果可以看到，3 种SVM 模型对于Infilteration 攻击的检测基本没用。经过调研发现，Infilteration 攻击的流量特征与正常流量特征非常相似，仅靠SVM 确实无法将其识别出来。

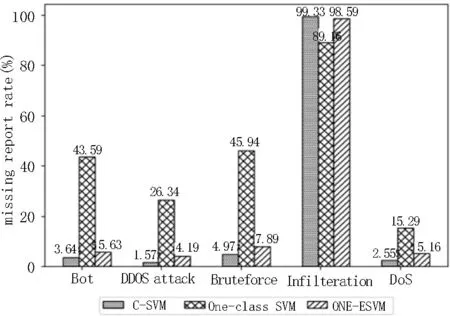
图6 漏报率

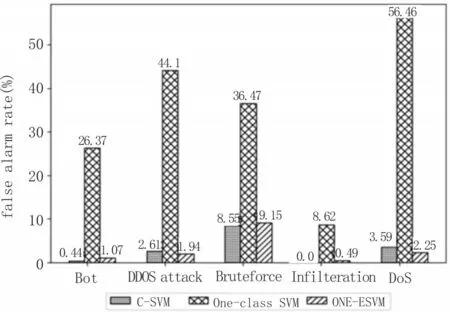
图7 误报率

在检测率与漏报率方面，软间隔支持向量机如逾期一样，拥有非常好的检测性能，它可以检测出绝大部分的攻击流量，只有很少的攻击流量没有被检测到；而对于One-class SVM 而言，其虽然具备无监督学习的特性，不需要对数据集做分类处理，但是由结果可知，其对于大部分攻击不具有很好的分类性能；对于文中提出的ONE-ESVM 模型，它的检测率与误报率非常靠近原生的软间隔支持向量机，从侧面证明了，它的分类超平面的确逼近了软间隔支持向量机。

在误报率方面，软间隔支持向量机对于大部分攻击来说，有着很低的误报率，完全可以满足现实使用需求；One-class SVM 如预期一般，有着非常高的假阳性率，它将大量的正常流量识别为攻击流量，这种超高的误报率在实际使用中是完全无法接受的；而文中的ONE-ESVM 模型有着与软间隔支持向量机相似的误报率，这在实际使用过程中完全可以被接受。

该实验结果说明了，在取得最佳参数的情况下，文中提出的ONE-ESVM 模型确实可以按照预期逼近分类性能很好的软间隔支持向量机，同时它也拥有了与One-class SVM 一样的无监督特征，使得获取数据集时更加灵活，而不用花费大量的精力去对数据集进行标记。

5 结束语

文中详细阐述了将改进的One-class SVM 应用到网络入侵检测系统中的情况，并详细介绍了传统的软间隔支持向量机模型和One-class SVM 模型，在此过程中使用遗传算法作为特征选择工具。

实验证明，改进后的One-class SVM 模型在不丢失其无监督学习特性的基础上确实能够对软间隔支持向量机进行逼近，使其分类性能和软间隔支持向量机一样好。