基于S 型加减速的六关节机器人速度平滑控制算法

韩媞

（大连东软信息学院智能与电子工程学院，辽宁大连 116023）

工业机器人在运动过程中需要联合控制多个轴的运动，并且会根据实时数据进行动态调整。为了获得良好的运动性能和精度，需要机器人运动轨迹具备高度平滑性、系统加减速具有高度柔性[1-3]。

六关节机器人在工业中应用广泛，经常用于拾取、搬运、焊接等场合。机器人有示教或离线编程两种工作方式。一般情况下，路径是通过给定若干个位置点来确定的[4-7]。那么，机器人在相邻两个轨迹的拐点处的速度处理就决定了机器人的运行速度和运行平稳性[8-11]，是影响机器人性能的重要因素。

目前，机器人运动系统中常用的加减速控制算法有指数、梯形、S 型曲线和三角函数等[12-14]。目前的设备中，在一些要求不高的场合，一般使用梯形加减速或指数型加减速控制，算法原理简单，但是在设备的启停阶段，其加速度不为零，所以会出现速度和加速度突变的情况，对大型设备冲击较明显，尤其不适用于工业机器人等高速运动系统的过程控制。由于S 型曲线加减速方法的速度和加速度变化连续，原理简单，易于实现，并且能够得出平滑的速度和加速度曲线，所以应用较广泛。文中通过使用S 型加减速原理来处理机器人在PTP（Point to Point）工作模式下拐点处的速度平滑过渡，实现了机器人快速、平稳、高精度的运动控制。

1 数学原理

1.1 S型加减速

S 型加减速是加减速控制中一个比较常用的方法[15-16]，该方法通过控制加加速度得到加速度曲线为梯形或者三角形，速度曲线为“S”型，从而使速度曲线变化柔和，控制加加速度值减小冲击，其加速度曲线如图1 所示，分为3 个阶段，加加速度阶段、匀加速阶段、减加速阶段，对应的速度曲线如图2所示。

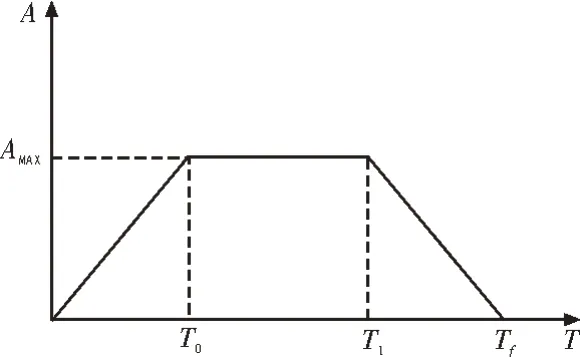
图1 加速度曲线图

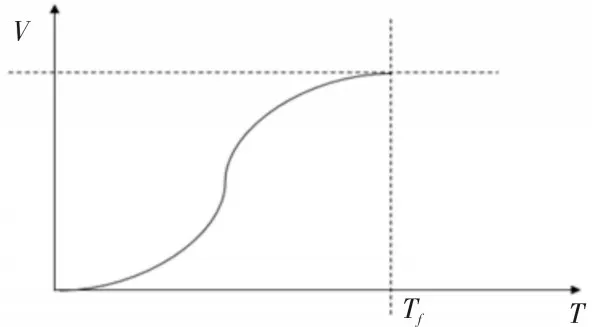
图2 S型速度曲线图

通过约束最大加加速度JMAX值，来控制加减速过程中产生的冲击，从而得到S 型速度曲线，加速度公式如下所示：

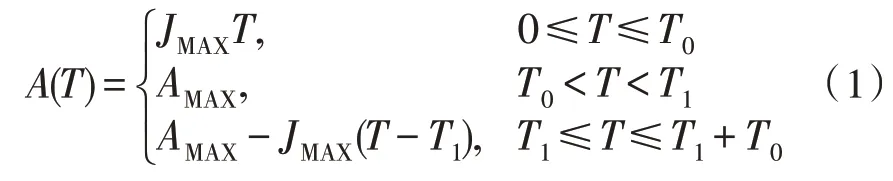
由微积分原理可以得到速度公式如式（2）所示，其中，V0为初始速度。

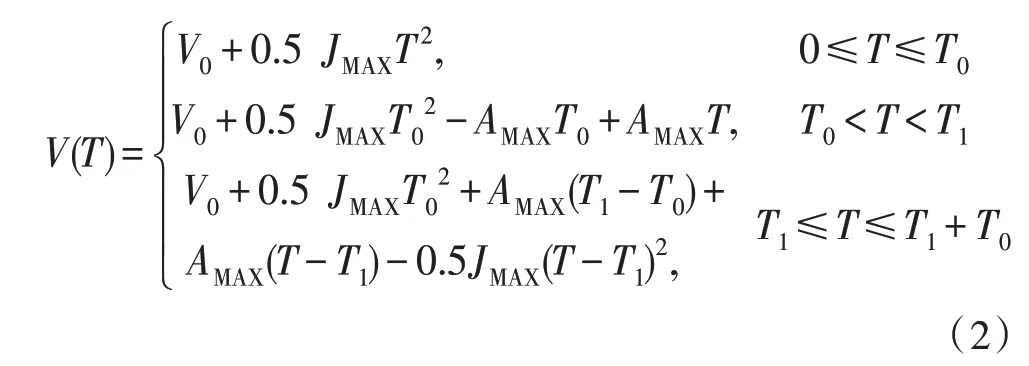
由积分原理可得距离公式如式（3）所示，其中，V0为初始速度。

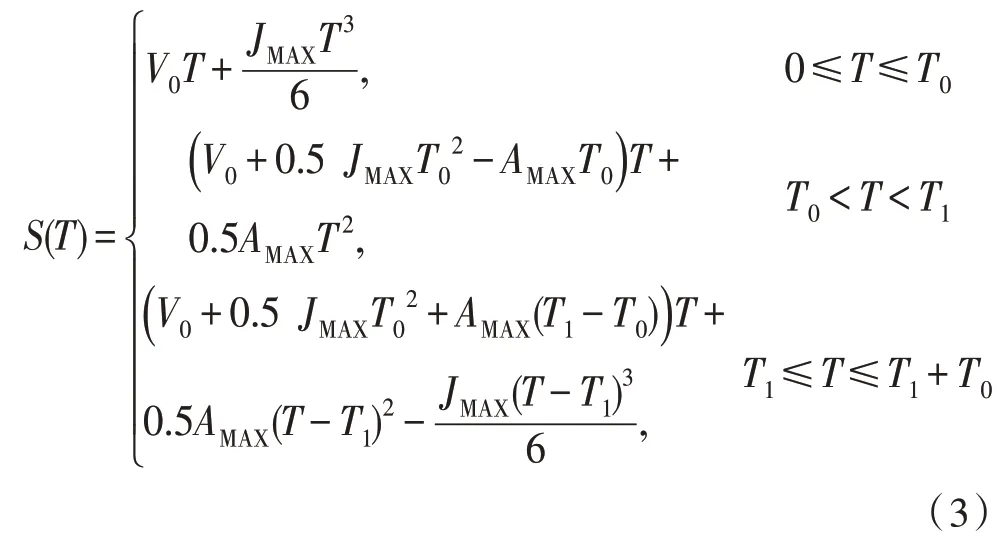
1.2 过渡算法

在拐角前后的路径中，六关节机器人各个物理轴的速度可以分别设定为，其中上标表示第几个轴，下标表示第几段轨迹的速度。各个轴的速度如图3 所示。

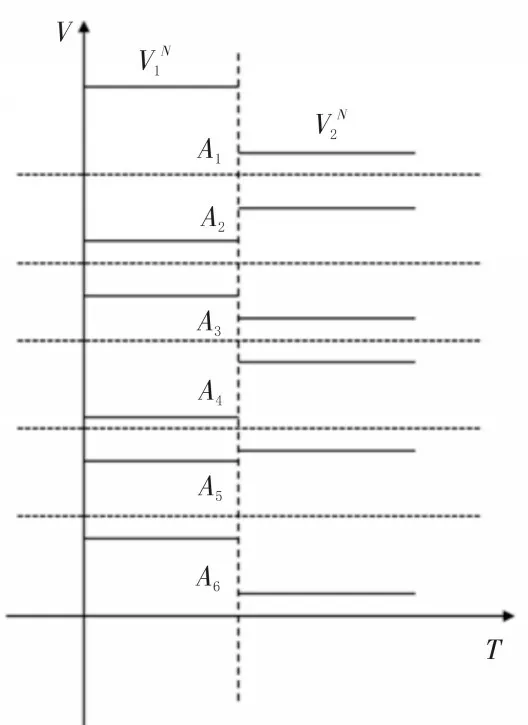
图3 物理轴速度曲线

从图3 中可以看到，不同轨迹段中各个物理轴的目标速度是不同的。拐角速度平滑处理的主要思路就是在保证误差的基础上，每个物理轴各自计算在拐角处从前一段的V1N到下一段的V2N的平滑过渡过程。

速度控制的要求是每个物理轴的速度变化要平顺，不能超过各自给定的最大加速度和加加速度的约束。在拐角处对各物理轴分别进行S 型加减速就可以达到目的，如图4 所示。

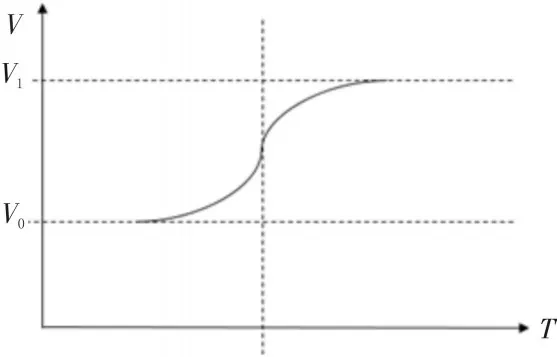
图4 单个物理轴的速度过渡示意图

过渡算法不仅要保证加速度和加加速度不超过给定约束，还需要保证机器人各物理轴在运动过程中的误差在给定的约束范围内，从而确保机器人端部位置在误差约束范围内[8]。

通过给定各个轴的最大误差约束和最大加速度以及加加速度约束，保证所有物理轴的过渡时间保持一致。通过计算各个物理轴的速度差和约束条件，计算出每个物理轴需要的过渡时间，取最大的过渡时间作为统一过渡时间，再根据该时间修正每个物理轴在过渡过程中所需要的临时最大加速度和加加速度，作为当前过渡计算的条件值，最终完成过渡过程的计算。

1.3 具体计算

假设各轴的最大误差为δ，一般情况下各个轴可以设置成一样的误差值，设成不同的误差值也可以，不影响后续的计算。为简单起见，这里设置成相同的误差值。

假设各个物理轴的加速度约束为an，其中n表示第n个轴，Jn为各个轴的加加速度约束。

根据各个物理轴两段轨迹的速度差值、最大加速度值和加加速度约束值可以得到一个过渡时间Tn。

为了保证轨迹的正确性，各个物理轴需要保证时序上的统一，因此需要确定最终统一的过渡时间TF=MAX(T1,T2,T3,T4,T5,T6)。完成统一过渡时间的计算后，各个物理轴再根据时间计算当前过渡段所需要的加加速度值和最大加速度值。

单个物理轴的误差值Sδ的计算公式如式（4）所示：

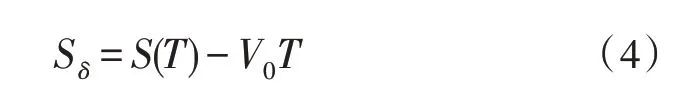
过渡部分最大误差示意图如图5 所示。

图5 过渡部分最大误差示意图

可见Sδ为偏离原轨迹的距离，原轨迹为单个物理轴通过程序指定的轨迹，其速度曲线是确定的，当速度偏离原速度曲线后，产生的偏离距离即为误差。

由于在过渡过程中S 型加减速在拐点两侧的速度与原始速度曲线在时间上是对称的，因此最终过渡后单个物理轴的误差会消除掉，机器人最终回到了原始轨迹上。

T0到T1之间是过渡时间，在这段时间内非S 型过渡的距离是S1，使用S 型过渡的距离是S2，如图6 所示，这两段距离是相等的，单个物理轴的误差值是可以忽略的。

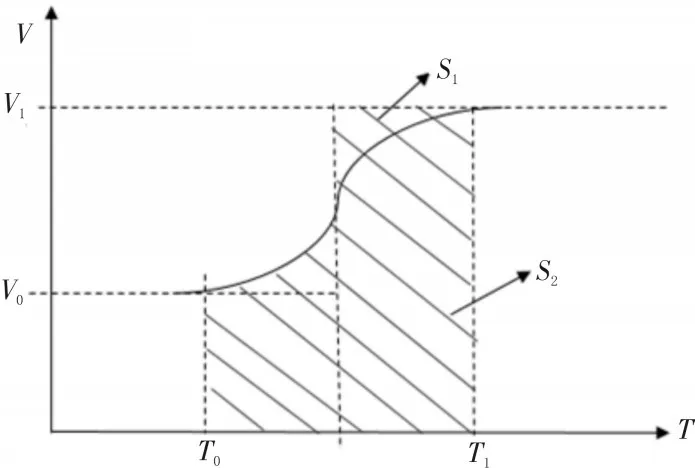
图6 过渡部分整体误差示意图

2 实验验证

实验条件：有两段机器人运动的轨迹以及进给速度，使用C++开发环境VS2013 进行编程，根据各个物理轴第一段和第二段的速度，按照插补周期为2 ms 计算出过渡过程中的插补数据。

根据插补数据画出各个物理轴的速度曲线，来证明在过渡过程中各个物理轴的速度、加速度以及误差值都不超过限定值，从而证明该算法的正确性。

在机器人随机运动过程中，随机选取拐点的3 个轨迹点的六轴空间内的坐标如下所示：

其中，Ai代表机器人的第i个轴坐标。

进给速度F=10 000 mm/min，按照PTP 模式第一点到第二点的轨迹段中，各个物理轴的速度由公式计算得到：

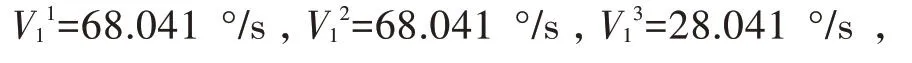
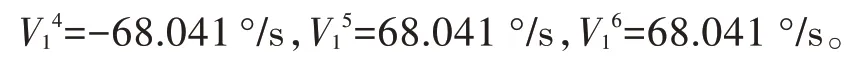
设6 个物理轴的最大加速度约束值为100 °/s2，最大加加速度约束值为1 000 °/s3。计算可得过渡时间为0.2 s。

6 个物理轴在两段之间速度变化最大值为136.082 °/s，根据加加速度约束值，可以得到一个加速度三角形，如图7 所示。

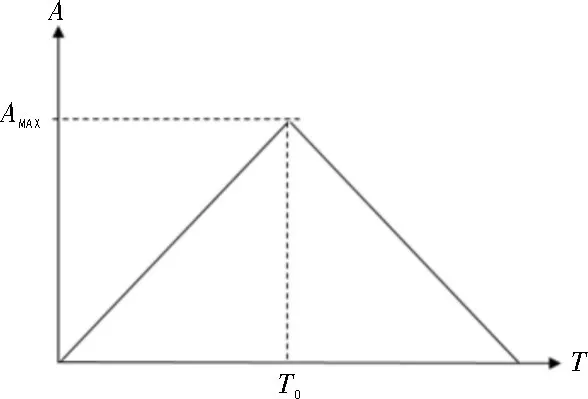
图7 实际过程的加速度示意图

加速度三角形斜率为加加速度限制值，三角形面积为速度差值，由此可以计算得到AMAX=3.687 8 °/s2，T0=0.036 878 s。

A1～A6的过渡速度曲线如图4 所示。由此进行速度插补，得到各个物理轴的实际插补速度如图8 所示，实际插补加速度如图9 所示，图中由上至下分别为A1～A6轴的速度和加速度。

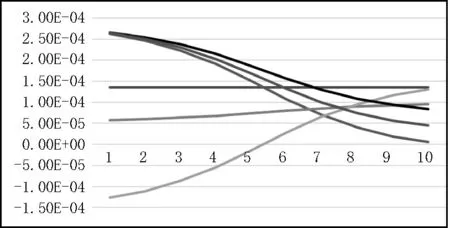
图8 实际插补数据速度示意图

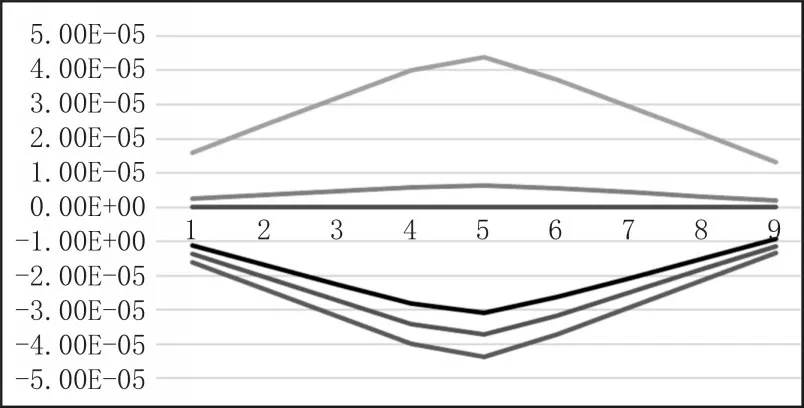
图9 实际插补数据加速度示意图

过渡过程中各个物理轴的最终误差均为0，最大误差如下所示：

ERROR1=0.000 000 00，ERROR2=0.000 264 336，ERROR3=3.887 3×10-5，ERROR4=0.000 264 336，ERR OR5=0.000 186 59，ERROR6=0.000 225 463。

实际验证的最终误差符合理论分析结果，最大误差控制在10-4范围内，满足了机器人实际运行的精度误差约束要求。

3 结论

在工业机器人运动控制系统中，需要6 个轴的位置在拐点处的速度控制稳定，系统加速度变化较小。直线型、梯形或指数型加减速等算法在运动过程中会出现速度和加速度的突变，不适于大型设备如工业机器人等系统。为了改善六关节机器人的动力学性能，文中提出了S 型加减速的控制算法并使用实际的机器人运动数据进行了C 程序的验证。最终根据实际插补点的数据计算各个物理轴的速度、加速度、加加速度和最大误差，证明了使用S 型速度变化曲线作为控制机器人各个物理轴的速度变化规律，既可以满足各物理轴的加速度和加加速度的极限值约束，也可以满足机器人轨迹的误差约束，实现了对机器人良好、平滑的速度控制。