ARIMA模型在预测前列腺穿刺人数以及穿刺阳性率中的应用
邱瑞莹,杨 芬,摆俊博,王路路,陶 宁,3
(新疆医科大学1公共卫生学院;2第一附属医院泌尿外科;3临床博士后流动站,乌鲁木齐 830011)
前列腺癌是一种在世界范围内流行的,中老年男性易患的恶性肿瘤,近年来我国前列腺癌的发病率与死亡率均呈现快速上升的趋势[1],早期诊断对提高前列腺癌生存率、改善预后具有重要意义,前列腺穿刺是前列腺癌诊断的金标准[2],2009-2017 年新疆新诊断前列腺癌患者不断增多[3],若能预测前列腺穿刺人数以及穿刺阳性率,则能够根据预测结果提前部署安排相关医疗资源。自回归积分滑动平均模型(autoregressive integrated moving average,ARIMA)是时间序列分析的基本模型之一,对短期预测有较好的效果[4]。目前ARIMA 模型常用于预测疾病发病率与流行趋势、就诊人数及医疗资源消耗量等等[5-7],曾被证实可较好地预测恶性肿瘤的发病率以及住院率[8-9],但目前较少研究将ARIMA 模型应用于前列腺穿刺情况的预测。本研究依据2007-2017 年新疆医科大学某附属医院前列腺穿刺人数以及穿刺阳性率,建立ARIMA 预测模型,并通过对2018 年穿刺人数以及阳性率进行预测,将模型预测值与真实值进行比较,评估模型的预测效果。
1 资料与方法
1.1 资料来源收集新疆医科大学某附属医院泌尿外科2007-2018年所有行前列腺穿刺术患者的信息,按季度对数据进行分析。1-3 月:第一季度Q1;4-6月:第二季度Q2;7-9月:第三季度Q3;10-12月:第四季度Q4。
1.2 ARIMA 模型的建立[10-11](1)分析时间序列情况,并进行平稳化处理:根据原始序列图判断序列是否平稳,不平稳,则对序列的趋势或季节性趋势进行差分或季节差分处理使其平稳。(2)模型识别:绘制经平稳化处理后序列的ACF 和PACF 图,根据拖尾或截尾情况为目标模型进行定阶。(3)模型参数估计与检验:对可能的模型进行纯随机性测试,若测试结果P<0.05,则此模型信息提取不完整,排除该模型,对P<0.05 的模型继续做参数显著性检验,保证各参数均显著非零。对备选模型进行参数估计与假设检验,并采用标准化的贝叶斯信息准则(Bayesian Informa‑tion Criterion, BIC)以及R2确定最佳模型,BIC越小,R2越大时模型拟合度越好。然后,根据Ljung-Box 统计量有无统计学意义对模型的残差序列进行白噪声诊断判定。(4)模型预测:运用选定模型进行预测,并计算95%CI以及相对误差。
1.3 统计学处理应用Epidata 3.1建立数据库,用百分率表示穿刺阳性率,利用SPSS25.0 建立穿刺人数以及穿刺阳性率的ARIMA 模型,采用标准化BIC 以及R2确定最佳模型,使用筛选出的最优模型对穿刺人数及阳性率进行预测,根据实际值是否落在预测值的95%CI内和平均相对误差对模型的拟合能力进行评价。
2 结果
2.1 前列腺穿刺人数ARIMA模型预测
2.1.1 ARIMA 模型的选择 本次研究收集2007-2017 年行前列腺穿刺术患者的信息,按季度进行分析,原始序列图显示该序列具有明显的趋势性和季节性(图1 左),故选用ARIMA 乘积季节模型,即ARI‑MA(p,d,q)(P,D,Q)S。序列季节周期为4 个季度,即S=4,因进行了1阶差分和1阶季节差分,得出d=1,D=1,再绘制2007-2017年差分处理后的序列图,可见经差分处理后为平稳序列(图1 右)。根据ACF、PACF 图(图2),可分析出p 可能取0、1 或2,q 可能为1 或0,P和Q 可能为0 或1,共有24 种可能的模型,对其进行纯随机性测试,排除测试结果P<0.05 的模型,对剩余的可能模型做参数显著性检验,剔除所有参数可能同时为0 的模型,最后余11 种备选模型,根据BIC 准则,以及R2值选取最适合的模型(表1)。本研究中筛选出的最优模型为ARIMA(0,1,1)(1,1,0)4,BIC=5.961,R2=0.604,该模型Ljung-Box 的Q统计量为14.568,无统计学意义(P=0.556>0.05) ,说明残差是随机分布的,模型充分提取了原序列中的数据信息,适用于前列腺穿刺人数的预测。

表1 穿刺人数ARIMA模型定阶

图1 穿刺人数的原始序列图(左),差分处理后序列图(右)

图2 一阶差分和一阶季节差分后的ACF(左)和PACF(右)图
2.1.2 模型拟合及预测 应用ARIMA(0,1,1)(1,1,0)4模型对2018 年前列腺穿刺人数进行预测,结果见表2、图3,所有实际值均落在预测值的95%CI内,平均相对误差为14.46%,预测模型拟合效果较好。

图3 前列腺穿刺人数ARIMA(0,1,1) (1,1,0)4模型拟合效果图

表2 2018年各季度穿刺人数预测/例
2.2 前列腺穿刺阳性率ARIMA模型预测
2.2.1 ARIMA 模型的选择 原始序列图显示该序列具有明显的趋势性,但是并不具有季节性(图4 左),故选用ARIMA 非季节性乘积模型,即ARIMA(p,1,q)。根据2007-2017年差分处理后的序列图,可见在进行了差分处理后,为平稳序列(图4 右)。根据绘制的ACF、PACF 图(图5),分析p 值可能为1 或0,q 值可能为1或0,共有4种可能的模型组合,排除测试结果P<0.05 的模型,对剩余的3 种模型做参数显著性检验,剔除所有参数可能同时为0 的模型后剩余3 个备选模型,再根据BIC 准则以及R2选取最适合的模型,本研究中筛选出的最优模型为ARIMA(1,1,1),BIC=4.988(表3),R2=0.558,该模型Ljung-Box 的Q统计量为6.891,无统计学意义(P=0.975>0.05) ,说明残差是随机分布的,模型充分提取了原序列中的数据信息,适用于前列腺穿刺阳性率的预测。

表3 穿刺阳性率ARIMA模型定阶
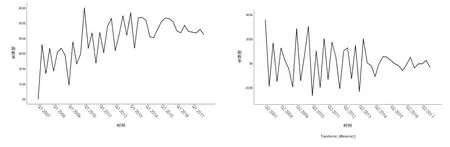
图4 穿刺阳性率原始序列图(左),差分处理后序列图(右)

图5 一阶差分和一阶季节差分后的ACF(左)和PACF(右)图
2.2.2 模型拟合及预测 应用ARIMA(1,1,1)模型对2018 年前列腺穿刺阳性率进行预测,结果见表4、图6,所有实际值均落在预测值的95%CI内,其平均相对误差为31%,根据图6 可看出预测值和真实值的动态趋势基本一致,说明预测模型拟合程度较好。

表4 2018年各季度穿刺阳性率预测/%

图6 前列腺穿刺阳性率ARIMA(1,1,1)模型拟合效果图
3 讨论
时间序列分析是探索在某一时间序列中包含的所有信息,寻找其在长期变动过程中所存在的统计规律,并通过建立统计模型实现预测并调控将来事件的目的[12],ARIMA 是由美国学者Box和英国统计学者Jenkin提出的重要时间序列分析预测模型,称为自回归滑动平均混合模型,它主要对两个问题进行解答:(1)分析时间序列的随机性、平稳性和季节性;(2)在时间序列分析的基础上,选择适当的模型进行预测。但是ARIMA 模型是通过基于历史数据上的数学模型来进行预测,无法考虑其他外部因素的影响,比如国家政策的改变与调整、突发事件等[13]。前列腺癌是中老年男性高发的恶性肿瘤,在恶性肿瘤中具有很高的死亡率,流行病学数据显示前列腺癌的发病率将会持续呈现上升的趋势[14]。
本研究中观察到2007-2017 年前列腺穿刺人数与阳性率均呈现上升趋势,与其他地区观察到的数据一致[15],1、2 季度的穿刺人数要多于3、4 季度,而穿刺阳性率并不具有明显的季节性,在建立模型的过程中我们筛选出ARIMA(0,1,1)(1,1,0)4与ARIMA(1,1,1)模型分别为前列腺穿刺人数与穿刺阳性率的最佳拟合模型,在对2018年穿刺人数与阳性率进行预测时,真实值均落在预测值的95%CI内,且预测值和真实值的动态趋势基本一致,说明预测效果较好,ARIMA模型可以用于对前列腺穿刺人数以及阳性率的预测。前列腺穿刺术需专科医生进行,若穿刺结果为阳性,前列腺癌的后续治疗需要手术操作或针对性的药物治疗,建立前列腺穿刺人数及穿刺阳性率的预测模型不仅有助于医院合理的安排手术室、操作人员以及医疗资源,同时近年来由于前列腺癌患者的增加以及死亡率的上升,很多专家提出针对前列腺癌应提倡“三早”预防[16],预测模型可帮助相关部门从宏观角度观察对前列腺癌防治措施的效果,而本研究认为随着未来前列腺癌患者可预测的增多,还需采取措施提高前列腺穿刺人数,尽可能做到疾病的早诊断,早治疗。
综上所述,ARIMA 模型可以用于对前列腺穿刺人数以及穿刺阳性率的预测,目前国内针对前列腺癌数据的ARIMA 模型较少建立,本研究数据来源可靠,数据的稳定性、连续性较好,符合建立ARIMA 模型的条件,但受ARIMA 模型本身特点与资料可获得性的限制,本研究存在一定的局限性,该模型易受外部突发因素影响,造成预测结果出现误差,因此在实际应用中应尽可能收集更长期的数据,需考虑的更加全面,不断修正和拟合更接近实际的模型,以得到满意的预测结果。

