基于GRNN算法的船舶轨迹分析方法
蒲 实,程广福,余桐奎
(大连测控技术研究所,辽宁 大连 116000)
0 引 言
无论船舶是靠泊还是在航状态,由船载设备以及岸基基站共同构成的船舶自动识别系统都会每隔2~360 s(报告频率随不同的船舶行为状态而定)更新播报一次。船舶自动识别系统由VHF通信机、船载显示器、GPS定位仪以及传感器等相连接的通信控制器组成[1],结构如图1所示。由AIS系统的结构图可知,该系统能自动交换包括船位、航速、航向、船名、呼号等重要信息,在发送这些信息的同时,接收VHF通信机覆盖范围内的其他船舶发送的信息,实现了自动应答。作为一种开放式数据传输系统,还可与雷达、电子海图与信息显示系统(ECDIS)等终端设备进行连接,实现信息交互,有效减少了船-船、船-岸的碰撞事故,在很大程度上避免了因海上碰撞事故造成的人员伤亡、财产损失以及海洋环境的污染[2]。
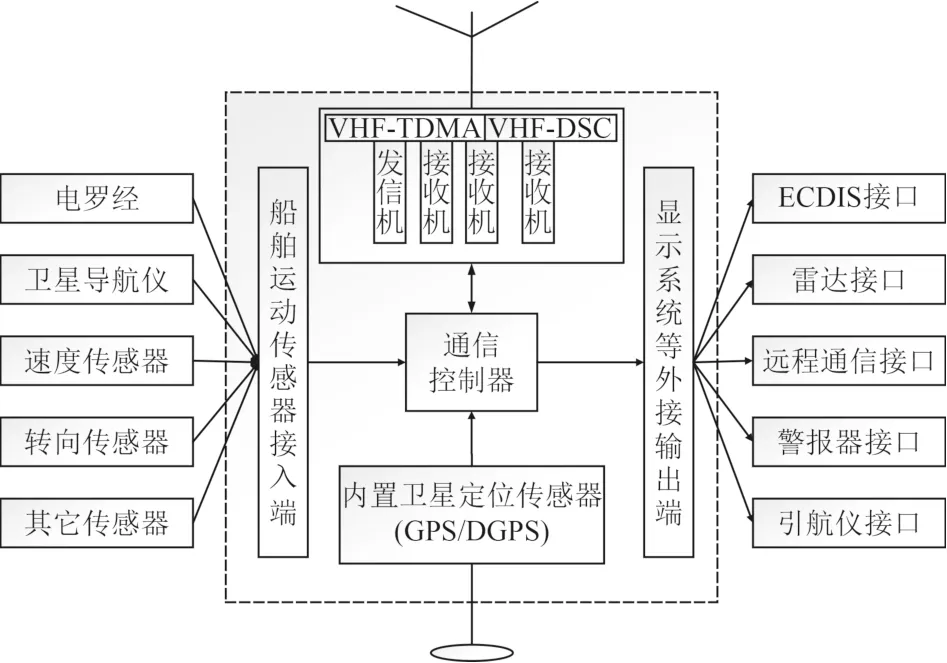
图1 船舶自动识别系统的组成结构图Fig. 1 Composition and structure of ship automatic identification system
1 轨迹分析原理
AIS信息依靠无线电波进行数据传输且具备时空特性,传输过程中易受系统数据丢包、船员操作不当、异常数据传输等因素影响,从而造成岸基基站接收到的数据在时间上不完整。因此,船舶的轨迹分析处理问题变成了AIS数据的恢复问题。现有的AIS数据分析处理方法大多基于AIS数据特性的插值分析法,例如结合AIS信息中的航速航向或时间的拉格朗日线性插值法、最邻近插值法、三次样条插值法等方法。具体步骤是将AIS报文按照AIS技术特性ITU-R M.1371标准进行解码,经过数据的预处理得到能够使用的点,这些点包含了船舶在各个时刻上的船位(经纬度)、航速、航向等信息。然后依据时间顺序整理,通过各类算法补全某些时刻丢失的点,最后绘出船舶的轨迹散点图。但是使用各类算法时会存在一定的不足:例如最为常用的一种方法线性插值(Linear)算法,其执行速度较快,有足够的精度但是不够高;三次样条插值(Spline)算法,其执行速度最慢,但是精度高,最为平滑;最邻近插值(Nearest)算法,其执行速度最快,但是数据平滑很差,插值所得的数据不是连续的[3]。
综合轨迹数据的处理分析过程,可进一步将该类问题抽象为近似二维平面的非线性函数曲线点拟合逼近问题,而广义回归神经网络(GRNN)算法在函数点拟合逼近问题上具备其他神经网络不具备的优点,如很强的非线性映射能力和学习速度,网络最后收敛于样本量集聚较多的优化回归,样本数据少时,预测效果很好,网络还可以处理不稳定数据,十分契合AIS的数据特点。本文在现有的插值方法线性插值的基础上引入GRNN算法形成一种新的L-GRNN算法。
2 L-GRNN算法模型
2.1 GRNN理论
假设x,y是2个随机变量,其联合概率密度为f(x,y) , 若 已 知x的 观 测 值 为x0,则y相 对 于x的 回 归,也即条件均值为[4]:

式中:n为样本容量,p为随机变量x的 维数。σ在这里称为光滑因子,是高斯函数的宽度系数。将式(2)与(3)代入式(1),并交换积分与求和的顺序,得
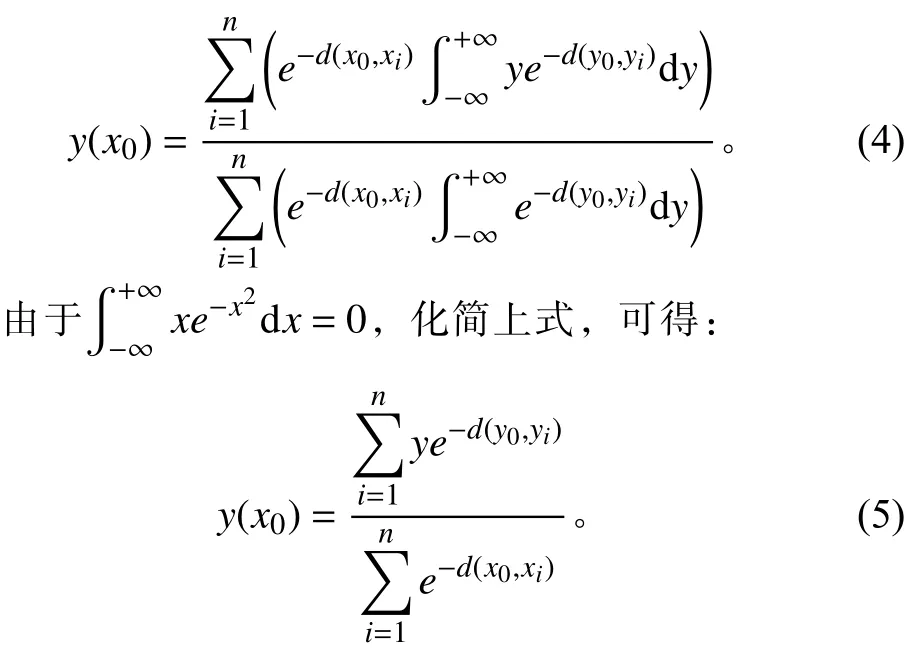
GRNN网络结构有4层,分别是输入层(imput layer)、模式层(pattern layer)、求和层(summation layer)和输出层(output layer),其结构如图2所示。对应网络输入为X=[x1,x2,···,xn]T, 其输出为Y=[y1,y2,···,yk]T。
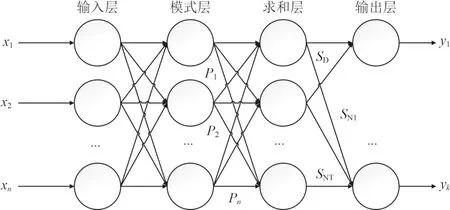
图2 GRNN网络结构图Fig. 2 GRNN network structure
2.2 L-GRNN算法模型
船舶的轨迹在二维平面内可认定由直线轨迹段与曲线轨迹段构成,具体的评判标准为插值点附近航向差值的绝对值是否在 5°以内,若在,判定该轨迹段为直线轨迹段,否则判定为曲线轨迹段[3]。基于该理论,L-GRNN的核心思想即在直线轨迹段考虑时间权重进行线性插值,在曲线轨迹段考虑使用GRNN算法进行插值。线性插值算法的基本原理如下[5]:
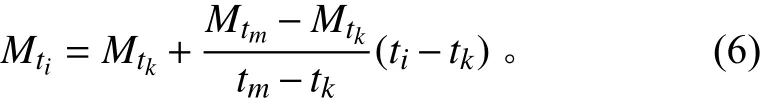
其中,缺失点数据为 (ti,Mti) ,ti代表缺失点数据的时刻,Mti代 表相应时刻对应的数据,ti前 一时刻tk的数据与后一时刻tm的数据已知,依照上式处理,即为线性插值算法。
L-GRNN算法实现步骤主要分为3步,技术流程如图3所示。
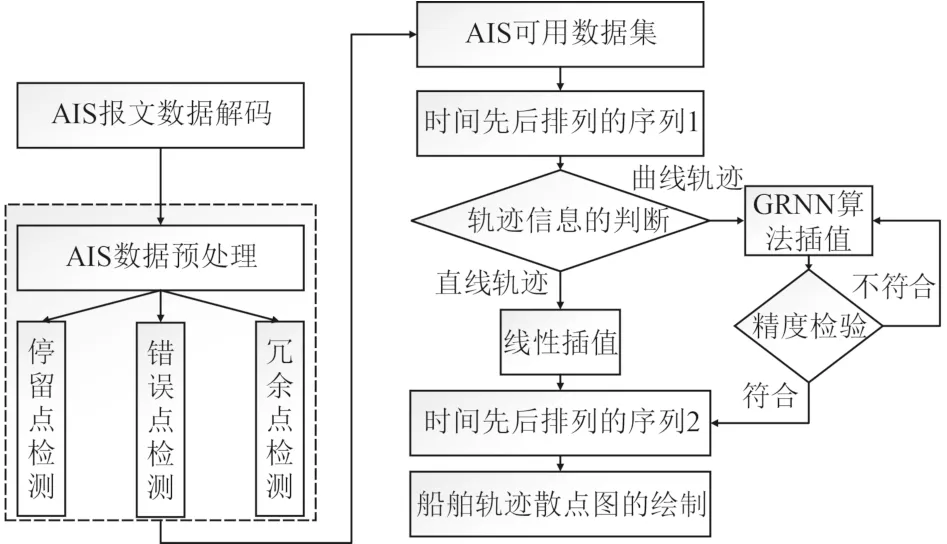
图3 算法技术流程图Fig. 3 flow chart of algorithm technology
1)AIS数据的预处理
该步骤是为了得到可以直接进行数据处理的AIS数据集。首先将原始的AIS报文信息依据AIS技术特性ITU-R M.1371报文要求进行解码;接着进行数据的预处理,对解码出来的数据进行包括停留点检测、错误点检测、冗余数据点检测,数据进行筛选时依照以下规则进行:
① 错误点的检测规则。MMSI码的位数小于9位的记录无效、纬度大于90°或者小于-90°的记录无效、经度大于180°或小于-180°的记录无效。
② 停留点的检测规则。船舶处于泊位、锚地等地时的AIS记录无效。
③ 冗余点的检测规则。保证数据量的情况下重复的AIS记录无效。
2)AIS数据的恢复
该步骤是为了恢复缺失的AIS数据。首先整理数据集,将数据依据时间先后顺序进行排列;然后找出需要进行数据恢复的点,依据船舶轨迹的判别方法,判别需要进行插值处理的段为直线段还是曲线段。若为直线段,采用线性插值进行数据恢复,反之采用GRNN算法进行数据恢复。最后依据插值点两端的端点航向可判别所得插值点是否在2个航向的交界以内区域即精度是否满足要求,若满足要求,进入下一步,否则调整网络参数,重复本步骤。
3)AIS数据点的可视化
该步骤是为了轨迹点的可视化。将所得的时间序列点在二维坐标平面进行标注,使用Matlab绘制各个数据点散点图,从而恢复船舶的轨迹散点图。
3 仿真分析与结论
GRNN神经网络算法在理论上可以逼近任意函数,理论研究表明GRNN网络作为RBF(径向基)网络的一种变化形式,在逼近能力以及学习速度上其效果比其他的神经网络算法好[6]。选取一系列的离散数据点类比离散的船舶轨迹点,应用GRNN算法进行离散点的逼近及拟合,仿真过程如下:
实验仿真考虑逼近拟合y函数的8个数据点,其坐标点分别为(2,0),(3,1),(4,2),(5,3),(6,2),(7,1),(8,2),(9,1)。首先作出其散点图如图4(a)所示;接着使用 Matlab的Neural Network工具箱搭建出y广义回归神经网络,使用略低于 1 的y的 SPREAD值(即输入值之间的距离,但该值可调),可得到与各数据点拟合程度很高的y函数如图4(b)所示。
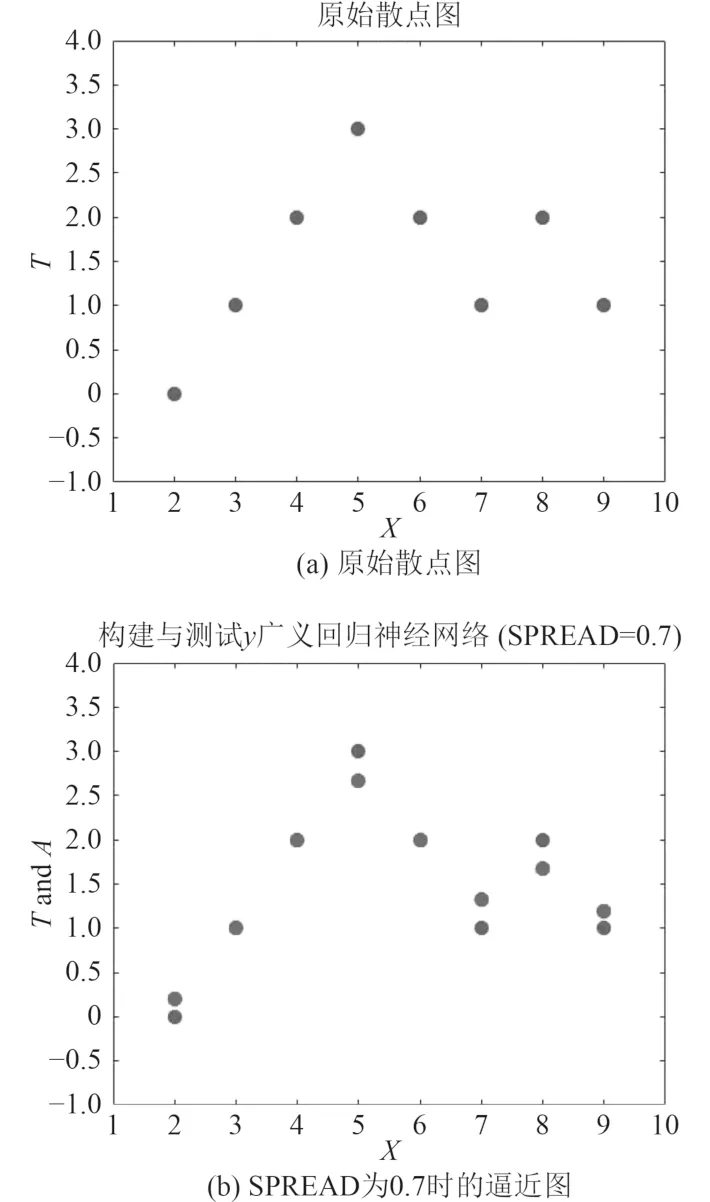
图4 GRNN算法函数逼近拟合仿真图Fig. 4 Simulation of GRNN algorithm function approximation
调节SPREAD值为0.5,每次向小调节0.1,可得仿真图如图5所示。
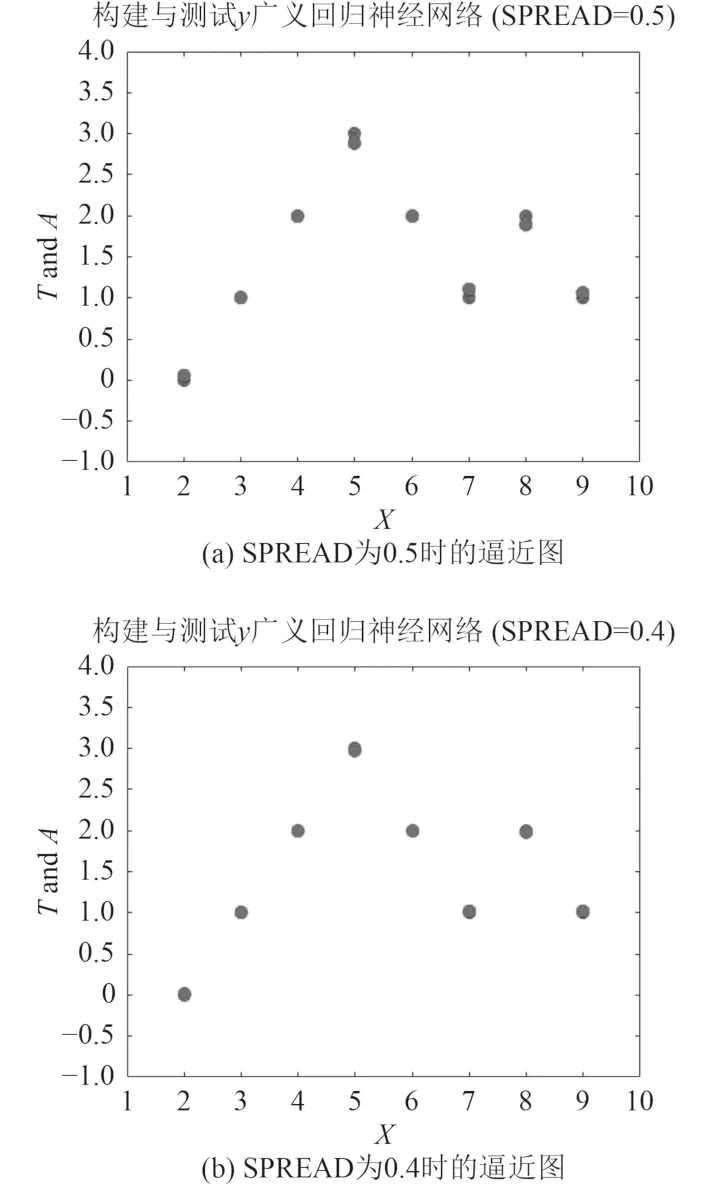
图5 改变SPREAD值的逼近对比图Fig. 5 Approximation comparison chart of changing spread value
由图5可见,通过调节SPREAD值,优点是较小的SPREAD值能更好地拟合数据,缺点是越契合原始数据点,所得到的曲线不太平滑(折线),当调整取得一个合适较小的SPREAD值时,GRNN算法所拟合的数据点可完全和原始数据点契合。
进一步的可通过网络求得相关所需点(缺失数据的离散点),这些点与原始数据在很大程度上契合,可由此认定为真值。同样的仿真过程求缺失点数据,当取SPREAD值为0.2时,如图6(a)所示,GRNN神经网络已经完全逼近原始数据点,再取输入为任意一个值,如X=4.5,可以得到新的数据点,如图6(b)所示。
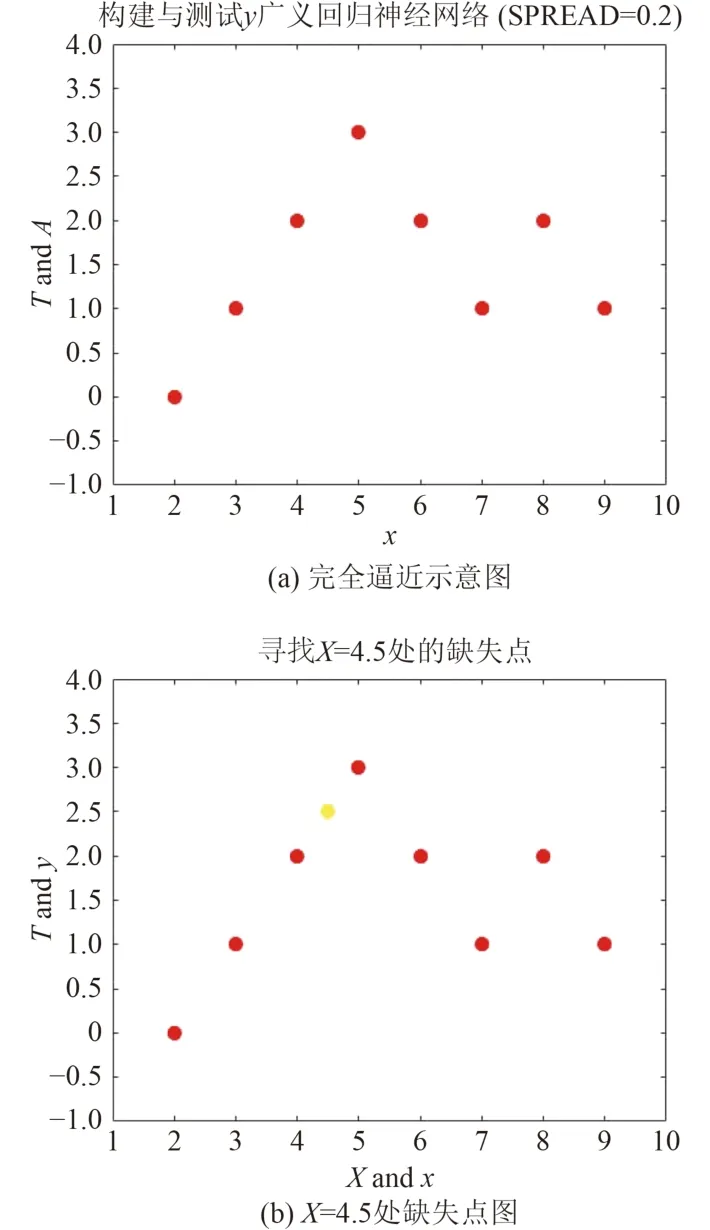
图6 GRNN神经网络寻找缺失数据图Fig. 6 GRNN neural network for missing data
通过以上的仿真过程,确定了GRNN算法用于离散点的逼近的可行性以及用于缺失点寻找的思路和方法。为验证所建立算法的适用性、精度及插值效果,利用MMSI码为412 212 020的船舶在某天出航的试验数据,截取了时长为15 min、时间间隔为30 s的>AIS数据(已经过数据预处理),基于Windows平台,在 Matlab中编程实现L-GRNN算法用于恢复表1中缺失的AIS数据,最后绘制了船舶轨迹散点图。
依据表1,可以绘制出未使用L-GRNN算法处理的经纬度散点图。考虑对AIS数据应用L-GRNN算法,依照前文所叙述的步骤,需要进行插值的时刻以及插值点所得到的值如表2所示。
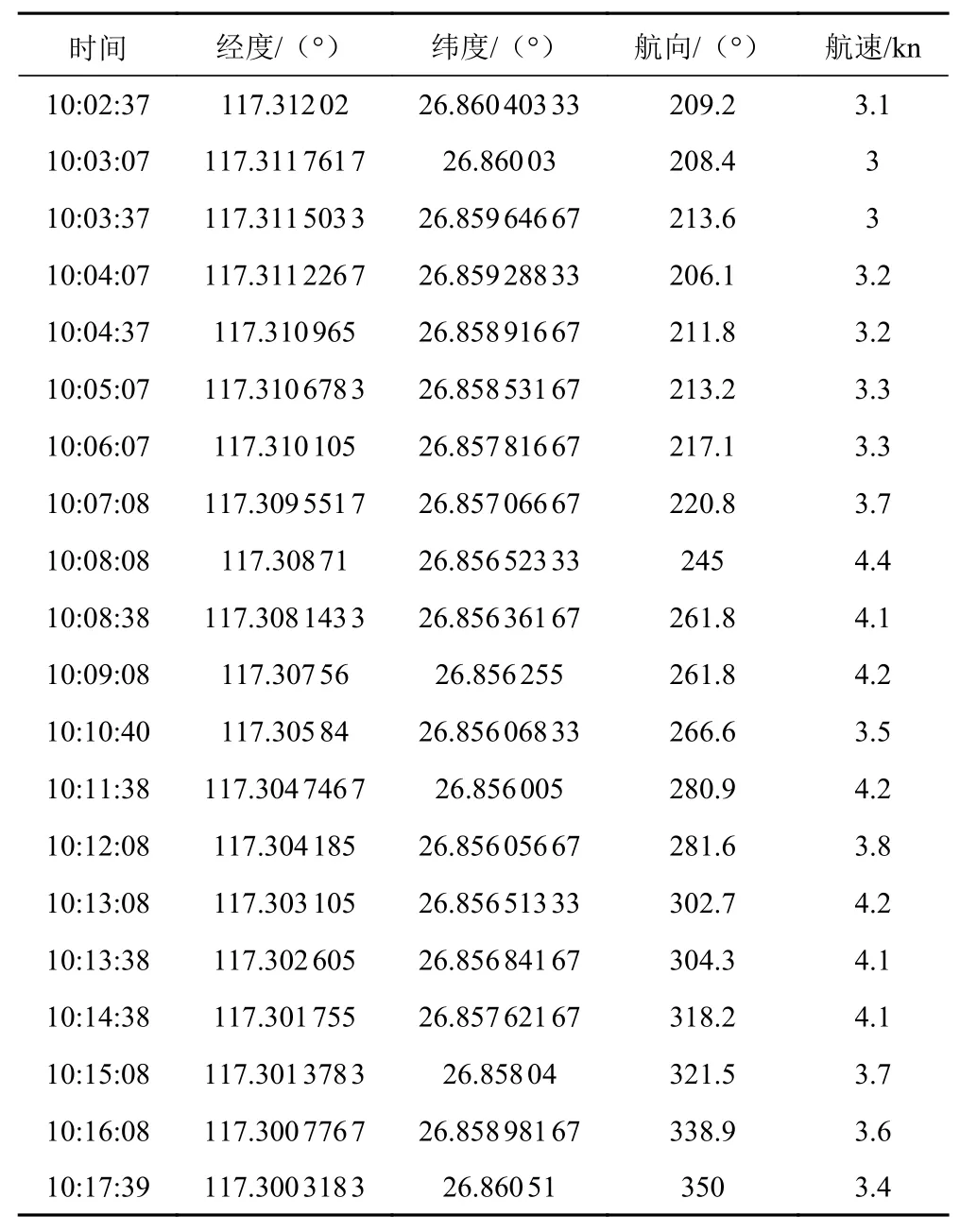
表1 时间先后排列的AIS序列1Tab. 1 time sequenced AIS sequence 1
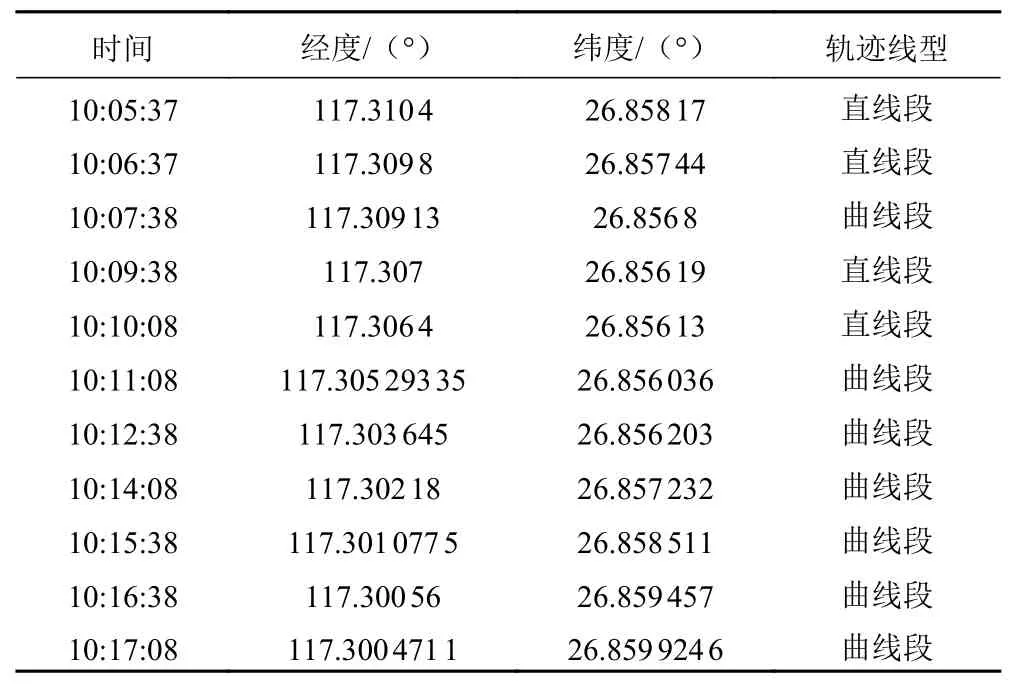
表2 L-GRNN算法进行插值处理的数据表Tab. 2 data table of interpolation processing by L-GRNN algorithm
最后,为验证L-GRNN算法后插值的效果,绘出船舶的轨迹散点图如图7所示。图7(a)为未使用LGRNN算法处理所得的船舶轨迹,图7(b)~图7(e)为使用各插值算法后得到的船舶轨迹散点图。
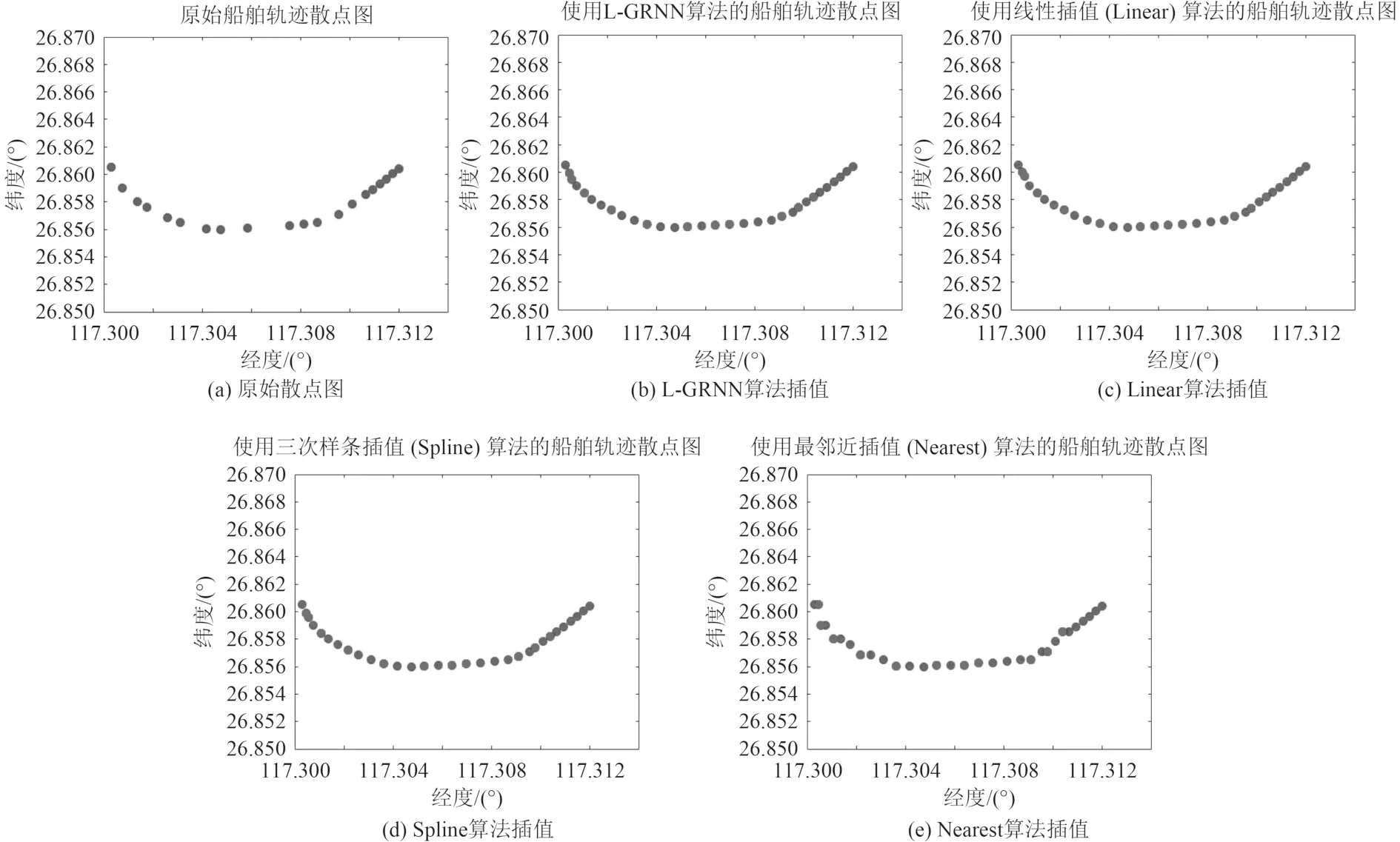
图7 船舶轨迹散点图对比Fig. 7 Comparison of ship trajectory scatter plot
通过以上船舶轨迹散点图的对比,可确定LGRNN算法具备了Linear算法与Spline算法的精度,且进一步观察起始段的缺失点,可发现L-GRNN算法所得到的插值点上下分布均匀即比Linear算法与Spline算法平滑效果更好。
4 结 语
本文提出了一种用于AIS数据插值的L-GRNN算法,通过仿真研究和实船数据验证,验证了该方法的精度、平滑性能较好,且该方法与传统的AIS数据插值方法相比,同时具备了精度、平滑性能,具有良好的工程适用价值。

