分层流中附体对潜航体尾迹频谱特性影响研究

胡开业，杨哲超，于 祥，丁 勇

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

0 引 言

实际海洋流场具有普遍的密度分层现象。一定深度时产生密度跃变的密跃层，跃层厚度较薄时，可视为密度突变的强分层情况。潜艇等水下潜航体在强分层环境中运动的海表特征格外显著，更易被高分辨率合成孔径雷达SAR（Synthetic Aperture Radar）捕捉，进而暴露型号、潜深、航速等信息。因而如何弱化乃至控制潜航体运动诱发内波的表面效应，从而避免高分辨率合成孔径雷达的监测已成为各国海洋军事的研究热点。

二维谱分析法在海洋探测中广泛运用。其得到的功率谱密度图不仅包含时域和频域信息，还可以依据尾迹频谱图的特征差异，分析复杂附体对潜航体尾迹各频率成分的耦合影响。本文首先介绍计算流体力学和快速傅里叶变换的基本理论模型，然后模拟4种潜航体模型在分层流中的运动情况，对比计算工况下的内界面和自由面时域波形图。最后运用二维FFT算法对内界面波和海表面兴波进行频谱分析，探究附体与艇体对内界面和自由面尾迹特征影响的作用规律。

1 理论模型

计算流体力学将连续的物理量场用离散的变量点代替，而二维离散傅里叶变换可将CFD求解的时域离散结果转换到频域。本文以内界面和自由面时域的二维波高信号为输入，经过频谱变换获得不同工况的功率谱密度图。

1.1 数值模拟控制方程

流体流动遵循质量守恒、动量守恒、能量守恒，在模拟计算潜航体运动流场过程中，不计及能量转换。

1）连续方程

在流场域内，无源无汇前提下，单位时间内流体微团的质量改变量，等于单位时间流入或是流出微团的流体的质量。定常、不可压缩的恒密度流体，直角坐标系连续方程如下：

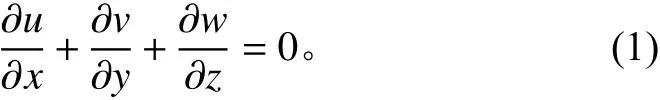
其中：u，v，w是 速度矢量在x，y，z方向的速度分量。

2）动量守恒方程

单位时间内，流体微团动量的变化率，等于流体微团受到的合外力。动量守恒方程如下：

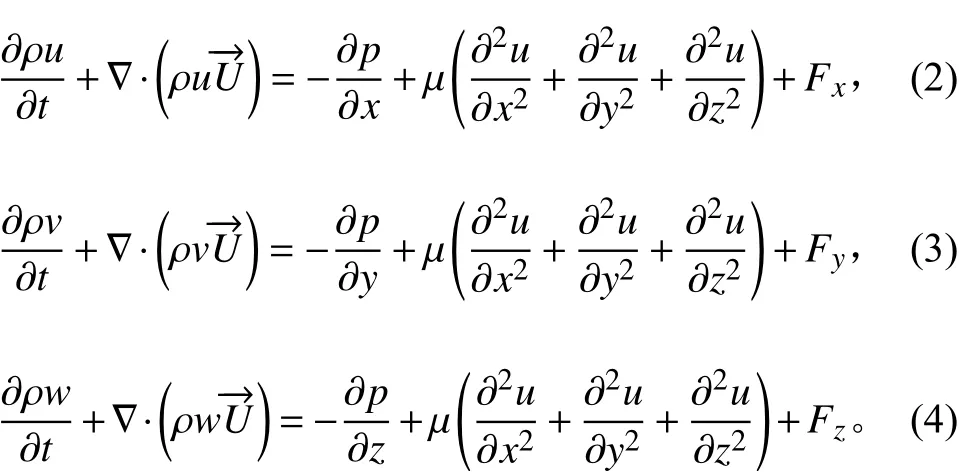
其中：p是流体微团上的压力；u，v，w及Fx，Fy，Fz分别为流体微团在x，y，z方向上的速度和所受到的体积力。

采用VOF法构建流体密度分层模型，精确捕捉内界面和自由面的波动情况。

3）VOF多相流模型

1.2 频谱分析法

1）二维离散傅里叶变换

二维离散傅里叶变换将信号分解成不同频率的基元信号的和，从而表示不同频率分量的分布情况，计算信号的统计特性。用正交系x,y的函数f(x,y)表示CFD计算结果中二维离散平面的波高，将f(x,y)转变成关于x,y的 二维离散信号，沿x,y方 向采样M×N个点,二维离散函数的傅里叶变换为：

2）一维功率谱密度

进行谱估计通常采用周期图算法、相关图算法等，由于表征自由面和内界面的波动情况需要大量数据，因此本文采用了计算较为便捷的周期图法。其功率谱密度表示为：

值得注意的是傅里叶变换后的频率谱并不连续,还需进一步对所得阵列进行坐标系变换,使得傅里叶变换谱的中心移到M×N的中心。为使波高特征表现更为直观，通过算法编程对功率谱矩阵进一步处理，计算图像中心同心等宽环带内的平均功率谱密度，获得功率强度在不同频率下的分布情况。

2 计算模型及网格划分

2.1 计算模型

本研究选取美国国防先进技术研究署DARPA所设计的Suboff潜艇为计算模型，并将原模型各向等尺度放大20倍，以便消除尺度效应，模拟百米级潜航体在分层流中运行的实际情况，图1为Suboff全附体模型三维示意图。放大前后主尺度对比如表1所示。放大后艇体总长为87.12 m，艇径为10.16 m，进流段长度为20.32 m，平行中体长度为44.58 m，去流段长度为22.22 m，指挥台围壳高为4.02 m。

图1 Suboff几何模型三维视图Fig. 1 Geometric model 3D view of the Suboff

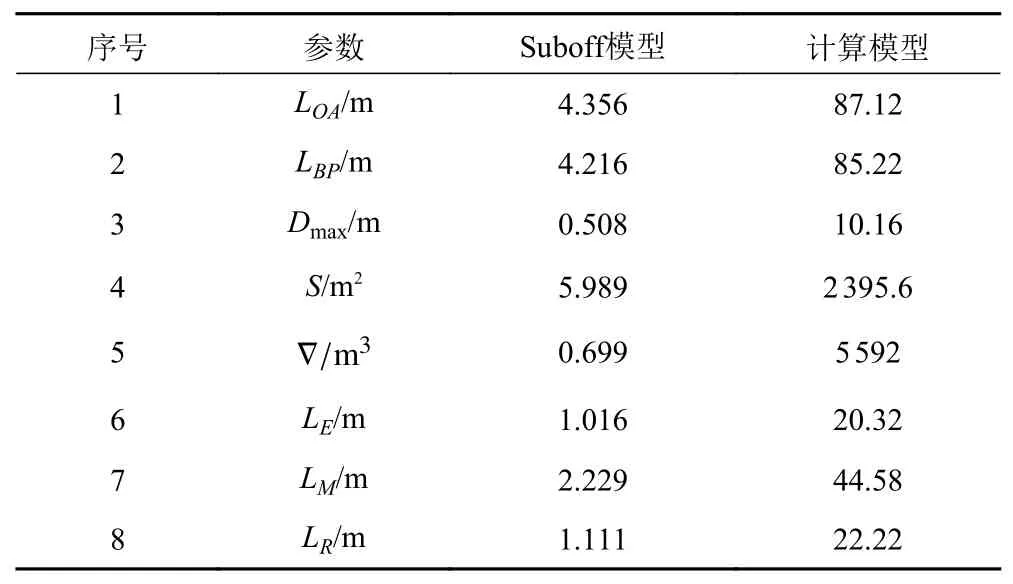
表1 Suboff模型及计算潜艇主尺度Tab. 1 Main particulars of the Suboff

潜航体在水下航行时，航速、潜深以及相对分层界面的位置对潜航体内界面和海表面的几何形态有较大影响。实际作业过程中，航速减小或潜深增大，使得潜航体对自由面的扰动迅速减弱。不同海域在不同时节分层模式也不同，潜航体离内界面越近对内界面的扰动也越明显。本文数值模拟计算时，密度分界面位于自由面以下40 m处，内界面上层流体密度取淡水密度997.56 kg/m3，下层流体取海水密度1 024.2 kg/m3，潜航体航速为20 kn，潜深20 m。为探究潜航体附体在潜航体运行过程中对尾迹的影响，本文将全附体模型又分为光艇（不含附体）、光艇+指挥台、光艇+尾舵3种计算模型，如图2所示，不同计算工况的航速、潜深、分层模式等条件保持一致。

图2 光艇、光艇+尾舵、光艇+指挥台模型Fig. 2 Model of bare hull, bare hull + stern rudder,bare hull + sail, fully-appended hull

2.2 计算域网格划分

计算域采用右手直角坐标系，原点位于潜航体首端中心位置，X轴的负方向为潜航体运动的方向，潜航体右侧为Y轴正方向，Z轴垂直向上。计算域取艇首前方500 m处至艇尾后方1 500 m处，总长2 000 m。为简化计算，取艇体纵向中轴线为对称轴，纵向中轴线右侧宽度取500 m，则计算域总侧向宽度为1 000 m。上方空气高度为20 m，轻流体深度40 m，重流体深度60 m，总水深100 m，则计算域总高度为120 m。数值模拟的计算精度与网格的划分密切相关，本文4个工况下计算域网格数约为2 000万左右，对艇体周围流场、附体、内界面和自由面进一步加密，全附体艇周局部网格划分示意图如图3所示，计算域整体网格划分示意图如图4所示。

图3 全附体艇周局部网格Fig. 3 Local mesh around fully-appended hull

图4 计算域流场网格划分Fig. 4 Mesh generation of computational domain

3 模拟结果及分析

3.1 内界面

图5 为4种不同的艇型在速度为20 kn，潜深20 m的强分层流场中，t=60 s时的内界面波形图，相同航行条件下不同的艇型对内界面的扰动如图5所示。随着潜艇开始运动，艇周流体因艇体体积排挤效离开平衡位置，本研究艇体位于内界面上，这种扰动迅速传至内界面后，在艇首对应位置出现明显的波谷，艇体尺度范围对应位置出现波谷，艇尾向后至较远的位置具有明显的窄V字型波峰。内界面波动的纵向传播范围较横向更为显著，波动主要为散波，几乎未出现明显的横波，波动总体角度约为7°。

进一步可以看出不同的潜航体模型在相同的航行条件下，内界面波的相对位置没有太大差别，但波动参数发生了较大变化，图5（c）为光艇+指挥台在分层流中运动内界面波形图，在60 s时内界面上的最大峰值约为0.257 7 m，相较其他工况具有最峰值最大，图5（d）为全附体在分层流中运动内界面波形图，在60 s时内界面具有最小波峰，相较图5（c）差值约为0.02 m，图5（d）中计算域最大波谷为0.674 1 m 相较其他工况波谷值最大，图5（c）中内界面的最大波谷为0.667 1 m，相较图5（d）差值约为0.007 m。

图5 内界面波形图Fig. 5 Interface wave patter

3.2 自由面

图6 为4种潜航体模型在航行20 kn和潜深20 m时，第60s的自由面波形图。从总体来看，潜航体开始运动后，海表流体受到潜航体体积向上排挤效应，艇体上方向上隆起和艇体尺度相当范围的水丘，又称“伯努利水丘”，水丘的尺度较大、范围较广，水丘引起的自由面扰动向后方发展演化，形成艇体运动后方的自由面波动，最终使得潜航体在航行时引起显著的自由面波动，对潜航体隐身性能有较大的限制。散波和横波的扩散在自由表面均较为明显，散波的波形角约为40°，横波约7个完整波形，自由表面波动场沿艇尾方向传播约600 m。

图6 分别为光艇、光艇+尾舵、光艇+指挥台、全附体潜航体在分层流中运动时自由表面的波形图，对应最大波峰（m）和最大波谷（m）分别为（0.282 9，0.613 6），（0.286 2，0.614 4），（0.311 6，0.683 5）和（0.313 7，0.674 2），对应波高分别为0.896 5 m，0.900 6 m，0.995 1 m和0.987 9 m。由上述数据易知，最大波峰差为全附体潜航体和光艇波峰差约为0.03 m，最大波谷为光艇+指挥台和光艇波谷差约为0.07 m，可知附体的存在对波峰和波谷的影响较大，尤其是指挥台的存在对自由面的波峰和波谷都有显著的影响。自由面的最大波峰最大波高差为光艇和光艇+指挥台波高差约为0.1 m。当潜航体只有指挥台时，会使得潜航体在自由面产生更明显的扰动，只有尾舵相较光艇对自由面的扰动变化增幅较小，但同时具有附体和指挥台时，相较只有指挥台的情况自由面的扰动有所减弱，说明尾舵的流场和指挥台的流场能发生有利的相互干扰。

图6 自由面波形图Fig. 6 Free surface wave pattern

3.3 频谱分析

本研究通过信号处理技术以频率与功率谱密度的关系为特征，进一步分析了潜航体的形态因子、与潜航体内界面和自由表面扰动的波谱特征进行了比较。

将采集的内界面和自由面的波高信息导入信号处理软件进行后处理，在计算潜航体运动仿真时，边界条件中未包括海浪的影响，因此无需对波高信号进行滤波操作。采样频率为f s=1/dt，其中dt为采样时间间隔，它是采样频率的决定性因素。也就是说，它需要在固定的时间间隔内捕获信号并进行功率谱分析。在本研究中速度为固定值，因此在固定时间dt内取样可以转换为在固定距离dx处进行采样即fs=v/dx。采样范围纵向为艇首前50 m至艇尾550 m，横向为艇体左侧300 m至右侧300 m的正方形区域内，采样范围覆盖了整个潜航体的内界面和自由面扰动区域。由于配置附体使得内界面和自由面的波型具有差异，因而对功率谱密度值影响显著，在实际检测过程中，可以通过雷达检测的功率谱密度值的大小从而反演出潜航体附体情况，即可进一步通过波形确定水下潜航体的型号。

图7 和图8分别为光艇在强分层流扰动内界面和自由面后在采样区域内所测得尾迹的功率谱密度图。对比的自由面和内界面功率谱密度图易知，自由表面扰动的波频相较内界面频带范围更广，内界面功率谱密度主要集中在低频带，而潜航体在自由面则产生了高频波，出现双峰型波形谱。说明潜航体在该运动参数条件下对自由面的扰动较为显著。

图7 光艇内界面功率谱密度图Fig. 7 Power spectral density of interface of bare hull

图8 光艇自由面功率谱密度图Fig. 8 Power spectral density of free surface of bare hull

图9 分别为光艇+尾舵、光艇+指挥台、全附体潜航体在相同航速、潜深和分层条件下的内界面尾迹功率谱密度与光艇的内界面尾迹功率谱密度对应频率的差值图。由图可知不同潜航体模型对应频率下内界面的功率谱密度值影响差异较大，但不同艇型的内界面频带延伸范围差距不大，图8的频带范围约为0～0.2之间，图9差值范围未在高频段出现明显的幅值，即附体对采样区域内的内界面的频率分布范围影响不显著。由图9（a）可知只有尾舵的情况对内界面的扰动相较光艇内界面的扰动情况，在高频段没有显著增大的前提下，低频段功率谱密度值具有较大幅度的减少，因此装有尾舵对潜艇对内界面的扰动有较好的优化效果。图9（b）为只有指挥台的情况，对内界面的扰动相较只有光艇时功率谱密度有大幅度的增长，但如图9（c）所示，当同时存在指挥台和尾舵时，潜艇对内界面的干扰相较只有指挥台有所减小，因此尾舵的研究对内界面的尾迹控制具有较大意义。

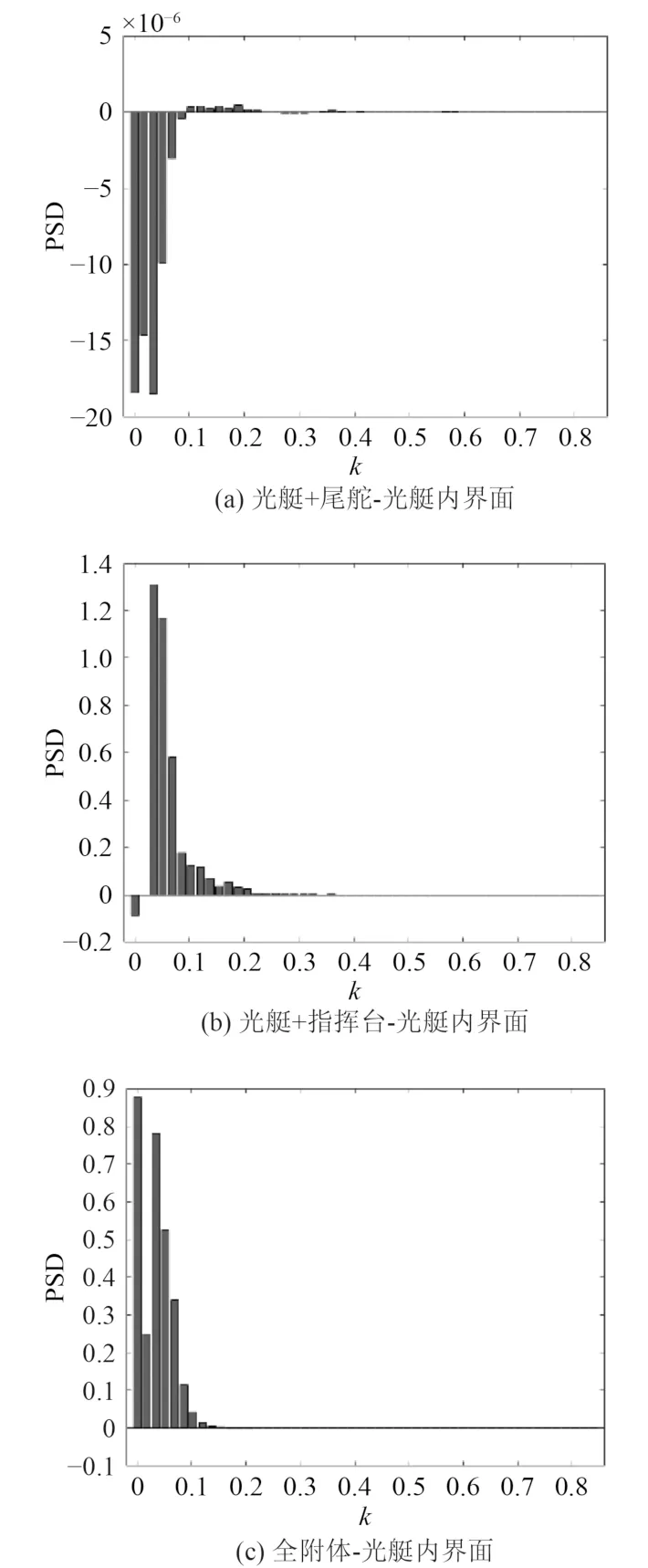
图9 内界面功率谱密度差值图Fig. 9 Power spectral density deviation of of interface

图10 分别为光艇+尾舵、光艇+指挥台、全附体潜航体在相同航速、潜深和分层条件下的自由面尾迹功率谱密度与光艇的内界面尾迹功率谱密度对应频率的差值图。图9频率分布范围小于0.4 Hz，图10在频率值大于0.4 Hz的范围仍有明显的差值,表明附体对自由面的频率分布范围有所影响，其中指挥台占主要影响。由图10（a）可知相较光艇，只有尾舵的情况对低频区的功率谱密度值有较好的改善，对高频区的功率谱值有所增加。对于只有指挥台的情况如图10（b）所示，功率谱密度在整个频带上都有很大增幅，由图10（c）可见同时具有指挥台和尾舵的全附体，高频区的功率谱密度相较只有指挥台的情况略有增大，但低频区的功率谱密度幅值有所改善。

图10 自由面功率谱密度差值图Fig. 10 Power spectral density deviation of of free surface

4 结 语

本文基于粘流理论的CFD方法模拟了潜艇的运动情况，并结合信号处理的二维功率谱密度分析法表征内界面和自由面的表面特性，研究了附体对内界面和自由面影响，相较用波高等尺等参数表征表面特性具有众多优点,功率谱密度分析法能分析用尺等参数无法表示的频率分布等特性，在圆对称的前提条件下进行降维处理后，形式更为简洁直观，更易辨识。本文计算具有较高的精度，为建立对特定几何形状的水下物体的追踪和定位方法及潜艇设计和优化提供新的思路，并为分析潜艇隐身性和反潜SAR遥感研究提供参考。