基于X-ray CT技术和有限元方法的沥青混合料剪应力计算分析*
常艳婷,田 丰,陈忠达 ,Lizhi Sun
(1 西安铁路职业技术学院,陕西西安710026;2 中国市政工程中南设计研究总院有限公司,湖北武汉430010;3 长安大学 特殊地区公路工程教育部重点实验室,陕西西安710064;4 加州大学尔湾分校 土木与环境工程学院, 加州尔湾92697)
沥青混合料是由集料、沥青胶浆及空隙三种成分组成的非均质混合物,在荷载作用下,混合料内部的应力分布呈现非均匀性。而目前国内外的道路设计理论均将路面处理成连续均质体系,但采用连续介质力学方法研究具有非连续性特征的道路材料,难以真实地模拟其受力、变形及破坏过程。因此,部分学者开始对该非均匀性进行研究,如:万成等[1]通过获取三维细观结构并建立三维数值试样,对试样受荷载作用下的拉应力集中因子进行了研究,得出三维数值试样内部的应力和应变分布均呈现不均匀状态,空隙的存在显著增加了试样受荷载作用下的应力集中;李智[2]通过编写MATLAB程序将各组分空间分布信息导入ABAQUS平台中,实现混合料数值芯样重构,并最终对低温弹性体的有限元抗压力学模型进行了抗压力学分析,得出截面抗压应力均值和应力分量不均匀系数可有效评价芯样的质量不均匀性;王端宜等[3]利用CT扫描图像,结合有限元建模方法,模拟沥青混合料劈裂试验对混合料内部拉应力的不均匀分布进行了研究,得出采用DIP-FEM方法能够很好地将沥青混合料的微观结构和宏观力学性能结合起来。然而国内外已有大部分研究,在三维数值模型重构方面仍然采用先利用AVIZO等软件进行CT图像识别与处理,再编写程序将组分信息导入有限元软件中,该过程较为复杂[4]。本文采用的Simpleware软件可提供各种格式(DICOM、Raw image data等)原始图像CT、MRI等的可视化、图像处理、图像分割,并采用独特技术划分出合理的网格,并可同时进行网格质量检测及修复错误,生成的网格模型可直接导入商业FE(如ABAQUS、ANSYS等)、CFD或CAD软件中,实现了三维数值模型重构的便利性。而且本文采用的CT扫描设备能够区分出细集料与沥青胶浆(沥青与矿粉),克服了以往将胶浆与细集料笼统归结为沥青砂胶而给计算带来的不准确性。同时可以看出,已有研究多利用混合料细观结构三维数值试样进行拉、压应力计算研究,而针对剪应力计算并将其与宏观抗剪性能联系起来的研究尚显不足。而沥青路面在水平荷载与竖向荷载的综合作用下产生较大的剪应力,当混合料抗剪强度不足时,极易产生车辙、推移、拥包等剪切破坏。因此,本文采用nano-CT扫描设备对所制备的芯样进行扫描,然后采用Simpleware软件对CT图像进行图像处理,生成网格模型,并将其导入ABAQUS软件中,进行混合料剪应力的计算,并分析温度对最大剪应力值的影响,最后将计算结果与宏观抗剪性能联系起来。
1 试验
1.1 材料
本文所采用的AC-13沥青混合料级配见表1,胶结料采用SK-90#沥青,集料及矿粉均为石灰岩,沥青混合料的最佳油石比为4.82%。

表1 沥青混合料级配Table 1 Gradation of asphalt mixture
1.2 试件制作
Nano-CT扫描设备对试件的最大尺寸要求较严格,为了提高扫描图像的清晰度,首先成型标准马歇尔试件,然后采用20mm钻头进行钻芯,并进行切割,形成20mm×20mm的圆柱体芯样,用于CT扫描试验。
1.3 X-ray CT 扫描
CT设备采用准直后的X射线束对试件进行扫描,衰减后的X射线由探测器接收并被转换为可见光,再由光电转换器转变为电信号,最后经数字转换器(Digital Converter)转换为数字信号,输入计算机进行处理并显示CT图像[5]。不同物质对X射线吸收能力不同,物质密度越大、组成物质的原子序数越高,对X射线的吸收能力越强[6]。集料、胶浆及空隙之间密度差别较显著,使得三组分较易在CT图像中进行区分,其扫描原理如图1所示。

图1 CT扫描工作原理Fig.1 Working principle of CT scanning
本文采用加利福尼亚大学尔湾分校土木与环境工程学院的VersaXRM-410纳米CT设备对沥青混合料芯样进行层析扫描,经X射线CT设备所采集的沥青混合料内部结构如图2所示。

图2 沥青混合料的二维及三维CT图像Fig.2 2D and 3D CT images of asphalt mixture
2 沥青混合料三维数值模型重构及有限元计算
沥青混合料三维数值模型重构及有限元计算过程如下:
(1)对所采集的1004张沥青混合料水平截面进行异常截面剔除,将剩余的850张CT图像导入Simpleware图像处理软件中,进行Resample、Crop等操作以实现图像分辨率调整及切割。利用集料、胶浆及空隙三相的灰度值不同这一特点,采用最大类间方差法[7](大津法,OTSU)进行混合料三组分区分,处理结果如图3所示,图中的紫色、绿色及白色区域分别代表集料、胶浆及空隙,由图可知,混合料中的三组分被较好地区分出来。
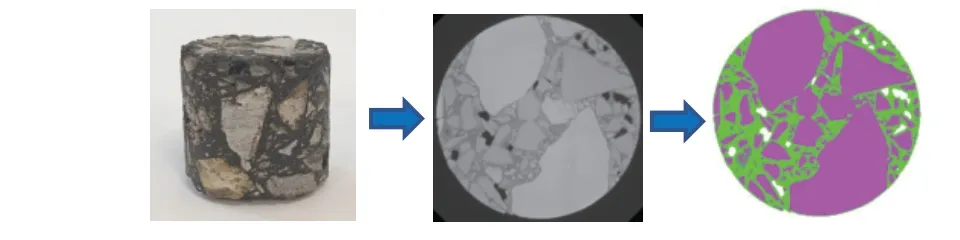
图3 Otsu法处理结果Fig.3 Results of Otsu method
(2)经试验发现,直接对圆柱体芯样进行网格划分所得到的单元数量庞大,使得有限元计算较为困难,因此采用Crop功能对芯样进行切割,同时为了提高计算结果的准确性,分别在芯样的不同部位截取2mm×2mm ×2mm的立方体,共形成10个立方体。
(3)通过Simpleware软件的创建模型模块进行有限元模型创建,并对网格划分参数进行设置:为了使所划分出的网格更合理、美观、利于计算,采用FE Grid网格划分算法,即网格划分粗糙度为0;同时,为了利于计算结果收敛,采用六面体/四面体线性减缩单元。其中一个立方体三维图像及其对应的网格划分结果如图4所示。

图4 网格划分结果示意图Fig.4 Schematic diagram of grid generation results
(4)将各立方体的网格划分结果进行输出,形成INP文件,然后将该INP文件导入ABAQUS软件中进行计算,如图5所示。为了研究沥青混合料内部应力的不均匀分布,对集料单元、沥青胶浆单元及空隙分别赋予不同的材料参数,其中集料模量取为50000MPa,泊松比为0.25;为避免计算错误,空隙模量采用0.5MPa,该取值对整体计算结果的影响可以忽略[8]。胶浆的力学性质受温度的影响较为显著,反映为其模量随温度的升高而减小。本文为了计算的简便,将20℃、30℃、60℃条件下的胶浆模量取为220MPa、150MPa及30MPa。

图5 INP文件导入示意图Fig.5 INP file import diagram
(5)模拟中对上表面施加均布位移荷载,下表面的边界控制条件为U2=UR1=UR3=0,然后计算不同温度条件下,即不同胶浆模量条件下的沥青混合料最大剪应力值。
3 最大剪应力计算结果
图6为剪应力发展情况云图。
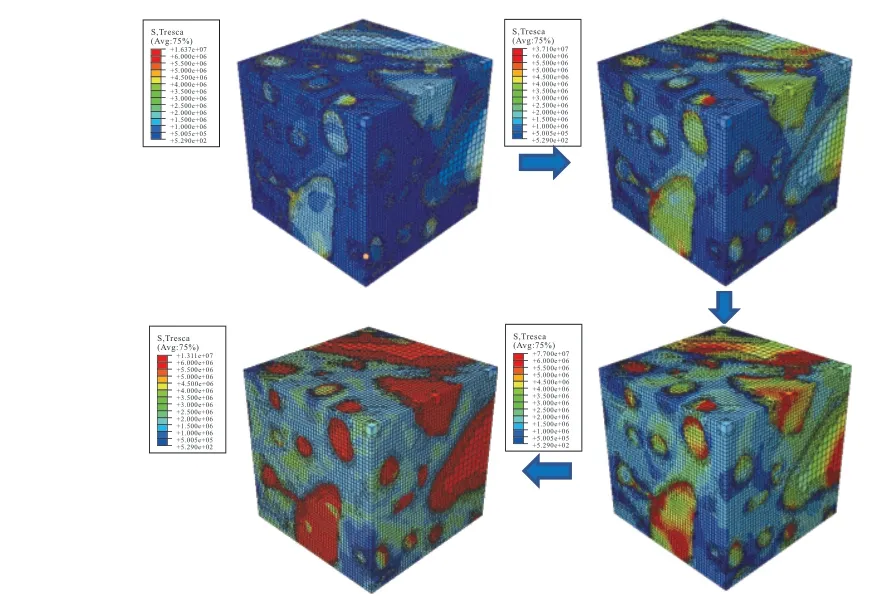
图6 剪应力发展过程Fig.6 Development process of shear stress
由图6可知,加载初期剪应力较小且首先出现集料及胶浆与集料结合部位,随着荷载的增大,集料承担的剪应力逐渐增大,而胶浆所承担的剪应力则始终较小。当剪应力较大时,剪切破坏极易于混合料的薄弱部位,即集料、胶浆的结合处产生,计算结果与实际情况相符。而且已有研究表明,集料的棱角性及取向等特征是控制混合料抗剪性能的重要因素,因此,研究集料结构并进行结构优化设计能够显著提高沥青路面的抗剪性能。
按照前述步骤分别对取自不同部位的10个立方体进行三维数值模型重构及有限元计算,得到各立方体在不同温度条件下的最大剪应力值,见表2。

表2 最大剪应力值(MPa)Table 2 Maximum shear stress
由表2的计算结果可知,各立方体的最大剪应力值均随温度的升高而增大。由于各立方体中三组分的分布及所占比例等均不同,如2、4、6、8、10号立方体中集料所占比例分别为53.9%、45.7%、33.0%、74.7%、44.3%,因此,计算结果存在差异,最大剪应力值随着温度的变化幅度也不同,当温度由20℃升高至60℃时,最大剪应力值的增大范围为2.99%~8.73%。由此可见,当温度升高时,最大剪应力随着集料与胶浆模量比的增大而增大,表明沥青混合料在高温条件下更易发生剪切破坏。
4 计算结果合理性验证
为了验证计算结果的合理性,本文采用同济大学毕玉峰等提出的单轴贯入试验测定沥青混合料在20℃、30℃ 、60℃条件下的抗剪强度[9]。该试验与三轴试验相比,试件中的剪应力分布与实际路面中的剪应力分布更相符,且试验方法简单,其示意图如图6所示。试验结果见表3,其中抗剪强度由贯入应力均值乘以抗剪强度系数(0.339)所得。
图6 单轴贯入试验示意图Fig.6 Schematic diagram of uniaxial penetration test
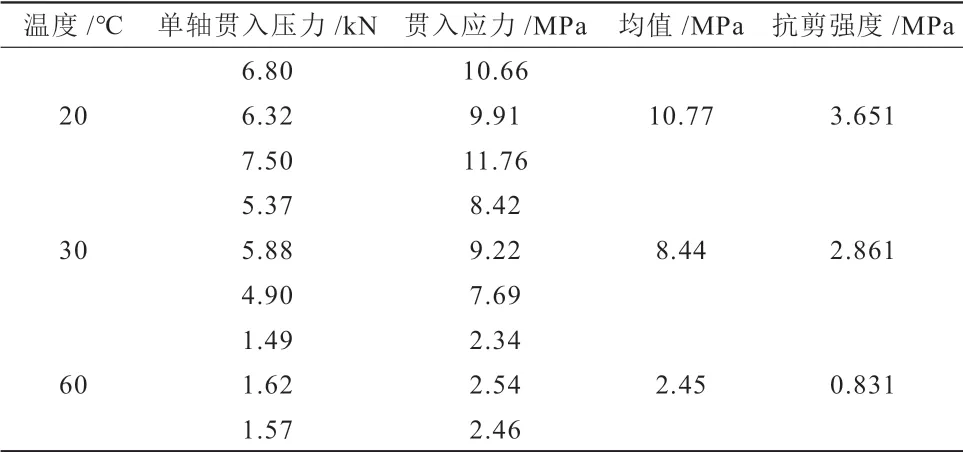
表3 单轴贯入试验结果Table 3 Results of uniaxial penetration test
由表3可知沥青混合料的抗剪强度随温度的升高而降低。因此,在同一荷载作用下,沥青路面在高温条件下更易发生剪切破坏,这与前述有限元计算结果所揭示的现象一致,即验证了该计算结果的合理性。
5 结语
(1)三维数值试样内部的剪应力分布呈现不均匀性,最大剪应力较大值基本分布在集料及集料与胶浆结合处,而胶浆则基本不承担剪应力,因此,集料在混合料抵抗剪切变形方面具有主要的作用。
(2)最大剪应力值随着温度的升高而增大,表明混合料在高温条件下更易发生剪切破坏,而不同温度条件下的单轴贯入抗剪强度的测定验证了计算结果的合理性。

