基于遗传模拟退火算法的压缩感知重构方法
肖畅,樊晓宇
(1.合肥工业大学 计算机与信息学院,合肥 230601;2.安徽科技学院 电气与电子工程学院,蚌埠 233030)
压缩感知(Compressed Sampling,CS)是一种数据压缩与重构理论,CS对具有稀疏性或在变换域上稀疏的信号在满足特定条件下,可通过远低于奈奎斯特采样定理的随机采样完成原信号的精确重构。这种新颖的压缩与采样同时进行的信号处理方式,能够有效降低信号采样、传输和存储的代价,使信号的处理方式得到一次深刻的变革[1-4]。
CS主要包括三个问题,即信号在某个域上的稀疏变换、观测矩阵的构造和信号重构算法的设计,本文设计的方法是针对信号重构环节进行的。CS的有效信号重构算法诸多,主要包括:直接求解l0范数最小化问题的匹配追踪算法[5]和把l0范数最小化转化为l1范数最小化,通过线性规划求解的基追踪算法[6]。目前出现了一些改进算法,如正交匹配追踪法、梯度追踪法等[7-10]。然而,上述的有些算法需要已知信号的稀疏度,这给应用带来很大不便。刘亚新[11]、高睿[12]、张宗念等人[13]分别提出了信号稀疏度未知条件下的信号重构算法,但是这些算法主要归结于匹配追踪,其缺点是算法需要进行有效的子空间扩充与跟踪,将导致算法需要大量的循环次数才能保证重构信号逼近原信号。朱丰等人[14]研究了运用遗传迭代思想,在稀疏度未知情况下,可准确重构出原信号,避免了子空间跟踪,但遗传算法(Genetic Algorithm,GA)的局部搜索能力较差,这导致了基于单纯遗传算法的压缩感知重构方法具有一定的缺陷。
本文提出一种基于遗传模拟退火算法(Genetic and Simulated Annealing Algorithm,GASA)的CS信号重构方法,它是采用遗传算法和模拟退火算法思想,将CS的信号重构问题等效为生物学中染色体复制、选择与交叉的遗传处理以及模拟退火过程的退火最优化处理,通过不断迭代来逼近最优的信号重构结果,获得稀疏性信号重构结果中各非零元素的位置信息,再使用最小二乘法来计算各非零元素的幅度信息,从而完成信号重构的整个过程。本文将提出的CS信号重构方法应用于基于CS理论的一维信号与二维图像信号重构处理,以考察本文方法的有效性。
1 CS模型
压缩感知的前提是:要求信号满足在某种变换基下是稀疏的或可压缩的,即信号稀疏变换后非零或较大系数的个数远远小于信号本身的非零个数。此时,利用较少的有限系数就可以精确地表示原信号的绝大部分信息。再利用测量矩阵与信号进行乘积,可以获得原始信号在该测量矩阵作用下的投影信息。然后,利用该投影信息结合CS的信号重构算法就可以精确地重构出原始信号。
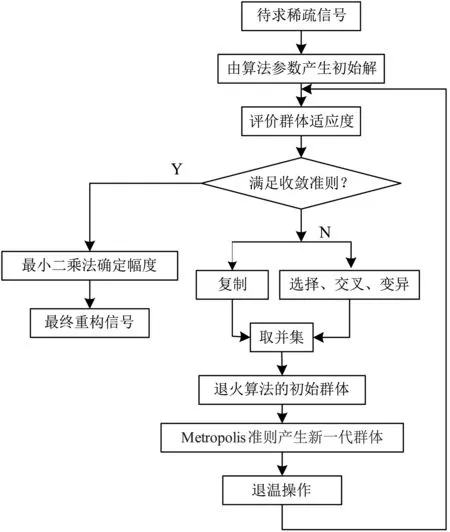
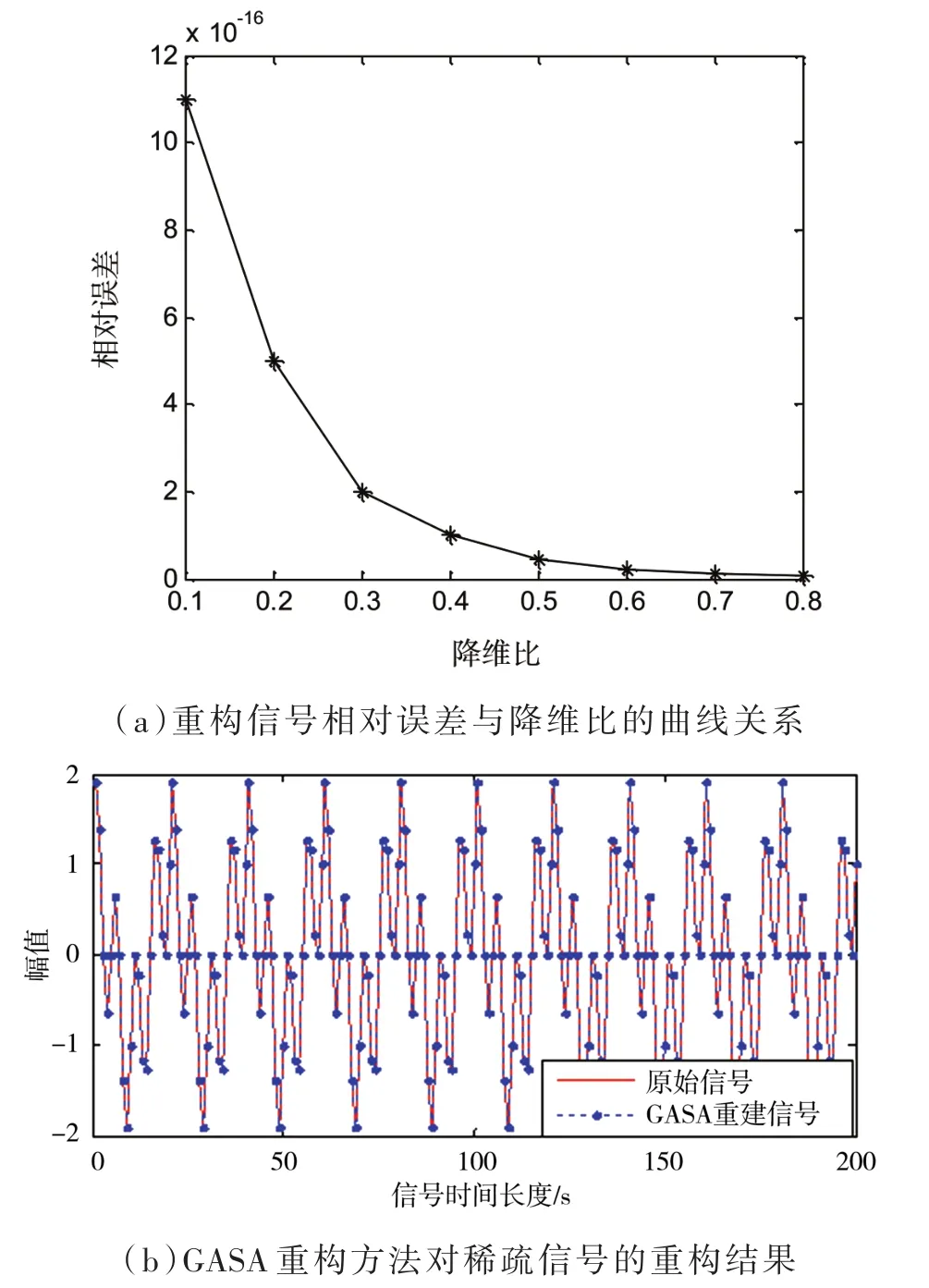
若长度为N的离散实值原信号f∈RN,在某正交基Ψ=[ψ1,ψ2,…,ψN]上是K稀疏的(1≤K< 式中,x是N×1维的投影系数列向量,且仅有K(K< 若信号f满足稀疏性,可采用与Ψ不相关的M×N测量矩阵Φ(M< 式中,y是M×1的观测向量,其元素个数小于等于f元素个数,实现了对信号f的压缩采样。 将式(1)代入式(2),得: 式中,Θ =ΦΨT为CS的信息算子,其列向量称为原子。因测量维数M远小于信号维数N,所以无法直接从y的M个观测值中解出信号f。由于式(3)中x是稀疏的,可通过求解式(3)的逆问题解得x,然后将x代入式(1),求得原信号f。 CS重构问题是在已知测量矩阵Φ及观测向量y的情况下重构出原信号f。用观测值y重构原信号f可通过求解l0范数下的最优化问题来完成,即: 若原始信号f能够以高概率精确重构,则Θ需要具备有限等距性质[15-17]。 GASA是将GA与模拟退火算法(Simulated An‐nealing Algorithm,SA)相融合而构成的一种优化算法。与GA操作过程相似,GASA从随机产生的初始群体进行全局最优解的搜寻,首先通过染色体复制、选择、交叉和变异的遗传操作获得一组新个体,随后再对新个体进行模拟退火操作,将操作结果视为下一代群体的个体。该操作过程进行反复迭代,直到达到终止条件。GASA将GA和SA的优点充分结合,大大提高了算法的效率。 由CS理论可知,由观测值y通过重构算法可求解出稀疏性信号̂,再利用稀疏反变换即可获得原始信号̂。基于GASA的CS信号重构方法是以优化模型的目标函数为起点,将信号的重构过程等效为染色体的复制、选择、交叉和变异等遗传操作,再将遗传操作获得的新个体进行模拟退火最优化操作,通过迭代近似获得信号最优的重构结果,从而得到稀疏结果非零元素的位置信息。然后,使用最小二乘法求解出非零元素的幅度信息[14],整个GASA的CS信号重构过程类似于传统处理方法的反过程。 GASA的CS重构方法是由GA与SA确定CS重构中稀疏表示结果的非零元素位置信息,本文构造的GASA重构方法求解过程的步骤为: (1)设定群体与编码方案。CS重构问题的最优解用数字串表示,每个数字串为一个染色体。结合CS理论,将所求稀疏信号等效为染色体进行群体设定,产生的群体集合表示为。群体初始温度设为 T0。 (2)目标函数定义为: 式中,λ∈(0,1)。最终目标是使目标函数g取得最小值,即求得min{g}。本文使用的适应度函数Fi定义为: 式中,gmax是目标函数g的最大值。每个染色体的适应度值由适应度函数确定,适应度值Fi越大,染色体集合越接近式(4)的最优解,优化目标是寻找参数集合使目标函数g最小。 (3)算法终止条件。通过每代群体最小目标函数gmin的变化来判断算法是否停止。满足设定误差δ,算法收敛,输出最优结果;否则,进行步骤(4)。 (4)复制。设定父代与子代的代沟值GAP,GAP∈(0,1),群体的个体数量L乘以(1-GAP)的值作为最优个体直接复制到下一代的数量,而其他个体由选择操作产生。该过程保留了群体的最优解,算法能够以高概率收敛于全局最优解,使算法具有收敛性。 (5)选择。由适应度函数值进行个体选择,选择方法采用轮盘赌法,最终目标是使目标函数g取得最小值。个体i被选中到下一代的概率为: (6)交叉和变异。设置的交叉概率Pc与变异概率Pm可以动态调节,以克服“早熟”现象,同时达到算法加快搜索速度的效果。Pc与Pm随适应度值自动改变的表达式为: 式中,k1、k2为常系数;gavg为当前群体目标函数的平均值。通常,个体的适应度值小,则具有较大的Pc和Pm,能够加快算法搜寻速度。若GA取得局部极值,适应度值较大个体的Pc、Pm也将增大,能够避免“早熟”现象。当|gmin-gavg|<ε时,固定Pc、Pm值,以避免原解空间被破坏,ε为任意小的数,且ε>0。 交叉操作是以交叉概率Pc进行单点交叉,产生两个新个体。变异操作是以变异概率Pm进行基本位变异,产生新一代个体。通过由选择、交叉和变异操作获得的个体,利用回溯思想,将它们与复制操作直接复制到下一代的个体进行合并,然后再进行步骤(7)。 (7)确定初温及退温操作。 退火函数定义为: 式中,n为GA的第n次迭代;α为温度调节系数,取值范围为(0,1);温度T由初始温度缓慢降到0。 (8)接受退火操作产生的个体。将GA操作产生的群体作为退火操作的初始群体,利用Metropolis准则产生下一代群体。在个体i的邻域中随机产生新个体j,i和j竞争进入下一代群体的准则是:令 ΔF=Fj-Fi,若 ΔF>0,新个体 j优于原个体i,则接受新个体j;若ΔF≤0,原个体i优于新个体j,要先用式(11)计算概率P,然后进行判断。 式中,Tn为第n迭代的温度。然后再产生[0,1]间的随机数r,若P>r,则新个体j被接受;否则,i被接受,j被抛弃。Metropolis准则保证了群体多样性,避免陷入局部最优解。 综上一系列操作,通过反复迭代就可收敛到最优染色体,即为最优解。方法获得的最优染色体由0或1组成,其中1为信号稀疏表示的非零元素,其位置信息对应信号稀疏表示的非零元素位置。 利用最小二乘法在信号稀疏表示的非零元素位置进行投影来确定幅度信息[14]。若信号稀疏表示的第l位是非零元素,则该非零位置的幅度为: 式中,Θ为恢复矩阵;Θl为Θ =ΦΨ的第l列;<·>为内积运算。由该计算可得稀疏表示的各非零元素幅度信息。 GASA的CS重构方法流程为: (1)初始化:L个随机产生的染色体作为初始群体Z(0), (4)设定代沟值 GAP,GAP∈(0,1);将 L(1-GAP)个最优个体复制到下一代,构成集合x̂1; (5)将(3)中的其他个体i按照式(7)以概率Pi选择,选择的个体i遗传到下一代; (6)设置系数 k1、k2值,并分别按式(8)和式(9)计 算 Pc和 Pm。 若 gavg→gmin,Pc、Pm增 大 ;若,固定 Pc、Pm,ε 为任意小,且 ε>0。然后分别以Pc、Pm对步骤(5)选择操作获得的个体进行交叉和变异,构成集合x̂2; (8)退火操作 Tn= αTn-1,α∈(0,1);得到新群体Z(n+1); (9)计算 Z(n+1)的目标函数值,令 s=gmin;判断s (10)设置 q、δ值,n ≥ q时,若 s*在 δ范围内,满足终止条件,则以s*为最终解输出,算法结束;否则,返回步骤(3); 该算法的流程图如图1所示。 图1 GASA的CS重构方法流程图 采用GASA的CS重构方法对长度为N=200的稀疏信号进行重构,观测值数目M=100,L=20,G=0.15,k1=0.7,k2=0.05,q=50。最终各原子是以GASA重构方法最优解s*串的“1”所在位置从字典中选取的,然后进行各原子的线性组合重构出原信号。原信号与重构信号分别用f与̂表示,相对误差Em定义为: 若Em值越小,则表示重构方法的优化能力越好,信号重构的精确越高。 利用GASA重构方法对原信号重构的相对误差随着降维比的增大而迅速下降,如图2(a)所示。由图2(a)可知,当信号的降维比大于10%时,GASA重构方法的重构信号与原信号相对误差很小,其值小于10-15数量级,该方法能够对原信号进行精确重构。信号降维比为10%时,采用GASA的CS重构方法信号重构的实验结果如图2(b)所示,由图2(b)可知重构信号与原信号误差很小。实验证实了GASA的CS重构方法对稀疏信号的重构精度高、效果好。 图2 GASA的CS重构方法对稀疏信号的重构效果 实验图像为四幅512×512的自然图像Pep‐pers和 Lena、核磁(Magnetic Resonance,MR)图像Brain和foot[18]。每幅图像在含高斯白噪声情况下,利用GASA的CS重构方法进行MATLAB实验,获得每幅图像的PSNR及图像重构视觉效果。实验中,L=30,G=0.1,k1=0.85,k2=0.05,q=40,ε=δ=0.01,算法的迭代次数m=100。每幅自然图像都利用小波基db3为正交基矩阵,其投影的测量值为y;每幅MR图像经傅里叶变换后在采样率为10%的2D变密度随机采样[19]下的测量值为y。四幅图像使用GASA的CS重构方法,图像重构结果的PSNR值分别为31.26 dB、32.64 dB、33.12 dB和32.87 dB,图像重构结果如图3所示。图3(a)-图3(d)分别为原始的Peppers、Lena、Brain和foot图像,图3(e)-图3(h)分别为GASA的CS重构方法图像重构的结果。由图3可见,GASA的CS重构方法能够重构出自然图像和MR图像,在保持图像的结构细节信息和边缘轮廓方面具有一定的优越性。实验表明,GASA的CS重构方法在GA中融入模拟退火和回溯过程后,获得了较高的图像重构PSNR值以及较好的图像重构视觉效果。实验证实了GASA的CS重构方法对自然图像和MR图像重构的有效性。 图3 GASA重构方法的图像重构效果 为了测试GASA的CS重构方法的图像重构精度和方法的全局搜索性能,本文以512×512的Lena与Brain图像为例,比较GA的CS重构方法、基于卡通-纹理分解(Cartoon-texture decomposi‐tion,CD)的CS重构方法[1]、GASA的CS重构方法重构图像的相对误差Em,其中,基于CD的CS重构方法用于自然图像重构时,对文献[1]的图像重构模型进行了相应变化。 对Lena与Brain图像采用GA、CD和GASA的CS重构方法进行的图像重构实验中,Lena图像利用小波基db3为正交基矩阵,Brain图像经傅里叶变换后利用采样率为5%的伪射线采样[19],其不同迭代次数的相对误差Em的实验结果如图4所示。 图4 三种图像重构方法的相对误差曲线图 由图 4(a)、图 4(b)可知,Lena和 Brain图像采用GA、CD的CS重构方法获得重构图像的相对误差较大,GASA的CS重构方法获得重构图像的相对误差较小,即GASA的CS重构方法相比GA、CD的CS重构方法图像重构的精度较高。图4(a)、图 4(b)中,Lena和Brain图像利用GASA的CS重构方法相比GA的CS重构方法达到算法收敛时,迭代次数较少,即该方法的收敛速度较快。这是因为在图像重构时,GASA的运算融合了SA,避免了GA的局部搜索能力差及“早熟”现象。从理论分析和实验都证实了GASA的CS重构方法相对GA的CS重构方法图像重构的精度较高,迭代次数较少。然而,GASA的CS重构方法相比CD的CS重构方法图像重构达到收敛时,迭代次数较大。这是因为GASA方法中的GA与SA算法在图像重构过程的收敛速度与CD的CS重构方法相比较慢。 GASA的CS重构方法能够增强搜索全局和局部最优解的能力,将其应用于一维信号和二维图像的重构,实验结果表明在合适的参数下,该方法能够精确地重构出原信号,具有较好的图像重构质量和效果。同时,该方法的收敛迭代次数较小,能够提高整个方法的运算效率。GASA的CS重构方法融合了遗传算法和模拟退火算法的优点,在信号的压缩感知应用研究方面取得了较好的进展。



2 基于GASA的CS信号重构方法
2.1 确定稀疏表示的各非零元素位置信息


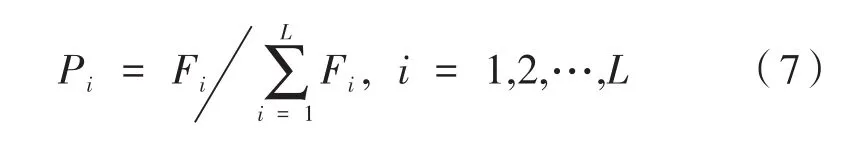



2.2 确定稀疏表示的各非零元素幅度信息

2.3 GASA的CS重构方法
3 实验结果及分析
3.1 GASA的CS重构方法对一维稀疏信号重构

3.2 GASA的CS重构方法对图像的重构

3.3 GASA的CS重构方法对图像重构的精度

4 结论

