X射线超反射镜鲁棒性膜系设计

陶保全，郭祥帅，李博涵，匡尚奇，李超逸

（长春理工大学 理学院，长春 130022）

近年来，X射线超反射镜已成功应用于X射线天文学、光谱学和同步辐射等相关研究领域。X射线超反射镜是一种非周期的多层膜，其膜系的各个膜层具有不同几何厚度，可以使不同入射角度或入射能量的X射线在膜系各层获得不同的反射，通过相干叠加获得反射平台。与传统等周期多层膜构成的光学元件相比，X射线超反射镜具有更宽、更平坦的反射平台，能增加掠入射光学系统的掠入射角或扩展其能量工作范围，可用于星载X射线望远镜、同步辐射装置和X射线显微成像等等，并可显著地提升这些装备的性能［1-2］。2000年以来，X射线超反射镜的设计方法主要有三种：经验公式的解析方法［3］、解析加数值优化的方法［4-6］和全数值计算方法。前两种方法设计的膜系，反射平台通常有比较大的振荡，但受当时计算机性能和算法的限制，最后一种方法应用较少。近几年，随着计算机技术的发展，完全基于优化算法的设计方法开始被广泛使用［7-10］，计算所需的时间与计算量变得越来越能够接受，各种优化算法的出现极大地提升了超反射镜设计的光学性能。

虽然X射线多层膜系统的设计在光学性能方面取得了成功，但在实际制作中仍存在问题。相比用于可见光波段的多层膜，X射线超反射镜的膜层厚度薄约100倍，膜层数多约10倍［11］，即各膜层的厚度都非常薄，通常只有几纳米，并且膜系结构往往比较复杂，这使得超反射镜的膜层厚度控制在实际制备中并非易事，极小的镀膜误差都会造成反射性能严重退化，因此极高的膜厚控制要求使得只有少数高水平机构能够制造。此时，光学性能不再是多层膜设计的唯一追求，还应该引入薄膜实际可镀性的主动优化设计思想，将膜系对膜厚误差的灵敏度加以优化和控制。

对此，多目标优化算法有希望获得掠入射X射线反射性能优秀并且对膜厚误差敏感度更低的鲁棒性超反射镜设计。此前的鲁棒性设计研究在正入射极紫外多层膜系统中进行了一些尝试［12-14］。然而，对于波长更短的X射线，掠入射X射线多层膜的鲁棒性设计与之前的设计不同。在以往的多层膜设计中，默认入射光为不发散的平行入射光。而在掠入射反射的X射线多层膜反射镜设计中，入射光的发散角对超反射镜反射率的影响不可忽视，需要在反射率计算过程中加以考虑。X射线超反射镜鲁棒性膜系的设计方法基于非支配排序遗传算法（NSGA-Ⅱ），这是一种基于Pareto最优解的多目标优化算法［15-16］。以X射线多层膜常用的W和C作为膜层设计的材料对设计鲁棒性X射线超反射镜，并与基于传统方法的膜系设计进行对比，研究结果证明鲁棒性设计方法在提升超反射镜的可制备性、降低其光谱性能退化方面具有独特优势。

1 设计方法

特征矩阵法是计算多层膜系统反射率的一种常用方法，同时由于反射率对界面粗糙度非常敏感，在模拟中考虑了界面粗糙度对反射率的影响。计算光学常数的原子散射因子数据从文献［17］中获得，多层膜系统反射率计算的具体细节可参见文献［12，18，19］，多层膜表面反射率用R表示。在实际情况中，掠入射到超反射镜的X射线具有一个发散角，实际测得的反射率为反射率和光强分布函数的卷积［20］。因此，在模拟中将算得的反射率修改为R'（θ0），其表示为：

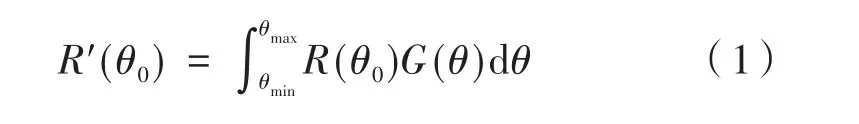
其中，θ0为掠入射角；θmin和 θmax为发散角 θ的边界。描述X射线掠入射光强分布的函数G（θ）呈正态分布，可表示为：

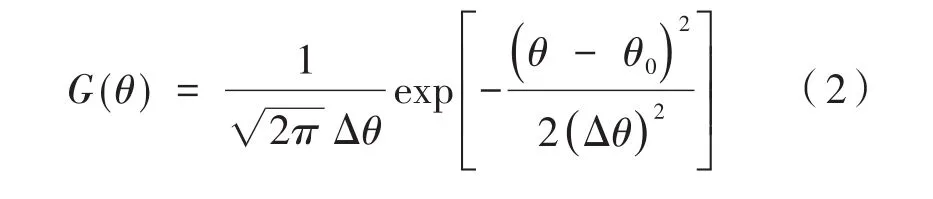
其中，∆θ=0.18 mrad。在这里，给出多层膜设计的两个评价函数。首先给出多层膜反射率的评价函数：

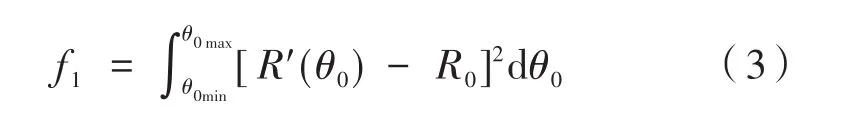
其中，R'和R0分别为所设计多层膜的计算反射率和目标反射率。评价函数f1为计算得到的反射率与需求的反射率差的平方和，根据多层膜膜系厚度误差对光学性能影响的推导［21-22］，给出鲁棒性评价函数：

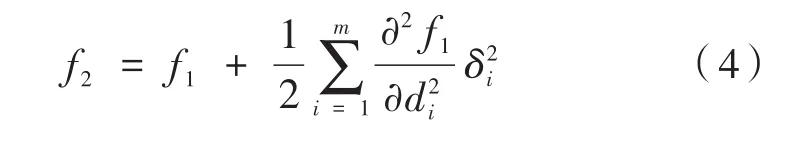
其中，di和δi分别为第i层膜的厚度和膜厚误差的标准差；i是从基底向入射介质计数的膜层编号；m是多层膜的膜层总数。f2评价了膜系反射性能对膜厚误差的灵敏度。将f1和f2作为NS‐GA-Ⅱ算法两个优化目标的评价函数进行优化。

在X射线波段，所有材料都具有较强的吸收，所以过多的膜层对并不能明显提高X射线超反射镜的反射率，并且由于镀膜工艺限制，不能无限地增加膜层数。因此将W/C材料对的数量设为 30对，膜系结构为 Sub/［W/C］30，其中 Sub代表基底。设超反射镜基底、最外层、中间层的界面粗糙度均方根值分别为0.1 nm、0.5 nm和0.3 nm。为避免不同膜层之间界面属性因膜层几何厚度变化过大而发生改变，算法搜索多层膜中各个膜层的厚度范围被设定在2～6 nm内。NSGA-Ⅱ算法的参数设置如下：种群规模为100；进化代数为10 000；交叉概率Pc=1.0；变异概率Pm=1/30；交叉和变异的分布指数分别为ηc=1、ηm=1。

2 结果与讨论

为了验证鲁棒性超反射镜设计方法的效果，分别设计了具有掠入射角度和能量带宽的X射线超反射镜。

2.1 宽角度超反射镜设计

在掠入射角度带宽的超反射镜设计中，设入射光线为Cu Kα射线（8 keV），掠入射角的角度带宽为［0.9°，1.1°］，目标反射率R0=20%。图1展示的是不同进化代数时NSGA-II算法获得的非支配解，横纵坐标分别为反射率评价函数f1和鲁棒性评价函数f2。作为与鲁棒性设计进行对比的传统设计代表，使用遗传算法（GA）只优化评价函数f1得到了膜系设计，命名为GA设计。为了便于比较，将单目标优化的GA设计在鲁棒性设计双目标评价函数空间上的位置也进行了标注。鲁棒性设计的非支配前沿在收敛之前会有一些解分布较为孤立，但最终得到非支配解的分布较为均匀。非支配解集具有多样性，一次优化设计能提供较多可选的设计方案，设计人员可以根据需要在其中选择。随着优化次数的增加，非支配解逐渐向具有更小评价函数值的方向收敛，说明膜系设计的反射性能和鲁棒性能被同时优化。在非支配前沿中可以看出，两个优化目标之间存在互相限制的关系，即非支配解某一个性能较优秀的同时另一性能就会表现较差，这与此前报道的极紫外多层膜的研究结果是一致的［12-13］。单就评价函数的值来看，GA设计反射性能更优秀，但鲁棒性很差。在鲁棒性设计的非支配前沿中，为保证膜系反射性能，选择其中具有最小评价函数f1值的边界解作为鲁棒性设计的代表与GA设计进行对比，并将其命名为NSGA-Ⅱ设计。GA设计和NSGA-Ⅱ设计在图1中用实心三角形标注。

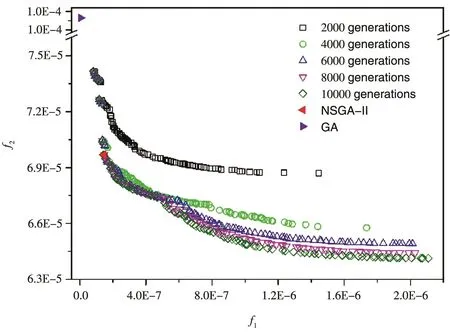
图1 在宽角度超反射镜设计中，NSGA-Ⅱ算法不同进化代数所获得的非支配解

图2展示了NSGA-Ⅱ设计和GA设计的膜系结构。可以看到，两种设计的膜厚分布有着明显差别，表明反射平台平稳的膜系设计不是唯一的，由于优化目标不完全相同，最后得到的膜系结构也明显不同，鲁棒性设计方法将得到对误差敏感度更低的膜系。

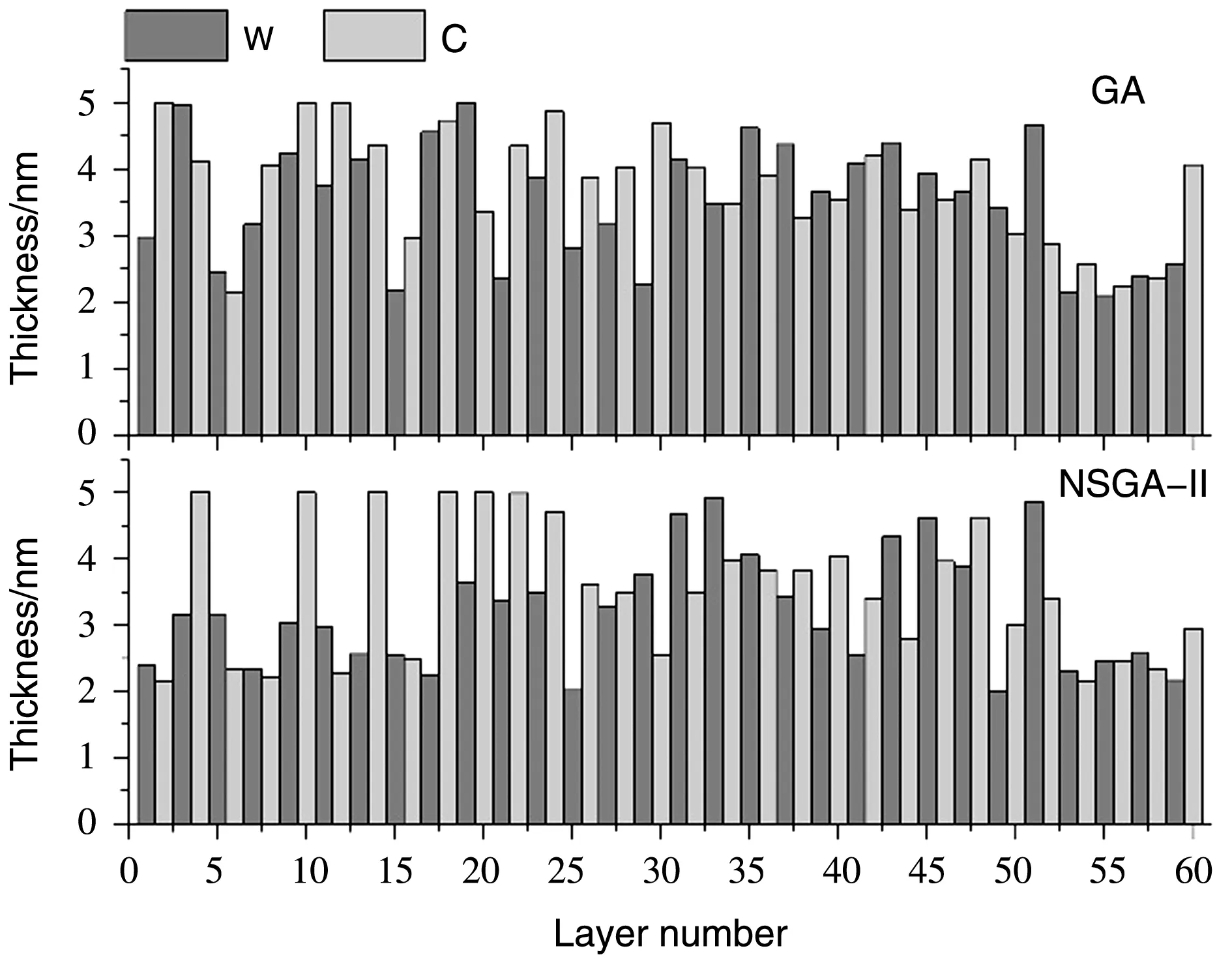
图2 宽角度带宽超反射镜设计中，传统（GA）设计与鲁棒（NSGA-Ⅱ）设计的膜系结构

造成膜厚误差的原因有很多，如监测方法的误差、腔体清洁度、基底温度等，所以膜厚误差是随机的，其分布可以用正态分布来描述。在设计中，设多层膜系统中的每一层的厚度误差互不相关，数学期望为零，误差的标准差δi=0.1 nm。为了分析引入膜厚误差后超反射镜设计的反射平台偏差，用下面的公式计算期望反射及其标准差通道：

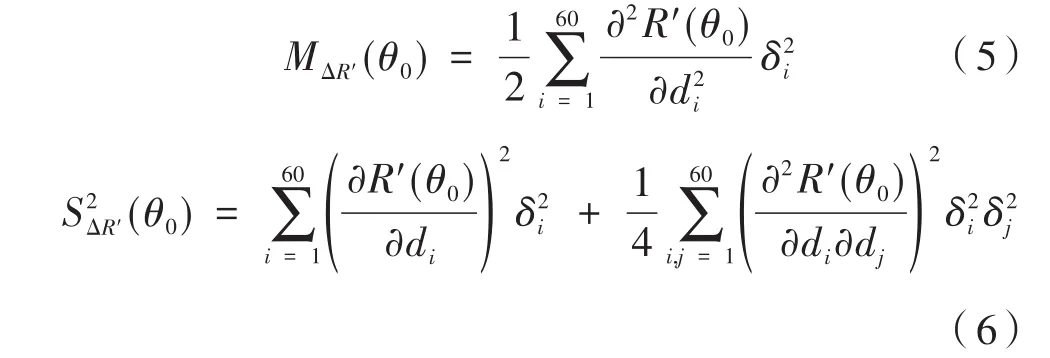
其中，di，dj和δi，δj分别为第i和第j层膜的几何厚度和厚度误差的标准差；R'+M△R'为反射光谱的数学期望；R'+M△R'±S△R'为反射光谱的标准差通道。

图3为X射线宽角度超反射镜的NSGA-Ⅱ设计和GA设计在未引入膜厚误差的理想情况下膜系结构反演得到的反射率光谱。由于多层膜系统的膜厚分布不同导致在目标带宽范围外反射率存在不同，但在目标角度带宽内两种设计的反射率稳定保持在20%，反射光谱平台平滑，波动性很小。虽然NSGA-Ⅱ设计评价函数f1的值略逊于GA设计，但它的反射性能可以满足需求。需要注意的是，这只是未引入膜厚误差的理想状态下的反射率光谱，实际制造将不可避免的产生误差，因此更该关注超反射镜实际可能出现的反射光谱。引入膜厚随机误差后GA设计和NSGA-Ⅱ设计的期望反射光谱R'+M△R'及其标准差通道R'+M△R'+S△R'如图4所示。标准差通道R'+M△R'+S△R'两条曲线之间区域是超反射镜在引入膜厚随机误差后反射平台的分布范围。标准差通道越窄，说明膜厚误差导致的反射光谱波动越小。可以看出，在大部分角度带宽内，NSGA-II设计的反射平台对膜厚误差的敏感度比GA设计更低，NSGA-II设计膜系的光学性能受膜厚随机误差影响较小，镀膜风险较低。

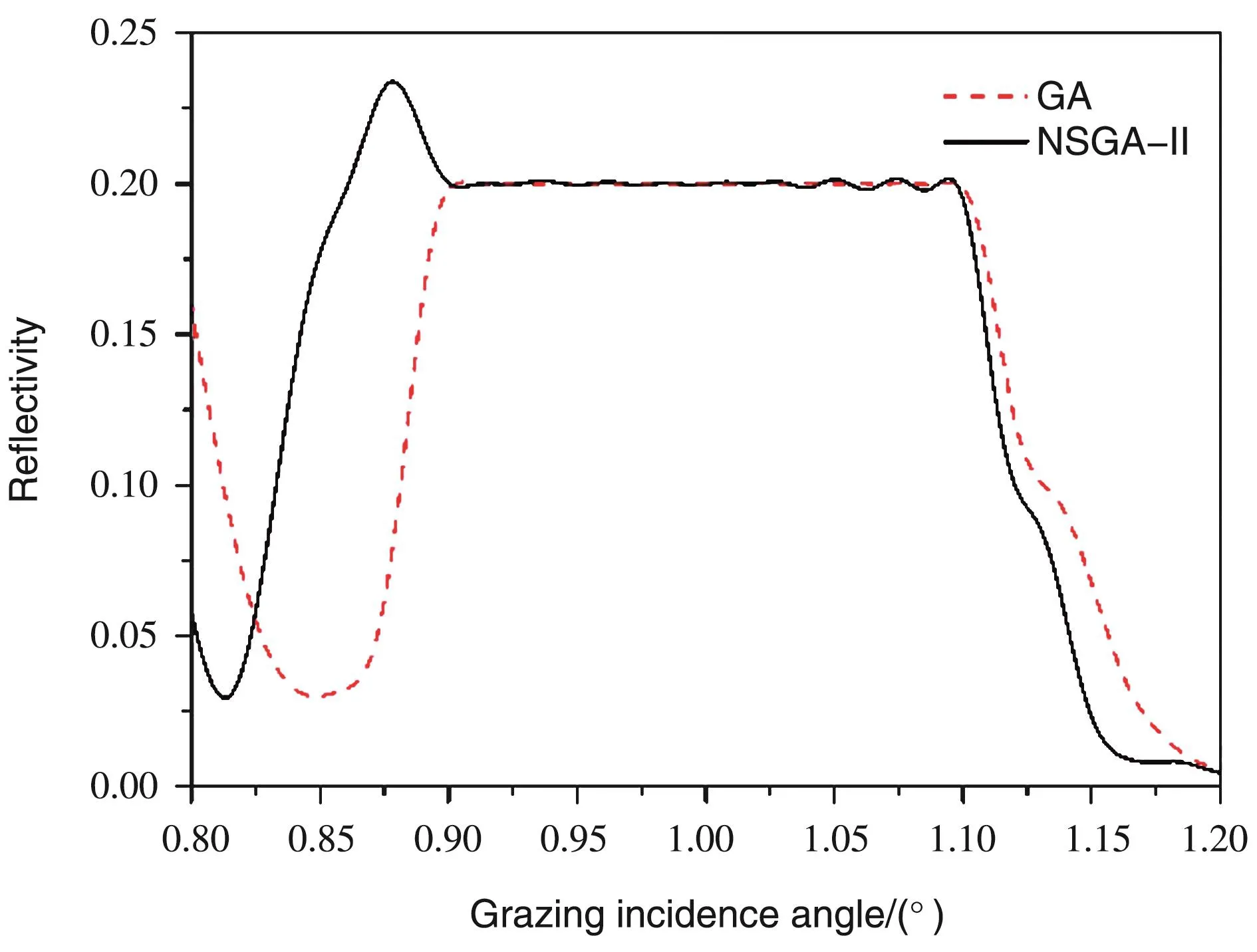
图3 在宽角度超反射镜设计中，GA设计与NSGA-Ⅱ设计的理论反射光谱

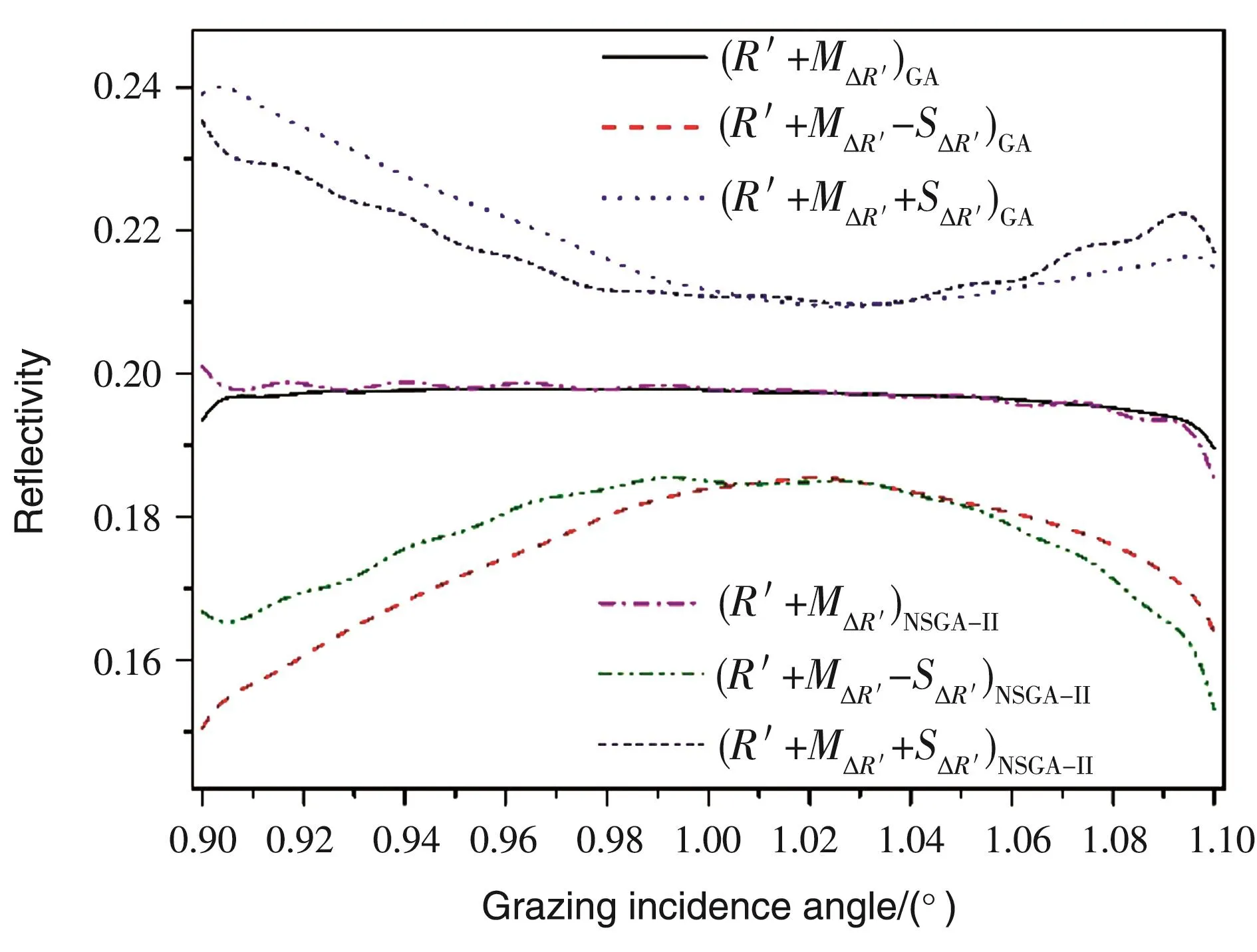
图4 在宽角度超反射镜设计中，GA设计与NSGA-Ⅱ设计的期望反射光谱及其标准差通道

2.2 宽能带超反射镜设计

如果式（3）中代表入射角度的“θ0”替换成代表射线能量的”λ”。评价函数f1和f2可设计具有宽能量带宽的X射线超反射镜鲁棒性膜系，式（3）修改为：

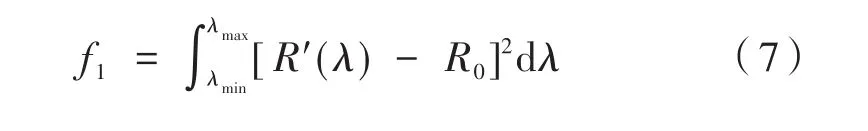
设超反射镜的能量带宽为18.5～21.5 keV，掠入射角为0.5°，目标反射率R0=20%。NSGA-II算法获得的非支配解如图5所示，宽能量带宽超反射镜设计的结果收敛较宽角度超反射镜更慢。宽角度超反射镜设计中涉及的光学常数较少，非支配前沿在大约6 000代时开始收敛，收敛较快；而宽能带超反射镜设计涉及使用较多的光学常数，使得非支配前沿收敛较晚，在大约8 000代开始收敛，并且宽能带超反射镜设计的非支配前沿分布比宽角度设计更均匀。宽能带带宽超反射镜设计中，NSGA-Ⅱ设计的选取策略与宽角度设计相同。图6展示了NSGA-Ⅱ设计和GA设计的膜系结构，可以看出，NSGA-Ⅱ设计与GA设计的各膜层厚度明显不同。即使是在目标带宽之外，这两种设计的反射率曲线都很相似，NSGA-Ⅱ设计和GA设计未引入膜厚误差时膜系结构反演得到的反射率光谱如图7所示。这进一步印证了鲁棒性设计方法得到低膜厚误差敏感度膜系设计的可行性。

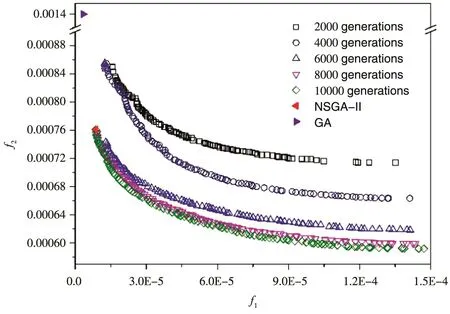
图5 在宽能带X射线超反射镜设计中，NSGA-Ⅱ算法不同进化代数所获得的非支配解

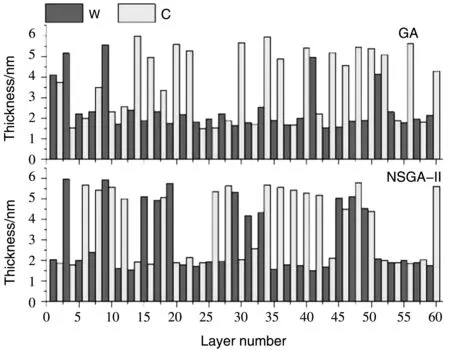
图6 宽能带超反射镜设计中，传统（GA）设计与鲁棒（NSGA-Ⅱ）设计的膜系结构

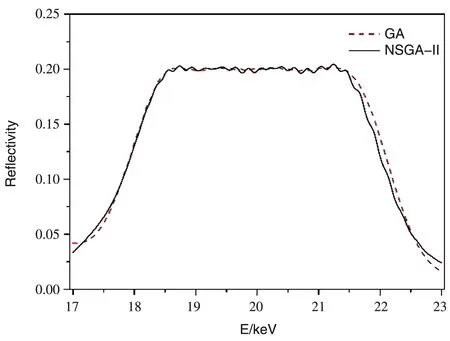
图7 宽能带X射线超反射镜设计中GA设计与NSGA-Ⅱ设计的理论反射光谱

将式（5）和式（6）中的符号“θ0”替换为“λ”，可以得到宽能量带宽X射线超反射镜设计期望反射光谱及其标准差通道，如图8所示。在引入膜厚随机误差后，NSGA-II设计的反射率标准差通道几乎全部包含在GA设计的偏差范围中，也就是说，鲁棒性设计方法能将膜厚误差造成的反射带偏差控制在一个更小的范围之内。对比分析表明，宽能带X射线超反射镜的鲁棒性设计效果优于宽角度设计，这是由于宽能带X射线超反射镜设计两个优化目标之间的约束关系较弱造成的。鲁棒性膜系设计的膜厚误差敏感度控制效果比较理想，这将提升超反射镜的实际可制备性能。证明基于NSGA-II的超反射镜鲁棒性设计方法是一种可行的方法，具有很好的应用前景。

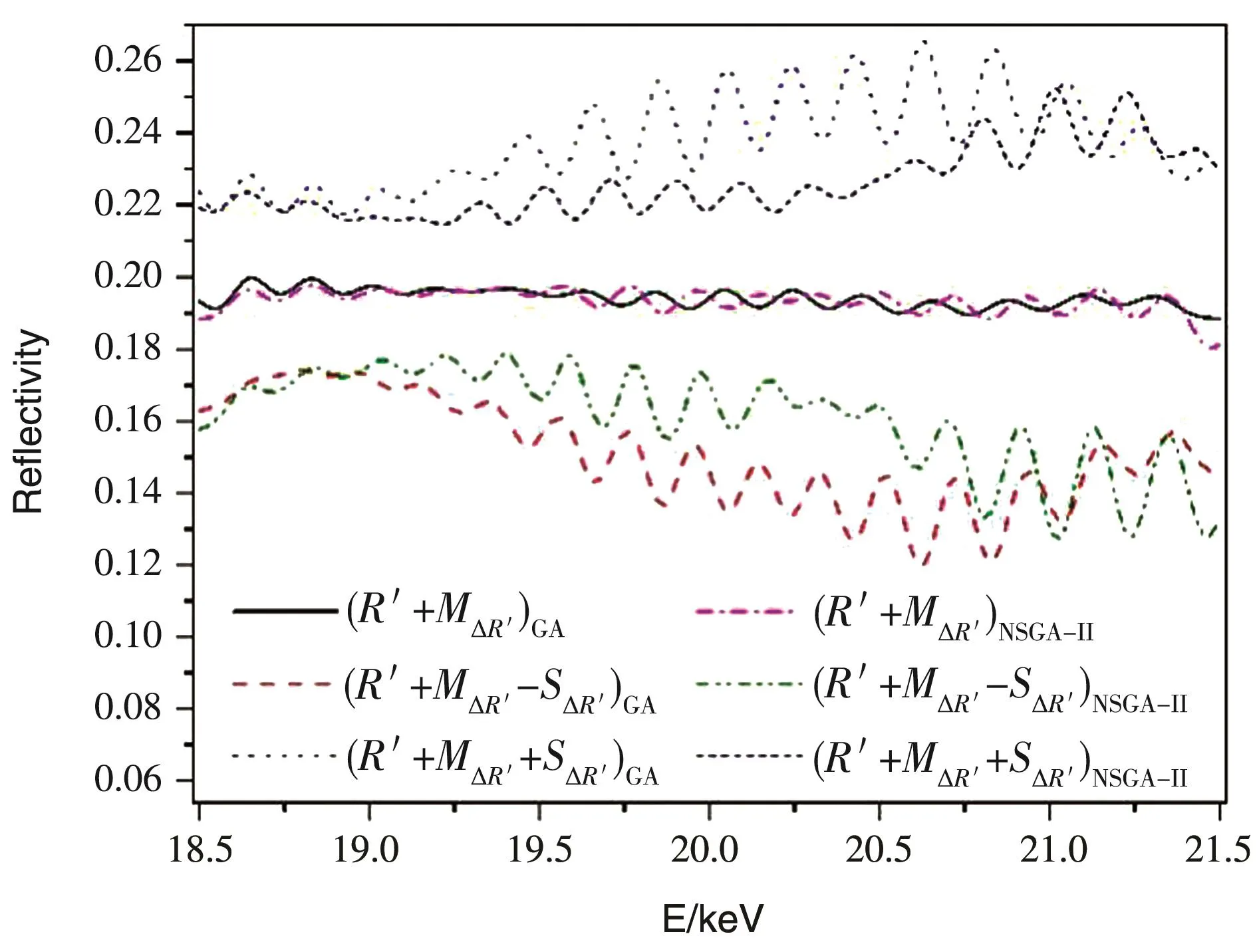
图8 宽能带X射线超反射镜设计中GA设计与NSGA-Ⅱ设计的期望反射光谱及其标准差通道

3 结论

角度带宽和能量带宽的超反射镜设计结果表明，相比传统的单目标优化设计方法，基于NSGA-Ⅱ算法的鲁棒性X射线超反射镜设计方法在满足反射性能要求的同时显著降低了超反射镜对膜厚随机误差的敏感程度，这将有助于减小超反射镜制造过程随机膜厚误差造成的反射带偏差。在设计中考虑发散角对超反镜反射率的影响，对于掠入射X射线多层膜反射镜的设计来说非常重要，这更符合硬X射线光学系统的设计要求。基于多目标优化算法的鲁棒性多层膜膜系设计方法由于其在光学性能和制造上的综合优势，展现出很大的应用价值，在推广高质量X射线多层膜制备方面有较大潜力。