矩阵特征值与特征向量的几何意义
雍龙泉
(陕西理工大学 数学与计算机科学学院, 陕西 汉中 723000)
特征值与特征向量是《高等代数》《线性代数》《矩阵论》中的两个重要概念,目前被广泛应用于动力系统、机器学习、图像处理、数据挖掘等热点领域中[1-3]。现行教材在给出其定义之前缺少引入过程,使得特征值与特征向量的概念抽象难懂,更显得突兀,导致学生接受困难[4-11]。本文以2阶方阵为例,重点阐述特征值与特征向量的几何意义。
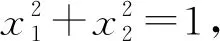
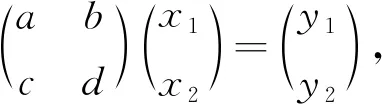
(1)
下面从几何上来研究向量y=(y1,y2)T随着x=(x1,x2)T变化的轨迹分布。
1 矩阵A可逆时
矩阵A可逆,即ad-bc≠0。当ac+bd=0时,则方程(1)表示一个椭圆,且椭圆的长轴与短轴分别在坐标轴上;当ac+bd≠0时,则方程(1)还是一个椭圆,此时椭圆的长轴与短轴不在坐标轴上。下面举例说明。
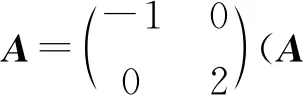
(2)
方程(2)表示一个椭圆,其长轴与短轴在坐标轴上,如图1所示。例1表明,通过该线性变换,单位圆变成了一个椭圆。

图1 线性变换的轨迹
当x位于水平方向,如图2(a)所示;当x位于竖直方向,如图2(b)所示。
此时两个向量共线,即

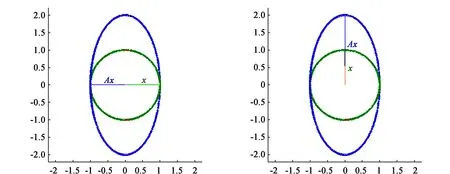
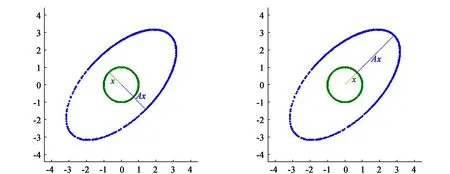
(a)特征值-1对应的特征向量 (b)特征值2对应的特征向量图2 特征值与特征向量的几何意义

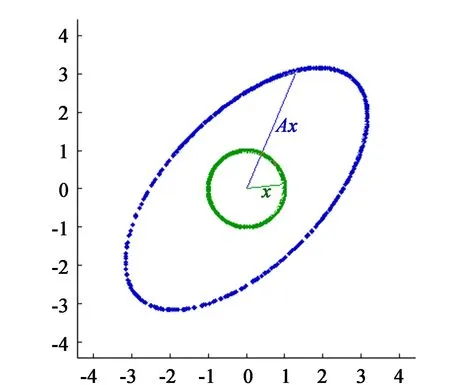
图3 线性变换的轨迹
(3)
方程(3)表示一个椭圆,其长轴与短轴不在坐标轴上,如图3所示。
例2表明,通过该线性变换,单位圆变成了一个长轴与短轴均不在坐标轴上的椭圆。
由于
(a)特征值-2对应的特征向量 (b)特征值4对应的特征向量图4 特征值与特征向量的几何意义

图5 线性变换的轨迹

(4)
方程(4)表示一个长轴与短轴不在坐标轴上的椭圆,如图5所示。
由于
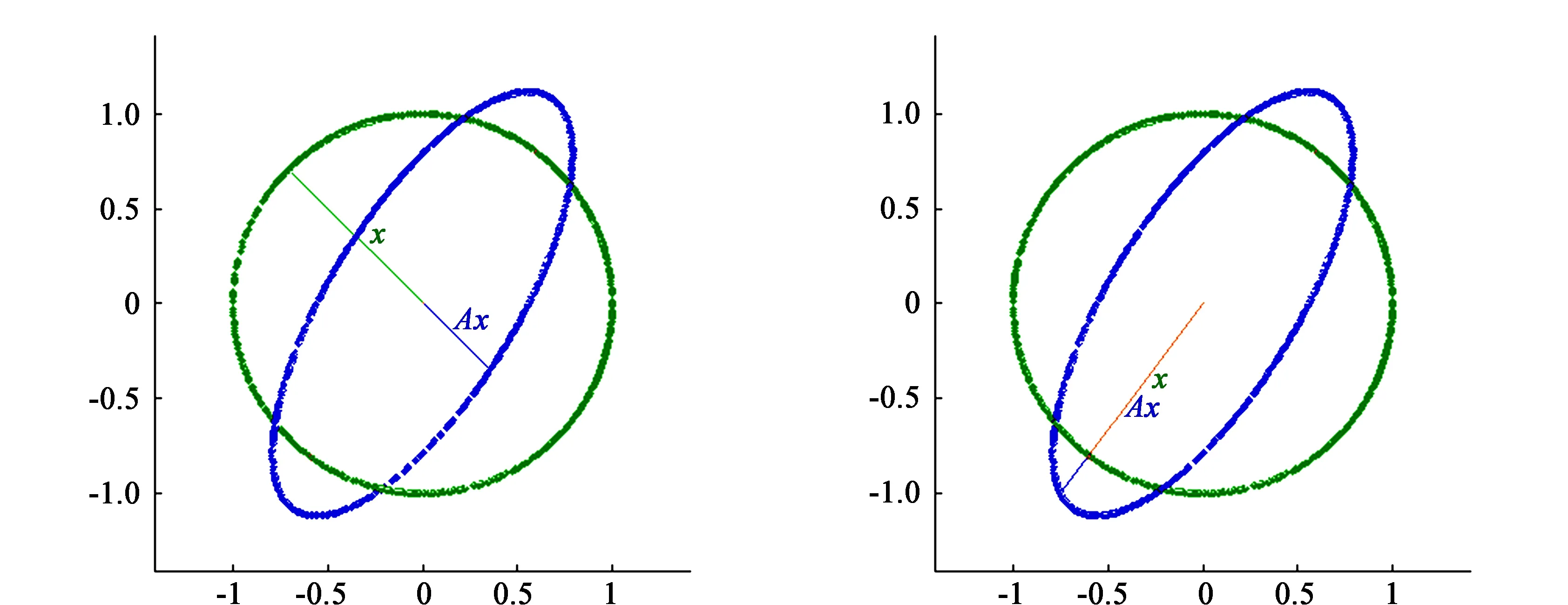
(a)特征值-1/2对应的特征向量 (b)特征值5/4对应的特征向量图6 特征值与特征向量的几何意义

图7 线性变换的轨迹

(5)
这表明,通过该线性变换,单位圆变成了一个椭圆,此时椭圆的长轴与短轴不在坐标轴上,如图7所示。
由于该矩阵在实数域上没有特征值和特征向量,因此Ax与x始终不能重合。
事实上,该矩阵的特征值为
注:本文重点研究特征值为实数时矩阵特征值与特征向量的几何意义;特征值与特征向量为复数时几何意义不明显。
2 矩阵A不可逆时
矩阵A不可逆,即ad-bc=0,这时方程(1)变化为
(6)
下面举例说明方程(6)表示的曲线。
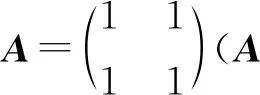
(7)
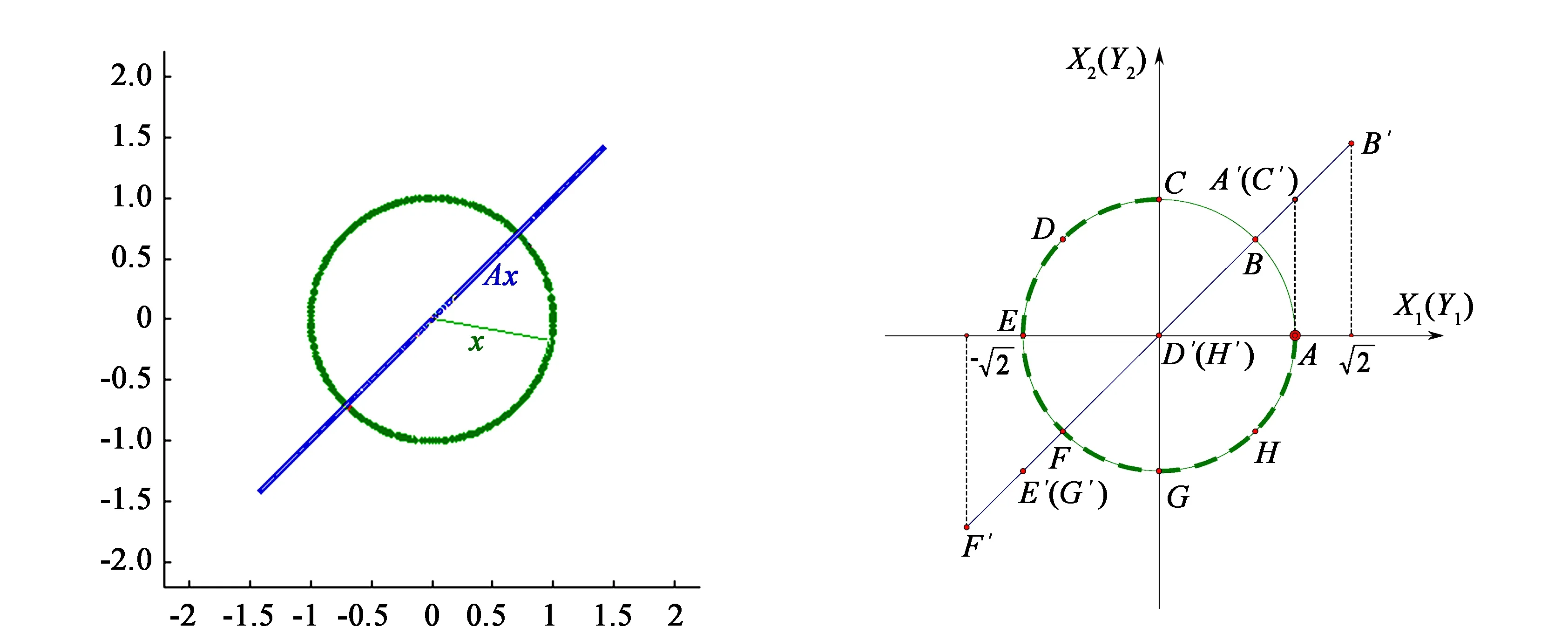
(a)单位圆变换为线段 (b)点的对应关系图8 线性变换的轨迹
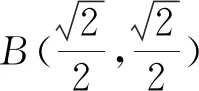
由于
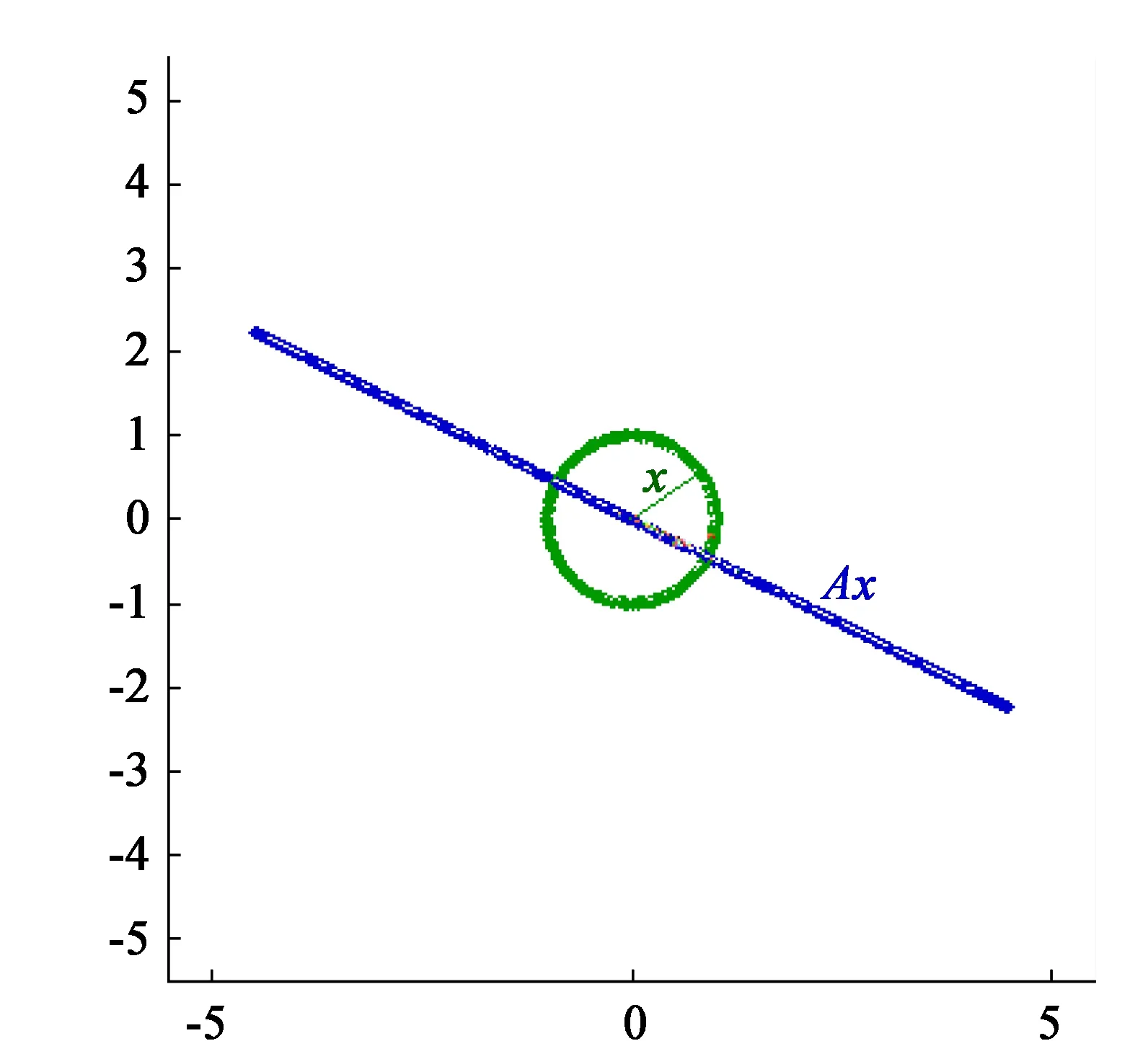
图9 线性变换的轨迹

(8)
由于该矩阵对应的特征值为0,且0为2重特征根。对应的单位化特征向量
3 结语
本文首次以矩阵的可逆性、对称性作为分类原则,通过线性变换的不变量引入特征向量与特征值的概念,能够帮助学生更好地理解矩阵特征值与特征向量的定义。

