预应力连接预制拼装综合管廊地震响应分析

陈学雄

(福建省交通建设质量安全中心， 福建 福州 350001)

地下综合管廊又称共同沟，是将燃气、电力、电信、给排水等两种或两种以上的生命线工程设施共同敷设与其中的地下结构[1]。近年来，综合管廊以其独有的集约化、规范化优势在许多发达国家已经得到广泛的应用[2]。相较于发达国家，我国在综合管廊方面研究起步较晚，但近年来在广州、宁波、厦门及平潭等多个城市和地区都兴修起了地下管廊[3]。与此同时我国学者也开展了许多相关的研究，尤其在综合管廊抗震方面，诸多学者基于综合管廊抗震已经做了些许研究。史晓军等[1]开展了地下综合管廊振动台研究，指出综合管廊结构地震响应服从周围土体响应，且顶、底、侧板土压力分布模式不同，在地震作用下均发生位移，同时伴随刚体的转动。蒋录珍等[4-6]开展了非一致激励下综合管廊振动台模型试验研究，指出地震动的非一致性和接触面破坏共同导致了结构接头的响应，且只有在纵向非一致激励下，结构才会有纵向内力响应。冯瑞成[7]进行了共同沟振动台试验，得出共同沟在强震下依然会发生破坏，内部管线受地震加速度峰值影响较大，并指出共同沟存在土-结作用力，最大动土压力出现在结构底板。顾卫兵等[8]通过静力加载方式研究了预制预应力管廊和普通管廊受力性能，指出装配式管廊破坏荷载比普通管廊减少14%，加腋区的存在减少顶板的竖向挠度。吕荔炫[9]研究了不同埋深情况下地下综合管廊的受力性能，指出随着埋深的增加，管廊的混凝土应力、位移、钢筋应力逐渐增大，且呈线性关系。

尽管众多学者已经对地下综合管廊的抗震性能和力学性能开展了许多相关研究，但目前针对综合管廊抗震研究，首先大多数是基于现浇综合管廊的抗震性能进行研究，对于预制节段装配式综合管廊的研究较为匮乏，而两者的区别是客观存在的；其次综合管廊系长线型地下结构，纵向受尺寸效应影响较大，缩尺模型试验中其性能将大为改变，非线性破坏模式的存在也使其动力相似成为一个难题；第三，目前的简化设计分析大多基于平面应变分析，该简化分析方法的适用性尚需科学论证，然而地下结构因其复杂的非线性特性，在横向地震力作用下变形特征与破坏形态皆为三维，故与横截面法向平行的纵向段变形及内力不容忽视。在此基础上，本文基于弹塑性时程分析建立精确完善的三维有限元模型，对预制节段拼装综合管廊进行抗震性能研究分析，以期对预制节段拼装综合管廊结构的抗震分析提供依据。

1 有限元模型

1.1 工程背景

本文讨论的综合管廊工程位于福建省平潭岛东部沿海，总体呈南北走向，环岛东路两侧，道路设计全长22.577 km，红线宽度60～75 m，属城市快速路。综合管廊截面采用单仓结构形式，除过河段管廊受道路纵坡和设计水位限制，标准段管廊断面大小为3.9 m×4.1 m，顶底板及腹板壁厚35 cm；管廊终点段局部采用渐变，与安海路管廊顺接。场地地层结构及岩性特征自上而下分布有填中砂或素填土、淤泥、粉质黏土、淤泥质土、卵石、粉质黏土、中砂、残积黏性土、全风化花岗岩、砂土状强风化花岗岩、碎块状强风化花岗岩等。各土层的分布、厚度和性能变化较大。场地地基土在水平及垂直方向上均匀性较差，属不均匀地基，地基稳定性总体较差。总体上本工程沿线场地浅部均为填中砂，中砂层为良好的路基填料，填砂下部存在深厚软弱层淤泥，工后沉降变形较大。土层物理参数见表1。

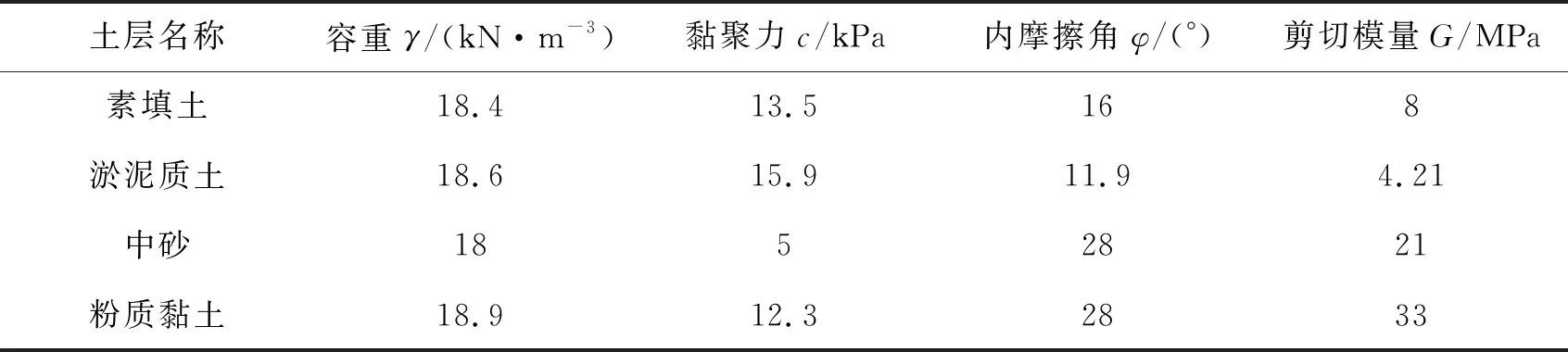
表1 土层物理参数

1.2 基本假设

有限元的建模及求解实质上是对现实连续问题的离散分析，本质上是对复杂问题的一种简化。因此，在对现实工程进行建模求解时，应把握住关键问题，对其进行精细化建模求解；而对于次要问题则应该简要分析，有效利用好现有资源，以最大化的提高计算效率。因此本文建模时做了如下的基本假设：

(1)假设场地各层土体为均质土体，不考虑各向异性；

(2)假设地下结构地震激励来自于假想基岩面，且为一致性激励，暂不考虑行波效应；

(3)不考虑地震作用导致的土体孔隙水压力的变化及土体地基失稳等问题；

(4)假定该管廊工程为独立结构，周边无其他结构相互影响。

1.3 有限元模型建立

1.3.1 模型信息

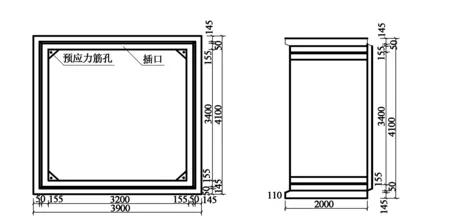
(a)横截面 (b)侧截面图1 管廊横截面与侧截面图

本文选取环湖路预制标准段进行分析，根据地勘资料，该段处于粉质黏土及中砂土层，管廊标准段结构如图1所示。

利用ABAQUS对管廊主体结构进行三维实体建模分析[10]，主体结构采用C40混凝土，在ABAQUS中采用混凝土损伤塑形进行模拟，对于土体、结构均采用实体模型C3D8R进行模拟，土体模型尺寸为28 m×12 m×20 m，管廊的覆土厚度为2 m；钢筋采用HRB400级钢筋，预应力筋采用预应力钢绞线1-7φ15.2，钢筋材料使用双折线模型，钢筋及预应力钢绞线均采用TRUSS单元进行模拟，两端采用MPC约束进行端点耦合，并通过初始应力法来施加预应力，其中预应力根据工程实际取150 kN。整体有限元模型及管廊精细模型如图2所示，其中结点个数为5376，单元个数为4100。

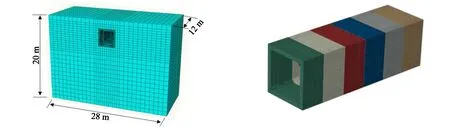
(a)整体有限元模型 (b)六节管廊图图2 管廊有限元模型

1.3.2 地震波选取及监控点布置

参照地勘资料可知，拟建场地抗震设防烈度为7度，基本地震加速度值为0.10g，设计分组为第三组，场地类别属Ⅱ类区段，地震特征周期为0.45 s。根据《建筑工程抗震性态设计通则》，主要采用Kobe波对预制节段拼装综合管廊进行抗震分析，输入方向为X向(即横向)，持时为13 s，并对该地震波进行相应的加速度幅值调整，采用典型地震波处理软件SeismoSignal进行滤波与基线修正，修正后地震波如图3所示。

为观察及探究预制节段拼装综合管廊在地震作用下的响应特点，选取第三节管节作为监控对象，监测点1位于管节左上角，监测点2位于腋角处，底板监测点位于管节底板中点，具体布置见图4。

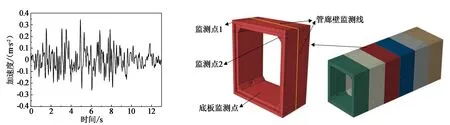
图3 Kobe波加速度时程曲线 图4 监测管节及监控点说明图

1.3.3 模型本构

在地下结构的抗震分析中可采用非线性和等效线性两种方式，从理论上讲非线性更符合实际情况，但是所需的计算参数较为复杂，且计算耗费时间较长，一般仅适用于一维场地分析，在三维地震分析中，等效线性方法可以通过不断迭代逼近来反应土体非弹性与非线性以取得预期效果，该方式计算高效，且在地震加速度小于0.4g的情况下能提供较为合理的结果，固采用等效线性动黏弹性模型来模拟土体本构[11]。

等效线性模型在进行动力计算时，应先假定材料剪切模量值及阻尼比值，而后根据求得的土层平均应变来确定对应的剪切模量和阻尼比，通过反复迭代计算逼近预期结果。

在ABAQUS中没有自带等效线性本构，需要通过UMAT用户子程序进行编写导入。UMAT用户子程序系采用FORTRAN语言编写，用户需提供材料积分点雅克比矩阵以完成本构关系的开发。在本文中采用UMAT用户子程序的过程如下：

(1)通过*initial conditions，type=solution导入各单元有效应力，作为状态变量STATEV(1)，在后续分析中供UMAT子程序调用；

(2)在UMAT子程序中将单元最大剪应变存储为STATEV(2)；

(3)通过编写的FORTRAN语言将根据应变水平确定的等效剪切模量和等效阻尼比存储为状态变量STATEV(3)和STATEV(4)；

(4)最后将4个状态变量作为初始变量替换第一步中*initial conditions， type=solution导入的变量来完成迭代计算。

采用等效土体来代替计算，等效土体参数见表2。

表2 等效土体参数

管廊主体结构采用C40混凝土，在ABAQUS中采用混凝土损伤塑形进行模拟，钢筋采用HRB400级钢筋，预应力筋采用预应力钢绞线1-7φ15.2，其中钢筋材料使用双折线模型。

1.3.4 动力边界条件

目前常用的局部人工边界有黏性边界、透射边界、黏弹性边界[12]。黏弹性人工边界是基于黏性边界的基础上，通过施加弹性元件来模拟远域地基的弹性变形，有效地解决了黏性边界低频失稳的问题，同时在边界设定上无需像透射边界一样设置大量内点单元，求解效率高且精确度较好，具有较高的适应性。

本文采用的集中黏弹性人工边界的具体实现方法是在边界处离散分布弹簧和阻尼器，分别用来模拟边界远域处弹性恢复性能和抵消散射波在边界处的反射效应，在ABAQUS隐式算法中采用Springs和Dashpots来实现弹簧和阻尼器的添加，即在边界节点处使用Springs和Dashpots代替传统静力边界，完成动力边界的建立。

1.3.5 土体-结构动力接触

在基于SUSI效应下的地下结构动力计算中，接触作用扮演着至关重要的角色，由于土体与结构变形的非协调性，在动力分析中接触面的传力方式也会影响到后续的响应。在有限元计算中，模拟接触的方法通常有两种：接触单元法和接触面对法。接触单元法系在两预定义接触主体之间建立一接触单元，通过给予接触单元本构关系来等效接触行为，但在发生大变形以及接触面分开时，该方法容易产生矩阵奇异问题，故该方法于静力分析中会取得较好的成效。接触面对法在预定义接触主体上分别设定接触面，以形成接触对，并预设接触对的力学传递性质，结合接触面对来建立接触方程，通过接触算法求解接触方程。相较于接触单元法的局限性，接触面对法能有效地模拟接触面大变形、大滑移以及接触面张开闭合连续转换的复杂动力接触问题。本文所采用的商业有限元软件ABAQUS正是采用接触面对法来模拟实现接触行为。

2 地震动响应分析

2.1 地震动强度

根据《GBT51336—2018地下结构抗震设计标准》，将Kobe波分别调整为0.1g、0.2g、0.3g来考察地震动强度对管廊结构的地震响应影响。主要从加速度响应、位移响应、应力响应及接头响应4个方面进行分析。

2.1.1 加速度响应

3个不同强度Kobe波作用下土体底部加速度时程曲线及监测管节底部加速度时程曲线如图5所示，可见：

(1)随着地震动强度的增大，管廊结构的地震响应随之增大。0.1gKobe波作用时，管廊底部加速度峰值为1.07 m/s2，0.2g时为1.98 m/s2，0.3g时为3.69 m/s2，即Kobe波每增大0.1g，管廊结构的加速度峰值增大1.85倍。

(2)地震波在由基岩传播至地下结构过程中，其频谱基本保持不变，不会在传播过程中发生畸变，其强度的大小变化不会对其产生影响。

(3)基岩加速度时程峰值略大于输入地震波加速度时程峰值，0.1gKobe波作用下基岩加速度峰值为1.29 m/s2，输入地震波加速度峰值为1.07 m/s2,约为输入时的1.2倍。造成该情况系由于地震波在向上传播的过程中会发生反射并与先前地震波叠加形成放大效应，这也符合一维波动理论下的地震动传播情形[13]。

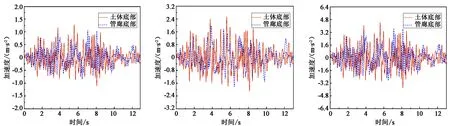
(a)0.1g (b)0.2g (c)0.3g图5 不同强度Kobe波地震作用下管廊底部及土体底部加速度时程曲线

2.1.2 位移响应

在不同强度的Kobe波作用下某时刻管廊结构的侧壁相对水平位移如图6所示。由计算结果可以看出：

(1)随着地震动强度的增大，管廊结构的位移响应随之增大，管廊侧壁高度均为4 m时，0.1gKobe波相对水平位移值为1.311 6 mm，0.2gKobe波作用时为2.623 2 mm，0.3gKobe波作用时为4.525 9 mm，即同一侧壁高度下Kobe波每增加0.1g，相对水平位移约增加一倍。

(2)由于左右两侧壁都存在着相对水平位移，故管廊整体结构在地震作用下会呈现轻微的偏转现象，即结构随着地震波而震荡，该现象随着地震动强度的增大而增大，在大强度地震作用下会对结构产生一定的磨损。

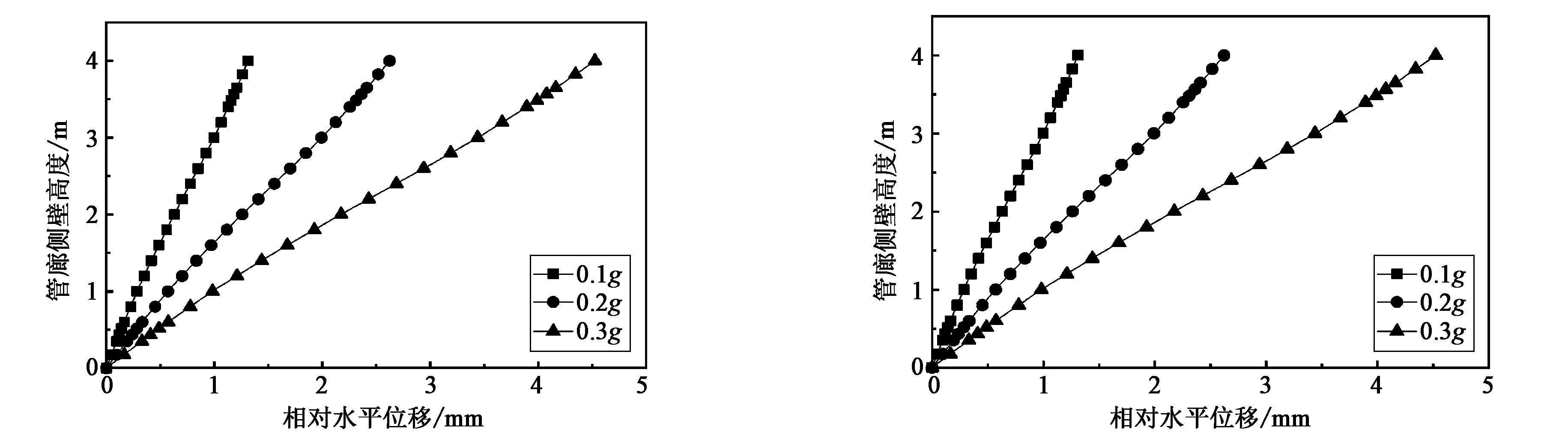
(a)左侧壁相对水平位移 (b)右侧壁相对水平位移图6 不同强度Kobe波作用下管廊侧壁相对水平位移

2.1.3 应力响应

不同强度的Kobe波作用下管廊结构的第一主应力S11与第三主应力S33的应力云图如图7—图9所示，不同强度Kobe波作用下S11与S33应力对比图如图10所示。由图7—图10看出：

(1)在横向地震波作用下，管廊结构主要承受横向地震力作用，其第一主应力云图较为明显，在0.1gKobe波作用下，第一主应力最大值为327 kPa，在过程中也会产生竖向方向的应力，其最大值为-325 kPa,对结构的影响稍逊于水平向。

(2)随着地震动强度的增强，结构应力随之增长，在横向地震作用下，其第一主应力最大值由0.1g时的327 kPa增长到0.2g时的654 kPa再到0.3g时的1355 kPa。即地震强度每增大0.1g，其第一主应力值提高一倍。

(3)根据应力云图可以看出，在横向地震作用下，管廊在腋角周围处应力较为集中，且顶底板处应力分布会比侧壁处应力分布较为集中，该现象随地震动的强度增大而愈加明显，这意味着在强地震作用下，管廊结构的腋角周围处与顶底板会先于管廊侧壁处破坏。

(a)S11应力云图 (b)S33应力云图 (a)S11应力云图 (b)S33应力云图 图7 0.1g Kobe波下S11与S33应力云图 图8 0.2g Kobe波下S11与S33应力云图

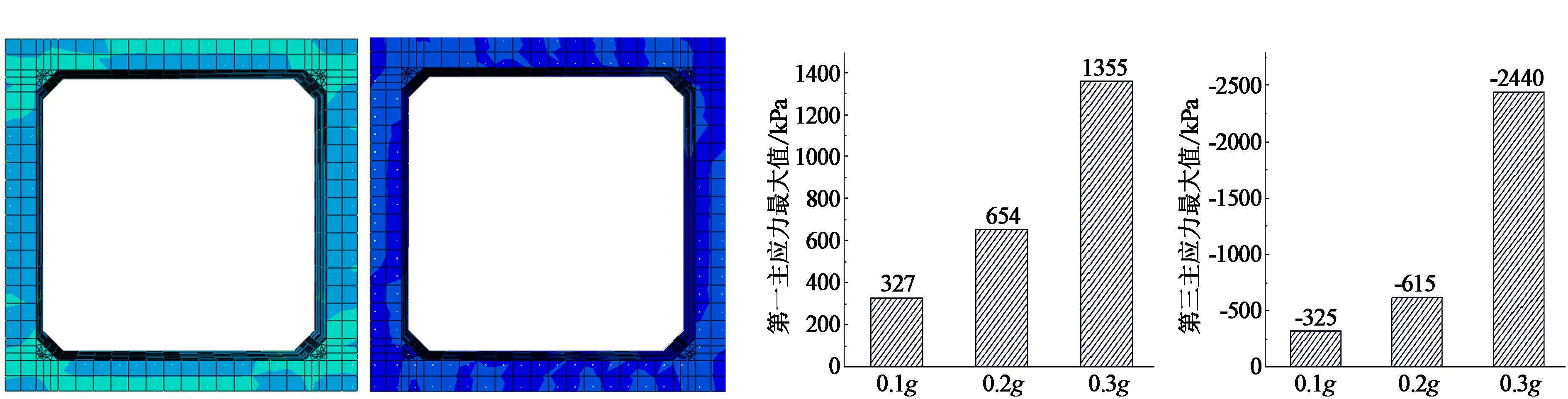
(a)S11应力云图 (b)S33应力云图 (a)S11应力对比图 (b)S33应力对比图图9 0.3g Kobe波下S11与S33应力云图 图10 不同强度Kobe波下应力对比图

2.1.4 接头响应

不同强度Kobe波作用下两节管廊接头间横向错动位移时程如图11所示。由上述接头横向错动位移时程图可知：在横向地震作用下，预制管节间的接头会产生横向错动位移，且随着地震动强度的增大，错动位移随之增大，其中在0.3gKobe波作用下产生的峰值接头错动位移为1.3 mm。

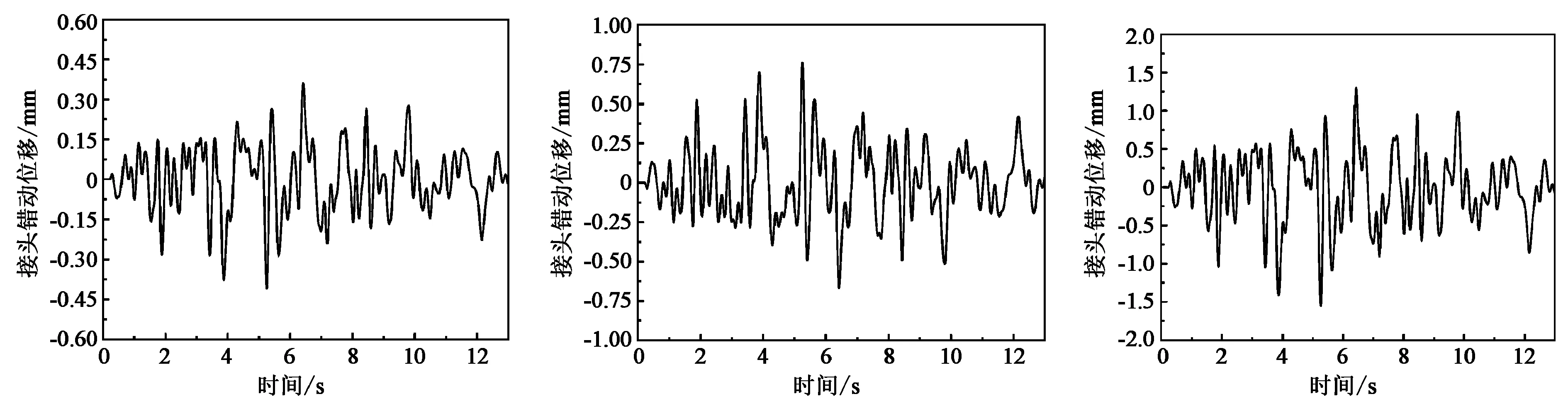
(a)0.1g (b)0.2g (c)0.3g 图11 不同强度Kobe波作用下接头横向错动位移时程图

2.2 地震波频谱

由于地震波之间存在着频谱差异，在以往的工程经验可知，当外界振动频率与结构的自振频率相近时，会发生共振导致结构破坏加剧，这足以说明地震波频率对结构的影响，为了进一步探究不同频谱的地震波对预制节段拼装管廊的地震响应[14]，本文选取了3条地震波，分别是Kobe波、Imperial_vally波和Northridge波，同样从加速度响应、位移响应、应力响应以及接头响应4个方面分析这3种波作用下的结果。

2.2.1 加速度响应

3种不同频谱地震波作用下土体底部及管廊底部加速度时程曲线如图12所示。

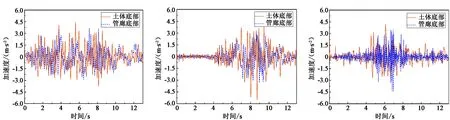
(a)Kobe波 (b)Imperial_vally波 (c)Northridge波图12 3种不同频谱地震波作用下土体底部及管廊底部加速度时程曲线

根据时程曲线可以看出：

(1)地震波频谱在土体传递过程中不会发生畸变，且传递至管廊结构时，依然保持固有频率，这种特性在不同频率下的地震波都具有；管廊结构底板处加速度时程与输入波加速度时程波形一致，但因其向上传播过程中存在着时间差而致使管廊结构底板处加速度波形稍显滞后。

(2)3种地震波作用下，土底加速度峰值均大于输入波加速度峰值，其中Kobe波作用下，土体加速度峰值为4.44 m/s2是输入时3.69 m/s2的1.2倍；Imperial_vally波作用下为1.28倍；Northridge波为1.20倍。说明土体对不同频率地震波均有放大作用，其原因系地震波向上传递过程中发生反射与先前地震波叠加造成。

2.2.2 位移响应

3种波作用下，管廊侧壁相对水平位移如图13所示。

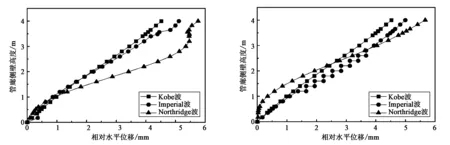
(a)左侧壁相对水平位移 (b)右侧壁相对水平位移图13 3种不同频谱地震波作用下的侧壁相对水平位移

由图可知：

不同频率地震波作用下，管廊侧壁相对水平位移随管廊高度的增高而增大，如在Kobe波作用下，管廊侧壁高为2 m时的相对水平位移为2.175 mm，而当管廊侧壁高为4 m时，相对水平位移为4.523 mm。且不同频率地震波作用下，相对水平位移变化存在着差异，该差异与侧壁加速度分布的差异有着密切的联系。

不同频率地震波作用下，管廊结构都会产生轻微的偏转，即随着地震动震荡，且震荡大小随地震波波谱的改变而改变，当地震波频率与结构的频率相接近时便会产生共振，此时震荡的大小处于峰值。

2.2.3 应力响应

图14为不同频率下的地震波第一主应力与第三主应力对比图，由图可初步得出如下结论：

同强度不同频率地震波作用下，结构应力响应不一。且在不同频率的横向地震作用中，结构的水平向影响大于竖向影响。

不同频率的横向地震波作用下，管廊结构在腋角四周及顶底板的应力分布比其他地方较为集中，其中Kobe波的影响相对其他两条地震波的影响较为显著，Kobe波作用下管廊的第一主应力为1355 kPa，第三主应力为-1533 kPa，均大于Imperial_vally波的977 kPa和-986 kPa，以及Northridge波的632 kPa和-655 kPa。可能原因是Kobe波的频率比较接近管廊的频率从而使得共振影响大于另外两条波。

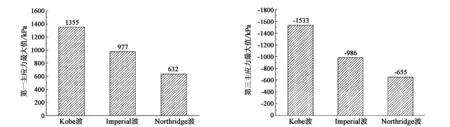
(a)S11应力对比图 (b)S33应力对比图图14 不同频率地震波作用下S11与S33应力对比图

2.2.4 接头响应

由图15不同频率地震波作用下接头相对错动位移图可得出如下分析结果。

(1)在不同频率地震作用下，预制管节间的接头会产生横向错动位移，且随着地震动波普的改变，错动位移随之发生改变，接头的峰值错动位移出现在地震波加速度峰值处，其中在Kobe波作用下产生的峰值接头错动位移较其他两种谱型的地震波大，Kobe波为1.3 mm，Imperial_vally波为0.9 mm，Northridge为1.14 mm。

(2)随着地震波频谱的改变，监测点的第一主应力及第三主应力均发生改变，其峰值均在地震波峰值处产生。测点2在Northridge波的作用下产生较大的切向应力，而测点1在Northridge波的作用下产生的切向应力较小，Kobe波与Imperial_vally波在测点1及测点2产生的切向应力相当。

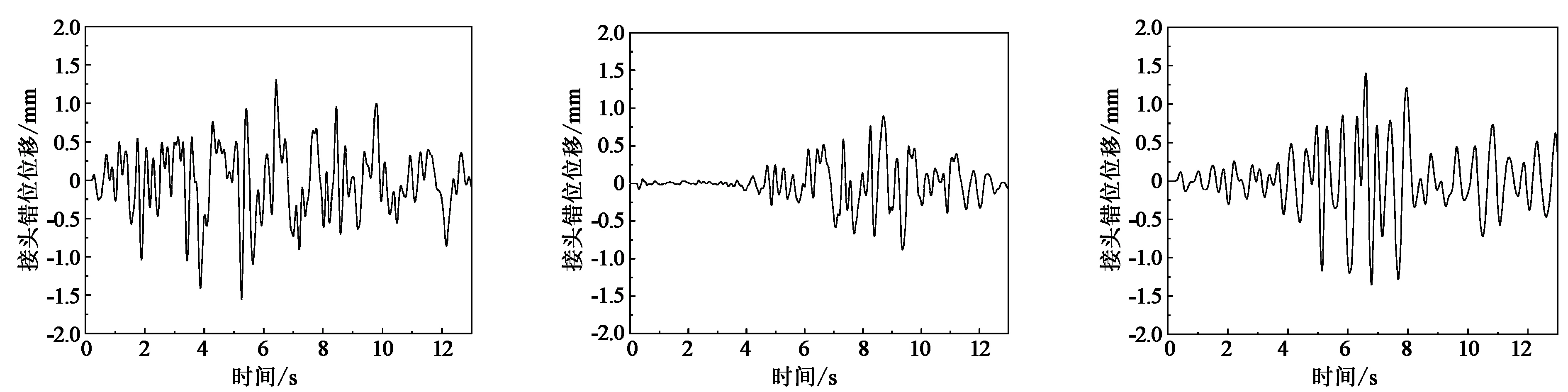
(a)Kobe波 (b)Imperial_vally波 (c)Northridge波图15 不同频率地震波作用下接头相对错动位移

2.3 双向地震动作用

实际工程中，地震作用系呈多向运动的复杂三维空间性，1995年日本阪神大地震致使大开地铁车站的塌毁也引起众多国内外学者的重视及研究，其中杜修力在对大开地铁站的抗震模拟中也得出了竖向地震分量对结构的地震响应起着重要的作用[15]，因此有必要针对预制节段拼装综合管廊进行双向地震动进行探讨。

文中分别设定了X向(横向)地震分析、Z向(竖向)地震分析及X+Z向(双向)地震分析3种工况[16]，地震波选用加速度幅值调整为0.1gKobe波，探讨3种工况下预制节段拼装综合管廊的位移响应、应力响应及接头响应。

2.3.1 位移响应

3种方向地震动作用下管廊结构的侧壁相对水平位移如图16所示，分析可得：

当仅输入竖向地震动时，结构产生较小的相对水平位移，管廊左右侧壁数据基本相同，最大值为0.477 mm，而横向位移为1.310 mm，大致为仅输入横向地震动时产生的相对水平位移的36.4%，这说明当仅输入竖向地震动时也会对结构产生横向作用，只是该影响程度较小。

输入双向地震动时，结构会产生较大的相对水平位移，最大值为2.26 mm，且比竖向地震与横向地震作用产生的相对位移简单相加的结果较大，说明同时输入竖向地震动与横向地震动时，对水平向响应具有放大效应。

(a)左侧壁相对水平位移 (b)右侧壁相对水平位移图16 管廊侧壁相对水平位移

2.3.2 应力响应

图17为不同方向地震波作用下管廊第一主应力S11与与第三主应力S33应力对比图，由图可以得出：

仅输入横向地震波时，其水平向影响较大，竖直向影响较小，水平向第一主应力最大值为327 kPa，竖向第三主应力为-325 kPa；仅输入竖向地震波时，其水平向影响较小，竖直向影响较大；当输入双向地震动时，结构水平向及竖向的响应均较大，水平向为383 kPa，竖向为-363 kPa。

(a)S11应力对比图 (b)S33应力对比图图17 不同方向地震波作用下S11与S33应力对比图

根据应力云图(略)可以看出，无论是横向作用、竖向作用、还是双向作用，结构的腋角四周及顶底板应力相比其他部位较为集中，且在竖向地震动的参与下，该效果愈加明显。

2.3.3 接头响应

图18和图19分别是不同方向地震波作用下的管廊接头间横向错动位移时程图与竖向错动位移时程图。

由图18和图19分析可得：仅输入横向地震波时，管廊的横向接头错动位移为0.36 mm，而仅输入竖向地震波时横向接头错动位移仅为0.08 mm，当输入双向地震动时，横向接头错动位移达到0.54 mm；仅输入横向地震波时，管廊的竖向接头错动位移为0.06 mm，而仅输入竖向地震波时横向接头错动位移为0.26 mm，当输入双向地震动时，横向接头错动位移达到0.47 mm。说明了管廊结构在双向地震动下响应会得到放大，放大倍数约为1.5倍，并非是简单作用相加。

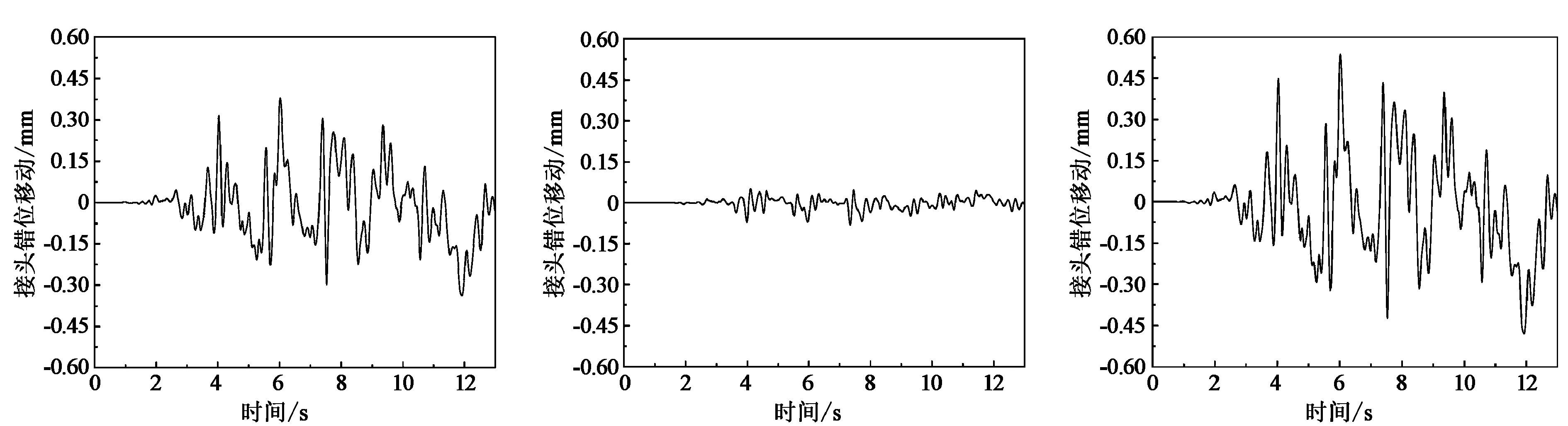
(a)X向 (b)Z向 (c)X+Z向图18 不同方向地震波作用下接头横向错动位移时程图

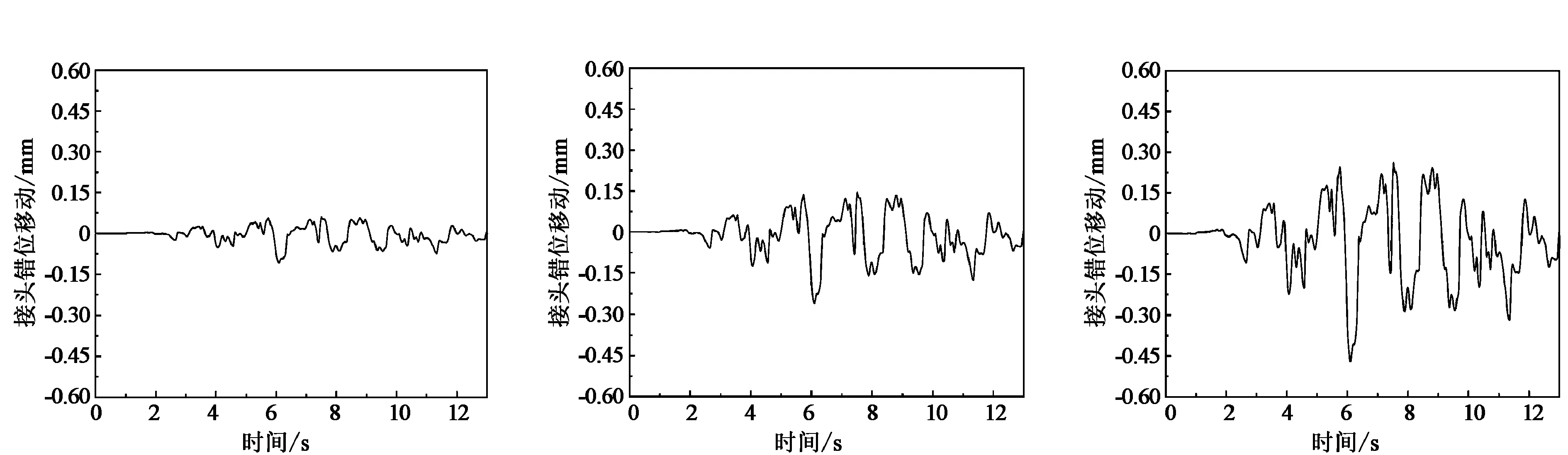
(a)X向 (b)Z向 (c)X+Z向 图19 不同方向地震波作用下接头竖向错动位移时程图

3 结论

以示例综合管廊为研究对象，建立基于三维黏弹性边界的预制节段拼装综合管廊精细化三维有限元模型，由地震动强度、地震波频谱特征、双向地震动3个方面的地震响应结果可得出以下结论。

(1)地震响应随着地震动强度的增加而增大，且在管廊的腋角四周及顶底板应力分布较为集中，同时横向地震作用下，结构会随地震动震荡并发生偏转，两个管节间亦会产生接头错动位移，因此在强地震作用下，预制管节接头可能发生大错位而对结构安全造成影响。

(2)不同地震波频谱作用下，结构的地震响应存在着差异，在Kobe波、Imperial_vally波、Northridge波调整至同等峰值强度作用下，Kobe波对结构产生的响应最大，因此，在今后进行结构抗震分析中，应尽可能多选几条不同频谱的地震波，以取得结构最大的地震响应，防止由于地震波卓越频率与结构自振频率差别太大造成的被动保守估值。

(3)在进行双向地震动时，由于竖向地震力的参与，相较于单向地震力输入，结构的响应会被放大，放大倍数约为1.5倍，而不是简单的结果相加，因此在日常的抗震计算中，应考虑竖向地震动的参与以取得更加贴近实际的结果。