基于主成分和聚类分析的汽车行驶工况构建

徐宗煌, 林 瑶

(1.福州理工学院 应用科学与工程学院,福建 福州 350506; 2.福州大学 环境与资源学院,福建 福州 350108)

本文的问题和数据均源于2019年“华为杯”第十六届中国研究生数学建模竞赛D题．汽车行驶工况(Driving Cycle)又称车辆测试循环工况,是指汽车在行驶过程中具有代表性的速度-时间关系曲线．由于该曲线能够反映汽车道路行驶的运动学特征[1],是汽车行业的一项重要的、共性基础技术,也是汽车各项性能指标标定优化时的主要基准．因此,基于国内汽车行驶的工况特点和规律,构建出适合我国国情的汽车行驶工况曲线具有的重要的经济意义和实用价值[2]．

目前,许多汽车发达国家均已开发了适合实际情况的汽车行驶工况,早在20世纪50年代,美国就制定了世界上第一个汽车行驶工况标准,之后欧洲部分国家、日本等,陆续颁布了具有代表性的典型汽车行驶工况[3]．现阶段,国内外构建汽车行驶工况的方法主要有短行程法[4—5]、小波变换法[6]、聚类分析法[7—9]及马尔可夫分析法[10]．本文基于城市汽车实际道路行驶采集的数据,通过对时间不连续数据、尖点数据、毛刺噪声数据以及怠速异常数据进行一系列预处理,结合主成分和K-means聚类分析法,对汽车行驶工况进行构建并分析误差．

1 数据预处理

1.1 研究思路

原始数据中不良数据的存在,会严重影响后续工作的结果,而数据预处理的方法有很多种,对不同类型的数据,其处理方法也不尽相同．因此,设计合理的方法对不良数据依次进行预处理显得尤为重要,从而使得预处理后的数据能够反映汽车的真实行驶情况,为后续运动学片段的提取以及汽车行驶工况的构建做准备.汽车道路行驶数据预处理的流程图见图1．

图1 数据预处理流程图

1.2 预处理过程

1.2.1时间不连续数据处理 对于时间不连续数据的处理,关键在于如何定义短时间丢失和长时间丢失两种情况的临界时间,考虑一般汽车经过隧道的情况,不妨定义临界时间为我国公路隧道平均长度与城市汽车平均行驶速度之比,即

(1)

式中:τ为临界时间;L为我国公路隧道平均长度,由我国公路隧道长度L′与隧道数量N的比值确定,即

(2)

查阅资料有L′=14 039.7 km,N=15 181;V为城市汽车平均行驶速度,查阅资料可知V=40 km/h．

由 (1)式和(2) 式,可得

因此,不妨取临界时间为τ=85 s,则认为τ>85 s属于“车速冻滞带”,不进行插值补全;而2≤τ≤85为数据短时间丢失,采用线性插值法进行平滑处理,即

(3)

式中:(t1,v1)和(t2,v2)为短时间缺失的两个相邻时间GPS车速对应的坐标点;t为缺失的时刻;v为缺失的时刻要插入的速度值．

分别对文件1～文件3的原始数据进行时间不连续数据处理,可得到3个文件经过处理后增加的记录数(表1)．

表1 时间不连续数据处理过程记录

1.2.2尖点数据处理 由已知普通轿车一般情况下0～100 km/h的加速时间大于7 s,可知其最大加速度

而紧急刹车最大减速度为7.5～8 m/s2,不妨令最大减速度为

dmax=7.5 m/s2.

随后,经多次采用线性插值法进行平滑处理,使得汽车加、减速度处于下式的正常范围:

(4)

由于采集数据的采样频率为1 Hz,则线性插值公式为

(5)

式中:vxt为第t个时刻的GPS车速数据修正后的值;vt-1和vt+1分别为第(t-1)和第(t+1)个时刻的GPS车速数据．

分别对文件1～文件3的原始数据进行尖点数据处理,可得到3个文件处理的过程记录(表2)．

表2 尖点数据处理过程记录

值得注意的是:文件3中会出现异常的GPS速度,而导致汽车加、减速度异常的情况,即GPS速度已超出实际情况的车速数据．本文以高速公路上行驶最高限速120 km/h为标准,舍弃GPS车速大于120 km/h的数据．由此可得文件3中删除的数据记录数为345．

1.2.3毛刺噪声数据处理 由于可按怠速情况处理毛刺噪声数据,因此需要对GPS车速数据进行修正,以反映汽车的真实行驶工况．查阅资料[11]可知,最终的怠速修正上限为v0=10 km/h,线性修正上限为15 km/h,即可得修正公式

(6)

通过(6)式对原始数据进行修正,可得毛刺噪声数据处理过程记录(表3)．

表3 尖点数据处理过程记录

1.2.4怠速异常数据处理 对于怠速异常数据情况，保留180 s的数据，直接将怠速时间大于180 s的数据删除即可.经过统计，可得怠速异常数据处理的过程记录(表4).

1.3 预处理结果

经过上述对原始数据预处理，可得到文件1～文件3各文件数据经预处理后的记录数(表5).

表5 数据预处理后的记录数

2 基于主成分和聚类分析的汽车行驶工况构建

2.1 研究思路

按照图2的研究思路,首先,基于预处理后的数据,对运动学片段进行划分[12],考虑到所选取汽车运动特征评估体系指标合理性,同时引入14个相关的运动特征指标;其次,由于选取的指标较多,可能某些指标之间相互存在信息重叠的现象,因此采用主成分分析对运动特征指标进行降维处理,通过将较多的指标转化为几个主要成分,可以大大降低分析和计算的难度;再次,选取具有代表性的5个主成分,基于K-means聚类分析算法将运动学片段,按照拥堵路况、一般拥堵路况和通畅路况分为3类,再根据聚类结果选取最优工况片段,同时以总时间1 200～1 300 s为要求进行组合,从而得到最终的工况曲线;最后,对汽车行驶工况与该城市所采集数据源(经处理后的数据)的各指标(运动特征)值进行误差分析,分析所构建的汽车行驶工况的合理性[13]．

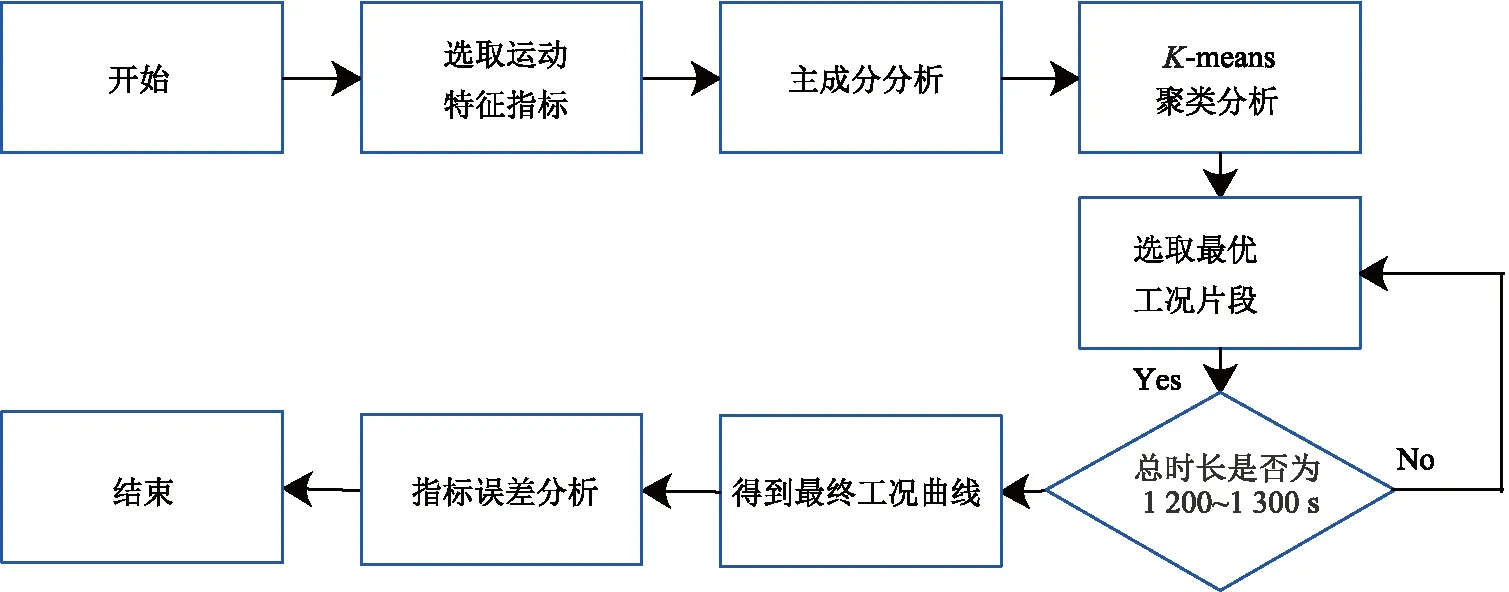
图2 汽车行驶工况构建的主要思路图

2.2 运动学片段的划分

2.2.1划分条件 由于一个完整的运动学片段包含了怠速、加速、减速以及匀速4个状态,而如果持续时间小于20 s,那么认为该片段汽车处于频繁启动的状态,则该片段可能不能刻画出该时间段汽车的行驶工况．因此,为了避免这种情况发生,认为运动学片段的持续时间应当大于等于20 s;且将小于20 s的片段与其后一个片段合并为一个新的片段,直至合并成新片段的持续时间大于等于20 s,即认为构成了一个完整的运动学片段[14]．

2.2.2划分结果 利用MATLAB编程,根据划分条件对预处理后的数据进行进一步的划分,可得到文件1～文件3各文件的运动学片段数量记录(表6)．

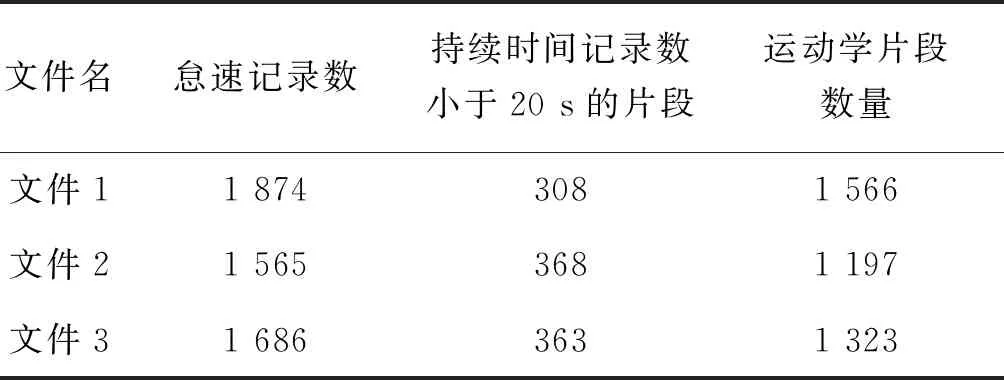
表6 各文件的运动学片段数量记录

2.3 指标选取及计算

显然GPS车速原始数据中,最直观的两个汽车运动特征的指标为时间和速度,而加速度和减速度则可由时间和速度计算得到;如果只采用这4个指标描述汽车行驶工况,则可能会造成汽车行驶特征信息的丢失,不能真实、全面地反映其行驶工况．因此，需要引入以下运动特征指标[15]．

1)运行时间

t=tt

，

(7)

式中:tt为运动学片段的总时间,即数据的总个数．

2)最大速度vmax

vmax=max{vi,i=1,2,…,tt}.

(8)

3)平均速度vm

(9)

式中:s表示运动学片段的运行距离,即该片段的距离之和．

4)平均行驶速度vmr.平均行驶速度为除了怠速外的平均速度，即

(10)

5)速度标准差Sv

(11)

6)加速度ai,i+1

(12)

式中:ai,i+1为第i秒到第(i+1) 秒的瞬时加速度;vi为第i秒的GPS车速;ti为第i秒．

7)最大加速度amax

amax=max{ai,i=1,2,…,tt}，

(13)

式中:tt表示运动学片段的总时间,即数据的总个数．

8) 平均加速度am

(14)

9) 加速度标准差Sa

(15)

10) 最大减速度vd,max

vd,max=max{vi,i=1,2,…,tt}.

(16)

11) 平均减速度vd,m

(17)

12) 怠速时间比例Pi

(18)

式中:ti表示运动学片段中ai>0.1 m/s2的时间．

13) 加速时间比例Pa

(19)

式中:ta表示运动学片段中vi=0的时间．

14) 减速时间比例Pd

(20)

式中:td表示运动学片段中ai<-0.1 m/s2的时间．

15) 匀速时间比例Pe

(21)

式中:te=t-ti-ta-td为运动学片段中匀速的时间．

结合以上分析,由于文件1～文件3为同一辆车在不同时间段所采集的数据,因此,先将文件1～文件3整合成新的数据,利用MATLAB编程,可得到各运动学片段运动特征评估体系指标值(表7)．

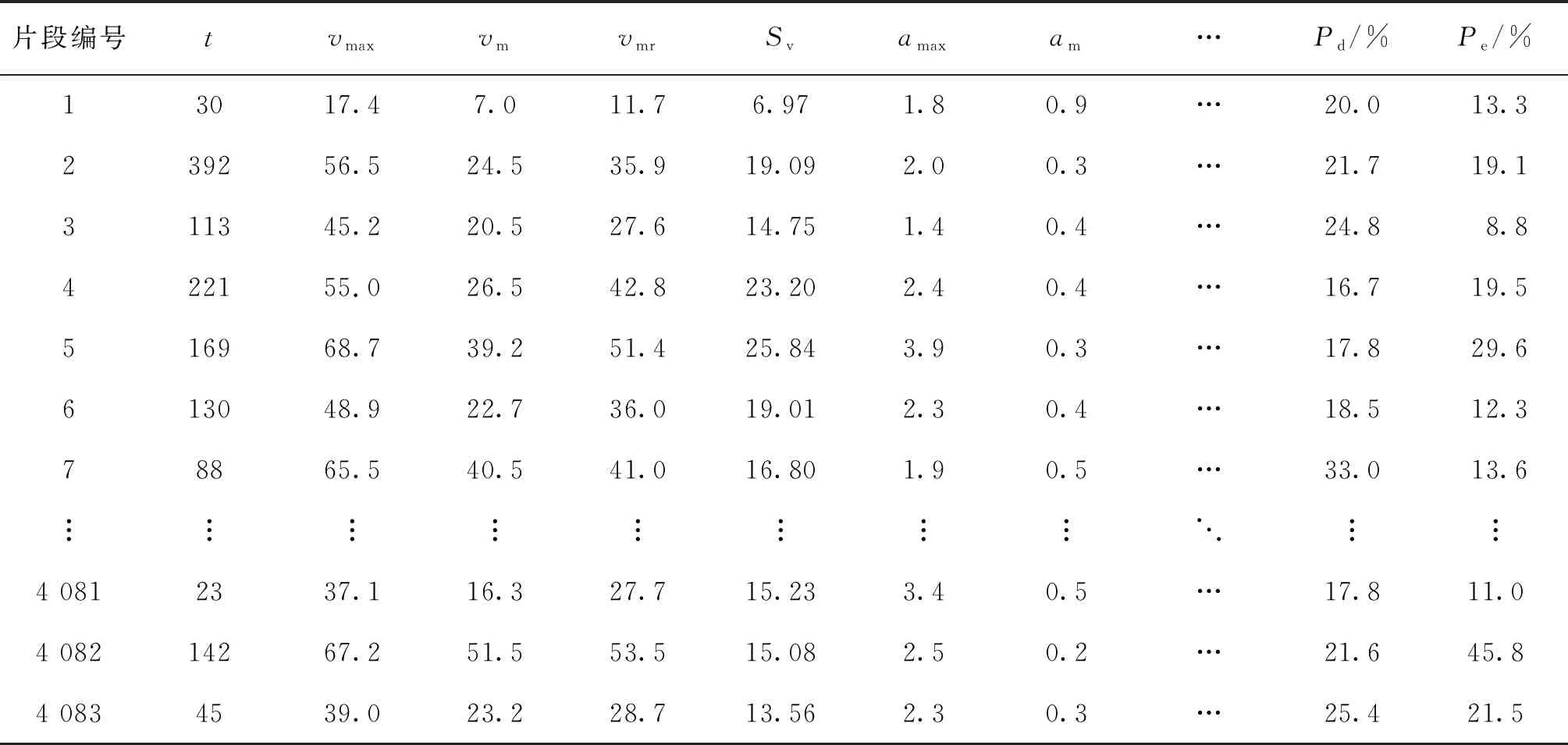
表7 各运动学片段运动特征评估体系指标值

2.4 主成分分析

上述选取的指标较多，由于某些指标之间可能存在信息重叠的现象，因此采用主成分分析对运动特征指标进行降维处理.主成分分析[16—17]是在处理多个指标时对指标进行降维的一种方法，其基本思想是将相互之间具有一定关联性的多个指标，转化为几个互相无关的主要成分(即综合指标)，可以大大降低分析和计算的难度.采用主成分分析对运动特征评估体系指标进行降维分析的具体算法描述见表8[18].

表8 各文件的运动学片段数量记录

利用MATLAB编程进行主成分分析,计算可得各运动特征指标按从大到小排列的贡献率,见表9．由表9可以看出,前5个特征根的累计贡献率已经接近90%,表明主成分分析效果很好.因此,可以认为,前5个主成分已经包含了14个运动特征指标的大部分信息,即可选取前5个主成分进行综合评价．前5个主成分对应的特征向量见表10．

表9 主成分分析各指标贡献率

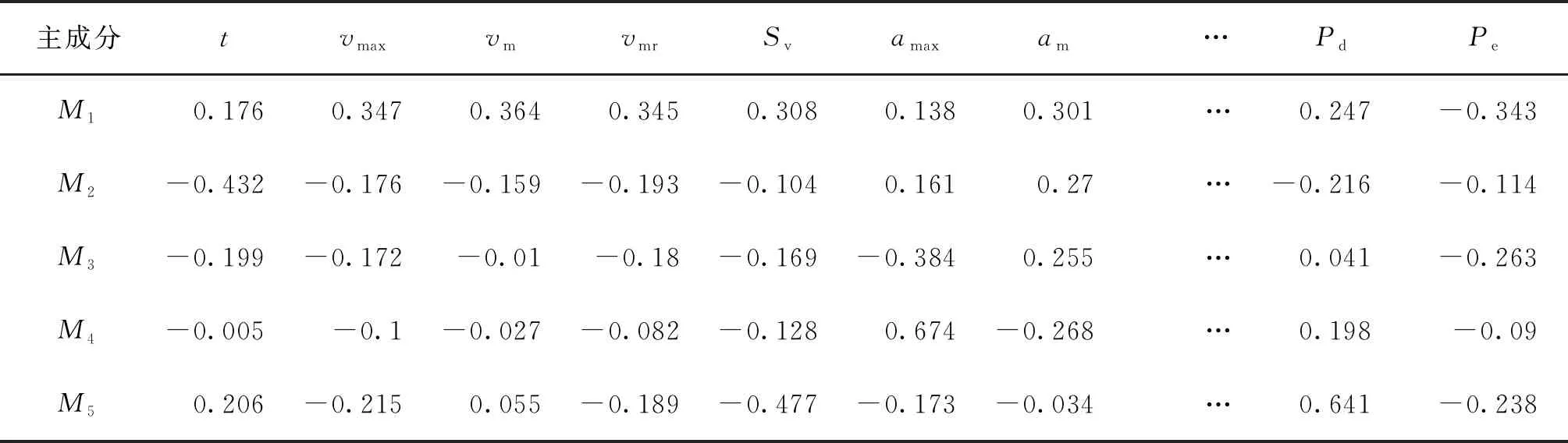
表10 标准化变量的前5个主成分对应的特征向量

2.5 聚类分析

考虑到一个路段往往包含了不同的路况类型,将每个运动学片段按照拥堵路况、一般拥堵路况和通畅路况分为3类路况类型[19].将具有相同路况的运动学片段分为一类,同时可将选取的3类路况类型的片段组合成能体现汽车行驶特征的汽车工况曲线．

基于上述主成分分析所选取的5个主成分数据,采用K-means聚类分析算法对运动学片段进行分类,该类算法是著名的划分聚类算法[20—22]．该算法由于其简洁和高效,成为所有聚类算法中最广泛使用的聚类算法,其核心思想是把n个数据对象划分为K个聚类,使每个聚类中的数据点到该聚类中心的平方和最小．显然,可以根据路况类型采用K-means聚类将运动学片段分为3类,其具体的算法描述见表11．

表11 K-means聚类算法描述

2.6 汽车行驶工况曲线的构建

经过上述分析,利用MATLAB 编程,对5个主成分进行K-means聚类分析可得到分类结果(表12)．

表12 各文件的运动学片段数量记录

由表12可知,3类工况运动学片段数比例约为

拥堵工况∶一般拥堵工况∶通畅工况=3∶6∶1.

因此,从第1类选取聚类偏差度最小的前3个运动学片段,从第2类选取聚类偏差度最小的前6个运动学片段,从第3类选取聚类偏差度最小的1个运动学片段,同时以总时间1 200～1 300 s进行组合,总共选取了10个运动学片段(表13)．

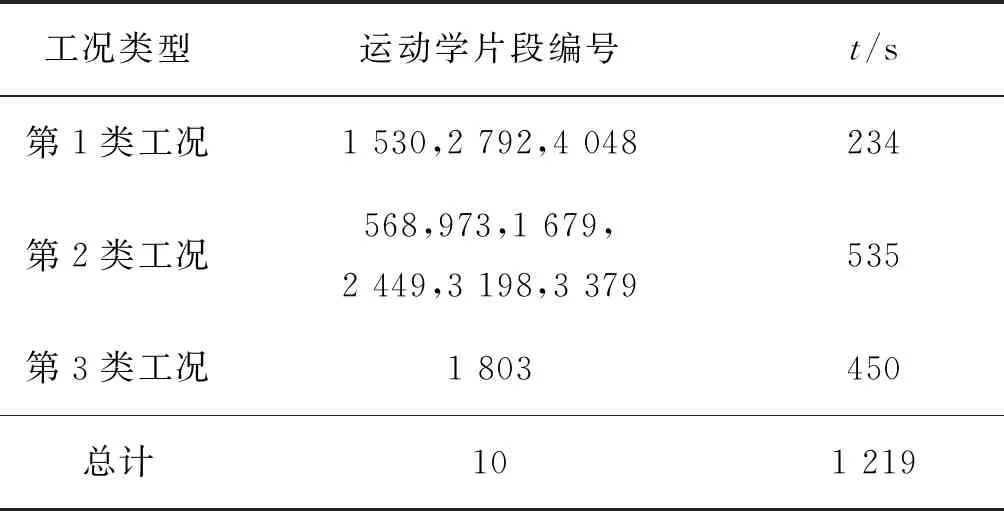
表13 各文件的运动学片段数量记录

最终得到的工况曲线见图3.

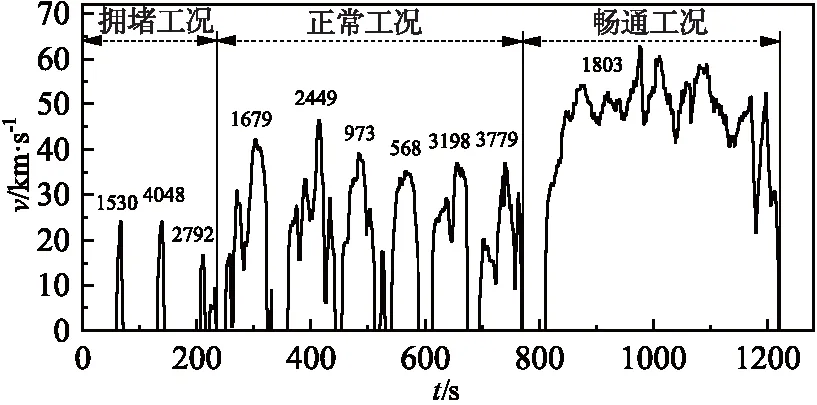
图3 汽车行驶工况曲线

2.7 指标误差分析

为了分析上述所构建的汽车行驶工况的合理性,需要对汽车行驶工况与该城市所采集数据源(经处理后的数据)的各指标(运动特征)值进行误差分析[19]．不妨令

(22)

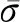
由 (22) 式计算可得到误差分析统计表(表14)．

由表14可以看出,汽车行驶工况与该城市所采集数据源(经处理后的数据)各指标的最大相对误差为平均减速度的误差σi max=17.20%.最终构建的汽车行驶工况,除了匀速时间比例、平均加速度以及怠速时间比例大于10%,其余运动特征指标与该城市所采集数据的相对误差均小于10%．这表明,上述所构建的汽车行驶工况曲线是有效的,完全能够体现参与数据采集汽车行驶特征的汽车行驶工况曲线,这验证了所构建的汽车行驶工况的合理性．

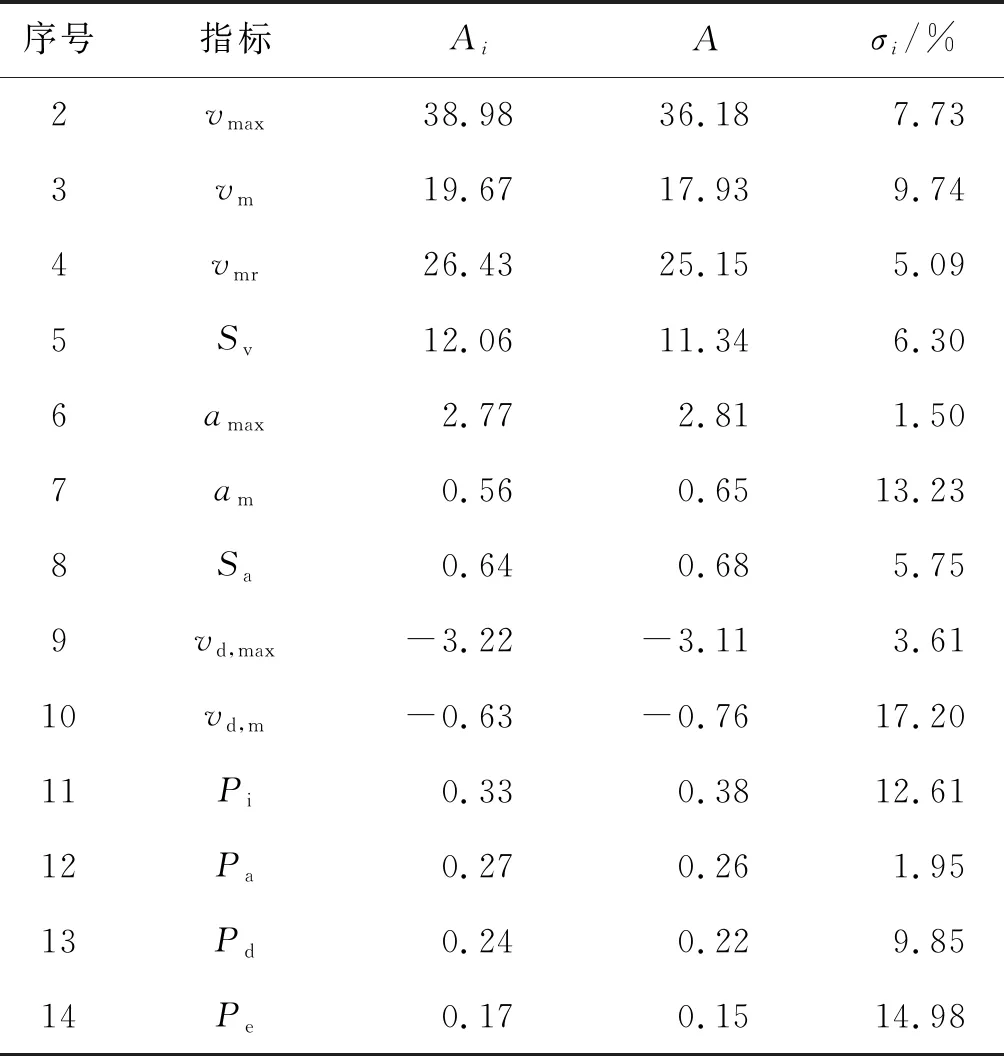
表14 运动特征指标误差分析统计表

3 结语

本文给出了汽车行驶的工况特点和规律,基于城市汽车实际道路行驶采集的数据,通过对数据进行时间不连续数据、尖点数据、毛刺噪声数据以及怠速异常数据一系列预处理.采用主成分分析对运动特征指标进行降维处理,通过将较多的指标转化为几个主要成分,可以大大降低分析和计算的难度．最终,结合主成分和K-means聚类分析,构建了能客观真实地反映汽车行驶特征的工况曲线．经过汽车行驶工况与该城市所采集数据源(经处理后的数据)的各指标(运动特征)值的误差分析,验证了所构建的汽车行驶工况的合理性．