教育扩张、劳动参与率与经济增长

孙志军，管 振

北京师范大学 经济与工商管理学院、首都教育经济研究院，北京 100875

引 言

教育投资的直接经济价值可以从两个角度来探讨：对提高个体工资收入的作用和对国家或地区经济增长的贡献(1)A. B. Krueger and M. Lindahl,“Education for Growth: Why and for Whom”, Journal of Economic Literature, 2001, 39(4), pp.1101-1136.。对于前者，人们普遍的做法是使用基于微观数据的明瑟收入函数估计教育的个人收益率(2)李实、张钰丹：《人力资本理论与教育收益率研究》，《北京大学教育评论》，2020年第1期。；对于后者，往往是依据经济增长理论，将教育变量纳入到增长模型中，采用宏观层面的数据进行分析(3)杜育红、赵冉：《教育对经济增长的贡献——理论与方法的演变及其启示》，《北京师范大学学报(社会科学版)》，2020年第4期。。基于明瑟收入函数的微观研究揭示了其他条件相同的情况下，个体多接受一年教育，收入会提升百分之多少。相关的研究文献虽然已汗牛充栋，但是此方法还存在着一些不足。首先，教育存在着导致技术进步、社会稳定与安全、公共事务参与效率提升等的外部性(4)W. W. McMahon,“An Analysis of Education Externalities with Applications to Development in the Deep South”, Contemporary Economic Policy, 2007,25(3), pp.459-482.，未接受或接受较少教育的群体能够分享接受较多教育群体带来的经济收益，外部性的存在使得明瑟收益率会低估教育的经济价值。其次，明瑟收益率中包含了教育的“信号效应”所带来的收入提升，而这种效应不代表个体劳动生产率的提升(5)M. Spence,“Job Market Signaling”, Quarterly Journal of Economics, 1973, 87(3), pp.355-374.，因而，可能会高估教育的经济价值。依据宏观层面数据的研究主要是基于生产函数，分析劳动力群体的平均教育水平对经济总产出或人均产出的影响，一定程度上可以弥补微观研究的这些不足。利用加总的收入数据进行分析，使得在微观数据中隐藏的教育外部收益得以体现。同时，由于教育通过人力资本积累来影响经济产出，没有生产力提升作用的信号效应将不会显现出来。基于上述考虑，本文从宏观方面探讨教育的经济价值。

国内虽已有大量的文献从宏观方面探讨我国教育与经济增长的关系，但是还存在一些不足。其中一个是没有考虑由于教育扩张会延缓个人进入劳动力市场的时间，从而降低劳动参与率。从图1可以发现，伴随着大学入学率的提升，我国的劳动参与率逐年下降。具体来看，大学入学率从1995年的不到5%提升到2018年的50%以上。但是15-24岁群体的劳动参与率从1995年的75%以上下降到2018年的约45%。受此影响，这20多年间15-64岁群体的劳动参与率下降了约8%。根据《中国统计年鉴2019》的数据，2018年我国15-64岁群体约10亿人。劳动参与率下降8%，意味着与以前相比，高达8000万人没有进入劳动力市场。因之，教育扩张虽然提升了劳动力质量，提高了劳动力的人均收入，但是因为总人口人均收入水平既取决于劳动力人均收入，又取决于劳动参与率，使得教育扩张对总人口人均收入的影响具有不确定性。针对这一不足，在理论分析上，本研究把劳动参与率引入到增长模型中，解释教育扩张对总人口人均收入的影响，并结合中国的现实参数，模拟不同的条件下两者之间的数量关系。另一个重要的不足是，大多数文献仅仅考虑到教育对人力资本积累的促进作用，忽略了教育的正外部性，这将会低估教育的经济价值。针对这一点，本研究把教育的外部性引入到增长模型中，分析教育扩张对经济增长的影响。

图1 中国1995—2018年的劳动参与率和大学入学率数据来源：根据世界银行《世界发展指标》数据绘制。

除了研究内容外，在从宏观层面探讨教育对经济增长的研究方法中，也存在一些不足。已有的实证模型常常使用双对数形式，在这种情况下教育变量的系数反映了产出弹性，与微观明瑟收益率难以进行比较(6)J. Benhabib and M. M. Spiegel,“The Role of Human Capital in Economic Development Evidence from Aggregate Cross-country Data”, Journal of Monetary Economics, 1994, 34(2), pp.143-173.。为了克服这个困难，我们转向采用宏观明瑟方程，从而在方法上将微观和宏观结合起来。宏观明瑟方程最基本的特征是采用半对数形式，教育变量的系数又称为宏观明瑟收益率，其含义为劳动人口平均受教育年限增加一年，劳动力人均收入提升百分之多少(7)J. Heckman and P. Klenow, Human Capital Policy, Chicago: Chicago University Press, 1997, pp.13-16.。国外有些学者用此模型估计得到了较高的收益率(8)D. Cohen and M. Soto,“Growth and Human Capital: Good Data, Good Results”, Journal of Economic Growth, 2007, 12(1), pp.51-76；R. J. Barro and J. W. Lee,“A New Data Set of Educational Attainment in the World, 1950-2010”, Journal of Development Economics, 2013, 104, pp.184-198.；也有研究得到了较低的收益率(9)B. Sianesi and J. V. Reenen,“The Returns to Education: Macroeconomics”, Journal of Economic Surveys, 2003, 17(2), pp.157-200；A. Bassanini and S. Scarpetta,“The Driving Forces of Economic Growth”, OECD Economic Studies, 2001,(2), pp.9-56.。为什么估计结果出现较大的差异？在方法上，教育的测量误差，以及模型遗漏诸如教育质量等变量可能是其原因。在理论上，像前文所说，外部性和信号理论一定程度上可以解释宏观明瑟收益率高于或低于微观明瑟收益率。在国内也有少数文献用该模型基于中国的数据进行了研究，比如李锋亮和袁本涛应用此模型的研究发现教育与经济发展水平存在显著的正向关系，但是他们没有与微观收益率进行比较(10)李锋亮、袁本涛：《研究生教育与我国经济增长的匹配关系》，《北京大学教育评论》，2013年第3期。。为此，本文借助宏观明瑟方程，考察我国劳动力人均受教育年限对劳动力人均收入的影响，同时与微观收益率进行比较，分析我国宏观教育收益率中的人力资本积累效应和外部性的大小。

综上所述，本文的边际贡献主要体现在以下三个方面：首先，在理论上分析了教育扩张通过与劳动参与率的相互作用，对总人口人均收入的影响，并根据我国的宏观经济条件，模拟两者之间的数量关系。其次，在增长方程中，引入了教育的外部性用于解释教育扩张对经济增长的影响机制。最后，本文扩展了宏观明瑟方程在我国的应用，使得宏微观教育收益率易于比较和分析。

一、教育扩张对人均收入的影响路径

尽管经济中的总产出由劳动力创造，但是劳动力仅占总人口的一部分，劳动力人均收入和总人口人均收入具有不同的内涵(11)按照经济核算的原理，在某一时期，经济体各部门的总产出等于国民总收入。故本文对总产出和总收入将不加以区分。。因此，在本节我们首先从理论上分析教育扩张对劳动力人均收入水平的影响，然后在考虑了教育扩张对劳动参与率的挤出作用后，分析教育扩张与总人口人均收入水平的关系。

根据一般的索罗模型，技术进步是外生的(12)R. M. Solow,“A Contribution to the Theory of Economic Growth”, Quarterly Journal of Economics, 1956, 70(1), pp.65-94.。当经济达到稳态后，人均收入将以技术进步率的速度增长，教育对经济增长没有起到解释作用。Schultz把“索罗残差”解释成劳动生产率的增长，而教育被认为能够提升劳动生产率，从而在教育与经济增长之间建立起了联系(13)T. Schultz, The Economic Value of Education, New York: Columbia University Press, 1963, p.32.。Uzawa进一步把教育作为附加和单独的投入引入到增长方程中，并且假定技术进步来源于教育的发展(14)H. Uzawa,“Optimum Technical Change in an Aggregative Model of Economic Growth”, International Economic Review, 1965, 6(1), pp.18-31.。遵循他们的思想，我们把教育看作人力资本的投资形式和技术进步的来源，来考察教育扩张与经济增长的关系。

(一)基本假设

假设在任何时刻，经济体拥有一定量的物质资本、人力资本和技术，这些因素被结合起来生产产品。生产函数为柯布-道格拉斯形式，即：

(1)

其中Yt、Kt、Ht和At分别表示经济体在第t期的总产出、物质资本、人力资本和技术水平。假设人力资本存量Ht不但取决于劳动力数量Lt，也取决于劳动力质量(这里由教育水平衡量)。劳动力的教育水平来源于早期的教育扩张，且每个劳动力都接受E年的教育。则经济中总的人力资本存量可以表示为：

Ht=Lth(E)=LteρE(ρ>0)

(2)

其中，h(E)表示单个劳动力的人力资本存量，ρ衡量了教育对人力资本积累的贡献率，即每增加一年的教育，劳动力的人力资本水平提升的百分比。假设劳动力数量以外生n的速率增长，物质资本积累取决于经济体中新的投资(储蓄)减去折旧；因此，物质资本积累的动态方程为：

(3)

其中，s和δ分别表示储蓄率和折旧率。遵循Lucas的思想，假设技术水平At取决于劳动力的平均教育水平，这意味着教育存在促进技术进步的外部性(15)R. E. Lucas,“On the Mechanics of Economic Development”, Journal of Monetary Economics, 1988, 22(1), pp.3-42.。技术水平的表达式为：

At=A0eωE(ω>0)

(4)

其中A0为常数，表示当劳动力教育水平为0时，经济中技术水平的大小。ω衡量了教育对技术水平的贡献率，假设其大于0，意味着劳动力平均教育水平越高的地区，技术水平也越高。可以发现，如果令ρ=ω=0，则(1)式变为一般的索罗模型形式，因此可以把索罗模型看作此模型的一个特例。

(二)教育扩张和劳动力人均收入

结合(1)、(2)、(3)和(4)式，可得稳态时劳动力人均收入为(16)限于篇幅，理论分析中的公式推导过程未予以呈现。感兴趣的读者可向作者索取。：

(5)

从(5)式可以看出，由教育扩张导致的劳动力教育水平E的上升会提高平衡增长路径上劳动力的平均收入水平。具体来看，劳动力教育水平提升1年，稳态时的收入水平提升100*(ρ+ω)%。这也意味着教育不但通过人力资本积累，也通过技术外部性提升劳动力的收入水平。

(三)教育扩张、劳动参与率与总人口人均收入

以上主要考察了教育扩张与劳动力人均收入的关系，未涉及对全部人口经济福利的分析。劳动力教育水平的提升来源于早期在校教育时间的增加。如果个人结束教育后便参加工作，则更长的在校教育时间也延缓了其进入劳动力市场的时间，从而劳动力教育水平的提升要以牺牲年轻群体的劳动参与率为代价。劳动参与率的下降会减少经济体中的劳动力数量，从而降低总收入和总人口人均收入。总的来说，教育扩张从两个方面影响经济体的总人口人均收入。一方面，通过提升劳动生产率水平h(E)和技术水平A，促进总人口人均收入的增长；另一方面，通过减少劳动力供给数量L，抑制总人口人均收入的增长。因此教育扩张对总人口人均收入的影响具有不确定性。

参考戴维·罗默的模型，把经济体中的个体区分为幼儿、在校生、劳动力和退休人员(17)﹝美﹞戴维·罗默：《高级宏观经济学》，吴化斌、龚关译，上海：上海财经大学出版社，2014年，第115-118页。。劳动力人数等于总人口数减去幼儿数、在校生数和退休人数。假设每个个体的寿命相同，均为T，退休年龄为R，幼儿在P岁开始入学并接受E年的学校教育，然后参加(R-E-P)年的工作，直到退休(E+P≤R≤T)。假设单位时间出生的人口数量Bt按照η的速率增长，则在t时期总的人口数量Nt，等于(t-T)到t时期之间出生的人口总和，即：

Nt=(1-e-ηT)Bt/η

(6)

由(6)式可以发现，t时期总的人口数量Nt和出生的人口数量Bt的增长率相同，都为η。假设个体至少参加φ(φ≤E)时间的在校教育(可看作义务教育)才可参加工作。则在t时期，劳动年龄人口数量为受教育时间超过φ且未到达退休年龄的人口总量，即：

Vt=(e-η(φ+P)-e-ηR)Bt/η

(7)

类似地，t时期的劳动力数量等于离开学校且未退休的人口总量，即：

Lt=(e-η(E+P)-e-ηR)Bt/η

(8)

结合(6)和(8)式可得，在t时期，劳动力占总人口的比例为：

Lt/Nt=(e-η(E+P)-e-ηR)/(1-e-ηT)

(9)

劳动参与率定义为劳动力数量除以劳动年龄人口总量。结合(7)和(8)式可得，在t时期，劳动参与率为：

Lt/Vt=(e-η(E+P)-e-ηR)/(e-η(φ+P)-e-ηR)

(10)

从(9)和(10)式可以发现，教育扩张降低了劳动力占总人口的比例和劳动参与率。由于n、E、T、R、P都为常数，因此从(9)式可以发现，Lt与Nt的增长率相同，即n=η。从而，对总人口数量或劳动力人口数量增长率进行假设有着相同的含义。结合(5)和(9)式，得到稳态时的总人口人均收入为：

(Y/N)*=A0e(ρ+ω)E(s/(n+δ))α/(1-α)(e-n(E+P)-e-nR)/(1-e-nT)

(11)

图2呈现了(11)式中显示的教育扩张对总人口人均收入的影响路径。可以发现，教育扩张通过两种路径影响总人口人均收入。其一，提升劳动力生产能力和技术水平，导致A0e(ρ+ω)E项上升，促进劳动力人均收入和总人口人均收入的增长；其二，通过降低劳动参与率从而降低人口中的劳动力比例，导致(e-n(E+P)-e-nR)/(1-e-nT)项下降，抑制总人口人均收入的增长。所以，在长期阶段，教育扩张可能提高或降低总人口的经济福利。那么教育扩张会提高还是降低总人口人均收入呢？

图2 教育扩张对总人口人均收入影响路径

根据(11)式对E求二阶导数为：ξe(ρ+ω)E[(ρ+ω-n)2e-n(E+P)-(ρ+ω)2e-nR]；其中，ξ=A0(s/(n+δ))α/(1-α)/(1-e-nT)>0。由于，E+P≤R，故e-n(E+P)0，即教育的宏观收益率远大于人口增长率时，二阶导数小于0。这意味着教育对总人口人均收入影响的边际收益率(以下简称边际收益率)递减。当劳动力教育水平较低时，边际收益率为正，那么边际收益率递减使得教育对总人口人均收入呈现倒U型影响，即教育扩张先提高再降低总人口人均收入。令(11)式对E求的一阶导数等于0，得出使得总人口人均收入最大时的教育扩张水平为：

E=R-P+ln(1-n/(ρ+ω))/n

(12)

从(12)式容易发现，使得总人口人均收入最大的教育扩张水平E与退休年龄呈正比，与入学年龄呈反比，与宏观教育收益率正相关，与人口增长率负相关。因此，首先，为达到更高的人均收入水平，教育扩张水平应该随着退休年龄的提高而不断提高，而且提高的比例与退休年龄的提高比例相同。其次，随着宏观教育收益率(ρ+ω)的提高，政府应该实行积极的教育扩张政策，这看起来是理所当然的。最后，随着人口增长率的提升，政府应该减少对教育的投入；反之，政府应该通过教育扩张来应对人口增长率的下降，这也与一些学者认为可通过缩短学制来应对人口增长率下降和老龄化的观点相反(18)罗淳、吴丽娟：《缩短学制：试论“人口红利”二次开发的源头施策》，《南方人口》，2020年第5期；任兵：《缩短硕士研究生学制的探索与思考》，《中国高教研究》，2005年第3期。。

二、宏观明瑟收益率的估计

前文的理论分析论证了劳动力人均教育水平与劳动力人均收入之间的正向关系。在这一节，我们将对以上推论进行实证检验。此外，如前文所述，为了使宏微观教育收益率具有可比性，本文使用宏观明瑟方程来估计劳动力人均教育水平对劳动力人均收入的影响，即教育的宏观明瑟收益率。宏观明瑟收益率也是第四节模拟教育扩张水平和总人口人均收入关系中的重要参数。

(一)计量模型

1.估计宏观明瑟收益率的模型推导

与前文的理论模型一样，假设对于地区j，生产函数为：

(13)

各变量的定义与前文相同，Yjt、Kjt、hjt、Ljt、Ajt分别表示地区j第t期总的产出、物质资本、劳动力人均人力资本、劳动力数量和技术水平。上式两边同除以Ljt，并取对数得：

ln(yjt)=αjln(kjt)+(1-αj)ln(hjt)+(1-αj)ln(Ajt)

(14)

考虑对于同一地区，资本/产出比几乎不变，意味着完全弹性的资本供给(19)A. Young,“The Tyranny of Numbers: Confronting the Statistical Realities of the East Asian Growth Experience”, Quarterly Journal of Economics, 1995,110(3), pp.641-680.。则有：

(15)

ln(yjt)=kj+ln(hjt)+ln(Ajt)

(16)

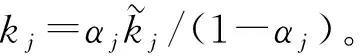
(17)

其中Eijt表示单个劳动力的教育年限；Ejt是在时期t、地区j的劳动力平均教育年限。μijt表示影响人力资本的其他因素；εijt=β′(Eijt-Ejt)+μijt，为个体与地区平均教育水平的差异以及其他影响人力资本因素的叠加。系数β′测量了教育年限增长对劳动力人力资本存量的影响，对应于前文理论模型中的ρ。对(17)式取指数，然后按照地区取平均再取对数得：

(18)

(19)

其中，β″测量了教育的外部性大小，对应于前文理论模型中的ω。联立(16)、(18)、(19)式得：

ln(yjt)=kj+βEjt+θjt

(20)

其中，β=β′+β″，反映了劳动力教育水平提升一年，劳动力的平均收入提升的百分比，即为教育的宏观明瑟收益率。从(20)式可以发现，除了地区间的劳动力教育水平分布差异外，有一个问题可能导致宏观教育收益率的有偏估计：除了在校教育外，还有其他像在职培训、技能学习等因素影响人力资本的积累。如果这些因素跟教育正相关，就可能高估了劳动力教育水平对劳动力平均收入的影响。有两方面原因，本文没有对这些因素进行分析。一方面，像工作经验反映的在职培训，一般用劳动力年龄减去受教育年限和入学年龄得到，因为地区间劳动力的年均入学年龄相似，控制了工作年限和地区固定效应后，会造成多重共线性(20)J. Smith,“Healthy Bodies and Thick Wallets: The Dual Relation between Health and Economic Status”, Journal of Economic Perspectives, 1999,13(2), pp.145-166.。另一方面，通常个体接受的在校教育时间越长，其他学习活动也越多，我们把其他学习活动当成在校教育影响经济产出的中介效应。因此，此估计值包含由在校教育诱导的其他学习活动增加对经济产出的影响。此外，模型中加入省份哑变量，以控制各地区不随时间变化对劳动力人均产出产生影响的因素；以及加入年份哑变量，以控制整体宏观经济波动和变量之间的时间趋势，即采用双固定模型。综上所述，本文所使用的基本宏观明瑟方程为：

ln(yjt)=γ0Ejt+Xjtθ0+Province+Year+μjt

(21)

其中，ln(yjt)为地区j、时期t的劳动力人均收入，Ejt表示劳动力人均受教育年限，Xjt为劳动力人均资本存量对数和劳动力总人口对数等控制变量。Province和Year表示模型中加入的省份和年份哑变量。μjt为随机误差项。则γ0反映了宏观明瑟收益率。

2.估计劳动力的不同层级教育对劳动力人均收入的影响模型

为了捕获劳动力的不同层级教育对劳动力人均收入的影响差异，这里把劳动力的教育水平分为初、中、高三级，来估计以下模型：

ln(yjt)=γ1Midjt+π1Highjt+Xjtθ1+Province+Year+φjt

(22)

其中Midjt表示在地区j、时期t的劳动力人口中，中等教育人口的比例，Highjt表示高等教育人口的比例。模型中没有加入初等教育人口比例变量，因为三者相加等于1，会造成完全共线性。根据以上模型设定，γ1的系数估计值反映了中等教育人口提升百分之一(伴随着初等教育人口比例下降一个百分点)，劳动力人均收入提升的百分比。同理，π1反映了高等教育人口提升百分之一，劳动力人均收入提升的百分比。

(二)变量和数据说明

本研究的样本为中国大陆30个省(市、自治区，剔除西藏自治区)2000—2017年的面板数据。之所以没有选取更久远的数据进行研究，主要考虑到以下两点：其一，在2000年以前，《中国劳动统计年鉴》对劳动力中拥有大专及以上学历占比做了统一统计，没有进一步细分，导致在计算劳动力平均受教育年限时存在较大的测量误差。其二，之前的年份受到计划经济和毕业分配的影响较大，教育的社会回报率得不到完全的反映。各地区劳动力2001年以后的受教育状况的数据来自于《中国劳动统计年鉴》，2000年的数据根据2000年全国人口普查千分之0.95数据进行计算得到。劳动力数量的数据来自于各省份的统计年鉴，用年末从业人员数量衡量；各地区总收入数据来自于《中国统计年鉴》，用地区生产总值衡量。对于物质资本变量，由于目前并没有各省份每年物质资本存量数据的官方统计，本文使用的省际物质资本存量数据根据单豪杰所采用的方法计算得到(21)单豪杰：《中国资本存量K的再估算：1952～2006年》，《数量经济技术经济研究》，2008年第10期。。为了消除通货膨胀的影响，使用GDP平减指数，以1995 年为基期对地区生产总值进行物价调整。

根据以上数据，我们用总收入除以劳动力数量得到劳动力人均收入，总物质资本除以劳动力数量得到劳动力人均资本。把未上过学和不识字转化为0年，小学转化为6年，初中转化为9年，普通高中、中职转化为12年，大学专科转化为15年，大学本科转化为16年，研究生转化为19年，以此来计算各省份劳动力人口的平均受教育年限。初等教育用未上过学和接受小学教育的劳动者占劳动力人口的比重表示，中等教育用接受初中和高中教育的劳动者占劳动力人口的比重表示，高等教育用接受大专及以上教育的劳动者占劳动力人口的比重表示。

沿袭刘智勇等的做法，本文将样本期2000—2017年划分为2000—2002年、2003—2005年、2006—2009年、2011—2013年、2014—2017年五个增长区间进行估计(22)刘智勇、李海峥、胡永远、李陈华：《人力资本结构高级化与经济增长——兼论东中西部地区差距的形成和缩小》，《经济研究》，2018年第3期。。这样处理既可以减轻商业周期波动的影响，又有助于减小序列相关产生的可能性。表1报告了各变量描述性统计的结果。从表中可以发现，平均来看，近些年我国中级人力资本占比最高，其次是初级人力资本。

表1 变量描述性统计

(三)估计结果

1.宏观明瑟收益率的估计结果

表2前两列报告了相关的回归结果，第(1)列是没有控制省份效应的结果，第(2)列是控制了之后的结果。可以看出，在控制了省份效应的影响之后，教育的系数估计值大大降低，说明省份间存在的不可观测异质性差异会高估劳动力教育水平对劳动力人均收入的影响。根据表中第(2)列，教育的宏观明瑟收益率估计值约为5.8%，即劳动力平均受教育年限增加一年，劳动力人均收入约提升5.8 %。此结果既包含教育对人力资本积累的影响，也包含了教育的正外部效应，因此教育对人力资本积累的贡献率要小于此值。参考李锋亮等人、管振和孙志军、孙志军的研究发现教育的人力资本积累效应约为4.0%(23)李锋亮、W. J. Morgan、陈晓宇：《绝对教育年限与相对教育位置的收入效应——对教育生产功能和信号功能的检验》，《中国人口科学》，2008年第1期；管振、孙志军：《教育收益中的人力资本与信号效应估计——基于学制改革的证据》，《劳动经济研究》，2020年第4期；孙志军：《基于双胞胎数据的教育收益率估计》，《经济学(季刊)》，2014年第3期。，结合我们的估计结果可以推断，教育的外部性对劳动力人均收入的提升贡献了约1.8%。

2.不同层级教育对劳动力人均收入影响的回归结果

表2中的最后两列是将教育变量替换为各层级教育变量后的估计结果。与前文的估计结果类似，控制了省份效应后，中等和高等教育的系数估计值变得更小。最后一列的结果说明，劳动力教育的层级越高，对劳动力人均收入和增长率的贡献越大。总的来看，中级人力资本的估计系数要低于高级人力资本的估计系数。说明高级人力资本对经济增长的贡献要大于初级人力资本和中级人力资本，这也与杜育红和赵冉、黄燕萍等的研究结论一致(24)杜育红、赵冉：《教育在经济增长中的作用：要素积累、效率提升抑或资本互补》，《教育研究》，2018年第5期；黄燕萍、刘榆、吴一群、李文溥：《中国地区经济增长差异:基于分级教育的效应》，《经济研究》，2013年第4期。。

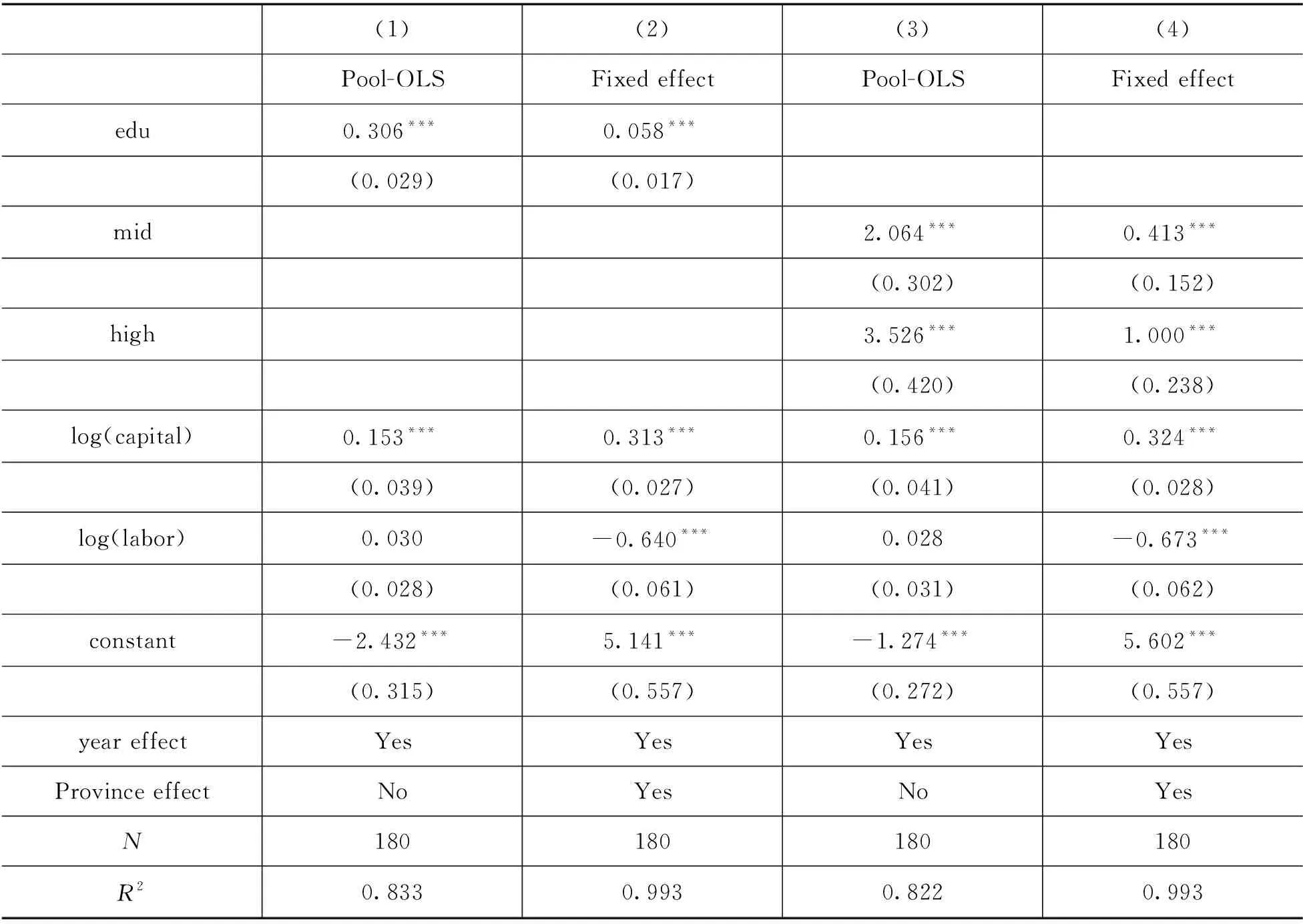
表2 劳动力教育水平对劳动力人均收入影响的回归结果

三、教育水平对人均收入影响的数值模拟

前文主要分析了教育扩张对劳动力人均收入的影响，未涉及到对总人口福利的分析。由于教育扩张降低了劳动参与率，使得教育扩张与总人口人均收入的关系变得更为复杂。在这一节，我们将根据第二节理论推导的结果，结合第三节估计的宏观明瑟收益率和中国的现实参数，分析两者之间的相互关系。

(一)参数校准

2018年中国各地区就业人员平均受教育年限约10.17年，人均GDP约65000元，取基准模型为：E=10，Y/N=6.5。根据世界银行WDI数据库，2010年以来，我国的资本形成率(资本形成总额占国内生产总值的比重)约45%，取储蓄率s=0.45。根据陈昌兵的估计结果，取折旧率δ=0.057(25)陈昌兵：《可变折旧率估计及资本存量测算》，《经济研究》，2014年第12期。。鉴于我国近些年来的人口增长率在5‰左右，取n=0.005。考虑到我国目前的退休年龄为男性60岁，女干部55岁，女工人50岁，取R=57.5。根据国家卫生健康委员会发布的《2018年我国卫生健康事业发展统计公报》，当年中国人均预期寿命约77岁，取T=77。α为资本的产出弹性，发达国家一般为1/3，发展中国家为0.5(26)L. Fanti and L. Gori,“Public Health Spending, Old-age Productivity and Economic Growth: Chaotic Cycles under Perfect Foresight”, Journal of Economic Behavior & Organization, 2011,78(1), pp.137-151；R. A. Pecchenino and P. S. Pollard,“Dependent Children and Aged Parents: Funding Education and Social Security in an Aging Economy”, Journal of Macroeconomics, 2002, 24(2), pp.145-169.。张军利用我国1952 —1998年国家层面的数据估计发现资本的产出弹性约为0.5(27)张军：《资本形成、工业化与经济增长：中国的转轨特征》，《经济研究》，2002年第6期。。综上所述，本文取α=0.5。根据我国义务教育法规定的儿童年满6周岁入读小学，取P=6。参数A0通过数据拟合得到。取A0=0.926，使得基准模型下E=10,Y/N=6.5。各参数的基准取值如表3所示。

表3 参数校准结果

(二)模拟结果

根据以上参数设定，我们将首先考察若教育扩张不挤出劳动参与率，劳动力教育水平与总人口人均收入的关系。然后再分析在此影响中，教育的宏观明瑟收益率、人口增长率和退休年龄的调节作用。为了使结果具有可比性，我们调整A0的值，使得不同条件下，总人口的人均收入初始值在同一水平。

1.基准结果与教育扩张不挤出劳动参与率的结果对比

图3给出了相关的模拟结果。从左图可以发现，如果教育扩张不挤出劳动参与率，则劳动力平均受教育年限与总人口人均收入呈现指数变化关系。此时，教育的边际收益率不变，如右图所示。在考虑到教育扩张对劳动参与率的挤出作用后，劳动力平均受教育年限对总人口人均收入的影响变得更小，而且两者呈现倒U型关系。这是因为教育扩张导致劳动参与率的下降使得教育的边际收益率递减。当劳动力教育水平较低时，劳动参与率下降得较少，教育扩张会增加总人口人均收入。当教育扩张到一定程度后，其带来的人力资本提升作用不足以抵消劳动力数量的减少作用，使得总人口人均收入下降。这样，就存在总人口人均收入达到最大值的点，即教育的边际收益率等于0的点，此点对于理解教育扩张的边界有着重要意义。

从右图可以发现，在基准模型下，教育年限超过31年时，边际收益率才等于0。从这个角度讲，当前我国劳动力的教育水平距离边界点还比较远，实行教育扩张仍然可以提升总人口的人均收入。

2.不同宏观明瑟收益率下劳动力教育水平和总人口人均收入的关系

图4给出了相关的模拟结果。从左图可以发现，宏观明瑟收益率越高，劳动力人均受教育年限的提升对总人口人均收入的影响越大。这是因为在更高的收益率下，随着教育年限的提升，劳动力的生产能力和技术水平提升得更多，导致总人口人均收入增加的也更多。从右图可以发现，宏观明瑟收益率越高，使得边际收益率等于0的点对应的教育年限越大。说明贡献率越大，教育扩张的边界点越远。

3.不同人口增长率下劳动力教育水平和总人口人均收入的关系

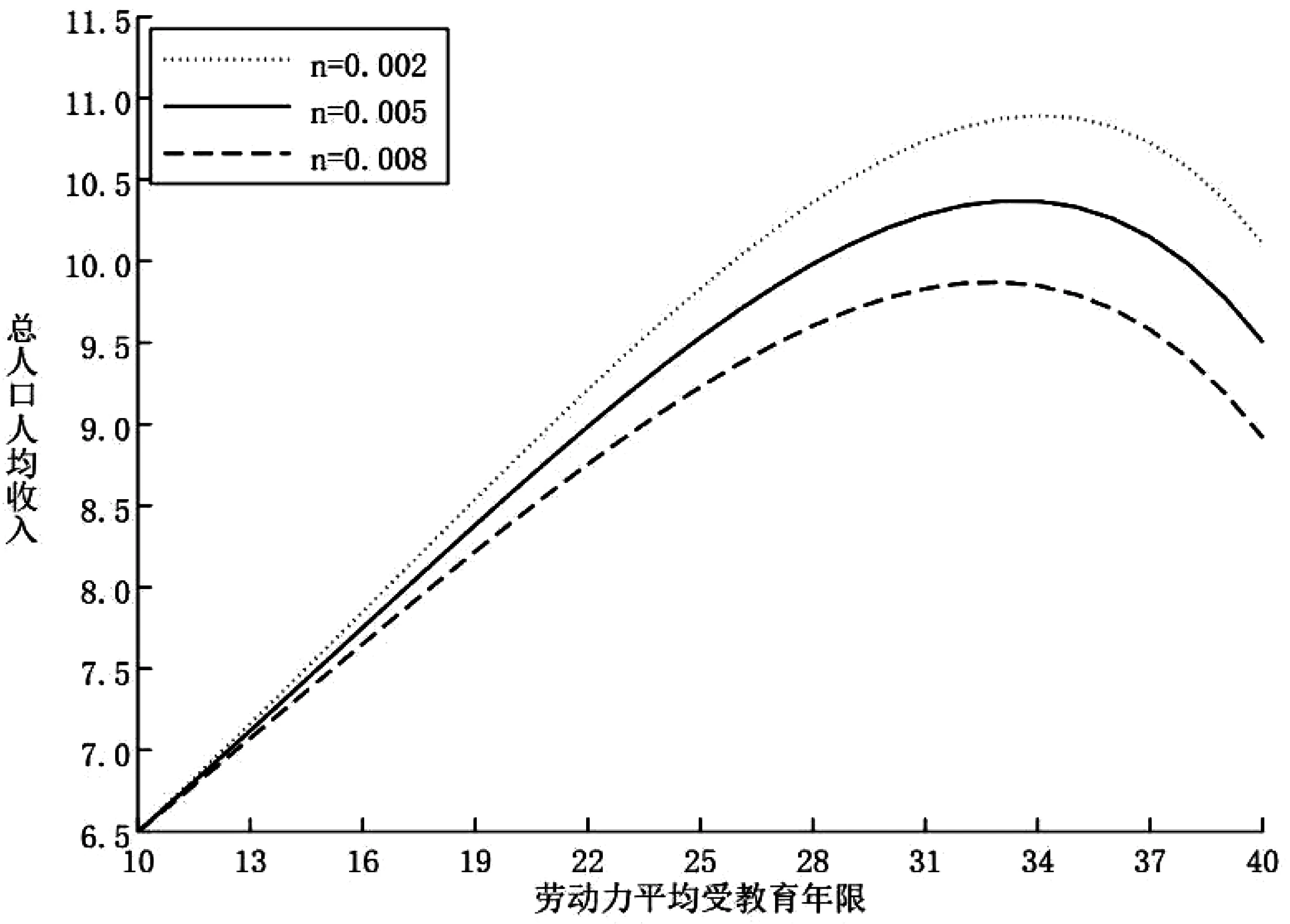
图5给出了相关的模拟结果。可以发现，人口增长率越低，劳动力人均受教育年限的提升对总人口人均收入的影响越大。这是因为人口增长率的提升，降低了劳动力人口占总人口的比例，使得教育扩张对总人口人均收入的影响更小(28)由(9)式可得。。从右图可以发现，人口增长率越低，边际收益率等于0的点对应的教育年限越大。说明人口增长率越低，教育扩张的边界点越远。当前我国人口出生率有着下降的趋势，这不但有利于增加劳动力教育水平对总人口人均收入的影响，也有利于扩大边界点。从这个角度来说，人口出生率的下降，给教育扩张提供了更加有利的条件。

4.不同退休年龄下劳动力教育水平和总人口人均收入的关系

图6给出了相关的模拟结果。可以发现，退休年龄越大，劳动力人均受教育年限的提升对总人口人均收入的影响越大。这是因为退休年龄的增加，增加了个体一生总的工作时间，扩大了劳动力占总人口的比例，使得教育扩张对总人口人均收入的影响更大。从右图可以发现，退休年龄越大，使得边际收益率等于0的点对应的教育年限越大。退休年龄的升高，扩大了教育扩张的边界点。在当前我国人口快速老龄化的背景下，一些学者提出了延迟退休的建议(29)郭凯明、颜色：《延迟退休年龄、代际收入转移与劳动力供给增长》，《经济研究》，2016年第6期；韩克庆：《延迟退休年龄之争——民粹主义与精英主义》，《社会学研究》，2014年第5期。。根据模拟结果，延迟退休政策的实施将有利于增加劳动力人均受教育年限对总人口人均收入的影响，以及扩大教育扩张的边界点。因此，延迟退休将会给教育扩张提供更加有利的条件。

四、结论

与微观研究相比，从宏观上探讨教育的经济价值至少存在两方面的优势。一方面，教育对工资收入的影响中包含了信号效应。从宏观层面进行分析，可以消除这种影响，有利于把握教育的生产功能。另一方面，教育被认为存在着正的外部性，微观层面的研究会低估教育的经济价值。

我们首先把教育的外部性和劳动参与率引入增长方程，从理论上分析了教育扩张对劳动力人均收入及总人口人均收入的影响。分析结果认为，教育扩张尽管可以通过提升劳动力的生产能力和技术进步率促进劳动力人均收入的增长，但是也推迟了劳动力进入劳动力市场的时间，降低了劳动参与率，对总人口人均收入的提升产生一定的阻碍作用。总的来看，教育扩张导致的劳动力教育水平的提升对总人口人均收入呈现倒U型影响。也就是当劳动力的教育水平处在较低水平时，教育扩张可以提升总人口人均收入，但当到达一定程度后，教育扩张反而会降低总人口人均收入。

接下来，我们利用中国大陆30个省份2000—2017年的面板数据，采用宏观明瑟方程，估计了劳动力教育水平对劳动力人均收入的影响。分析结果发现，与理论推导出的结论一致，劳动力教育水平对劳动力人均收入有着正向影响，我国宏观教育收益率约为5.8%。结合一些学者对教育的人力资本贡献率的估计结果，本文认为其中约4%来自于教育对人力资本积累的贡献，1.8%来自于外部性的贡献。此外，与大多数文献的发现一样，我国高级人力资本对经济增长的贡献最大，其次是中级人力资本。

结合理论模型和计量分析结果，利用中国的经济参数进行模拟发现，在当前的经济条件下，教育扩张仍会持续地提升总人口的人均收入。此外，教育的宏观收益率越大，人口增长率越低，退休年龄越大，教育扩张对总人口人均收入带来的正向影响越大，教育的边际收益率等于0的点对应的教育年限也越高。

上述研究结果的政策含义是，我国应该继续实行教育扩张的政策。目前，我国人口红利逐渐消失，经济发展更加依赖劳动力质量的提升。我们研究的结果也显示，在当前的经济条件下，教育扩张不但有利于劳动力人均收入的提升，也有利于全体人口人均收入的提升。此外，在生育率下降、老龄化导致退休年龄延迟概率加大的背景下，教育的经济价值将会进一步显现。

当然本研究还存在一些不足，除了教育数量外，教育质量也对人力资本积累产生重要影响，但是限于数据的可获得性，本文没有对其加以分析。