基于分布式集成方法的区间二型模糊模型设计
李成栋李银萍周长庚
(1.山东建筑大学 信息与电气工程学院,山东 济南250101;2.山东省智能建筑技术重点实验室,山东 济南250101)
0 引言
1965年,ZADEH[1]提出了“模糊集合”的概念,模糊系统理论开始发展。1973年,ZADEH[2]建立了研究模糊控制的基础理论。1974年,MAMDANI[3]将模糊理论应用于锅炉和蒸汽机的控制,此后模糊理论持续发展。模糊系统在建模等领域得到了广泛应用,基于模糊规则的模糊模型具有可解释、可嵌入经验知识等独特的优势。经典模糊模型是基于一型模糊集合的,称之为一型模糊模型。尽管一型模糊模型已经应用于很多领域,但其在处理不确定性时仍有一定的局限性。因此,为了更好地处理这一问题,学者们提出了二型模糊的概念[4-6]。相对于一型模糊集合,二型模糊集合的隶属度由精确值转变为模糊集合,具有更高的自由度,能更好地处理不确定性问题。基于二型模糊集合的二型模糊模型具有更少的规则,但能够获得更佳的性能,已经应用于多个领域。
目前,在该研究领域,已经提出了多种优化方法以实现二型模糊模型的构建。李军等[7]提出了一种基于二型非单值区间二型模糊逻辑系统的多步预测方法,利用反向传播(Back Propagation,BP)算法优化参数,提高了模型的预测精度。陈阳等[8]利用量子粒子群算法优化二型模糊逻辑系统的参数,提高了系统的稳定性。王丹等[9]利用反向传播和最小二乘法分别调整前、后件参数,得到了预测精度较高的二型模糊系统。佃松宜等[10]针对区间二型模糊中规则参数难以设定的问题,提出了改进量子粒子群算法优化模糊集参数,提高了模型的性能。郑高等[11]采用BP算法调整输入以及规则前、后件参数,提高了模型的预测精度。王为国等[12]利用人类学习算法优化模型参数,提高了模型的控制性能。袁顺杰等[13]提出了一种基于自组织特征映射的二型模糊模型,提高了模型的预测精度。赵凤等[14]利用粒子群优化算法对区间二型模糊模型优化,改善了原模型容易陷入局部最优的问题。李军等[15]利用主成分分析与二型模糊系统相结合的方法解决规则“爆炸”问题,并利用反向传播算法和奇异值分解提高计算效率。MELIN等[16]探讨了一种基于遗传算法的神经网络集成模糊响应集结优化结构,可用于时间序列预测。上述已有二型模糊模型训练方法侧重于预测性能的表现,但二型模糊模型输入输出关系较一型模糊模型更为复杂,且具有相对较多的待定参数,从而使得模型计算复杂性上升,模型学习时间变长,在一定程度上影响了二型模糊模型的应用范围。因此,在其设计过程中,除了要考虑系统的性能,二型模糊模型构建过程中的训练时间问题也是不可回避的。
针对上述问题,文章提出了一种基于分布式集成方法的区间二型模糊模型设计策略,采用分布式集成策略得到区间二型模糊模型,并通过最小二乘法优化区间二型模糊模型后件参数,降低模型训练的难度。文章以风力发电和地铁人流量预测为例,通过与自适应模糊系统(Adaptive Network-based Fuzzy Inference System,ANFIS)、反向传播神经网络(Back Propagation Neural Network,BPNN)以及基于差分进化的区间二型模糊模型(Type-2 Fuzzy Model-Differential Evolution,T2FM-DE)对比,验证了该方法的优越性和有效性。
1 模糊集合与二型模糊模型理论概述
1.1 模糊集合
论域X上的一型模糊集A可以由在[0,1]上的隶属度函数μA来刻画,由式(1)表示为

式中μA(x)为x的隶属度,μA(x)∈[0,1]。
论域X上的二型模糊集合A~可由式(2)[17]表示为

式中(x)为x的模糊隶属度函数;Jx为主隶属度;fx(u)为次隶属度。当fx(u)=1时,为区间二型模糊集合。后续提到的二型模糊主要指区间二型模糊。
文章所用到的一型模糊集合为三角形一型模糊集合,如图1(a)所示;采用的二型模糊集合为梯形区间二型模糊集合,如图1(b)所示。区间二型模糊集合的所有主隶属度值并组成的二维区域(图1(b)中的阴影部分)称为不确定覆盖域(Footprint of Uncertainty,FOU),其上、下两条边界分别为上隶属度函数(Upper Membership Function,UMF)和下隶属度函数(Lower Membership Function,LMF)。
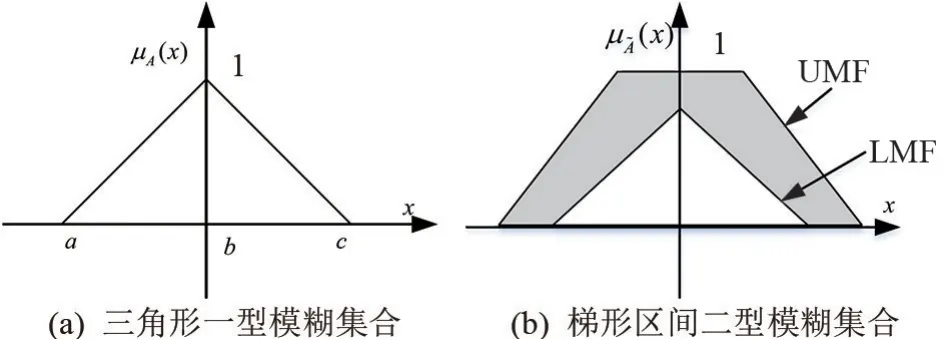
图1 模糊集合图
区间二型模糊集合的隶属度(x)可以由其上隶属度函数和下隶属度函数来刻画,其表达式由式(3)表示为

1.2 二型模糊模型
二型模糊模型的结构如图2所示。其结构与一型模糊模型的结构十分类似,不同之处在于输出处理环节。对于一型模糊模型而言,其输出环节仅有一个解模糊器,但二型模糊模型的输出环节除解模糊器之外还有一个降型器。

图2 二型模糊模型结构图
假定有q个输入变量,对第s个输入变量xs而言,其输入论域可以划分为ms个二型模糊集合,,从而完备规则库共有条模糊规则,其中的第(i1i2…iq)条规则由式(4)表示为
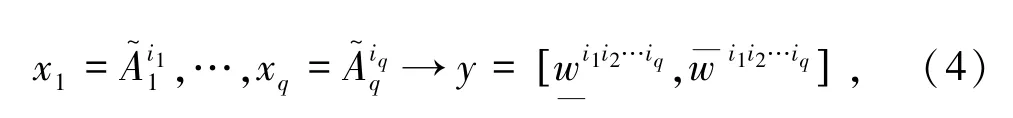
对二型模糊模型,给定输入x=(x1,x2,…,xq)后,通过单点值模糊器和二型模糊推理过程可得到规则(i1i2…iq)的区间激活强度由式(5)表示为

式中和分别为二型模糊集合的下隶属度函数及上隶属度函数。
采用由BIGLARBEGIAN等[18]提出的方法降型及解模糊后得到二型模糊模型的精确输出值y,由式(6)表示为

式中α≥0,β≥0且α+β=1,通常α和β均设定为0.5。
2 基于分布式集成方法的区间二型模糊模型设计
2.1 二型模糊模型整体框架
基于分布式集成方法的区间二型模糊模型设计整体框架如图3所示。

图3 基于分布式集成的区间二型模糊模型构建框架图
该方法的具体实现流程为
(1)将训练数据集X划分为P个训练数据子集,其中P个训练数据子集的大小近似相等;
(2)针对P个训练数据子集,利用ANFIS方法分别构建一型模糊模型,得到P个一型模糊模型;
(3)集成P个一型模糊模型,得到初始区间二型模糊模型;
(4)利用最小二乘法对区间二型模糊模型的参数进行优化,得到最终的模型。
2.2 基于分布式策略的一型模糊模型构建
针对每一个数据子集,训练得到相对应的一型模糊模型。以第p个训练数据子集为例。
(1)确定其第s个输入变量xs的论域范围根据第p个训练数据子集,其上、下界的计算公式分别由式(7)和(8)表示为

(2)对该论域进行一型模糊划分。利用三角形一型模糊集合划分输入变量xs的论域,具体划分结果如图4所示,其中为的中心点。

图4 输入变量xs在第p个模型中的一型模糊划分图
在该一型模糊划分中,输入变量xs的模糊划分数为ms,其第is,p三角形一型模糊集合的隶属函数由式(9)表示为

(3)可以构造出针对第p个数据子集的一型模糊模型的完备模糊规则库,由式(10)表示为
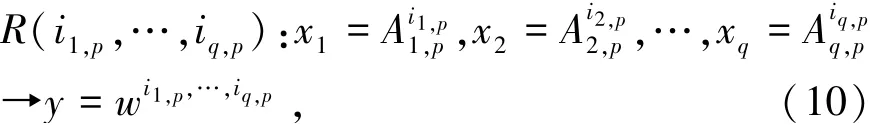
式中q为输入变量个数;is,p=1,2,…,ms;p=1,2,…,P;s=1,2,…,q。规则库共有条模糊规则。
(4)将该模糊规则库中的模糊规则作为初始规则,利用ANFIS方法对这些规则进行优化,从而针对划分的P个训练数据子集构造出相对应的P个一型模糊模型。
2.3 基于集成策略的初始区间二型模糊模型构建
将所得到的P个一型模糊模型进行集成,构造初始区间二型模糊模型。在一型和区间二型模糊模型中都采用完备规则库,为实现集成的目标,只需要将一型模糊划分集成为区间二型模糊划分,将一型模糊规则中的后件集成为相对应的区间二型模糊规则后件。
一型模糊划分的集成主要涉及相对应模糊集合的集成。文章所给出的集成策略如图5所示。在该策略中,提取P个一型模糊模型中的P个三角形一型模糊集合,将P个三角形一型模糊集合进行集成,得到梯形区间二型模糊集合。

图5 一型模糊集合的集成图
从而可以得到初始区间二型模糊模型的规则库由式(11)表示为

式中q为输入变量个数;为规则(i1,…,iq)后件的区间权重,由P个一型模糊模型的规则后件集成得到,其计算式分别由(12)和(13)表示为

2.4 区间二型模糊模型的参数优化
通过分布式集成方法得到了初始的区间二型模糊模型,为进一步强化该模型的性能,需要对其参数进行优化处理。主要考虑区间二型模糊规则后件参数的优化问题,将采用最小二乘方法实现这些参数的学习。
根据式(6),区间二型模糊模型的输入输出关系的向量形式可由式(14)表示为

式中f(x)为模糊规则激活向量;w为区间权重参数向量,分别由式(15)和(16)表示为
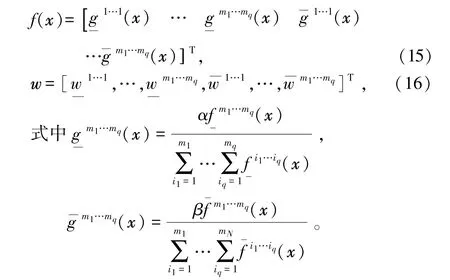

通过训练得到的区间二型模糊规则的区间权重向量w使得预测值和真实值的偏差最小,由式(18)表示为

式中Z为激活度矩阵;y为输出向量,Z和y的计算由式(19)和(20)表示为

该优化问题为最小二乘问题,从而可以得到区间二型模糊规则的区间权重向量w的最小二乘估计,由式(21)表示为
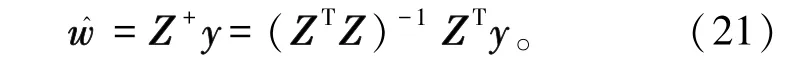
3 区间二型模糊模型在预测问题中的应用
为验证所给出方法的有效性及优势,将其应用于风力发电预测和地铁人流量预测问题中,并与经典一型模糊模型(自适应模糊推理系统ANFIS)、经典神经网络模型(反向传播神经网络BPNN)以及基于差分进化的区间二型模糊模型(T2FM-DE)进行对比。
利用对称平均绝对百分率误差ESMAPE以及均方百分比误差EMSPE来衡量各预测模型的预测精度,其具体计算公式由式(22)和(23)表示为

式中yk为第k个实际数据;为第k个预测数据;K为数据的个数。
同时,为了证明所提模型提高了学习速度,也给出了4个模型的所用训练时间作为对比指标,通过训练时间的长短来说明模型学习速度的快慢。
3.1 风力发电预测
实验所选的风力发电数据来源于公共数据集。所选数据集每隔15 min采集一次风力发电数据,共包含10 000个数据点,选取前8 000个数据进行训练,后2 000个数据进行测试。
实验过程中,划分前8 000个数据,得到数据个数相同的5个训练数据子集,进行一型模糊训练,集成得到初始区间二型模糊模型,利用最小二乘法优化区间二型模糊后件参数。
对比模型的实验参数设置:在ANFIS模型中,迭代次数为100次,每个输入的模糊集个数为3;在BPNN模型中,迭代次数为10 000次;在T2FM-DE中,迭代次数为100次。最后得到的区间二型模糊模型的预测结果如图6所示。实际值与预测值散点图如图7所示,拟合曲线表达式为y=0.9911x+5.4089。
由图6可知,所提模型在风电预测方面效果较好,预测值和实际值的波动曲线相差较小。观察图7中实际值与预测值的散点图可以看出两者的误差较小,说明模型的预测精度较好。
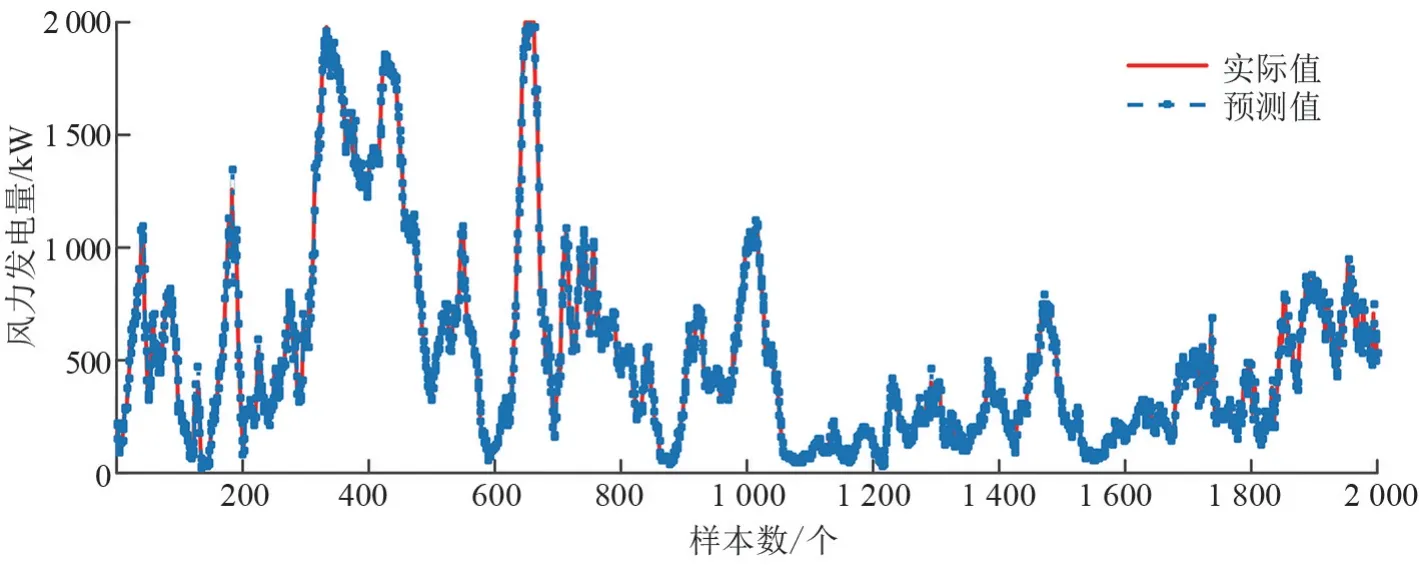
图6 风力发电实验预测结果图
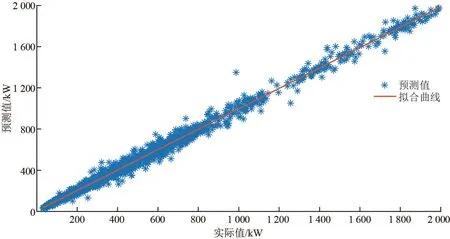
图7 风力发电实际值与预测值散点图
模型性能指标对比结果见表1。

表1 不同预测模型之间的指标对比表
由表1的对比数据来看,在预测精度方面,所提出的区间二型模糊模型的预测精度与ANFIS、BPNN和T2FM-DE模型相近。但在训练时间上,所提模型的训练时间要远小于其他3个模型,比ANFIS、BPNN、T2FM-DE模型分别快约17、40和2 000倍,验证了分布式集成方法的有效性。
3.2 地铁人流量预测
实验所选的地铁人流量数据来源于网站:https://data.buenosaires.gob.ar/dataset? tags=transporte&_tags_limit=0,采集地址为阿根廷首都布宜诺斯艾利斯地铁E号线,伯多Boedo车站。所选数据的采集时间为2018年3月1日至7月31日,采集间隔时间为15 min。所选数据集共包含14 000个数据点,选择前10 000个数据进行训练,后4 000个数据进行测试。
实验过程中,对前10 000个数据进行划分,得到数据个数相同的10个训练数据子集,进行一型模糊训练,集成得到初始区间二型模糊模型,并利用最小二乘法优化区间二型模糊后件参数。
对比模型的实验参数设置:在ANFIS模型中,迭代次数为100次,每个输入的模糊集个数为4;在BPNN模型中,迭代次数为10 000次;在T2FM-DE中,迭代次数为100次。得到的区间二型模糊模型的预测结果如图8所示,实际值与预测值散点图如图9所示,拟合曲线表达式为y=0.9105x+4.8339。模型性能指标对比结果见表2。
由图8可知,区间二型模糊模型在地铁人流量预测中表现良好,且从图9中实际值与预测值的分布可以观察到,除个别数据点外,其他数据误差较小,说明模型的预测精度较好。根据表2可知,所提模型与ANFIS、BPNN以及T2FM-DE模型的预测结果相近。但是,在训练时间上要明显快于其他3个模型,仅需0.9204 s,比ANFIS模型约快68倍,比BPNN模型约快13倍,比T2FM-DE模型约快1 156倍。由此可知,所提方法在保证预测性能的前提下,能够有效地提高了学习速度。

图8 地铁人流量预测结果图

图9 地铁人流量实际值与预测值散点图

表2 不同预测模型之间的指标对比表
4 结论
为加快区间二型模糊模型的训练速度,改善预测效果,文章提出了一种基于分布式集成方法的区间二型模糊模型设计策略。通过实验对比得出以下结论:
(1)建立的模型与ANFIS、BPNN和T2FM-DE等3种模型相比,各模型在风力发电预测实验中测试的ESMAPE和EMSPE分别为3.09%、3.98%、5.48%、3.58%和0.21%、0.26%、0.35%、0.23%;在地铁人流量预测实验中测试的ESMAPE和EMSPE分别为13.03%、19.78%、15.81%、11.14%和1.54%、1.54%、2.83%、0.93%。由此可以看出,所提模型的预测与其他3种的精度相近。
(2)在风力发电和地铁人流量预测中,所提模型、ANFIS、BPNN以及T2FM-DE模型的训练时间分别为0.6708、11.4037、25.7246、1 448.9600 s和0.9204、62.2756、12.1236、1 063.8330 s,所提模型分别比其他3类模型约快17、38、2 160倍和68、13、1 156倍。表明采用分布式并行训练机制及最小二乘法进行参数优化能够显著地加快二型模糊模型的学习速度。

