西南地区地震动特性和参考模型研究

赵兴权邢昊

(1.山东建筑大学 土木工程学院，山东 济南250101；2.西南交通大学 土木工程学院，四川 成都610031)

0 引言

地震是人类所要面临的主要自然灾害之一。我国地震具有频度高、强度大、分布广、灾害重的特点。7度及以上烈度的设防区约占领土面积的51%。1966年邢台地震、1976年唐山地震和2008年汶川地震均造成极大的人员伤亡和经济损失。近年来，随着抗震理论及技术的进步和经济的持续发展，我国抵御地震灾害的能力不断增强，但频繁发生强震所造成的严重灾害风险依旧存在，地震工程领域课题的相关研究仍然显得尤为必要。

正确评估地区的地震动水平是抗震工作的基础，建立地震动模型是最重要的环节之一，许多面临较高地震风险的国家和地区，美国[1-2]、新西兰[3]、智利[4]、日本[5-7]和伊朗[8-9]等均建立了当地的地震动模型。通过数据回归的方法建立地震动模型需要足够多的高质量强震记录，目前我国仅在西南地区具有较多的地震记录，但是这些记录组成的数据库存在地震参数不完备且数据缺失等缺点，难以建立可靠且合理的地震动模型。参考模型法是解决上述问题的可行途径，近年来此方法已在多个地区得到应用[10-12]。参考模型一般是通过已有参数记录海量强震数据库所建立的，即通过借鉴现有参考模型的部分公式形式，利用其他地区的部分强震记录填补目标区域地震记录在某些参数段的空白，以建立目标区域地震动模型。参考模型的评价是此过程的重要一环，直接关系到地震动模型的可靠性。模型评价方法不仅需要利用统计指标评价模型对目标区域地震动的总体预测能力，而且需要分析模型中描述各效应的公式形式与地震动中相应部分的匹配程度。因此，文章提出了一种计算简便、意义明确的模型评价方法，基于我国西南地区的强震记录选择了参考模型，对于今后本地区地震动模型的建立具有较大借鉴意义。

1 地震动参数和地震动模型

1.1 地震动参数

地震动强度采用地震动参数描述。地震动参数是地震引起地面运动的物理参数，主要包括加速度、速度和位移分别对应的时程、峰值和反应谱等。2010年，新西兰坎特伯雷发生了矩震级MW为7.1级的地震，其中一个典型近场(断层最近距离2.0 km的以内)记录的水平向分量(南北向)如图1所示，图1(a)～(c)分别为该台站记录到的加速度、速度和位移时程。目前，强震仪直接记录的是加速度，由于地震发生时仪器产生扭转，因此不能采用传统的积分方式对加速度积分得到相应的速度和位移。图1(b)和(c)展示的速度和位移时程采用类似BOORE[13]的方法积分求解，此近场记录的地面最大加速度为7.3 m/s2、最大速度为1.31 m/s、最大位移为1.6 m，其地面永久位移为1.39 m。

图1 典型近场地震记录时程图

图1虽然展示了3个地震动参数随时间的变化，但无法反映这些地震动参数在频率上的变化。地震动参数随频率的变化一般采用傅里叶谱描述，如图2(a)所示。

傅里叶谱由虚部和实部两个部分组成，计算方法由式(1)表示为

式中Ug(f)为地面加速度时程üg(t)的傅里叶谱，单位与时程中的加速度相同；复数；f为频率，Hz；t为时间，s。傅里叶谱是加速度时程在频域内的一种表达形式，频域反变换到时域由式(2)表示为

一个自振圆频率为ωS、阻尼比为ζ的单自由度结构受到给定地震波激励时，结构位移反应SD(ωS，ζ)可由式(3)～(5)表示为

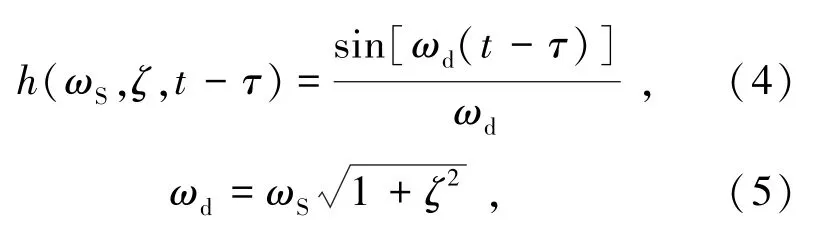
式中Tpeak为单自由度结构达到反应最大值的时间(时间超过Tpeak后的地震波所含能量对结构的最大反应无影响)，s；h(ωS，ζ，t)为结构位移脉冲函数；SD为位移反应谱(结构相对于地平面的最大位移)。

结构的最大相对速度和最大加速度可将相对速度和加速度脉冲代入式(3)得到。在阻尼比(约为5%)和周期(＜5.0 s)均较小时，伪速度谱SPV和伪加速度谱SPA的计算公式分别由式(6)和(7)表示为

傅里叶谱的模描述地震动在频率的分布状态。地面加速度时程的傅里叶谱如图2(a)所示，地震波的能量在不同周期的分布呈现较大的随机性，但傅里叶谱在周期的分布也可以找出规律并通过理论参数描述。图1(a)加速度时程的反应谱如图2(b)所示，可以看到傅里叶谱与反应谱几乎无相似之处。在周期为0.5 s时，加速度反应谱为14.64 m/s2，由式(7)计算的位移谱为0.09 m。虽然这些参数与结构的实际变形参数未必相等，但可为设计人员提供直观的结构设计信息。对于一个弹性结构，其地震反应可以分解成一系列振型，每个振型都可用一个单自由度结构的反应进行描述，每一个单自由度结构具有该振型的自振频率和阻尼比，各个单自由度的结构反应进行有规律的叠加，即可得到结构在该地震波作用下的精确反应。对于大部分结构，其第一振型反应往往远远大于其他振型甚至之和，经过归一化的第一振型的结构反应即可表征一个结构的主要地震反应，以此可以较为精确地估算结构的地震反应，也可根据归一化原则估算出高阶振型对地震反应的影响。地震动模型计算得到的地震动参数通常表示结构第一振型的动力反应。

图2 典型近场地震记录加速度时程的傅里叶谱和反应谱图

阻尼比是准确计算结构的地震反应的另一重要结构参数。钢结构的阻尼比一般较小，通常为1%～4%。索式结构自身阻尼比非常小，约为1%，钢筋混凝土结构处于弹性反应阶段时的阻尼比约为3%～5%。另外，建筑结构的阻尼比同时会受到振动幅度的影响，如在背景噪音时结构震动所显示的阻尼比要远小于在地震作用下结构显示的阻尼比，原因在于地震作用下结构和非结构构件之间产生的相对位移耗散了能量，提高了结构反应时的阻尼比。综合这些特性，地震设计反应谱的阻尼比一般选为5%。简化的计算结构地震反应过程如图3所示。

图3 四自由度结构计算地震反应示意图

一个结构的弹性反应可按振型分解，对于绝大多数结构，总体结构反应主要来自第一振型反应，相应的地震反应谱表征结构反应的位移、速度和加速度，是结构抗震设计的重要参数。

1.2 地震动模型

场地的设计反应谱一般通过分析概率地震危险性分析得到。大致过程是:通过地质调查和收集历史地震等信息确定研究地区出现超过某一震级地震的概率，再根据地震动模型计算给定震级、地震深度、震源机制、地震距离和场地条件等情况下该场地的反应谱。此过程的地震动模型通常也称地震动衰减关系。地震动模型的建立通常有3种基本方法，即(1)根据一定数量的目标地区的地震观测数据计算回归[14-15]；(2)利用目标地区和参考地区之间的差异调整参考模型[16-18]；(3)获取回归利用随机振动模型计算的地震动[19-20]。目前，通过数学模型回归实测地震数据的方法(1)被公认为最准确的方法。由于地震震源破裂过程、地震波的传播路径和场地条件极为复杂，而地震动模型又只能选择相对简单又容易得到的参数，因而每个模型都有相应的残差标准差。在进行概率地震危险性分析时，这些残差标准差也是重要的参数。

长期以来，我国缺少足够数量的强震记录，无法利用方法(1)得到地震动模型，只能借助地震烈度数据间接推导[21-23]。2007年我国数字强震动观测台网开始运行，数年来在地震多发的西南地区获得了大量强震记录，包括汶川地震(MW7.9)、芦山地震(MW6.6)和康定地震(MW6.2)。卢大伟等[24]、喻畑等[25]、姜倩等[26]和党鹏飞等[27]均利用这些强震记录建立了地震动模型。

2 强震数据库

收集了截至2014年12月初的我国西南地区的强震记录，经过滤波及波形检查，排除了研究区域之外的记录，并采用ZHAO等[5]的震级-距离截断方法排除了震级小而距离远的记录，最终的强震数据库包括2 403条强震记录，来自449个地震事件，由390个台站记录得到。地震动模型一般采用矩震级，数据库中少部分地震的矩震级来自一些地震研究机构发布的目录，其余利用兰晓雯[28]提出的公式由面波震级转化得到。台站场地条件的确定，对于有钻孔波速数据的部分台站可以直接得到，其余则通过ZHAO等[29]提出的H/V(水平向地震动和竖向地震动反应谱之比)方法确定，场地类别(Site Class，SC)的划分遵循ZHAO等[5]的方法，将场地分为场地周期＜0.2 s为SCⅠ、0.2 s≤场地周期＜0.4 s为SCⅡ、0.4 s≤场地周期＜0.6 s为SCⅢ、场地周期≥0.6 s为SCⅣ等4类。地震的断层类型根据BOORE等[30]的方法确定，分为正断层(N)、正斜断层(NO)、逆断层(R)、逆斜断层(RO)、走滑断层(SS)以及断层信息未知(UD)等6类。距离参数采用断层最近距离或震源距离，深度参数采用断层深度或震源深度。不同断层类型的地震关于震级和地震深度的分布如图4(a)所示，不同类别场地的记录关于震级和距离的分布如图4(b)所示，不同场地类别和断层类型记录的数量分布见表1。由此可知，数据库在6.3至7.8级的震级区间仅有一个地震，且大部分地震没有明确的断层类型，同时强震记录在不同场地类别的分布也不均衡，难以利用我国西南地区强震记录独立建立可靠且合理的地震动模型。

图4 地震事件和记录关于主要地震参数的分布图

表1 不同断层类型和场地类别的强震记录的数量表

3 参考模型的选择

3.1 水平分量模型评价方法

为选择参考模型，设计一个计算简单、意义明确的模型评价方法。计算我国西南地区实测地震动的反应谱与备选模型的预测反应谱之间的总残差，由式(8)表示为

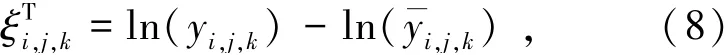
式中yi，j，k为第i个地震事件的第j个记录的地震动反应谱，由第k个台站获得；为对应的模型预测值；为总残差。

采用随机效应方法将总残差继续分解，由式(9)和(10)表示为

式中c为常数校正项；ηi为地震i的震间残差，服从均值为0，标准差为τ的正态分布；εi，j，k为震内残差，服从均值为0，标准差为σ的正态分布；θk为场地k的场地间残差，服从均值为0，标准差为τS的正态分布；ξi，j，k为场地内残差，服从均值为0，标准差为σS的正态分布。震间标准差σ的计算方法由式(11)表示为

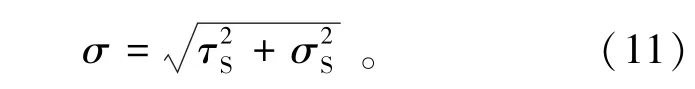
如果分解总残差的式(9)中不包括常数校正项c，那么震间标准差τc由式(12)表示为

式中为式(9)中c的估计值；n为地震事件数量。

若式(9)不使用常数校正项c，对数最大似然值(Maximum Log-likelihood，MLL)会降低，但如果强震数据库中数据总量大且数据分布均匀，即使当ĉ很大的情况下，场地间标准差τS也不会显著增大，这意味着常数校正项c可以作为评估模型预测值相对于实际地震动偏移程度的参数，而不仅是在式(9)中作为震间残差的一部分。常数校正项c、震间标准差τ、场地间标准差τS和场地内标准差σS可以评估模型对数据拟合的优劣，是模型评价方法中的第一类评价指标。最佳模型应具有最接近0的常数校正项c和最小的标准差，且不经修改就可应用于目标区域。

模型中描述各类效应的数学表达式和地震动中相应部分的匹配情况是评价模型优劣的重要参照。一系列基于物理概念的校正公式量化了各类效应在模型与实际地震动之间的不匹配程度，如果某个模型的校正项系数的绝对值最小，就可认为该模型对这项地震动效应的拟合效果相对较好。校正震间残差相对于断层类型和震级偏移可由式(13)表示为

式中a1为常数，a2、a3和a4分别为3类断层类型修正项的系数；下标N、R和SS分别表示正断层或正斜断层、逆断层或逆斜断层以及走滑断层，这3类断层修正项是相对于断层信息未知(UD)的地震设置的。对正断层(N)和正斜断层(NO)的校正项系数非常相似，故将两类断层合并，对逆断层(R)和逆斜断层(RO)亦如此。虚拟变量δN在正断层或正斜断层时为1.0，其他断层类型时为0.0。虚拟变量δR在逆断层或逆斜断层时为1.0，其他断层类型时为0.0。虚拟变量δSS在走滑断层时为1.0，其他断层类型时为0.0。b1、b2和b3为震级校正项的系数，mi为第i个地震事件的震级，震级常量msc和mc分别为6.3和7.1。mc＝7.1时，数据库中震级空档的影响有所降低，原因在于震级＜7.1的震级标度比率可以由3.5至6.6级地震外推得到，震级＞7.1的震级项系数受到连续性的震级公式和汶川地震数据制约，即地震动模型计算的反应谱不能与汶川数据完全相符，但需要在给定概率下，尽可能与汶川数据保持良好的拟合效果。

校正震间残差相对于深度偏移可由式(14)表示为

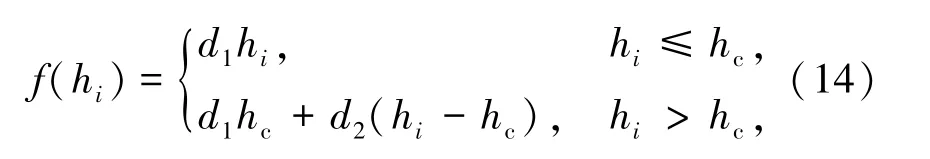
式中d1和d2为深度校正项系数；hi为第i个地震事件的断层深度或震源深度；hc为深度常数。

式(13)和(14)中的校正项系数通过固定效应模型进行计算，由式(15)表示为

式中ηi为式(9)分解得到的震间残差；γi为剩余震间残差，服从均值为0，标准差为τN的正态分布。

校正震内残差相对于距离和场地参数偏移可由式(16)表示为

式中ξi，j，k为式(9)分解的震内残差；e1、e2、e3、e4分别为常数项、场地校正项系数、非弹性衰减校正项系数和几何衰减项校正系数；TVS30k为第k个场地的场地周期，由120/VS30计算；xi，j，k是由第k个场地记录到的第i地震的第j个地震动的距离；xcro是避免震级饱和而设置的距离常数，防止距离为0时预测反应谱随震级增加而减小；c1c、c2c和mc分别为ZHAO等[6-7]的模型系数；ψk为剩余场地间残差，服从均值为0，标准差为τNS的正态分布；λi，j，k为剩余场地内残差，服从均值为0，标准差为σNS的正态分布。

各类校正项的系数构成了模型评价方法的第二类评价指标，校正项系数越接近0，模型中效应项与实际地震动中相应部分就越匹配。剩余标准差是第三类评价指标，在第三类评价指标上评价效果最理想的模型是经修改后应用于目标区域的最佳模型。

3.2 水平分量参考模型的选择

选择ABRAHAMSON等[1，31]、CHIOU等[2，32]和ZHAO等[7]中的模型作为备选模型，分别简称AS2008模型、ASK2014模型、CY2008模型、CY2014模型和Z2016模型。ANDERSON等[33]的研究表明正值的正断层项系数可能仅对发生在日本的地震有效，故将Z2016中正值的正断层项系数设置为0，此模型称为Z2016N模型。之后的分析发现，在大多数指标上，Z2016N模型对我国西南地区地震动的拟合均优于Z2016，因此在备选模型间的比较中，只展示Z2016N的结果。5个模型的对数最大似然值MLL的相对值如图5所示，即每个模型的MLL减去Z2016模型的MLL值，横坐标为从峰值地面运动加速度(Peak Ground-Motion Acceleration，PGA)至5.0 s的谱周期。当某个模型的MLL相对值为正时，表明该模型优于Z2016模型；当相对值为负时，则表示该模型在统计上劣于Z2016模型。结果显示，除了Z2016N模型的MLL相对值在有些谱周期上为正，其他所有模型的MLL相对值均为负，即劣于Z2016N模型。Z2016N模型的常数校正项c的绝对值在很多周期上小于其他模型，如图6所示。各个模型的震间和震内标准差如图7所示。对于这两项标准差(特别是震间标准差)，Z2016N模型的值均小于其他模型，表明Z2016N模型比其他模型更适用于我国西南地区的地震数据。

图5 各水平分量模型的MLL相对值图

图6 各水平分量模型的常数修正项c图

图7 各水平分量模型震间标准差和震内标准差图

为了对每个模型的参数进行综合判断，利用常数校正系数c、震间标准差τ、场地间标准差τS和场地内标准差σS这些评价指标，以0.5 s为界分为两个周期区间进行平均，在某个指标上评价效果最理想的模型得分记为5，反之则为1。如果两个模型某个指标较为接近(相差在5%之内)，那么两个模型在此指标的得分取均值。各备选模型在第一类评价指标上的得分见表2，最后一列为平均得分，发现Z2016N模型的得分最高，是可直接应用于我国西南地区的最佳地震动模型。各备选模型在第二类评价指标见表3和4，即校正系数绝对值排列得分，表明Z2016N模型和AS2008模型中的各类效应项与我国西南地区地震动中相应部分最匹配。各备选模型在第三类评价指标上的得分见表5，表明Z2016N模型是经修改后应用于我国西南地区的最佳模型。

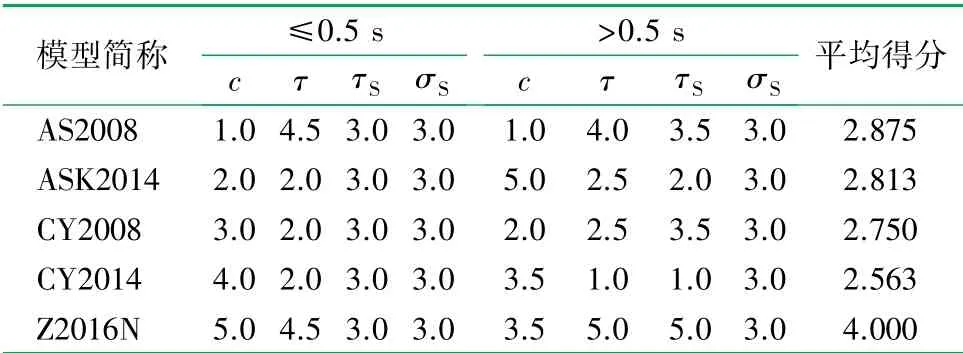
表2 各模型对我国西南地区水平向地震动整体拟合优劣得分表

表3 各模型校正系数得分汇总表(≤0.5 s)

表5 校正后模型对我国西南地区水平向地震动整体拟合优劣得分表

表4 各模型校正系数得分汇总(＞0.5 s)及全周期平均得分表

3.3 竖向分量模型评价方法和参考模型选择

数据库中竖向分量对应的地震和记录数量与水平分量模型基本相同。作为备选的5个竖向地震动模型分别来自BOZORGNIA等[34]、ÇAGˇNAN等[35]、GÜLERCE等[36]、STEWART等[37]和ZHAO等[38]，简称为BC2016模型、CAKS2017模型、GKAS2017模型、SBSA2016模型和Z2017模型。BC2016模型、GKAS2017模型和SBSA2016模型是NGA-WEST2项目的一部分，分别是基于CAMPBELL等[39]、ABRAHAMSON等[1]和BOORE等[40]的模型形式建立的。CAKS2017模型组合了由欧洲和中东地震记录建立的水平向地震动模型[41]和H/V模型[42]。Z2017模型是基于日本俯冲带地区的浅壳和上地幔地震记录建立的。CAKS2017模型采用RJB(从台站到断层地表投影的最近距离)作为距离参数，其他4个模型采用断层最近距离。BC2016模型排除了余震记录，GKAS2017模型的数据库中包含余震记录且在模型中设置了余震项，CAKS2017模型、SBSA2016模型和Z2017模型使用了余震记录，但模型中没有余震项。5个模型中只有SBSA2016模型考虑了场地非线性。与水平分量模型Z2016模型相似，Z2017模型也具有正值的正断层项系数，仍将其设置为0，即采用Z2017N模型取代Z2017模型进行对比。BC2016模型、GKAS2017模型和SBSA2016模型使用了我国西南地区记录用于计算的小部分非弹性衰减调整项，Z2017N模型利用汶川地震的记录计算大震级项，CAKS2017模型没有应用我国的地震记录。

与分析水平分量相同，采用式(8)和(9)进行残差分解并计算cV，其中下标V代表竖向分量。各模型的MLL相对值如图8所示，Z2017模型的MLL在0.2 s之前比Z2017N模型略小，在0.2 s之后与Z2017N模型相当。BC2016模型、CAKS2017模型、GKAS2017模型和SBSA2016模型的MLL均比Z2017N模型小得多。5个模型的常数校正项cV对比如图9所示，在大多周期上，Z2017N模型的常数校正项cV的绝对值均小于其他模型。BC2016模型、GKAS2017模型和SBSA2016模型在所有周期都低估了我国西南地区的竖向地震动，CAKS2017模型和Z2017N模型在0.5 s之前和2.0 s之后也低估了我国西南地区的竖向地震动。CAKS2017模型的cV在0.3 s之前最大，Z2017N模型的在0.45 s之前最小。GKAS2017模型和SBSA2016模型的cV在大部分周期都非常接近，BC2016模型的cV在1.5 s之后最大。整体来看，Z2017N模型与我国西南地区的竖向地震动更为接近。

图8 各竖向分量模型的MLL相对值图

图9 各竖向分量模型的常数校正项c V图

5个竖向模型的震间标准差τV和震内标准差σV如图10所示。Z2017N模型的τV在除0.04和0.05 s之外的其他周期均最小且在0.4～0.6之间变化。CAKS2017模型的τV在0.1 s之前与Z2017N模型非常接近，BC2016模型、CAKS2017模型和GKAS2017模型的τV随周期的变化曲线近乎平行(差值在不同周期上几乎相同)，BC2016模型和GKAS201模型的τV相差不多，而CAKS2017模型的τV比BC2016模型和GKAS2017模型的平均约小0.15。1.0 s之前，SBSA2016模型的τV与BC2016模型和GKAS2017模型非常接近；而在1.0 s之后，SBSA2016模型的τV比其他两个NGA模型的更小。最大的τV是BC2016模型在4.0 s的1.069，而最小的是Z2017N模型在0.2 s的0.414。5个模型的σV随周期的变化曲线相似，Z2017N模型的σV在大部分周期都最小，但在数值上和其他4个模型相差不大；0.6 s之前，CAKS2017模型的σV最大；0.6 s之后，BC2016模型和GKAS2017模型的σV最大。

图10 各竖向模型的震间标准差和震内标准差图

各模型的场地间标准差τV，S和场地内标准差σV，S如图11所示。5个模型的τV，S在0.15 s之前相差较小，CAKS2017模型的τV，S在这一周期区间最小。0.15 s之后，Z2017N模型的τV，S最小。整个周期内，最大的τV，S是BC2016模型在1.5 s的0.597，最小的是Z2017N模型在5.0 s的0.2。GKAS2017模型和Z2017N模型的σV，S在0.3 s之前最小，CAKS2017模型的σV，S在这一周期区间最大。0.3 s之后，5个模型的σV，S相差较小。在所有周期内，最大的σV，S是CAKS2017模型在0.2 s的0.551，最小的是SBSA2016模型在3.0 s的0.406。

图11 各竖向模型的场地间标准差和场地内标准差图

对于竖向分量，建立了与式(13)～(17)相同的模型校正方程，计算了校正系数和校正后的剩余标准差。各竖向模型在第三类评价指标上的得分见表6，表明Z2017N模型比其他4个模型均更适于作为我国西南地区竖向模型的参考模型。

表6 校正后模型对我国西南地区竖向地震动整体拟合优劣得分表

4 结论

西南地区是我国地震风险最高的地区之一，地震动模型对这一地区的抗震工作非常重要。参考模型法是建立我国西南地区地震动模型的可行方法，模型的选择和评价是这一方法的关键环节。采用一种基于实际地震动的模型评价方法，评估了来自美国、日本等的5个水平向地震动模型、5个竖向地震动模型在我国西南地区的适用性，主要得出以下结论:

(1)基于日本浅壳和上地幔记录的Z2016N模型对我国西南地区水平向地震动的模拟效果最好，是可以直接应用于我国西南地区的最佳模型。

(2)Z2016N模型中各地震效应项与我国西南地区水平向地震动中相应部分拟合效果最好，校正后模型的标准差也最小，可作为应用于我国西南地区的最佳参考模型；基于日本浅壳和上地幔记录的竖向地震动模型Z2017N是适用于我国西南地区的最佳竖向模型和最佳竖向参考模型。