基准偏移在尺寸链公差累加计算中的作用及计算结果六西格玛意义的实践
黄恭勤,田立群
(安波福电子(苏州)有限公司, 江苏 苏州 215126)
0 引言
机械工程师在设计与研发工程中,需要为关键特征设定公差范围;然而这些公差是否可以满足功能要求,就需要进行尺寸链公差累加计算分析。当尺寸特征控制框中包含基准偏移的时候,如何带入这些偏移的影响,以及如何评估计算分析结果的六西格玛的意义,就会成为工程师需要面对的问题。
1 饰件组装及其图样案例
1.1 案例介绍
如图1所示,3个衬板(衬板1、衬板2和衬板3)装配在面板上。现在需要探究衬板3和面板之间上部的间隙大小。

图1 面板和3个衬板的组装
图2所示为面板标注图,由于衬板3和衬板2,以及衬板2和衬板1之间的间隙也需要探究,所以衬板3在面板上的定位孔以衬板2在面板上的定位孔为基准被控制位置度;衬板2在面板上的定位孔以衬板1在面板上的定位孔为基准被控制位置度;从制造工艺的角度出发,面板上侧轮廓度以下侧孔B和腰槽C为基准控制[1]。由于面板使用多个固定尺寸功能检具(fixed-size functional gage)检测关键尺寸和公差,特征控制基准普遍使用了基准偏移(标注表现为基准后面有@MMB标记)。
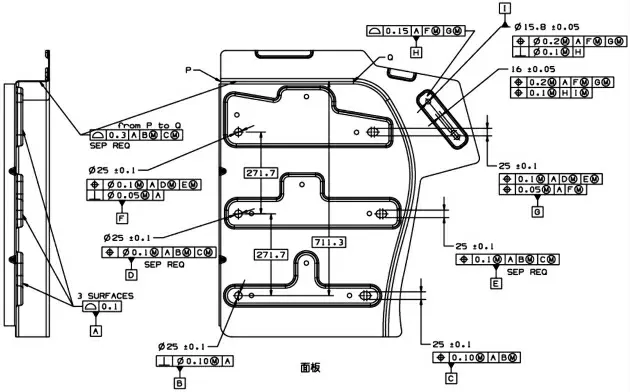
图2 面板公差标注图
图3所示为衬板3标注图。类似于面板,轮廓度的控制也使用了基准偏移(标注表现为基准后面有@MMB标记)。

图3 衬板3的公差标注图
1.2 初步尺寸链公差累加计算
为了探究图1 中间隙的大小,进行了初步的尺寸链公差累加计算,结果为: Max(最大值)=2.9,Min(最小值)=1.8。然而在所有部件被检测合格的情况下,部件装配后间隙有时却在1.8~3.0范围之外。这是部件检测的过程出现了问题,还是尺寸链公差累加计算出现了错误?后经研究发现,所有部件检测的过程中都正确地使用了固定尺寸功能检具进行了可靠的检测;然而,在初步的计算中却忽略了所有的基准偏移在公差累加计算中的作用(即所有的图样中基准符号后面的@MMB都被忽略了)。这样产生如下的问题:在这个案例中,基准偏移在公差累加计算中的作用到底有多大?其作用或者影响是否可以被忽略?
2 使用双列累加计算方法重新进行尺寸链公差累加计算
为了解决上面的问题,使用双列累加计算方法(Two Column Stack Method)对这个案例进行了重新的计算。累加计算尺寸链如图4所示。计算间隙为衬板3和面板间的间隙。因为3个衬板在装配的时候都需要另外安装其它的有相当质量的部件,所以尺寸链考虑了重力的作用;在此前提下,这个尺寸链图可以同时计算出间隙的最大值和最小值。
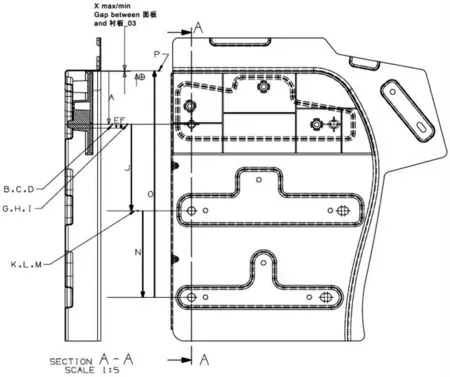
图4 尺寸链图
双列累加计算方法(Two Column Stack Method)计算过程如图5所示。
双列累加计算方法主要特点为:不同于使用外部边界(OB)和内部边界(IB)追究单个特征对象极限边界进而展开计算的比较具有一般性的方法,位置度和轮廓度的值被细分。例如位置度的值被细分为3项:1)特征控制框内数值;2)位置度补偿值(Bonus);3)位置度基准偏移值(Datum Shift)。例如图5中G、H、I行和K、L、M行。
因为值被细分,各个量就可以被细致地追究。例如图5中G,H,I行:
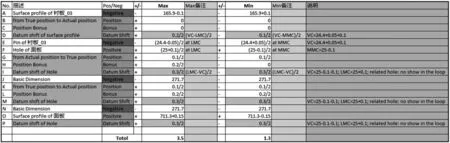
图5 双列累加计算方法过程图
1)行G取决于对应孔的位置度数值0.1,0.1/2被填入最大值列及最小值列(在这里,因为尺寸链向量经过的是孔半径,所以表格数值取用0.1/2);
2)行H的取值相关于行F对应孔的取值,因为行F最大值列取值(25+0.1)/2为最小材料状态,所以行H最大值列的取值为0.2/2(即(LMC-MMC)/2),而行F最小值列孔取值为孔最大尺寸状态(MMC),所以行H最小值列取值为0(MMC没有Bonus);
3)行I录入的数值为对应孔的基准偏移量,而这个基准为基准D及基准E对应的孔和腰孔。在尺寸链中这个孔及腰孔对应的尺寸大小并没有出现,那么无论对于求解间隙的最大值还是最小值,这行的偏移量都应该录入偏移量的最大值[2]。故对于基准D及基准E对应的孔和腰孔:VC=25-0.1-0.1;LMC=25+0.1(VC为Virtual Condition,即实效状况);Datum shift=(LMC-VC)/2=0.3/2=0.15。
面板诸多特征孔垂直度的意义被包含在对应的其他尺寸或者位置度或轮廓度中,它们(垂直度等)对于此尺寸链公差累积计算过程不产生影响。
对于行H,如果对于求解最大值和最小值,都填入了0.2或者0,皆是在计算中带入了一个错误:额外带入一个不存在的量或者遗漏一个量;对于行I,对应孔或者腰孔的尺寸并没有出现,追究相应孔的外部边界及内部边界的算法就不再适用。从本案例可以看出,双列累加计算方法(Two Column Stack Method),对于位置度和轮廓度控制拥有补偿量(Bonus)和基准偏移量(Datum Shift)的案例非常适用,分析过程紧随GD&T的固定尺寸功能检具意义,解算过程清晰明了;分析结果明确可信,无争议。当然这个方法也有它本身的缺点,即计算过程相对复杂,使用Excel等工具实现求解逻辑的过程相对困难,对分析操作者对于GD&T及固定尺寸功能检具意义的理解程度提出了更高的要求。
按照这个方法,最后解算的结果为:最大值为3.5,最小值为1.3。这个结果和初步累加计算的结果(Max=2.9,Min=1.8)比较,差别明显很大;很显然,如果这个差别被忽略,进而产生的工程风险是相当大的。
3 双列累加计算方法结果六西格玛意义的实践
上述双列累加计算方法产生的结果,体现了极端的情形(Worst case situation)的分析意义。也就是对于本案例,当各个部件都通过检测的情况下,部件组装后的被分析的间隙是不会超出计算结果(最大值为3.5,最小值为1.3)的。这个结果关注的是工程风险最低的安全性,然而却忽视了风险概率的意义。也就是从六西格玛的立场来讲,一般情况下,工程师根据统计学的实践意义会关注六西格玛理论下的极值(最大值和最小值)。
上述陈述对应的实际情况为:当个别部件有少量超差的时候,我们会希望得出基于六西格玛的极值,继而判断这个少量超差会使结果突破目标要求,还是概率意义上风险可控。
一般来讲,在考虑六西格玛意义的时候,根据经验,经常是将各个公差取平方后求和,然后开平方根,再乘以一个修正系数(一般为1.5),进而获得最大值和最小值。然而这个方法在面对上面的计算过程时,会变得繁琐,并且根据经验很容易降低结果可靠性。这时候,是否有一个更为简明和可靠的方法可以实现六西格玛的实践意义?
如图6所示,在六西格玛质量水平的要求下(考虑了正态分布1.5倍标准差的偏移),总缺陷概率为3.4×10-6而上述案例结果(最大值为3.5,最小值为1.3)为不考虑概率意义的分析结果,它的缺陷概率理论上为0;0缺陷的意义在统计学的理论来讲即为7西格玛的水平[3]。所以我们可以直接将上述结果定义为7西格玛的结果。根据这个理论解读,可以计算标准差的大小:标准差=(Max-Min)/14=(3.5-1.3)/14=0.157。
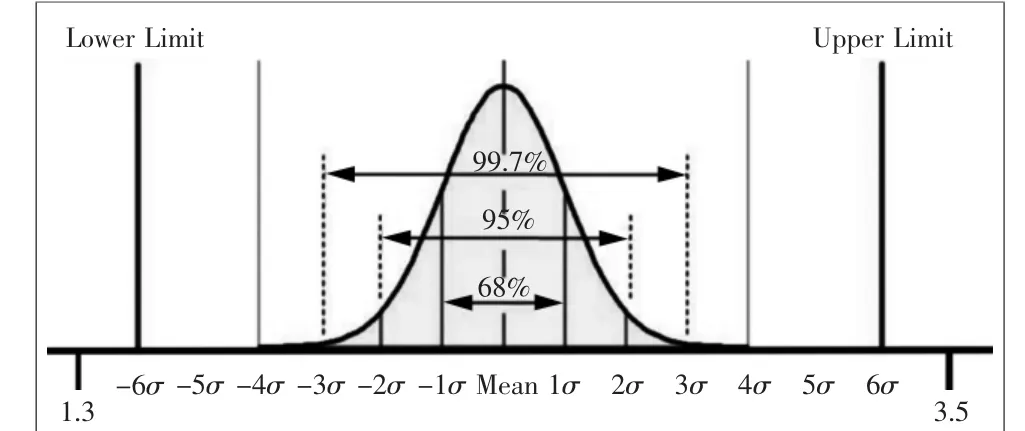
图6 双列累加计算方法结果六西格玛意义
这样,如果目标西格玛水平被定位在5西格玛的话,上面分析结果即为:最大值=3.2,最小值=1.6(Max=3.2,Min=1.6)。这样,大概单边0.3双边0.6的公差范围被研发人员获得。在当前竞争严酷、品质追究严厉的行业背景下,上面的公差范围是非常珍贵或者具有决定性的。
4 基准偏移在尺寸链公差累加计算中的作用及计算结果六西格玛意义的实践总结
在不同行业或者情况下,尺寸链公差累加计算具体操作方式和方法是不尽相同的。对于相对规整、部件形状和部件间组装关系基本表现在正交关系的时候,可以借助Excel表格或者类似的二次开发工具展开累加计算;对于部件形状复杂、基准特征及部件间关系为空间自由形状(即不再是正交关系)的案例,借助基于3D CAD环境的专业TSU软件可能会是必要的选择。对于本文出现的案例,部件间基准和被控制特征基本属于正交关系,同时基准偏移的影响对于结果的影响达到了不可以被忽略的程度,这时候本文提供的双列累加计算方法(Two Column Stack Method)无疑可以作为这样情况下最佳的公差累加计算解决方案。
对于各种公差累加计算结果六西格玛意义的实践,不同算法条件下的表现形式经常是有所不同的。基于上文阐述的双列累加计算方法所具有的细化无争议的特点及六西格玛的理论意义,本文提出的求解标准差的方法简明、易于操作,有利于工程师在实践工作中争取产品成本下降空间,有助于使研发过程确保立于不败之地。

