中型无人直升机电动舵机控制器设计与实现
李晨毓,祖家奎,刘佳晖,高尚文
(南京航空航天大学自动化学院,江苏 南京 211106)
0 引言
当前,无人直升机作为无人机家族的重要成员之一,具有的独特飞行能力和应用价值,使其成为广泛研究的对象[1]。无人直升机独特的飞行性能与其独特的操作机构密不可分,对于常规单旋翼带尾桨的直升机而言,其操纵机构包括自动倾斜器、尾桨和发动机3部分。舵机是对这些操纵机构进行直接控制的重要设备,其性能的优劣直接影响无人直升机的飞行品质。一款合适的电动舵机有利于提高无人直升机飞行控制性能[2-3],因此,开展针对特定型号无人直升机使用的电动舵机控制器的研究具有重要的现实工程价值。
本文结合项目需求,针对一款最大起飞重量为700 kg中型无人直升机开展电动舵机控制器的设计实现。对该无人直升机对舵机的特殊需求进行了分析,提出了“DSP+FPGA+功率驱动”的硬件设计方案[4-6]。
1 需求分析与技术方案
1.1 需求与指标
本文旨在设计满足DWK700中型无人直升机使用的电动舵机系统。该系统包括舵机控制器1台、直线舵机3台以及旋转舵机2台。该无人直升机的尾桨和油门分别由2个舵机操控,通过钢索结构连接,连接关系如图1a所示;自动倾斜器采用传统十字盘结构,由3个直线舵机进行操控,每个舵机独立负责1路变距通道,舵机和连接器之间采用拉杆、球头和钢索连接方式,连接关系如图1b所示。

图1 尾桨、自动倾斜器舵机的连接
根据该型无人直升机对执行机构的技术需求,提出电动舵回路的主要性能指标如表1所示。
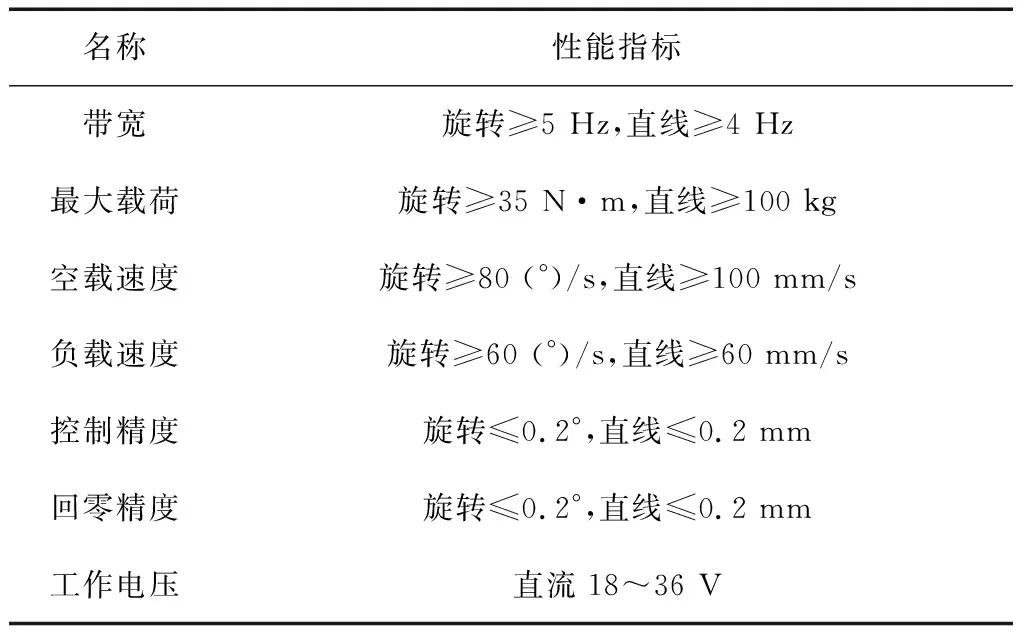
表1 电动舵回路性能指标
针对舵机控制器的设计需求,主要从软件和硬件2个方面进行分析。参考市场上成熟的舵机控制系统,采用DSP+FPGA的硬件架构,其控制器内部强弱电同时存在,在设计时要求做好强弱电分离;各部分核心部件模块全部采用标准化和模块化设计,需要注重部件的通用性和接口的可互换性。软件设计方面,为保证软件的质量和可维护性,其设计时应遵循软件设计规范,采用模块化的软件结构;软件运行发生故障时,为确保系统能够恢复到故障前状态,需对程序中一些关键信息采用余度设计。
1.2 硬件设计方案
本文采用DSP + FPGA作为主处理器,同时控制5路舵机,舵机控制器的硬件整体结构如图2所示。硬件部分可分为:主控单元、功率驱动电路、信号测量电路和电源电路4部分。其中每一路舵机单独占用,硬件设计基本相同。
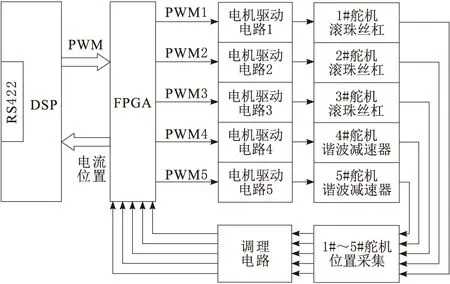
图2 舵机控制器结构
主控单元主要负责舵机控制算法的实现,为了使处理器具有快速计算能力、实现负载的算法,在选取DSP作为主控芯片的基础上,搭配FPGA来辅助采集传感器数据,减轻了DSP不必要的计算量。二者协同配合向驱动电路发出PWM控制信号,从而驱动舵机输出指定的位移或角度。测量电路对舵机的电流和位置进行实时监控,并反馈到主控单元,确保舵机控制的精确性。针对DSP+FPGA硬件架构内强弱电同时存在的特殊性,电源电路采取隔离供电的形式分别给传感器、驱动电路和主控单元提供电源。
1.3 软件设计方案
作为控制算法实现的载体,舵机控制器软件是整个系统设计的重要组成部分,其设计遵循了模块化和层次化原则。舵机控制器软件的整体架构如图3所示。
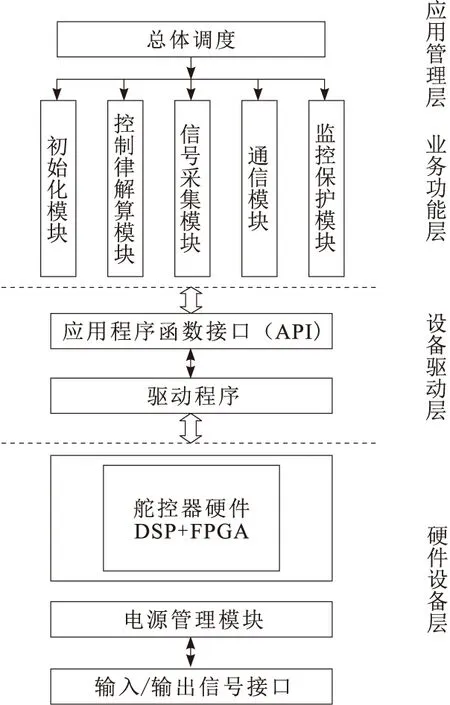
图3 舵机控制器软件架构
根据分层化原则,舵机控制器软件分为4层:硬件设备层、设备驱动层、业务功能层和应用管理层。模块化和层次化的设计原则使各模块之间相互独立,既便于调试和修改,又使程序更具拓展性和可读性。
2 对象建模与优化
2.1 对象建模
电动舵回路的建模主要分为4部分:无刷电机模型、功率驱动模块、减速传动机构和位置传感器。从重要性的角度出发,本文主要对电动舵机系统采用的永磁无刷直流电机进行建模分析。
本文以微分方程和传递函数2种形式建立无刷电机的模型。微分方程能完整体现模型的内部物理学关系,可以获取所有内部状态信号;传递函数能用简洁的方式体现模型输入输出之间的关系,在进行控制回路分析和控制器设计时比微分方程便利很多。Y型连接的无刷电机线电压方程为
(1)
uAB、uBC、uCA为电机三相线电压;R为三相绕组电阻;L为三相绕组自感;M为绕组间的互感;iA、iB、iC为电机三相相电流;eA、eB、eC为三相绕组反电动势。
无刷直流电机空载时的传递函数为
(2)
负载转矩和电机速度之间的传递函数为
(3)
KT为电机转矩系数;TL为负载转矩;Ω为电机机械角速度;J为转子转动惯量;Bv为粘性阻尼系数;Ud为直流母线电压;ra为绕组线电阻;ke为线反电势系数;La为绕组等效线电感。
无刷电机在电压和负载转矩共同作用下的传递函数模型为
Ω(s)=Gu(s)Ud(s)+GL(s)TL(s)=
(4)
综合可得,旋转舵机的整体传递函数为
(5)
直线舵机传递函数为
(6)
kpwm为功率驱动器的放大倍数;i为减速比;Kf为位置传感器系数。
2.2 辨识优化
电动舵机在运动过程中,受到外界负载扰动、内部摩擦力等因素的影响,舵机的精度、稳定性以及动静态特性也会产生相应变化[7]。通过理论建模只能大致确定舵机模型的结构,想要更进一步确定具体参数,需进行以实际测量数据为基础的舵机模型参数辨识[8]。
本文以旋转舵机为例,用最小二乘法进行参数辨识,其迭代公式为
(7)

由式(5)可知,舵旋转舵机的整体传递函数均为三阶模型,对其离散化后可得

(8)
并且,其对应的差分方程为
y(k)+a1y(k-1)+a2y(k-2)+a3y(k-3)=
b1u(k-1)+b2u(k-2)+b3u(k-3)
(9)
本文结合旋转舵机整体传递函数与其相关参数理论值,忽略与理论参考值相差不大的参数,对转自转动惯量J和线反电动势系数ke进行参数辨识。
通过理论计算得ra=0.562 Ω,La=0.444×10-3H,J=78×10-7kg·m2,kpwm=7.3,KT=0.047 9 N·m/A,ke=0.047 9 V/(rad·s-1),Bv=0.008 N·m/(rad·s-1),i=300,Kf=27.6。将其代入式(5)中得旋转舵机传递函数为
(10)
旋转舵机对应的差分方程系数辨识结果为a1=-1.139,a2=0.138 9,a3=1.838×10-5,b1=0.001 1,b2=0.002,b3=1.068×10-3,其对应的传递函数为
(11)
将不需要辨识的参数代入理论模型与实际辨识出模型比较,得出旋转舵机待辨识参数J=8.3×10-6kg·m2,ke=0.042 V/(rad·s-1)。
通过比较待辨识系统和辨识出的模型在同一信号源下的输出结果,验证辨识模型的精确度。给定频率为4 Hz、幅值为2°正弦信号,得到旋转舵机实际位置输出和辨识出模型的位置输出曲线如图4所示。从曲线可以看出,辨识出模型的位置输出与舵机实际输出曲线基本吻合,表明辨识出的传递函数精确度较高。
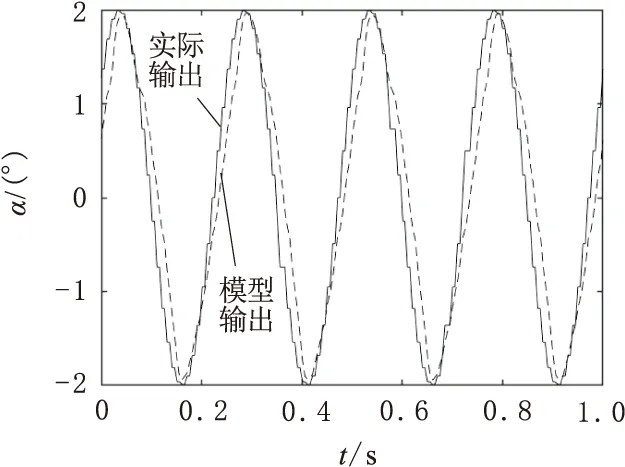
图4 旋转舵机实际位置输出与模型位置输出比较
3 控制方法研究
PID控制作为一种经典的控制算法,在工程领域广泛使用[9]。该算法对模型精度要求不是太高,参数整定较为容易且工程上也易于实现,但在舵机控制系统应用中存在负载动态变化时控制品质较差、小信号指令的控制精度不足和快速性与稳定性相矛盾等问题[10]。从控制对象存在的模型误差和未知干扰出发,结合工程的可实现度,本文将引入自抗扰控制器(ADRC)来提高系统的控制品质,其精髓在于它将影响被控对象的内外部干扰统一归结为系统总干扰并对其进行估算,在控制器输出量中对干扰进行补偿[11-13]。本文通过引入带宽的概念将ADRC改造成线性自抗扰控制器(LADRC),其结构如图5所示,减少了ADRC的设计参数[14]。
在传统的体育课堂中,都是教师引导课堂,学生配合着老师的指令完成体育动作,比如做健身操,各种活动前的锻炼等等。这种方法可能会导致学生对体育课堂失去兴趣,从而认为体育课枯燥无味,没有了学习的动力。因此,在体育教学中教师需要根据学生的实际情况,结合学生感兴趣的内容来改进自己的教学方法,体育课堂上需要创新来激发学生学习喜欢体育的兴趣,从而使他们自己主动的去锻炼。

图5 线性自抗扰控制器结构
本文采用三闭环串级控制结构,借鉴直流电机调速系统设计,电流环和速度环采用PI控制,位置环采用P控制。针对舵机负载动态变化的不确定性和小信号指令跟踪效果差这2类突出问题,在位置环引入线性自抗扰控制进行解决。
经设计,P控制下的位置环闭环传递函数为
(12)
Kw为速度环闭环放大倍数;Tw为等效惯性环节的时间常数;kfθ为位置环反馈系数。为使系统的阻尼比为1,kpp取1.25。
自抗扰控制器下的扩张状态观测器为

(13)

经扩张状态观测器补偿后,控制律为
u0=KP(r-z1)+KD(-z2)
(14)
z1、z2分别为舵机输出角度和电机输出角速度的观测值。系统闭环传递函数为
(15)
将设计的线性自抗扰控制器和PID控制器进行对比。额定负载状态下,分别给定小信号2°和大信号20°的阶跃信号,系统响应如图6和图7所示。2°阶跃信号下,LADRC上升时间为0.025 s;20°阶跃信号下,LADRC上升时间为0.03 s。当系统处于稳态时,LADRC无误差。采用PID控制时,系统到达稳态后始终存在误差。通过对比,可以得出无论大小信号,LADRC在应对外界负载时,系统性能都优于PID。

图6 2°阶跃信号下负载响应曲线
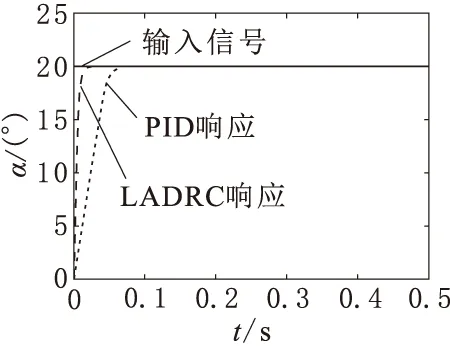
图7 20°阶跃信号下负载响应曲线
4 测试与验证
4.1 测试方案
电动舵机在实际使用中,需要和飞控计算机连接,实时响应飞控计算机的控制指令,并回馈舵机的位置状态信息。因此,在测试过程中,需设计舵机测试软件来代替飞控计算机进行控制指令的发送。直升机在飞行过程中,会受到铰链力矩的影响,舵机会时刻处在带载运行过程,而这个载荷是动态变化的。为了模拟这一实际运行状态,还需要设计负载加载试验台,提供可调负载。结合以上叙述,测试环境包括舵机测试软件、舵机控制器、电动舵机和负载加载台,如图8所示。
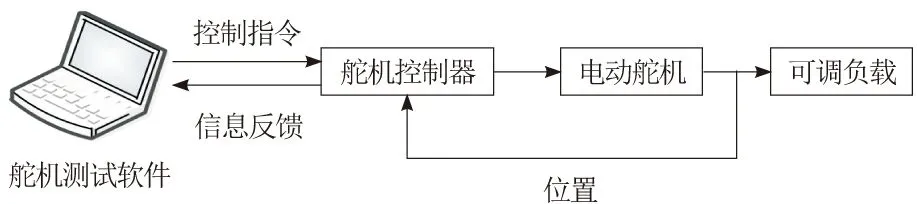
图8 测试验证的结构
基于Qt开发的舵机测试软件,其可以与舵控器进行通信、实时显示舵机运行状态信息、向舵控器发送舵机位置指令、提供特定信号源和数据记录等功能。
加载试验台主要作用是固定舵机,提供大小不同的负载。加载台上设置有专门的螺栓孔,采用相应螺栓即可对舵机进行固定。大小不同的负载采用液压杆来实现,液压杆设置多种不同大小的力,满足不同负载条件下舵机测试,可以充分测试舵机的负载性能。
电动舵机整体测试环境如图9所示。舵机测试软件发送指令信号,同时记录设定位置信号和反馈信号。测试完成后,对采集数据进行分析。

图9 舵机测试环境
4.2 测试结果
通过舵机测试软件发送舵机指令信号,分别给定30°、20 mm的阶跃信号,得到额定载荷情况下设定位置曲线和实际位置曲线如图10所示。

图10 30°、20 mm 阶跃信号
从阶跃响应曲线分析可以得出,额定载荷运行状态下,旋转舵机上升时间为500 ms,超调量为1.81%,稳态误差为0.11°;直线舵机上升时间为305 ms,超调量为1.23%,稳态误差为0.13 mm。
分别给定频率为4 Hz,幅值为2°、2 mm 正弦信号,得到给定位置曲线和实际位置曲线如图11所示。
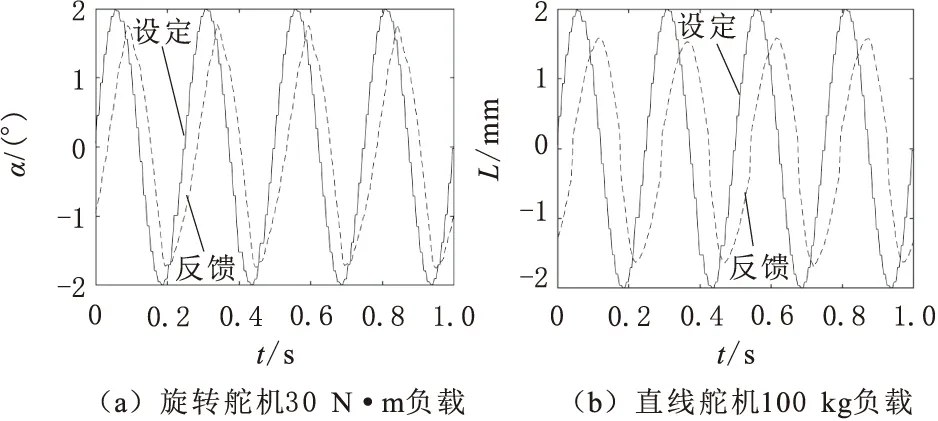
图11 2°、2 mm 正弦信号
从正弦响应曲线分析可以得出,额定载荷运行状态下,旋转舵机跟踪误差为0.11°,相移为16°;直线舵机跟踪误差为0.5 mm,相移为31°,满足实际使用要求。
4.3 工程试飞
目前,本文所研究的电动舵回路已经在DWK700无人直升机上进行安装,进行机上飞行测试。舵控器在DWK700无人直升机的实际安装如图12所示。

图12 机上舵机和控制器安装
在DWK700中型无人直升机航线飞行过程中,无人直升机进行了悬停、悬停回转和着陆等动作,过程中状态平稳。
同时,在试飞过程中,飞行控制计算机分别记录了俯仰舵机、滚转舵机、总距舵机和尾桨舵机在无人直升机起飞、小机动飞行、着陆等不同状态下的控制设定位置和反馈位置,如图13所示。
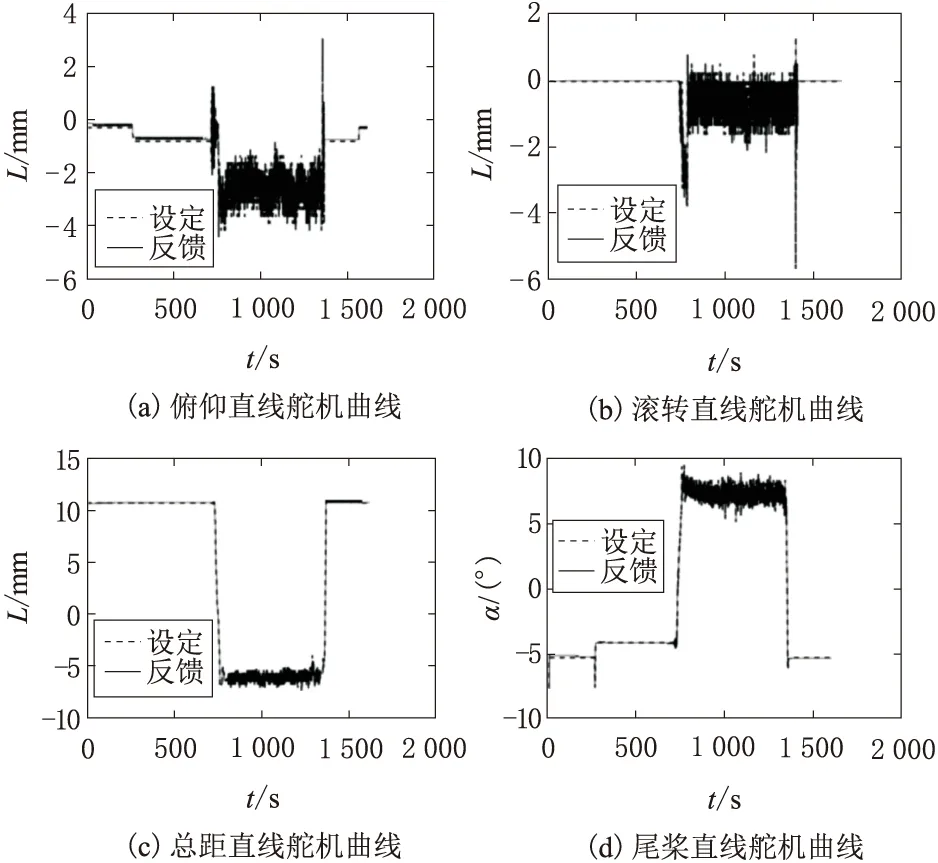
图13 电动舵机位置曲线
从图13中可看出,电动舵机跟踪性能良好、控制精度高,可满足无人直升机实际使用。
5 结束语
本文针对DWK700中型无人直升机对电动舵机的特殊需求,设计了一种以“DSP + FPGA”为主控单元的舵机控制器,来提高该无人直升机的控制性能。全文从需求分析、软硬件设计、建模与辨识优化和控制方法研究等多方面入手,提供一套详细的设计方案。经模拟测试和工程试飞表明,该舵控系统在稳定运行的基础上,解决了负载动态变化时控制品质较差和小信号指令的控制精度不足等问题,证实了该方案的可行性,取得了较好的工程应用效果,达到预期研究目标。

