基于CT和MRI的多模态医学图像配准算法

常锦才，张笑林，武伟娜，苏照，王雨暄，王嘉祺

( 1.华北理工大学 理学院，河北 唐山 063210；2.华北理工大学 3D建模与应用创新实验室，河北 唐山 063210；3.华北理工大学 基础医学院，河北 唐山 063210)

引言

图像配准提出的最初目的是为了对2幅或多幅图像进行图像融合，这些图像大多数来自于同一种成像原理下的同一物体，主要是对不同视角下的图像进行信息配准和拼接。随着科学技术的不断发展，各类传感器层出不穷，人们对图像配准的期望也不单单满足于简单的单模态和拼接功能，在大量应用场景和需求的催生下，针对同一物体，对不同成像原理而拍摄的图像进行配准，整合不同模态下图像的各类特征。多模态下的图像配准被广泛应用于多个领域，其中与医学影像学相结合的图像融合技术，已经成为了图像配准研究中的主流。

电子计算机断层扫描(CT)和磁共振功能成像(MRI)是目前的医学影像领域最为成熟，而且应用最广的成像方式。CT和MRI都是以DICOM格式进行存储的，这对图像融合和配准带来了便利。针对颅脑而言，CT成像可用于脑部肿瘤和血管的三维重建，MRI则主要是对脑内的神经纤维进行三维重建。二者图像的配准融合为医学工作者和研究人员提供了极大的便利。

1图像配准的基本框架

图像配准的基本框架包括以下4个方面：特征空间、空间变换、最优化搜索策略和相似性度量[1]。

特征空间的选取是图像配准工作的重点，一般也称为特征提取。通常情况下，特征空间的选择随配准算法而变化，不同的算法将具有不同的特征空间。比如，当配准算法以灰度值为基准，特征空间就可以选为图像中像素的灰度值；而大多数配准所采用的图像都是来自不同的图像设备，以灰度值为标准并不适用，这类算法在配准时可以选用图像空间位置上比较相近的点、边缘或者是曲线、曲面等。特征空间不仅关乎于算法的运行效率和结果，还影响算法的稳定性。大量的研究表明，理想的特征空间应该满足：特征提取简便快捷、特征匹配计算量小、特征数据量适宜，不受噪声、光照度等因素影响，且对各种图像均能使用。图1所示为图像配准框架。

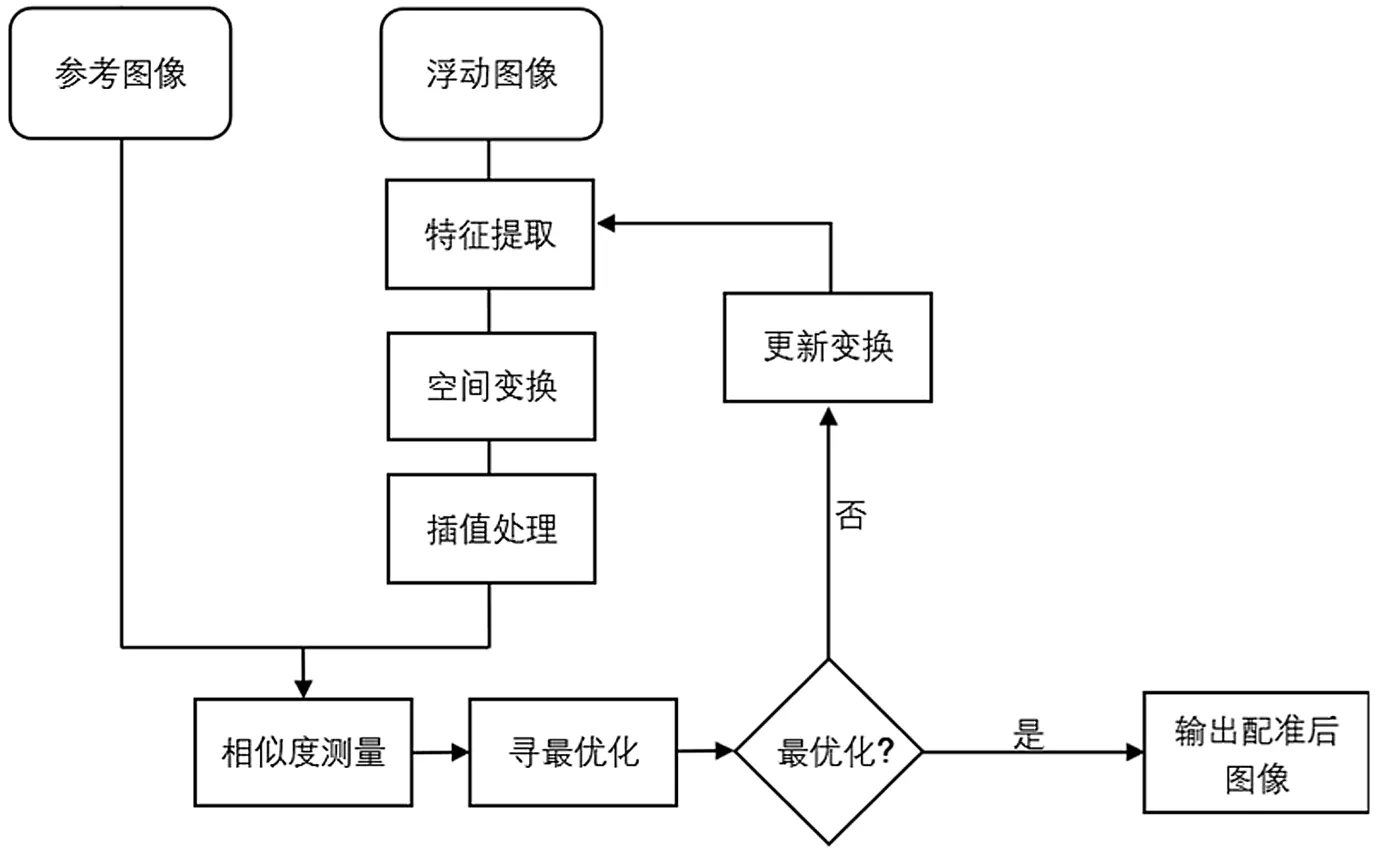
图1 图像配准框架

空间变换是指配准过程中图像变换的范围和方式，可以划分为全局变换、局部变换和位移场变换。其中全局变换的变换域最广，可以覆盖到整个图像上，但其变换效果往往不够精准。局部变换对全局变换进行了改进，可以对图像的关键点部位进行参数上的调整，而关键点以外的图像则使用插值算法进行处理。位移场变换精度最高，可以实现图像上每个像素点独立的参数变换，而这些变换则用一个巧妙的连续函数串联起来，从而实现整幅图像的变换。图像的变换方式基于其数学原理，线性变换一般指矩阵变换，主要是对图像进行旋转、平移、缩放等变换，能对图像实现基本的刚性配准。非线性变换的主要方式为多项式函数，能够实现图像的形变。在实际应用中，合理地使用空间变换能让配准算法事半功倍。

最优化搜索与相似性度量在功能上相辅相成，搜索最优的配准参数需要以2幅图像的相似度度量的数值为判断依据，它也直接反映了最优搜索策略的好与坏。实际的图像配准算法流程看似简单，但其背后却包含了大量的运算过程，选择一个高效快捷的寻优策略是降低运算的有效途径，最优化搜索方法种类繁多，但在进行寻优设计时，应该把眼光放到更快、更高效的算法上，理论数学由传统的贪婪算法出发，已经发展出多种最优化搜索算法，包括一维搜索中的试探法、函数逼近法；无约束最优化的梯度方法中的最速下降法、牛顿法、最小二乘法等；无约束最优化的直接方法中的模式搜索法、Powell法等。

相似性度量是图像配准过程中用来评判配准结果好坏的准则，相似度度量的数值直接反映了特征空间与空间变换算法的优劣，同时它也承上启下，它的数值也会反馈到搜索策略上，对搜索策略的选取具有重要意义。相似性的数学表达式如下所示：

(1)

公式中的xi，yi分别表示参考与浮动2幅图像的第i个像素的灰度值；xm、ym参考与浮动2幅图像的平均强度。针对不同的图像，配准算法也会有相似性度量。比如相关性是一种适用于单模态图像配准的相似性度量，它可以帮助研究人员了解浮动图像和参考图像之间的相似程度。相关性的数值直接反映了图像的相似程度，若数值为1，则表示2幅图像完全一致；若相关性的数值为0，则说明2幅图像完全不一致，图像可能来自不同物体，或相似性算法的选择出现问题。

2多模态医学图像配准常用算法

2.1 最大互信息配准算法

最大互信息配准方法与传统相似性度量之间的区别是，前者无视噪点的存在，也不必再对图像进行分割。互信息不需要对参考与浮动图像直接的强度关系进行初步假设，所以最大互信息配准方法被广泛应用于多模态图像配准工作，其强大的特性为配准工作带来了诸多便利，不仅适用于多模态图像的配准，面对破损的图像，互信息也处理得游刃有余。

互信息用于度量一个变量包含另一个变量的信息量或者2个随机变量的统计依赖性，它是信息论的基本概念，2个随机变量A、B间的互信息可根据信息论表示如下[3]：

(2)

式中，pAB(a,b)表示随机变量A、B的联合概率分布，pA(a)和pB(b)分别表示A、B的边缘概率分布。

同时，根据Shannon信息熵的定义：

H(A)=-∑pA(a)log2pA(a)

(3)

H(B)=-∑pB(b)log2pB(b)

(4)

(5)

(6)

(7)

上述公式中，H(A,B)表示条件A、B的联合熵。H(A)、H(B)分别表示A和B的信息熵，H(A|B)表示给定B的条件下A的条件熵，H(B|A)表示给定A的条件下B的条件熵，按照琴生不等式的概念，可以证明I(A,B)是非负的，则信息熵可以将互信息表示如下：

I(A,B)=H(A)-H(A∣B)

=H(A)-H(B∣A)

=H(A)+H(B)-H(A,B)

(8)

图2以维恩图的形式展现了边缘熵、条件熵和联合熵之间交并差集的关系。

图2 互信息的图形概述

综上所述，引入最大互信息的概念，应用到配准算法中，可以将既定的互信息测度定义为图像配准结果的判断依据，即配准图像之间的互信息达到最大值。此时作为随机向量的两图像系统的熵达到最小，也就是说2幅图像的不确定性己经很小了[4]。互信息的应用不仅缩减了配准所耗费的时间，也提高了算法的性能，因此，互信息被应用在许多图像配准过程中。

从概率的角度出发，当pAB(a,b)=pA(a)pB(b)，且I(A,B)=0时，条件A和条件B相互独立。当pAB(a,b)=pA(a)=pB(b)时，则称条件A、B完全依赖或者条件A、B完全包含，即H(A)=H(B)=H(A,B)，此时I(A,B)最大。互信息的基本性质如表1所示。

表1 互信息的基本性质

2.2 基于Canny算子和小波变换的最大互信息算法

John F. Canny于上世纪80年代提出了基于一种理论的最优边缘检测算子，称为Canny算子，虽然其自提出至今已有30多年，但却不影响其成为图像配准领域之中应用最广的边缘检测算法之一。Canny算法目标明确，首先要保证特征提取过程中的低错误率，其次要更好、更快地对位图像中的边缘点。由此引出了Canny算法的4个主要步骤：低通滤波降噪、有限差分法计算梯度幅值和方向、对像素点进行非极大值抑制、双阈值算法检测和连接边缘。

在数学领域，小波变换的提出为许多问题的解决提供了新方向，它也是傅里叶变换和短时傅里叶变换的一个重大突破，其优越的特性为图像处理领域开拓了新思路。小波变换的性能也优于传统的图像处理方法，其利用尺度函数和平移函数对函数或信号进行细化和分析，解决了许多傅里叶变换无法解决的难题。小波变换也因此得到了大量应用，尤其适用于近些年热门的图像处理研究。

由于小波变换的抗噪性很强，所以当Canny算子在图像边缘提取出来的是噪点时，小波变换无法在对应边缘提取出同样的噪点。因此，可以通过去除Canny算子提取的边缘图像中的噪声点，得到图像的边缘[5]。图3所示为边缘提取算法的流程图。

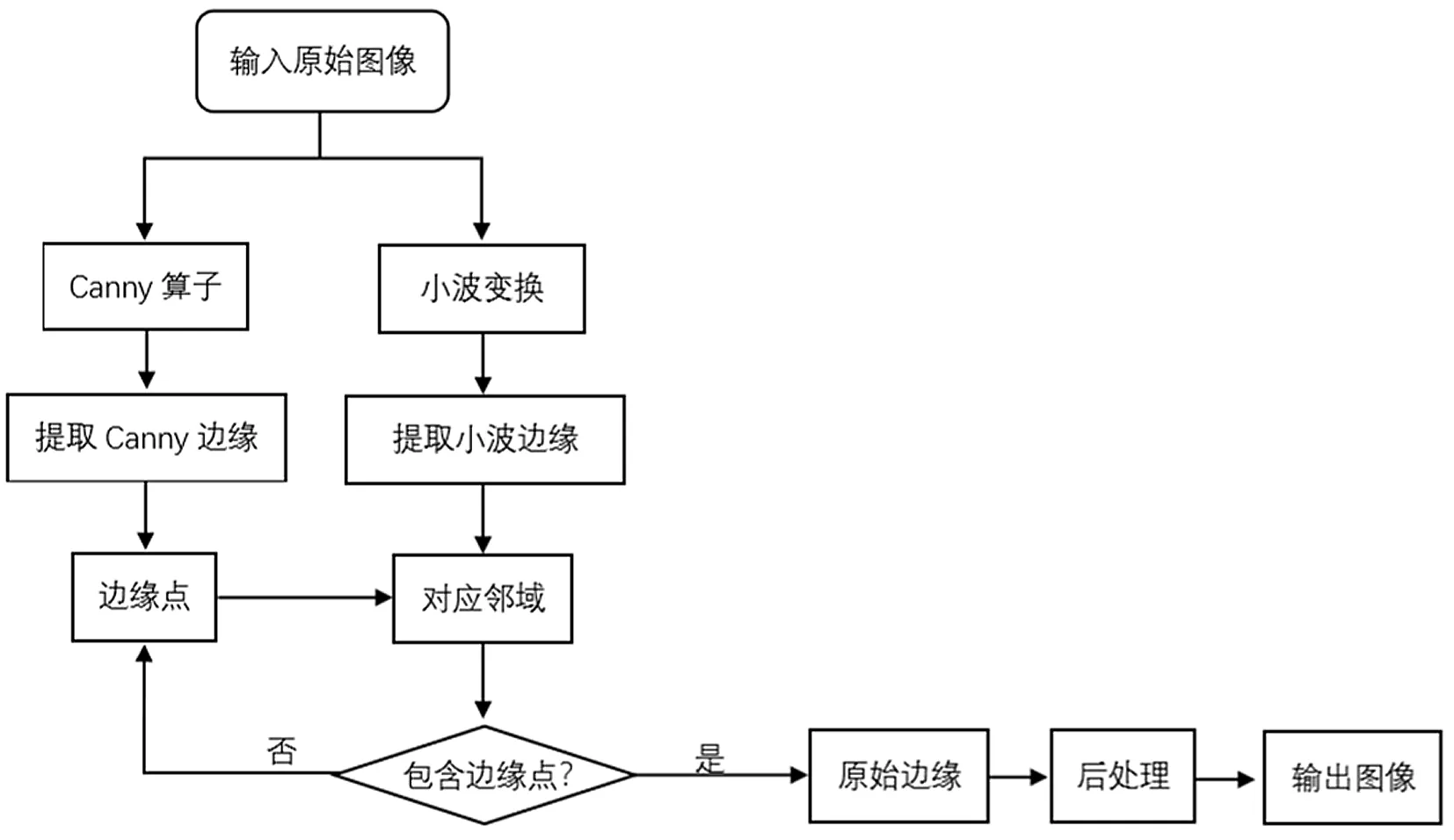
图3 边缘提取算法流程图

2.3 基于轮廓金字塔的归一化互信息图像配准算法改进

对于灰度值分布不均匀，甚至分布比较极端的图像，传统算法一般很难处理。由于小波变换引入了多尺度的概念，可以利用不同尺度的图像进行多尺度分析，从而提高了配准的精度和效率，使图像得到良好的配准处理。

轮廓金字塔是小波变换在图像处理领域针对序列图像而提出的一种多尺度策略，通过对图像进行模糊处理或下采样，达到对序列图像进行配准的目的，下采样的图片由下至上，层层递减，堆叠起来的序列图像就如图金字塔一般，故而成为轮廓金字塔算法。使用CT和MRI图像进行一次多模态医学图像配准，并给出轮廓提取和下采样金字塔的图像依据和理论概述，从图像的角度对算法进行一个粗略的剖析。Canny算子具有优质的边缘检测能力，可以对CT和MRI分别进行轮廓提取，下采样金字塔自下而上隔行隔列地降低分辨率，使算法所需算力呈指数级下降。最后给出如图4所示配准前后的对比图。

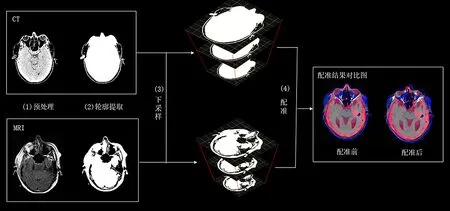
图4 配准前后的对比图

图4流程图左上角的图像为CT数据，左下角为MRI数据，从左到右分别对图像进行了预处理、轮廓提取、下采样和图像配准，右侧是配准结果对比

3基于3D Slicer平台的图像配准

3.1 图像配准模块简介

3D Slicer为学术研究人员和医疗从业者提供了众多关于针对图像配准和图像融合的模块，这些模块包含大量算法和算法测评规则。

3.1.1 General Registration(BRAINS)

General Registration BRAINS(以下简述BRAINS)是一种基于ITK的颅脑图像互信息配准程序，算法过程完全实现自动化[6]。该模块的开发源自BRAINSFit项目，其初衷是为多模态的三维图像进行配准。

对比ITK内的算法，BRAINS模块功能全面，不仅包含各种类型的变换方式，且能对内部函数进行优化。图5为BRAINS模块的内部选项栏。在配准前输入参考图像和浮动图像，在Percentage of Samples一栏可以调节配准的精度，默认为0.002，可以设置参数为0.2(20%)以获得高细节。

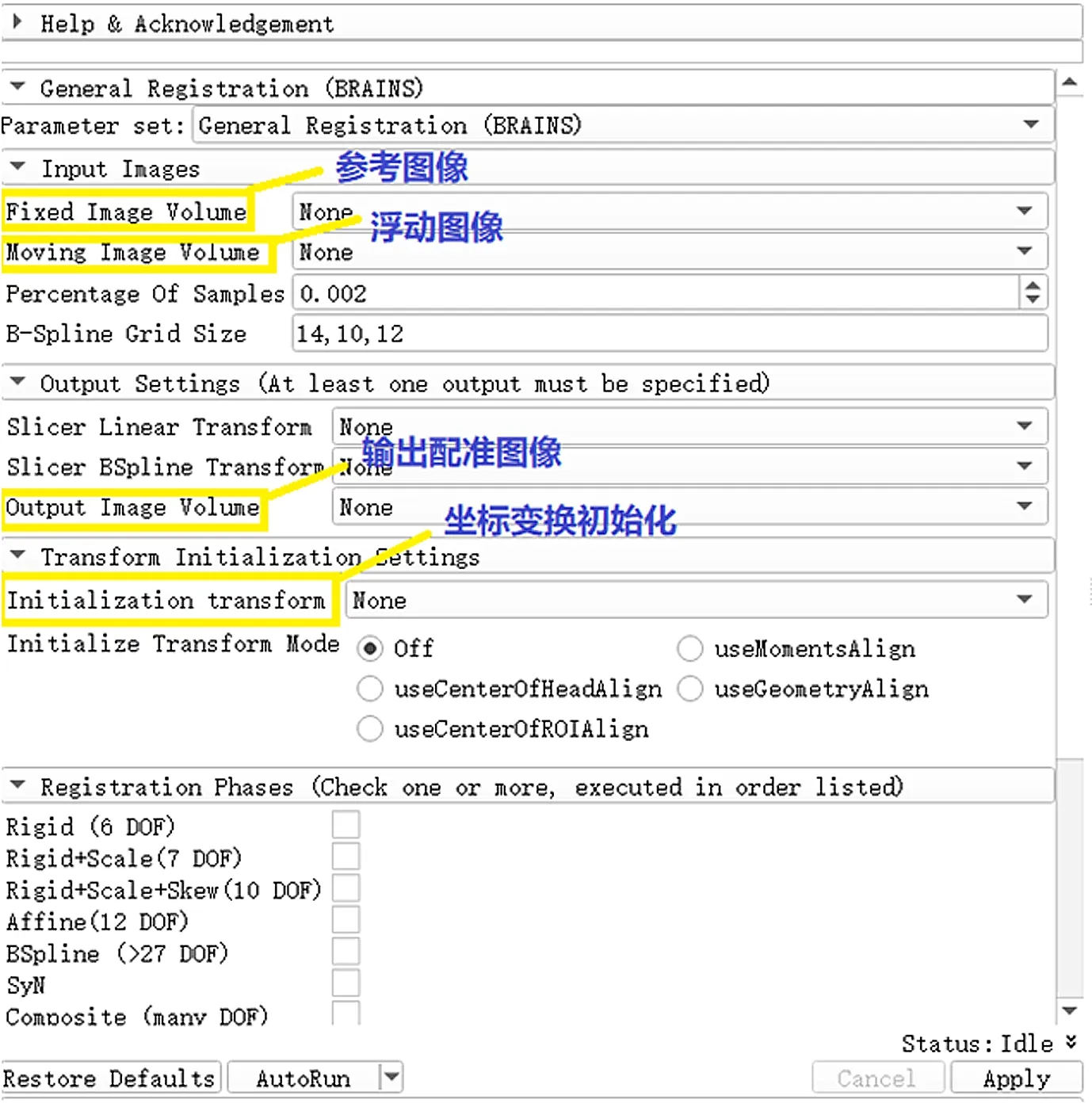
图5 General Registration功能展示

3.1.2 General Registration(Elastix)

General Registration(Elastix)模块依托于Elastix软件，Elastix是一款基于ITK的开源软件。该软件由一组通常用于解决医学图像配准问题的算法组成。Elastix的模块化设计允许用户快速配置、测试和比较特定应用程序的不同注册方法，命令行界面通过脚本支持对大量数据集的自动化处理[7]。现在Elastix有了SimpleElastix，使得它可以在C++、Python、Java、R、Ruby、C#和Lua等语言中使用。

3D Slicer中的Elastix去繁从简，只保留了全自动的图像配准功能，去除了类似于BRAINS模块中复杂的参数设置，降低了使用门槛，配准过程迅速快捷。图6所示为配准前后2幅图像的对比结果，由图9可以看出，Elastix采用的是非线性变换，且对配准图像进行了图像融合。

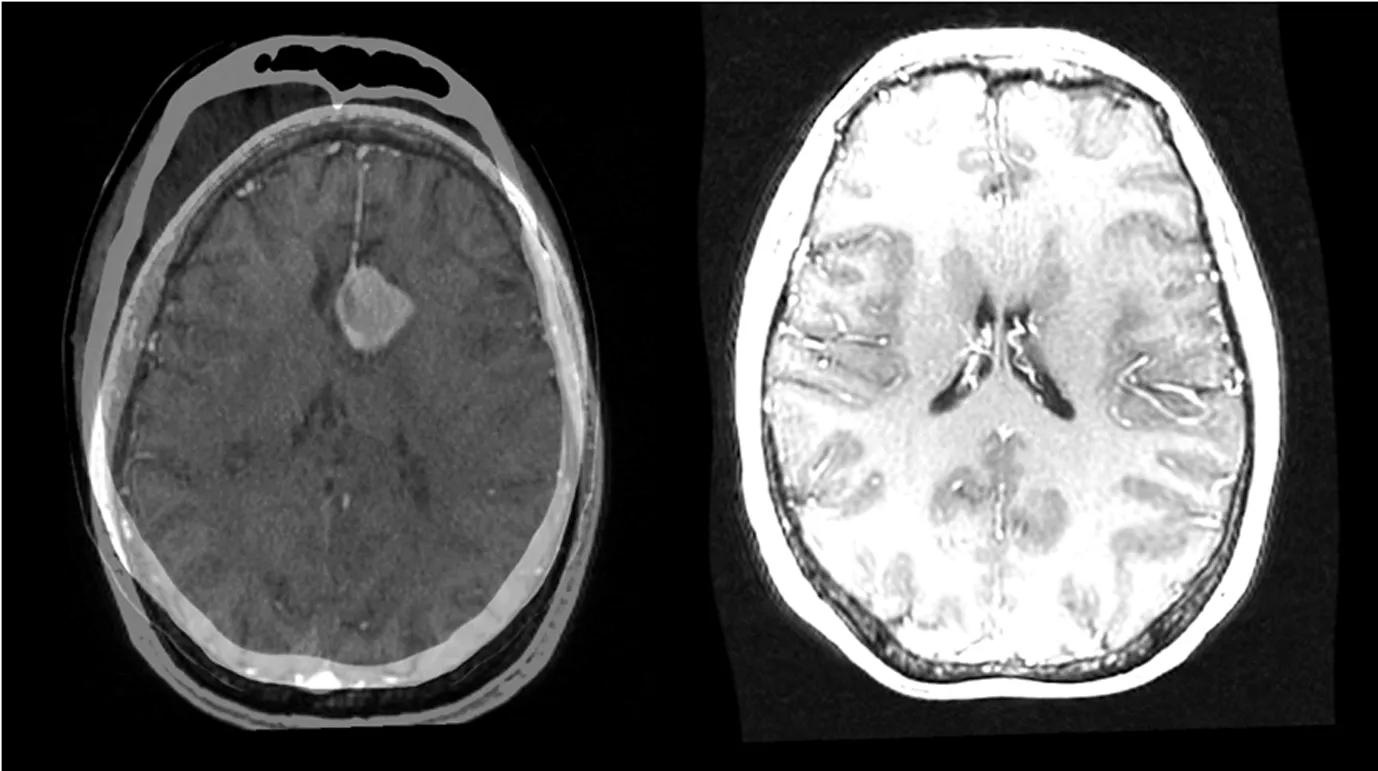
图6 Elastix模块配准结果前后对比图

3.1.3 Landmark Registration

Landmark Registration的主要功能是实现参考图像与浮动图像之间的手动配准，从而得到图像之间的变换参数，该模块对图像类别没有限制，适用于多模态图像的配准。

Landmark Registration模块的另一个优点是具有实时性，打开模块后，输入参考图像和浮动图像，选择变换类型，然后在模块中添加基准点(Landmark)，通过调整图像中的基准点使图像重合。图7所示为Landmark Registration示意图。

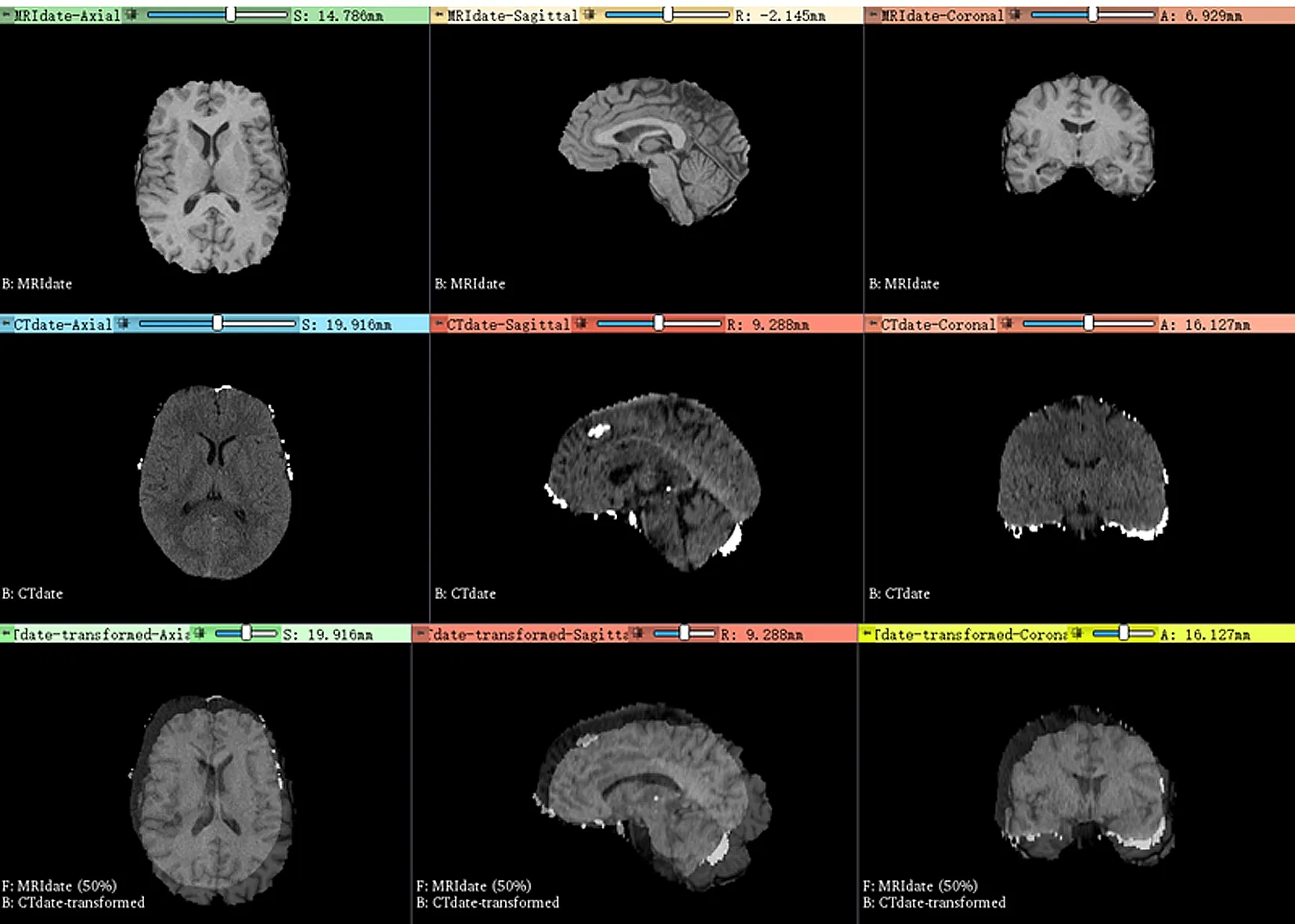
图7 Landmark Registration示意图

3.1.4 CheckerBoard Filter

CheckerBoard Filter模块可用于对比配准结果。它的功能是基于参考图像与浮动图像，创造出一个新的棋盘图像，输出图像将显示2个图像之间的相似度，浮动图像和配准图像之间被重采样到相同的原点、间距和方向。模块的使用不受图像类别的限制，适用于检测多模态图像配准的结果。图8所示为CheckerBoard Filter选项栏展示。

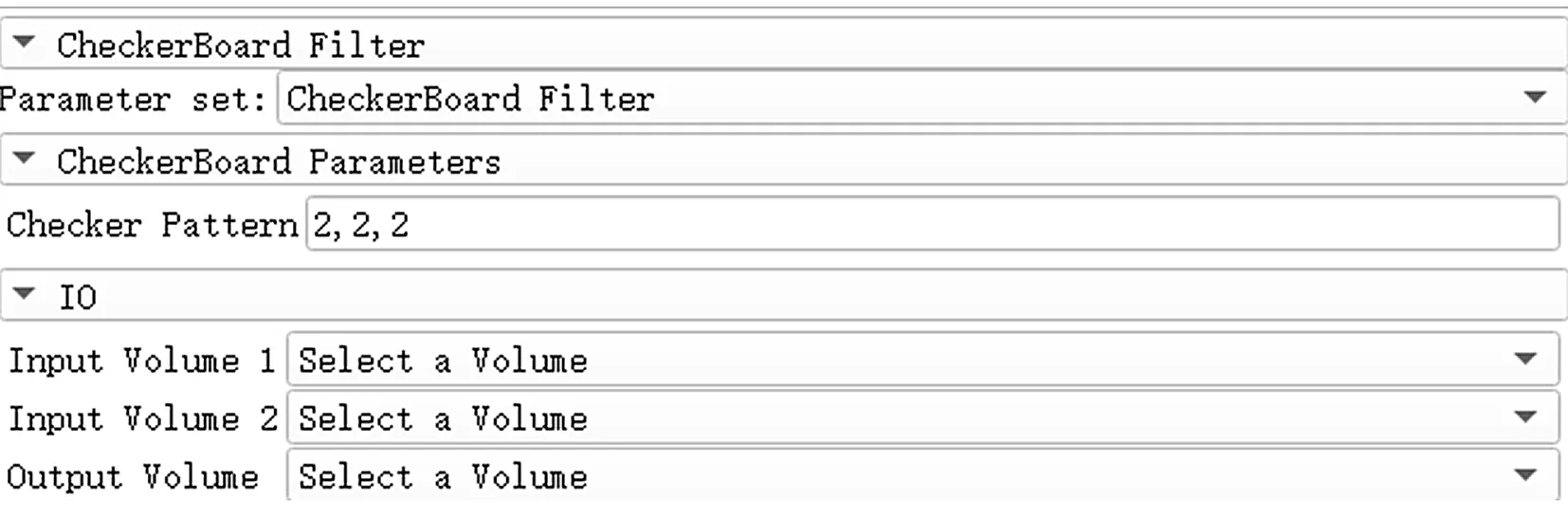
图8 CheckerBoard Filter选项栏展示

图9为冠矢轴示意图，CheckerBoard Parameters中Check Pattern的参数表示使用者可以从水平位、矢状位和冠状位3个维度对图像进行切分重组。数字代表切分后的像素块，1代表不切分。比如2，2，1是指在前2个维度进行切分，而第三个维度不进行切分。结合医学上3个位面的定义图与CheckerBoard的结果，图10所示为CheckerBoard示意图，可以清晰地看到模块如何根据参数进行切分。

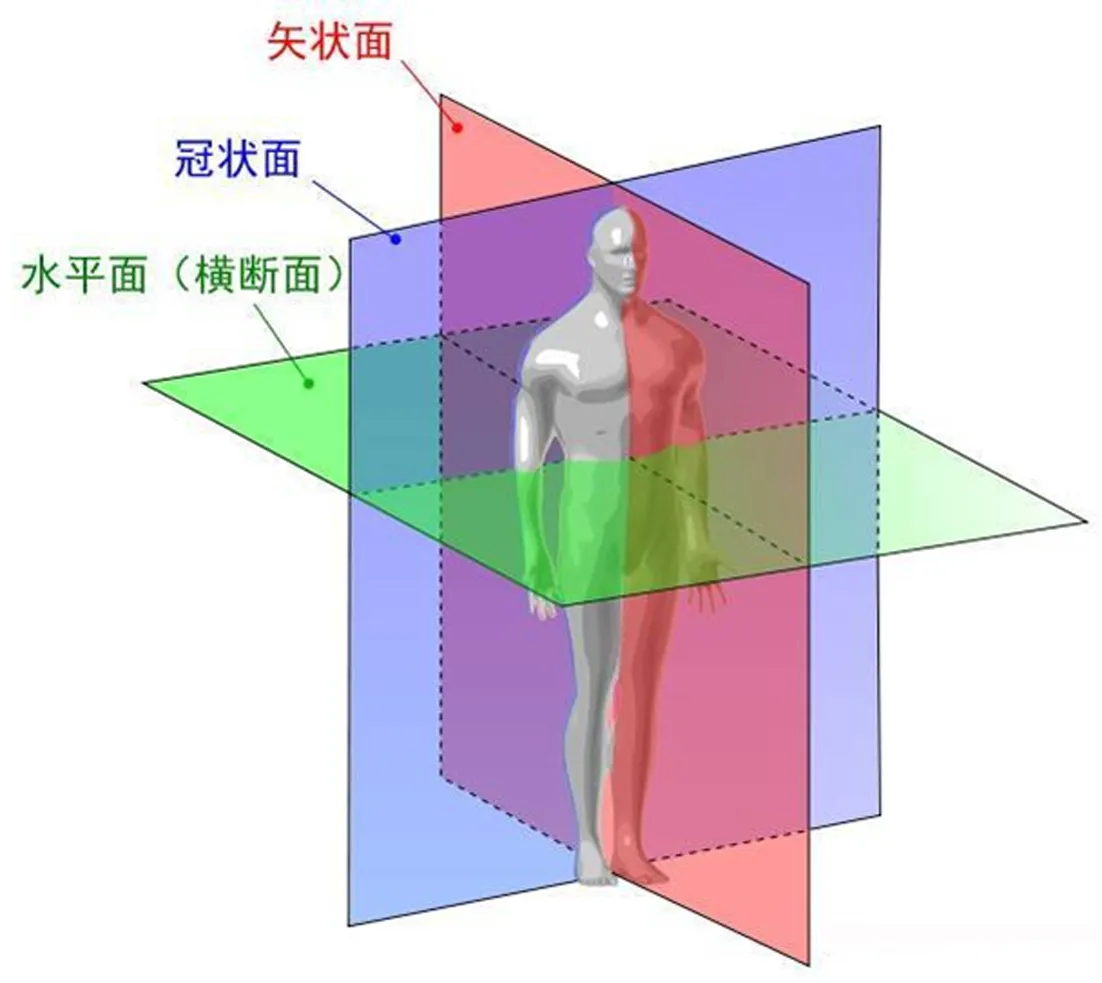
图9 冠矢轴示意图

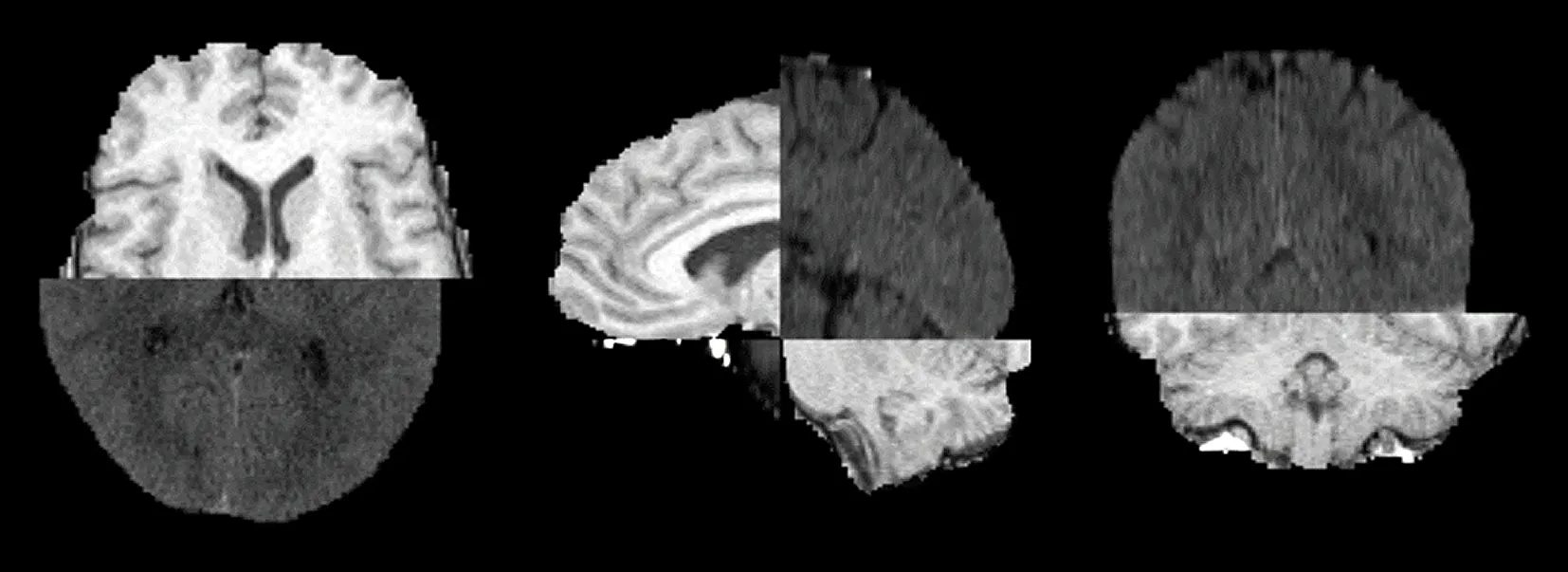
图10 CheckerBoard示意图

3.2 图像配准实例

图11所示为配准流程图。

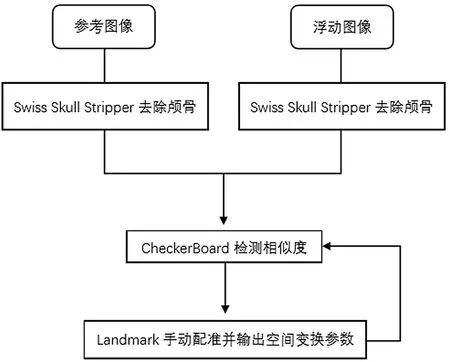
图11 配准流程图

3.2.1配准图像准备

图像来源于软件自带的样本数据，选用CT和MRI的图像。首先要对数据进行预处理，使用Swiss Skull Stripper模块去除颅脑以外的部分，只保留颅脑可以使图像的轮廓更加清晰，这样方便在后续的手动配准进行操作。图12所示为MRI图像去除颅骨前后的对比图。

图12 颅骨去除前后对比

3.2.2相似度检测

使用CheckerBoard Filter模块，对去除颅骨后的CT和MRI图像进行相似度检测，Check Pattern参数设为4、4、4。图13所示为2幅图像的原图像和切分后重组的棋盘图像的对比图。这幅图像较好地展示了模块的切分效果和2幅图像重采样得到的原点、间距和方向都不尽相同。

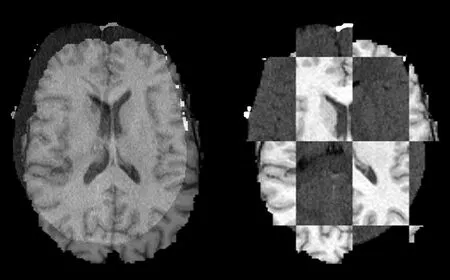
图13 图像配准前相似度检测

3.2.3配准实现

打开Landmark Registration模块，输入MRI图像作为参考图像，输入CT图像作为浮动图像。点击Apple，进入下一步操作。在空间变换中使用仿射配准(Affine Registration)，插入基准点(如图14所示)后，手动移动基准点，可以实时地观测到重叠部分的图像随基准点的移动而移动。参考4.2.3的模块介绍，可以看到2幅图像在3个维度上都实现了配准。

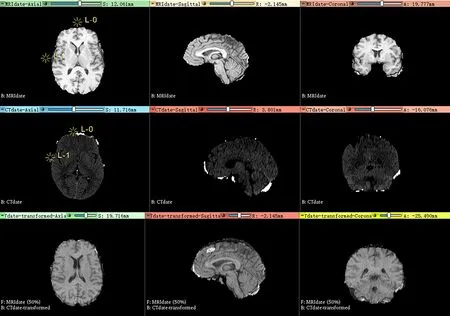
图14 插入基准点后的变换结果

配准效果满意之后，模块会自动保存根据调整基准点得到的变换，再打开Transform模块，对图像进行变换，得到配准图像。如果没有对图像变换这一步，则得到的只是变换，而不是图像。

3.2.4配准结果检测

得到配准后的图像后，再使用CheckerBoard模块进行相似度检测，2次检测的结果如15图所示，由图15可以看到,配准结果较好。至此，完成了基于CT和MRI的多模态图像配准，也得到了配准后的浮动图像。可以看到配准后的图像轮廓清晰可见，配准效果较好。

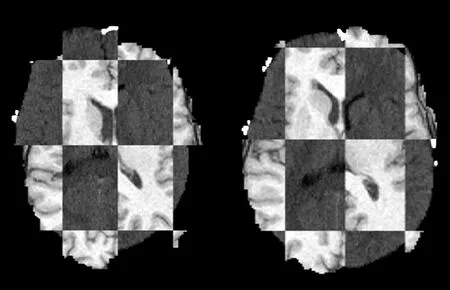
图15 配准前后的棋盘图像展示

4结论

(1)二维层面的算法配准，其原理类似于最优化原理中的寻优过程，重点是特征空间和最优搜索空间的选取。医学图像配准工作的开展是为了后续的图像融合和对融合后的图像进行三维重建，所以算法还需要更加快速高效。

(2)3D Slicer 是一个极其强大的医学影像处理开源平台，多种功能模块的开发为医学图像配准提供了更多的可能性。软件的熟练掌握也避免低效率的底层开发。

(3)探索完成了图像配准和融合，以及融合后三维模型的重建。直观的三维模型，摆脱了以往手术方案制定平面化的短板，让患者的病情一目了然，这为术前的手术方案制定和术中的穿刺导航都提供了极大的便利。