二层规划求解的精确罚函数蚁群优化算法

冯力静，陈丽芳，刘洋

(华北理工大学 理学院，河北 唐山 063210)

优化问题[1]具有重要的实际应用价值，备受研究者关注。现实生活中大量生产管理系统均具有递阶特征，递阶优化问题亦称多层优化问题，其求解是NP难题[2]。多层规划的几何特性比单层规划要复杂得多，其中二层规划具有多层规划的典型特征，能够有效代表多层规划问题，因此，该项目从二层规划入手，研究其特征及求解方法，为多层规划求解探索一条研究路径。二层规划与单层规划相比有3点本质的不同：(1)上下层决策变量互相影响制约；(2)结构非凸；(3)非处处可微。这些特征为二层规划求解带来了极大困难。即使所有函数均是线性函数，也是NP难问题。赵礼阳等[3]提出了二层线性规划的极点算法，求解过程通过对上层目标函数值的排序，避免了盲目验证极点，提高了求解效率；余谦等[4]提出了粒子群和单纯形法相结合的一种混合粒子群优化算法解决二层线性规划问题，通过初始种群可行化，控制步长，淘汰不可行粒子等方法避免了罚函数处理约束的困难，提高了算法性能；范宏等[5,6]分别使用了跟踪中心轨迹内点法和萤火虫算法结合的混合算法及原-对偶内点法和森林算法对交直流混合输电网最优潮流和电力系统无功优化的二层规划问题进行求解，并为算例进行仿真计算，验证了这些算法在解决实际问题时的可行性；程林鹏等[7]通过下层K-T条件代替下层问题，将二层规划问题转化为单层规划问题，再采用基于Pareto最优解集的萤火虫群优化算法对其求解，从而避免了算法过早陷入局部最优，通过实例测试表明了算法可行有效；张涛等[8]提出了基于人工蜂群算法求解二层线性规划问题，数值试验表明，算法可在较短时间内得到问题的近似最优解；解丽等[9]提出用博弈思想的讨价还价模型将二层线性规划的最优解进行有效化，以此求得问题的Pareto有效解。学者们把粒子群算法、萤火虫智能群优化算法应用到二层规划寻优问题中，对二层规划的算法做了相应的研究，取得很多研究成果，但未考虑上下层全局优化，因此，该项研究拟从全局优化角度解决问题。

蚁群优化算法(Ant Colony Optimization，ACO)采用选择、更新、合作等分布式并行计算机制，具有良好的搜索性能和较强的鲁棒性，在解决典型组合优化问题时显示出明显的优越性，目前对蚁群算法在数学理论、算法改进、实际应用等方面的研究[10-17]是计算智能领域的热点。

罚函数法[18-20]是解决约束优化问题的一种重要、有效的方法，通过在原有目标函数加上由约束函数组成的惩罚项迫使迭代点逼近可行域，把约束优化问题转化为一个或一系列的无约束优化问题，通过研究无约束问题来解决约束优化问题。但一般罚函数存在计算上的序贯性缺陷，难以直接应用。

为了更好地解决二层规划问题，该研究将改进蚁群算法应用于二层规划全局寻优处理，进而推广到多层规划问题中。考虑到二层规划系统一般带有约束条件、加大了求解难度，设计一种新的精确罚函数法处理二层规划问题的约束条件，并将处理过程嵌入蚁群算法流程，编程仿真二层规划问题的全局寻优，并通过实际问题验证该算法的有效性。

1二层规划(BLP)的描述形式

(1)

其中：F，f：Rn1+n2→R，Rn1+n2→Rm1，g；Rn1+n2→Rm2，X，Y分别是Rn1和Rn2的凸子集。

公式(1)，下层以最优决策反应上层，是二层线性、非线性规划的理论及算法的研究出发点，该研究以此为对象进行研究。

2优化算法设计

2.1 精确罚函数

在解决非线性约束最优化问题时，一般采用罚函数法，它能够将非线性约束优化问题转化为无约束优化问题，使得问题求解更加容易。

在应用经典罚函数时，随着罚因子的变化会引起Hesse矩阵的病态，给无约束最优化的求解带来障碍，同时，经典罚函数在计算上的序贯性为研究人员的计算应用带来了困难。精确罚函数，有效地避免了在计算方面的序贯性，并且使约束最优化问题的解直接"精确"地成为该罚函数的某个极小点，因此简化了问题的求解过程。

不等式约束问题如公式(2)：

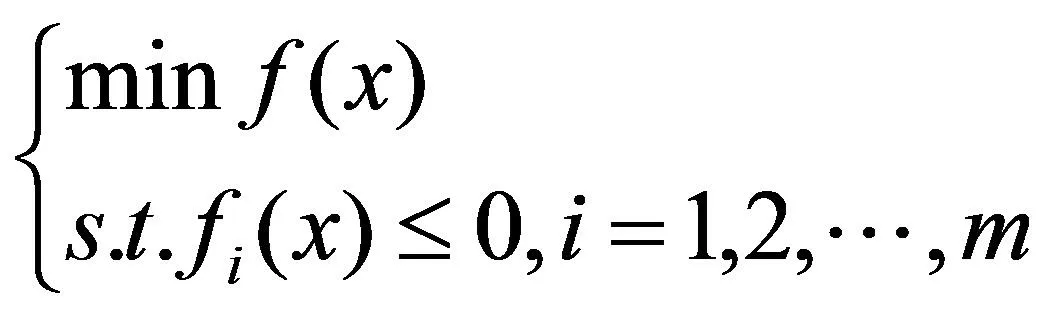
(2)

定义一种新的精确罚函数，公式(3)：

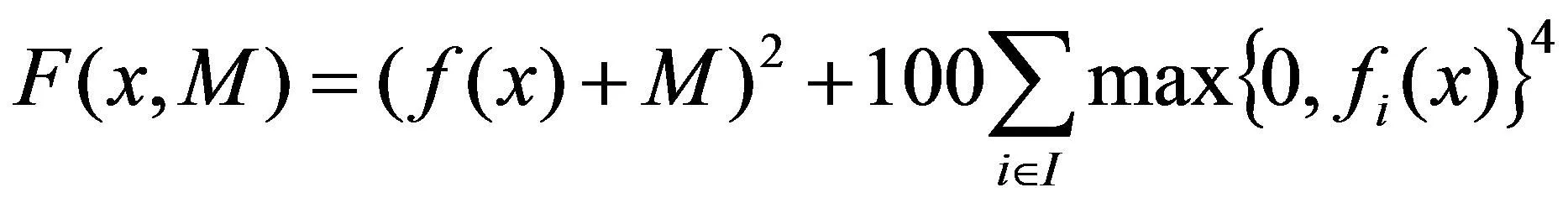
(3)

把有约束问题公式(2)转化为公式(4)的无约束罚函数优化问题：

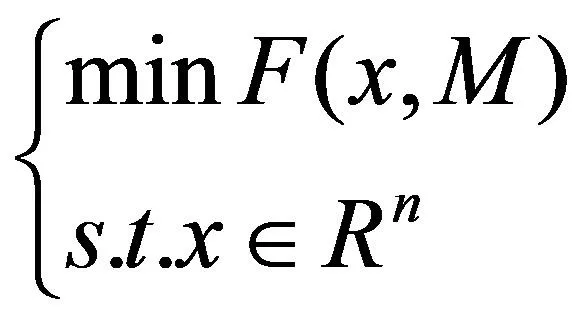
(4)

如果对于某一个M，无约束罚函数优化问题的最优解也是原不等式约束优化问题的最优解，那么则称M为精确罚参数，F(x,M)为精确罚函数。

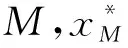
2.2 改进蚁群算法

蚁群算法具有分布式并行计算机制，在处理离散优化问题时，信息素是以离散的方式存储的；当求解二层规划的连续优化问题时，信息素仍然离散地分布到各条路径上，但对解空间的划分方式与基本蚁群算法不同，对于连续函数最小优化问题，直接求解；对于连续函数最大优化问题，必须要经过变换，将其转换成在[0,1]上的函数最小优化问题minf(x)+C，其中x∈[0,1]，加常数C的目的是为了使目标函数值大于0。

具体实施过程如下：

(1)解空间的划分方式：h为自变量x要求精确的小数点位数，用h个十进制数近似表示自变量x，构造由h×10+2个"结点"组成的路径图，分h+2层，第一层和最后一层分别为起、终结点且仅含一个结点，记为0。中间包括h层，分别代表x的十分位、百分位、……，这些结点中，相邻层之间具有连接通路。蚂蚁m需逐层游走，不得跨层，所走过的路径用式(5)解码计算得到相应的自变量x(m)。

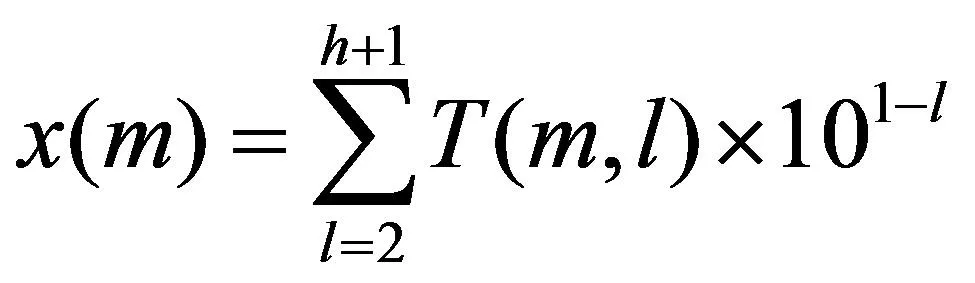
(5)

每只蚂蚁第一步均为T(m,1)=0。(蚂蚁m第l步所在的结点用T(m,l)表示)。

(2)设蚂蚁总数为M0，蚂蚁依次通过第一层，第二层……直至最后一层。蚂蚁m当前所在的结点为T(m,l-1)=a，蚂蚁根据式(6)来选择下一个结点。

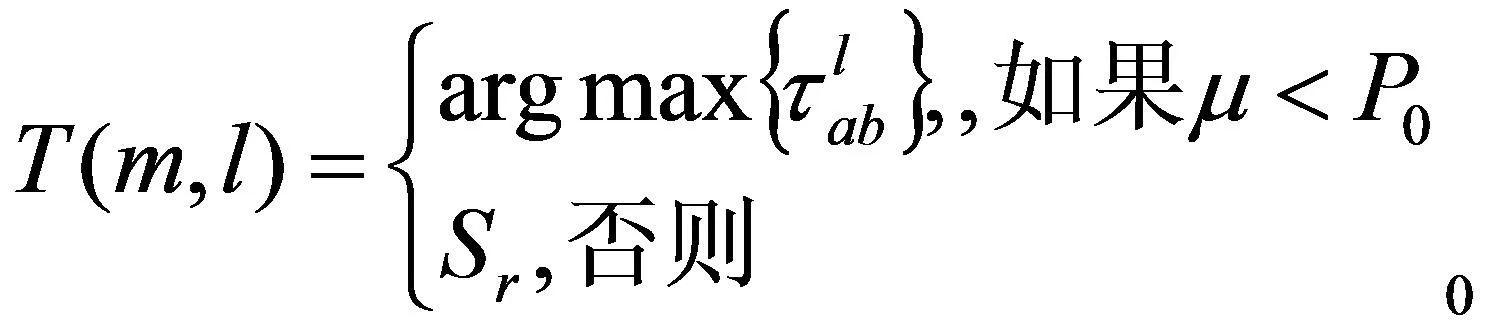
(6)

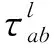
(3)根据式(7)计算每个结点被选中的概率，选择下一结点的概率利用遗传算法中的转盘法，生成Sr，其中Sr表示用伪随机选择来确定下一步要走的结点。

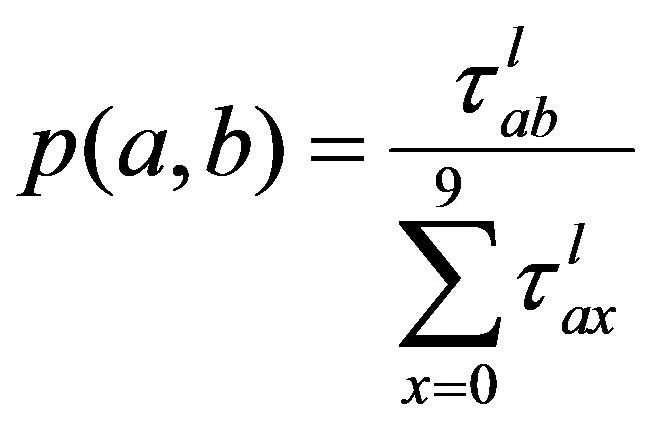
(7)

其中P(a,b)表示从当前结点a转移到下一层结点b的概率。这个公式仅允许蚂蚁在有上一层结点时才允许其向下一层转移，这是改进蚁群算法区别与其它蚁群算法之处。所有蚂蚁按上面的步骤到达h+1层后，均选择转移到最后一个结点0上。

(4)蚂蚁在游走过程中要按照式(8)不断改变经过路径上的残余信息素，通过残余信息素量的大小引导下只蚂蚁路径的选择，经过多次循环之后，得以确定一条最优路径。之后进行局部残留信息素的更新：

(8)

其中ρ表示路径上残留信息素减弱的速度，通常取定为[0,1]区间上的一个常数，τ0是信息素的初始值，也是一个常数。

(5)所有蚂蚁按式(1)～式(4)完成一次循环，利用式(5)解码蚂蚁 选择的路径，并计算出第 只蚂蚁经解码之后对应的自变量取值。算出每只蚂蚁所对应的函数值，并由式(9)选出函数值最小的蚂蚁：

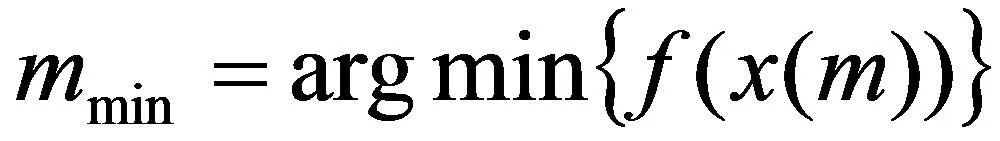
(9)

(6)对函数值最优的这只蚂蚁所经过路径上的信息素按式(10)全局更新：

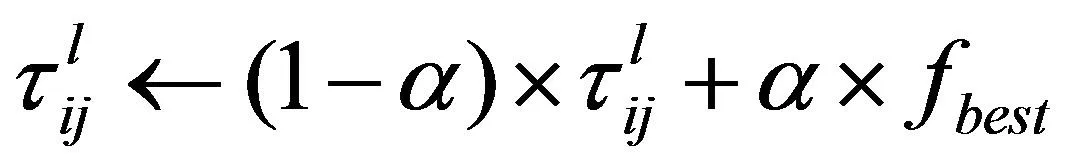
(10)

其中：i=T(mmin,l-1)，j=T(mmin,l)，l∈[2，h+2]，a是一个[0,1]上的常数，fbest为最优蚂蚁所对应的函数值。

(7)重复式(1)～式(6)，当达到指定的循环次数或得到解的最小值在一定循环次数后没有改进，说明求得最优解，算法结束。

2.3 优化处理步骤

Step1：依据标准解确定解空间，做归一化处理，利用精确罚函数公式(4)，通过选择合适的罚因子M处理上层约束问题。

Step2：应用改进的蚁群算法求解上层决策变量值。

Step3：将每个上层决策变量的值，带入到下层，下层问题转换成一元连续函数优化问题，利用公式(4)处理下层约束，嵌入蚁群算法计算下层决策变量。

Step4：将下层最优决策变量反馈到上层进行寻优，达到循环次数程序结束，输出计算结果。

3仿真实验

由于算法中的参数选择尚无严格的理论依据，该研究采用一些文献提供的方法得出参数的一般合理范围，初始参数范围为：α=0.2～0.8；ρ=0.4～0.9；P0=0.5～1，在此基础上进一步优化。算法的各个参数，利用仿真实验通过不同参数对算法运行结果的影响，讨论分析参数值的选择。

该项研究采用经典的实验方法，控制一个参数变化、保持其他参数不变，经过反复训练仿真，最终获得参数最优组合为：α=0.8，ρ=,0.8，P0=0.8，τ0=0.01，h=7，M0=20，M=2，运行循环次数：1 000，程序采用VC++编程实现。

以下面的二层规划问题为例：

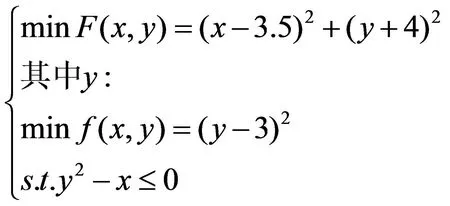
(11)

将数据输入后，平均时间小于1，得到运行结果为：上层决策变量x=0.999 999，上层决策变量y=0，最优函数值为22.25。表1所示为不同算法求值比较。

表1为理论最优解与文献[21]及该项研究算法(P-ACO)进行对比，发现P-ACO算法在相当短的时间内得到明显优于文献[21]的求解结果且改进了理论最优解和最优值。

表1 不同算法求值比较

4实际应用

4.1 价格控制问题描述

政府为规范价格变动所采取的各种调节和干预措施即为价格控制问题(Price Control Problem)。一般分为直接干预和间接调节方式。对价格行政管理较多的国家，采取直接干预的措施较多；对价格行政管理较少的国家，采取间接调节的措施较多。

价格控制问题是一类具有鲜明实际背景的二层规划问题，模型如下：

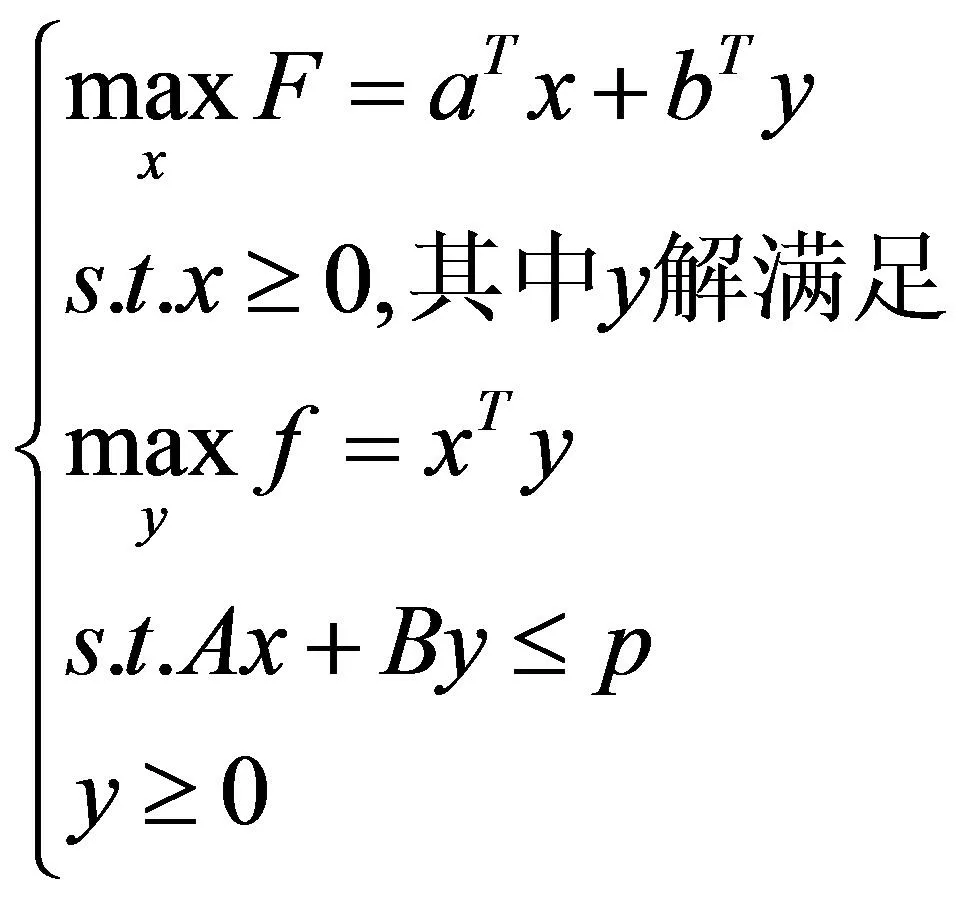
(12)

其中：a，x，b，y∈Rn，P∈Rm，A，B∈Rn×m，Rn表示示n维实数空间。该模型的几何意义是：下层决策者的目标函数的价值系数x由上层决策者为了优化其自身的目标函数而确定。决策变量y又由下层决策者决定，上层决策者又根据下层进一步调整价值系数x，以使其目标函数最优。分析税收、补助金规划和地区性的废水废气处理，确定最优方案主要利用这个模型。

4.2 模型构建及方案优化

分析上述问题，构造数学模型如下：

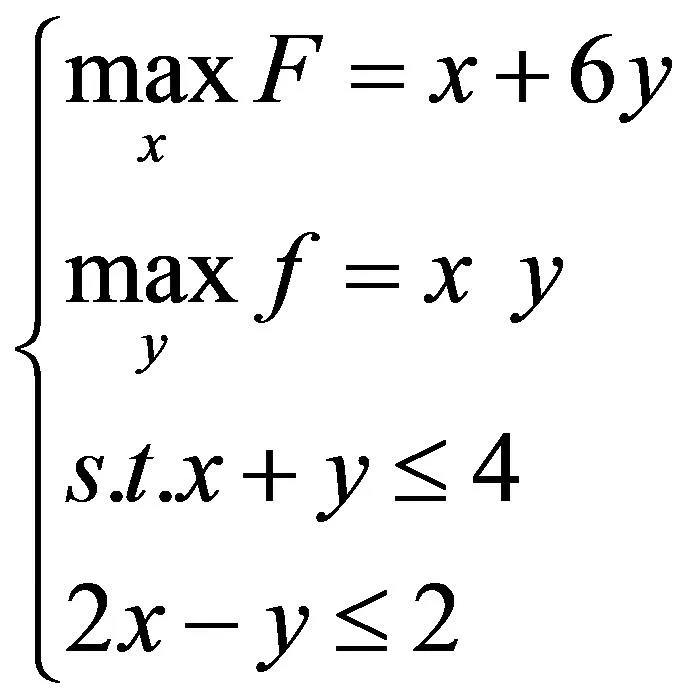
(13)

其中y为(x给定时)下层规划的解。

运用线性二级价格控制问题的单纯形法[22]求解，可得(0,4)为问题的最优解，该解的实际意义是：上级部门按产品定价x=0给下级部门，下级部门生产y=4个产品为最优方案。这样的方案可以使上级部门获利最大为F=24。而下级部门收益却为0。这样的最优方案，很难调动生产部门的积极性，在现实生活中明显不可取。

利用该研究提出P-ACO算法，处理流程如下：

(1)由于本问题属于约束最大优化问题，应用本算法时，需先将其转换为约束最小优化问题。

(2)上层属于无约束最优化问题，依据标准解确定上层决策变量 的取值范围为[0,1]。下层变量y做变换y-2，构造F(x,y)=10-x-6(y-2)，应用精确罚函数处理约束。

(3)利用P-ACO算法，运行程序，结果,x=0.999 999，y=0.998 325，F(x,y)=15.0 253。

结果分析：运行结果的含义解释：x=1，y=3其实际意义为：上级部门按产品定价x=1给下级部门，下级部门生产y=3个产品为最优方案。这个方案虽未能使上级部门获利最大(15<24)，但在考虑利润的同时兼顾了下级部门利益，能够充分调动下级部门员工的生产积极性，比单纯形法求得的(0,4)方案更符合实际，用于指导生产决策更加科学合理。

5 结论

(1)提出基于精确罚函数的蚁群优化算法，实现了二层规划问题的优化求解。设计了一种新的精确罚函数处理约束条件，避免了一般罚函数不可微、不光滑的问题，加快算法的收敛速度。

(2)采用改进的蚁群优化算法进行二层规划上下层组合求解。

(3)通过数值实验、实际价格控制问题决策对算法进行验证，编程对整个优化计算过程进行仿真。该研究成果，为二层规划决策、多层规划问题求解提供了一种新的研究思路。