基于支持向量回归的房价数据分析

卢超猛，马泽众，韩阳，郭小强

(1. 华北理工大学 理学院 唐山市工程计算重点实验室，河北 唐山 063210；2. 华北理工大学 学科建设处，河北 唐山 063210)

支持向量回归(Support Vector Regression, SVR)是支持向量机(Support Vector Machine, SVM)在回归领域的应用，分类和回归是SVM主要解决的两类问题。其中支持向量分类( Support Vector Classification, SVC)在国外的研究已经趋近成熟[1]，而SVR还有很大的发展空间，国内对于SVM的研究起步较晚，目前还在发展中[2-3]。

数据处理是数据挖掘的重要一步，海量的原始数据中存在着大量不完整(有缺失值)、不一致、有异常的数，严重影响到数据挖掘建模的执行效率，甚至可能导致挖掘结果的偏差，所以进行数据清洗就显得非常重要。统计发现[4]，在数据挖掘的过程中，数据预处理工作量占到了整个过程的60%。房价预测在社会、经济方面有着重要的作用。通过对房价的分析预测，可以为政府的宏观控制、企业战略制定以及个人的需求等方面带来巨大的价值[5-6]。

针对已经做过部分预处理的房价数据集，通过分析数据的特性，对数据分别做了重复值处理、异常值处理以及使用主成分分析(PCA)进行数据降维[7]。该项研究主要采用了支持向量回归算法进行数据的分析，为了保证分析结果的可行性以及直观性，分别选取了普通线性回归算法、贝叶斯岭回归算法和梯度增强回归算法作为对比算法。对于训练后的模型，需要对其进行评估和测试。选取均方误差(MSE)、平均绝对误差(MAE)、绝对系数(R2)、差异解释得分(EV)对模型进行评估。选择了均方根误差(RMSE)、MAE、平均绝对百分比误差(MAPE)、EV对模型的应用效果进行评估[8-10]。

1理论基础

通过实验来分析SVR算法在房价数据中回归分析的表现，同时也需要选取对比算法进行对比实验。在选取对比算法的时候，首先需要选取比较经典的多维度情况下的普通线性回归算法，然后又选取了较为成熟的贝叶斯岭回归算法作为进一步对比，最后选取了相对较新的梯度增强回归作为对比。以期得出全面可靠的研究结论。下面是几种算法的原理概述：

(1)普通线性回归

随机y与x1,x2,…,xk的线性回归模型为：

y=β0+β1x1+β2x2+,…,+βkxk+ε

(1)

其中β0,β1,β2,…,βk是k+1个位置参数，β0称为回归常数β1,β2,…,βk称为回归系数。y称为被解释变量，x1,x2,…,xk是k个精确可控制的一般变量，称为解释变量。

(2)贝叶斯岭回归

岭回归估计公式：

A(k)=(XTX+kI)-1XTY

(2)

其中，k称为岭参数，I是与样本维度相同的单位矩阵。由于假设X已经标准化，那么XTX就是自变量样本的相关阵。如果Y也经过标准化，那么计算的结果就是标准化后的岭回归估计。当k=0时，岭回归估计A(0)就是普通最小二成法的估计值。

(3)梯度增强回归

算法思想是，首先使用一个初始值来学习一棵决策树，叶子处可以得到预测值，以及预测之后的残差，基于前面决策树的残差来学习后面决策树，直到预测值和真实值的残差为零。最后前面许多棵决策树预测值的累加即是测试样本的预测值。主要优点有：

a. 可以灵活处理各种类型的数据，包括连续值和离散值。

b.相对SVM来说，在相对较少的调参时间情况下，预测的准备率也可以比较高。

c. 使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如Huber损失函数和Quantile损失函数。

GBDT的主要缺点是由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。

(4)支持向量回归

SVM是1995年基于统计学习的理论基础发展而来的一种通用的新的学习方法，解决了第二代神经网络的结构选择和局部最小值(过拟合、欠拟合)等问题。以统计学习为理论基础的支持向量机现被应用于机器学习的各个领域，称为最通用的万能分类器。

支持向量机是结构最优风险理论的一个算法实现。该算法涉及的主要步骤及数学理论有：

a. 最大间隔超平面的计算；b.拉格朗日乘子；c. KTT条件与对偶变换；d. 高维映射；e. 核函数与软间隔。

通过实现以上步骤及数学原理，使线性分类器可以应用到非线性的数据集中。

2波士顿房价数据集的回归分析

介绍了普通线性回归、贝叶斯岭回归、梯度增强回归等作为对比的算法以及该研究中所使用的支持向量回归算法的原理。根据其原理，选取数据集后，对数据集进行下一步的回归分析。

2.1 数据集选择以及数据导入

研究所采用的数据来自经典的波士顿房价数据集。然后根据数据集的数据采取了以下数据处理方法。

(1)重复值处理

在获取数据的时候经常会有一些重复的数据，而重复的数据会对统计结果产生影响，也会误导决策人员的决策。使用python中已经编写好的duplicated函数，其会对所有列进行对比，如果某两行每一列的值都一样时会标记为重复值。

(2)异常值处理

Z=(X-μ)/σ

(3)

其中：μ为总体平均值，X-μ为离均差，σ表示标准差。z的绝对值表示在标准差范围内的原始分数与总体均值之间的距离。判断Z-score得分是否大于2.2(此处2.2代表一个经验值)，如果是则是True，否则为False。将判定结果为true的数据行直接删除。

(3)主成分分析(PCA)降维处理

将数据的自变量由13维降至9维，PCA降维的过程分为以下几步：

a. 将数据集输入模型；b. 对数据集进行转换映射；c. 获得转换后的所有成分；d. 获得各成分的方差；e. 获得各成分的方差占比；f. 取方差最大的前9项。

2.2 模型评估方法

对预测模型进行性能评估是至关重要的，一般是从模型的准确度和训练时间等方面衡量。对于不同的模型选择合适且有效的误差分析方法均有不同。该研究采用常用的均方根误差、平均绝对误差和平均百分比误差3项指标评价模型的性能。

(1)均方误差(Mean Square Error，MSE)

(4)

范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

(2)平均绝对误差(Mean Absolute Error，MAE)

(5)

范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

(3)均方根误差(Root Mean Square Error，RMSE)

(6)

式子，也称为标准误差，表示误差的平方的期望值，能够反映一个数据集的离散程度。n为模型测量的次数。

(4)平均绝对百分比误差( Mean Absolute Percentage Error，MAPE)

(7)

范围[0,+∞)，MAPE 为0%表示完美模型，MAPE 大于 100 %则表示劣质模型。从公式来看，MAPE跟MAE具有相似性，差别主要在分母的位置。当真实值有数据等于0时，存在分母0除问题，该公式不可用。

(5)绝对系数(R-Square，R2)

(8)

越接近1，效果越好。R2的含义，是从最小二乘(就是2次方差)的角度出发，表示实际y值的方差有多大比重被预测y值解释了。

(6)差异解释得分(Explained Variance score，EV)

(9)

当残差的均值为0时，它与R2是一样的。

3支持向量回归在房价预测中的应用

针对采用的波士顿房价数据集，首先完成了数据的预处理步骤。然后通过分析对比回归算法的原理和理论，确定了该数据集应用到选取的回归算法上的过程以及方法。该研究对于模型评估的部分理论也进行了分析与阐述。将数据集载入算法中构建模型，随后应用该模型对预留的测试数据进行测试评估，进而得出其回归分析的效果以及模型的各项表现。

3.1 数据导入和数据处理

经过重复值、异常值处理以及PCA降维操作，得出可导入算法的数据。在进行回归预测分析时，通常需要将已知的数据集分为训练集和测试集。训练集用于模型的训练以及生成，而测试集则用于测试已训练好的模型的真实预测效果，从而得出其预测的准确率。

图1为SVR模型与训练数据的拟合图，其中虚线为原始训练集，实线为利用训练集训练出的SVR模型对训练集的各个数据的预测结果。

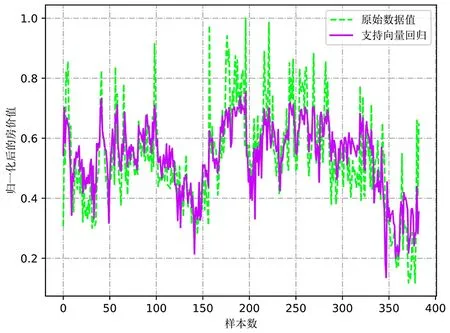
图1 SVR模型与训练数据的拟合图

由图1可知，SVR算法的回归分析具有一定的效果，但是仅仅通过观察图示无法得出准确结论。因此，需要采用模型评估算法对模型进行评估。表1即为模型评估的误差分析详情，采用了MSE、MAE、EV、R24种评估方法分别对模型的训练效果进行评估。

表1 模型评估误差分析表

通过表1可以看出，效果较好的模型为梯度增强回归。在用模型对训练数据进行拟合时，支持向量回归的效果略差。而以梯度增强为代表的其他回归算法，由于其在训练模型时，会对错误进行多次学习，因此对训练数据的预测效果较好。

然而真正能够体现其回归预测效果的是其对未知数据的预测，也即图2中模型对测试数据集进行预测时的拟合对比图。图2中点状数据即为测试集的原始数据值。其他数据线即为各个模型的预测结果值。

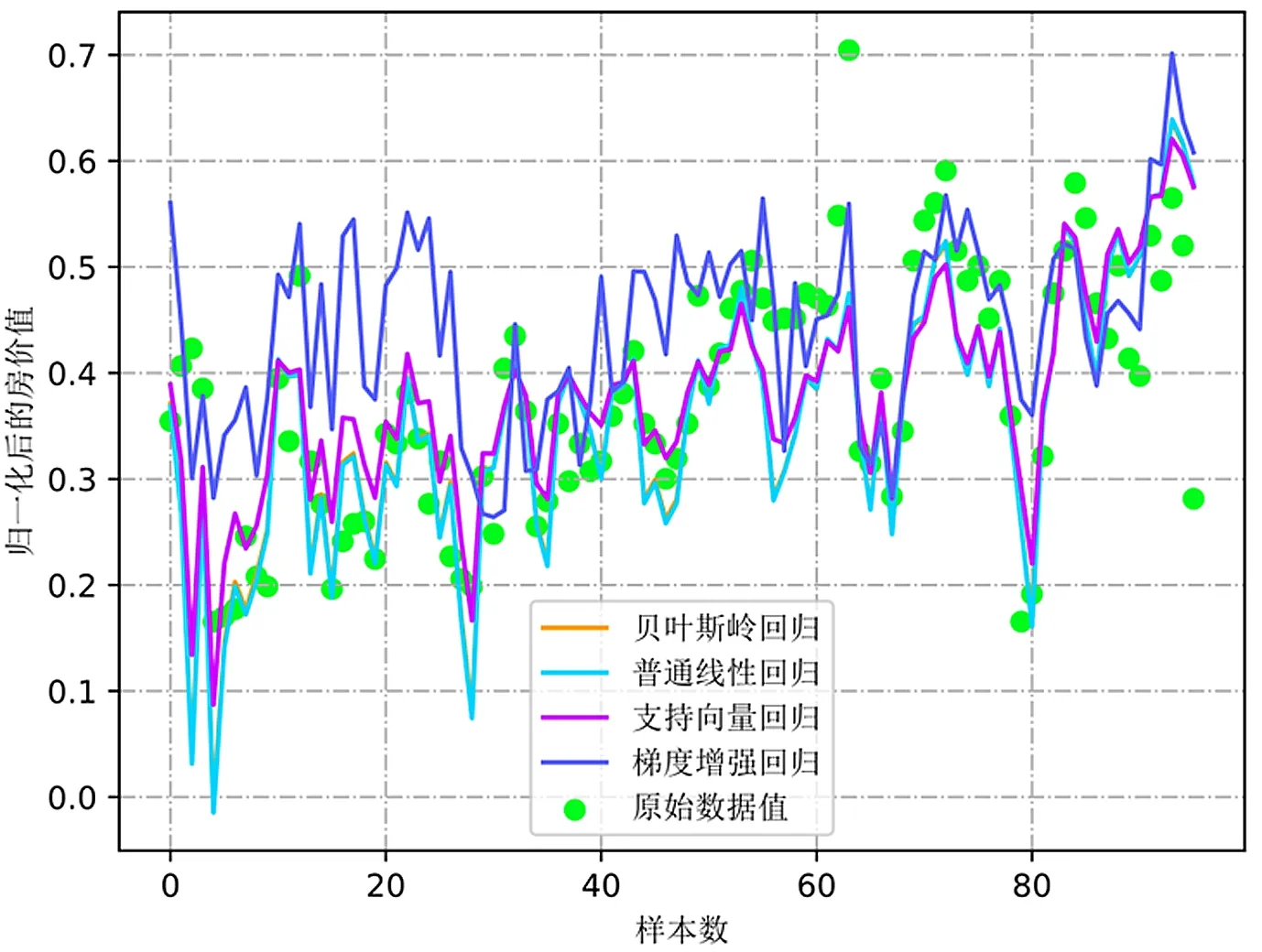
图2 各个模型与测试数据的拟合对比图

由图2可以较为直观地看出，作为本实验的重点研究对象的SVR模型表现较为良好，相较于其他回归算法，其表现出更好的拟合效果。为了更加清晰地单独观察SVR模型，图3为SVR模型与原始测试集的单独对比图。

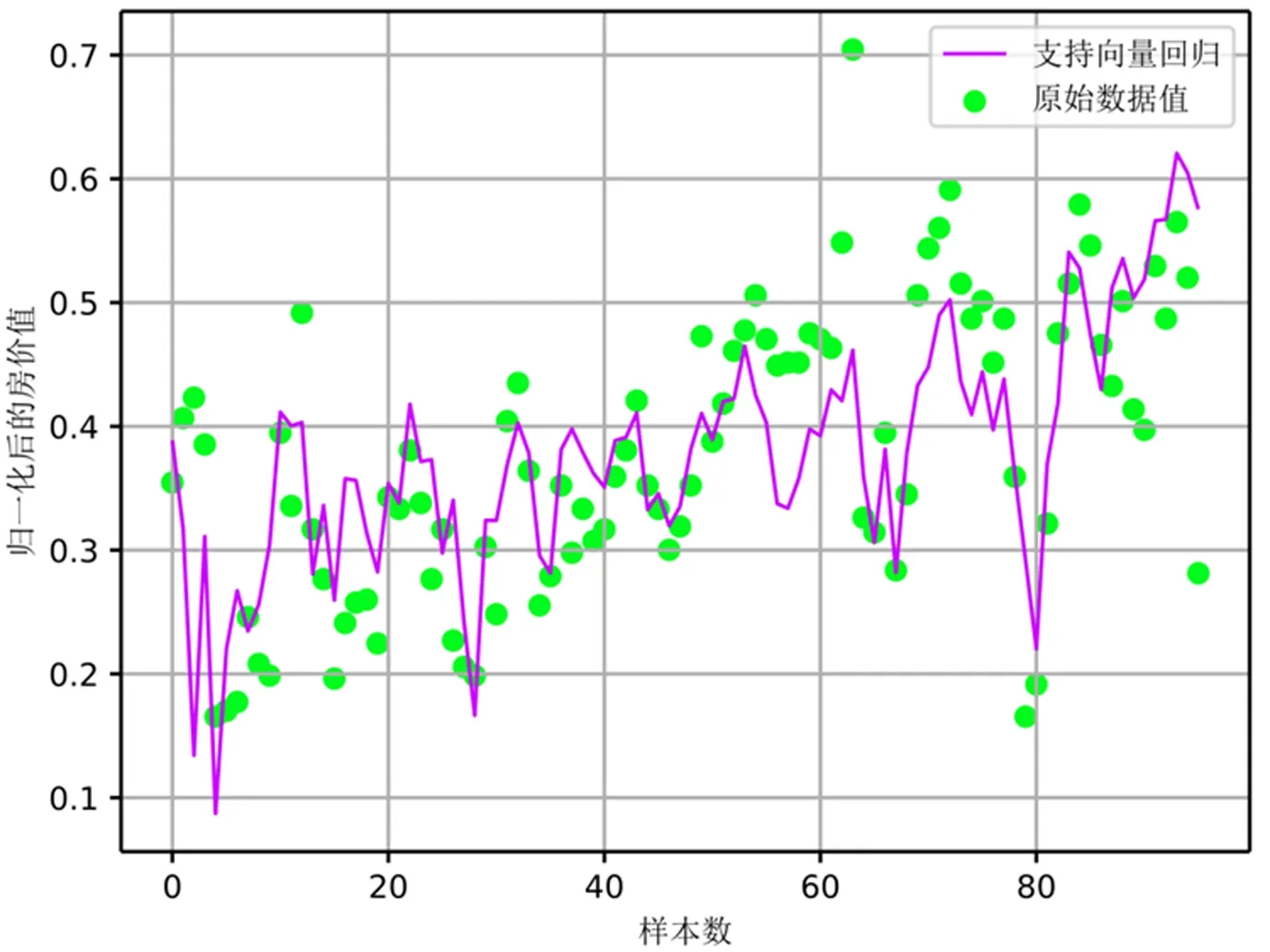
图3 SVR模型与测试数据的拟合图

通过对图3的进一步观察，可以发现实验SVR模型对测试集进行预测时，其预测值的趋势与原始值基本保持一致，误差相对较小。同样除了图像的观察，也需要用真实的数据进一步说明。表2即为使用MAE、RMSE、MAPE 3种模型评估算法分别对4种回归模型的预测效果进行评估。

表2 模型测试误差分析表

通过表2的数据分析，SVR模型在MAE、RMSE、MAPE这3项指标中均为最小值，根据其原理可知，其预测效果在4个模型中为最好。而梯度增强回归对未知数据的预测效果表现较差，不适用于房价的预测中。图4为不同模型的EV得分情况。

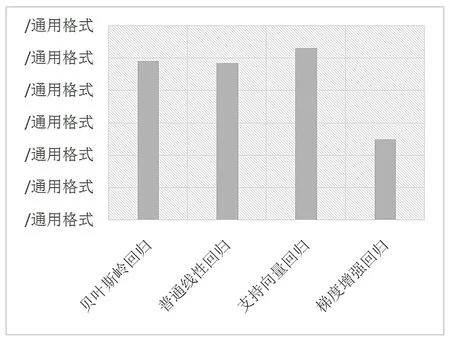
图4 模型测试的EV得分对比图

由图4可知，在波士顿房价数据的预测中，SVR算法训练出的模型准确率达到50%以上，其次为贝叶斯岭回归，普通线性回归也表现出较好的效果。而梯度增强回归在对变化性比较随机的房价数据进行预测时，其效果表现一般。

4结论

SVR算法训练出的模型，对于未知房价数据有较好的预测效果。其预测效果已经达到了50%以上，在实际情况中具有一定的参考价值。该预测模型对于房地产行业以及国家相关部门均具有一定指导意义。