浅谈如何激发学生的问题意识
刘晓君


“疑,思之始,学之端”,思维和学问是从疑问和好奇开始的。有数学家讲过,提出问题是比解决问题更重要的思维活动。可见善于质疑、善于提问是多么的重要。问题意识的强弱可以体现学生思维水平的高低。在教学中,我们常发现成绩较好、能力突出的学生问题意识更强,成绩较差、能力相对弱的学生问题意识也相对较弱。老师们常希望学生们有问题一定要问,但常常发现问问题的少之又少。产生这种现象的原因是什么呢?
首先,从非智力因素的方面来讲,学生普遍存在这样一种心理:老师太严肃,不愿与老师接近;害怕自己所提出的问题太肤浅会招来别人的讥讽;或者害怕自己所提的问题招来老师的不理睬甚至生气,所以不如不问。再加之,老师以及教材的“权威”常常会使学生完全相信他们从而根本没有质疑的意识。
再者,从智力因素的方面来讲,许多学生根本就不会问问题,于有问题处发现不了问题。在传统备课中,老师们考虑更多的是知识目标,学生是否把定理公式学会,一道习题是否把方法讲清楚。但是,在定理公式等知识的探究过程中,在习题的讲解中,是否把核心数学思想体现出来,是否关注学生的深度思维活动,可能没有在教学时给予关注。也就是只注重学生如何解答的训练,而忽略如何思考、如何发问的培养与指导。结果造成学生不善于提问,失去了大部分的想象力和创造力。
老师们经常跟学生说不懂多问,但是我们经常会发现,很多学生不知道问什么?偶尔问个问题,也只是因为某道题不会做。其实要想提出有深度的问题,首先对问题本身要有自己的思考,对问题背后所涉及到的知识要有全面的了解。所以一个有价值的问题的提出,并不是一蹴而就的。
一、运用赏识教育,让学生在数学课堂上有积极期望
一个班级学生的基础往往层次不齐,有的孩子接受能力很快,而有的则很慢。老师提问时,如果学生答不上来,可能会批评或者给予压力。但是,越是批评打击,思维越是打不开,问题更加答不上来,更别说深度思考了。所以,要多运用赏识教育,多鼓励学生,激发他们的兴趣。多宽容,多认同,多赞许,在温情的环境下,在言谈举止中缩短与学生心灵的距离。学生对数学有了兴趣,才能把心理活动指向和集中在学习的对象上,此时学生的感觉和知觉处于活跃状态,注意力高度集中,观察敏锐,思维丰富。才能把自己的困惑讲出来,于有问题时敢于问问题。
二、从生活中的实例出发,感知数学问题的发生过程
常说数学来源于生活,在教学设计时,可以多借助实际问题情境来引入。贴近学生生活,让学生能够较好的感知,从而激发兴趣,引发思考。比如在负数的引入中,教师可以给出收入增加5元和减少5元,然后让同学写出数量。绝大部分同学会发现问题:仅以5元来记是不能区分这两种不同的情况。这时可以激发学生去思考,生活中还有哪些类似的实例呢?相信大多数学生都能够说出来。这样简单的活动,对于刚进入初中的学生来说是很有好处的。激发了学生的兴趣,又为后续学习打下伏笔。又如,在学习“立体图形的展开图”时,可以设计一个实际问题:有一只无盖的正方体纸盒,在底面顶点A处有一只小壁虎,在侧面顶点B处有一只蚊子。请你想一想,帮小壁虎设计一条路线,使得小壁虎尽快吃到蚊子。学生分组讨论,各抒己见,兴趣盎然的开始探索了。在解决问题的过程中必然会碰到困难,而此时“问题意识”也就初步形成。
三、让学生多一些自主探索,给他们创造发问的情景。
在研究“三角形三边关系”时,先给出几组数据:(1)7,8,9(2)1,2,3(3)2,4,5(4)6,4,1。让同学们以此长度为边画三角形,学生会很快发现第(2)组和第(4)组数据不能画出三角形。学生就能比较容易得出不是任意三条线段都可以画一个三角形,并在头脑中思考满足什么条件时可以呢?在研究“直角三角形的判定”时,可以结合数学史故事情境:古埃及人曾经将一根长绳打上等距离的13个结,然后固定第一个结,再用钉固定第四个结和第八个结,最后将第十三个结钉回到第一个结处,这样就能钉成一个直角三角形。然后让同学们照此法做一个直角三角形。于是,问题在情景中诞生了。为什么按照这种方法操作,得到的就是一个直角三角形呢?同学们会以极大的兴趣思考。做到了于无形处有问可问。
当然学生自主能力较弱时,学生速度会很慢,也常发现不了问题的实质,提出的问题抓不住重点,这时候,要多正面激励,多引导思考,只要坚持老师与学生都会获益不浅。
四、在开放性问题中,激发学生的问题意识
开放性问题经常会出现在初中数学教学中,这类问题在条件、结论、或解题策略等方面具有一定的开放性。解决这类问题,首先需要将开放的条件或结论进行补充,使开放性问题得以转化,变成常见的封闭性问题,然后再选择合适的策略进行解答。
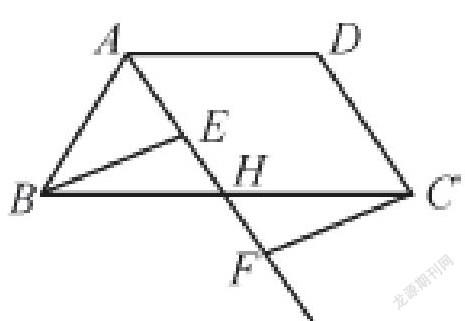
比如:在四边形ABCD中,点H是边BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连接BE,CF.请你添加一个条件,使得△BEH≌△CFH,你添加的条件是____,并证明。
学生在解决这一开放性问题时,首先必须能认真分析已知条件,找出已经具备的全等的条件是什么,才能补充缺的条件。有了这一发现,找出一个正确的结论应该不成问题了。由于问题是开放的,因此,学生可以有不同的答案。在解决问题的过程中,不仅发展了学生的思维,同时培养了学生的问题意识,做到了问我所问。
五、让学生在解题中体验问题意识的重要性,从而增强提问的意识。
对一个问题进行探究时,要能够设计有次第的问题串,助推学生问题意识的萌生。当然,提问是有一定的方法和技巧的,这需要在平时解题时多练习、多总结。下面举两个实例说明一下。
实例一:如图,在平行四边形ABCD中,点E、点F分别是BC和AD上的点,且AE∥CF。说明AE=CF。
这道题并不难,可在实际做时,发现许多学生花了许多时间;有些学生虽做出来了,但方法繁琐。这是为什么呢?有很大一部分原因是不善于观察、提问所造成的。对照图形,应该很敏感的提出这样一个问题:四边形AECF是平行四边形吗?围绕此问题,再结合已知“AE∥CF”,只需寻找“AF∥EC”即可,而这恰恰是题目隐含,问题就迎刃而解。
实例二:如图,在四边形ABCD中,∠BCD=120°,将△ABC绕点A旋转60°,到△ADE,试判断△ACE的形状,并说明理由。
几乎每个学生都可以回答△ACE是等边三角形这一结论。其中的大部分学生在说明理由时,都只是简单的写到“因为AC=AE,∠CAE=60°,所以△ACE是等边三角形。”
这些同学显然没有想到这样一个问题“C、D、E三点在同一条直线上吗”?还有,题目所给的“∠BCD=120°”这一条件是不是没有作用的干扰条件呢?如果能够在心里打下这样的疑问,相信结果一定会不一样的!
可见,具备较强的问题意识确实很重要。由上面的案例二我们也可以看到,解题后应加强反思,这将有利于問题意识的强化。
六、问题解决后进行总结与反思,“问题意识”的升华。
学生在解答一个问题后,常常会转到一个另一个题目上,或者认为没有问题了,如果教师能够抓住问题再设问,会给学生一种“无问之处有新问”的感觉,会促使学生的“问题意识”得到升华。
例如,在小学的时候,学生就知道周长一定的情况下,围一个矩形,正方形的面积最大。进入初中后,会碰到这样的问题:已知围成一个长方形,需要用24米的铁丝,若宽比长少4厘米,求此长方形的面积。学生都会很快解得此题,掌握较好,并认为周长一定情况下只要知道长与宽的关系都可以求解。尽管目的已基本达到,但不妨再问问:宽与长接近时面积的变化情况怎样?学生就会答出:宽与长越接近,长方形面积越大。由此得到一个重要的认识:周长一定的长方形中正方形的面积最大。但是到底为什么呢?激发学生更进一步探究。这样,就可以培养学生追根溯源、勇于探究的问题意识。
总之,培养学生的问题意识,首先要从思想上解放学生,培养学生学习数学的兴趣。同时,还要让学生敢问、会问,在课堂中注意引导,设计各种类型不同的情境,引发学生深度思考的习惯,逐渐让学生善问。使学生逐步学会思考、学会提问。

