高速铁路W1型弹条疲劳性能试验及寿命预测

马薇 伍曾 张景坤 黄新杰

(昆明理工大学建筑工程学院 昆明 650500)

0 引言

扣件系统作为轨道结构重要组成部分之一，利用其弹条的弹性变形所提供的扣压力，将钢轨与轨下结构(包括轨枕、道床板等)联结为一个整体，起到减震缓冲和固定钢轨的作用。而弹条作为实现扣件功能的关键部件，在周期性拉、压、弯曲和扭转的复杂载荷作用下会产生疲劳损伤[1]，甚至疲劳断裂。一旦弹条产生断裂，就会加剧轮轨力，缩减扣件系统寿命，乃至引起重大安全事故。因而，对扣件弹条的疲劳研究势在必行。

针对扣件弹条的疲劳损伤，国内外学者做出了许多研究。但是现有文献大多基于数值模拟和裂纹扩展角度进行研究，对弹条本身的疲劳性能研究较少。故本文从弹条疲劳性能入手，首先对W1型弹条进行静力试验，得到弹条在不同预压力下的应力分布状态，再对弹条施加4种疲劳荷载工况，根据得到的弹条疲劳寿命进行可靠性分析和疲劳寿命预测。

1 W1型弹条静力试验

1.1 静力试验

为了准确得到不同预压力下，弹条的应力分布状态，本文采用了电阻应变测量方法进行静力试验。因为实际服役状态下，弹条疲劳断裂常常发生在后端圆弧处，故在弹条试件上布置5个测点，以测量弹条内、外臂和后端圆弧处的应力值，具体测点布置如图1所示。

图1 弹条各部位名称及测点布置

W1型弹条静力试验在MTS810电液伺服液压试验机上进行，如图2所示。试验从0 kN开始加载至35 kN结束，以2.5 kN为加载梯度，应变电测数据从12.5 kN开始记录，同样以2.5 kN为梯度记录数据至35 kN结束，记录5个测点在0°、45°、90° 3个方向上的线应变ε1、ε2、ε3，根据式(1)可求得测点主应力：

图2 W1型弹条静力试验装置

(1)

式中，σ1，σ2为最大主应力和最小主应力；E为弹性模量，取值1 800 MPa；μ为泊松比，取值0.3。

因为弹条在工作状态下，其应力状态可近似看作两向应力状态，如果用最大切应力理论(第三强度理论)检算弹条强度过于保守，而畸变能理论(第四强度理论)更合理。由式(2)可得到各测点的等效应力：

(2)

1.2 静力试验结果

以MTS810液压机施加的扣压力为横坐标，等效应力为纵坐标，绘制各个测点的荷载-应力图，如图3所示。

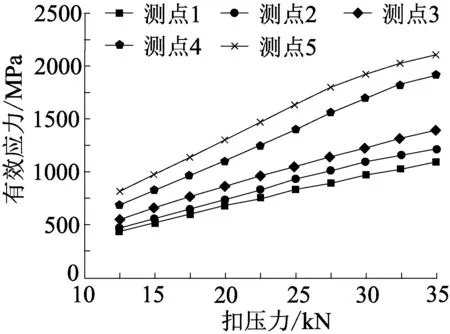
图3 弹条荷载-应力

从图3中可以看出弹条各个测点的应力值变化趋势基本一致，当荷载小于25 kN时，弹条的应力与扣压力呈现出线性增长关系。其中，25 kN时3号测点(弹条内侧圆弧)的应力值最大，为1 632.5 MPa，达到了弹簧钢的屈服强度；而1号测点(弹条外臂)应力值最小，为835.4 MPa。不难看出，弹条在测点3处出现应力集中，并且各测点的应力值自测点3向两侧迅速减小。当荷载大于25 kN时，2、3测点因达到材料的屈服点而产生的局部屈服，故应力增长速度有所下降。在32.5 kN时已经超过了弹条的极限抗拉强度，说明弹条已经开始进入塑性变形阶段。因此，通过试验数据可以确定弹条内侧圆弧是弹条应力最大、最易断裂的位置且弹条的最佳安装预压力为25 kN。

2 W1型弹条疲劳试验

2.1 疲劳试验

W1型弹条疲劳试验同样在MTS810液压试验机上进行，将CFBLZ型压力传感器和D020型位移传感器分别放置在弹条趾端和弹条中端圆弧下方并接入MTS810伺服液压试验机的控制系统采集压力和位置变化的数值。

由上述静力试验可知，扣件弹条合理安装扣压力为25 kN，故以25 kN扣压力作为荷载平衡位置。疲劳试验采用正弦波作为加载波形，频率为5 Hz，疲劳荷载幅值分别为5、7.5、10和12.5 kN，分别对应在测点3，即弹条最大应力值处产生的320、420、540和680 MPa 4个应力幅值。每种循环荷载下取5组试件进行试验，共计20组试件。经过试验，得到W1型弹条在不同应力循环下的疲劳寿命见表1。

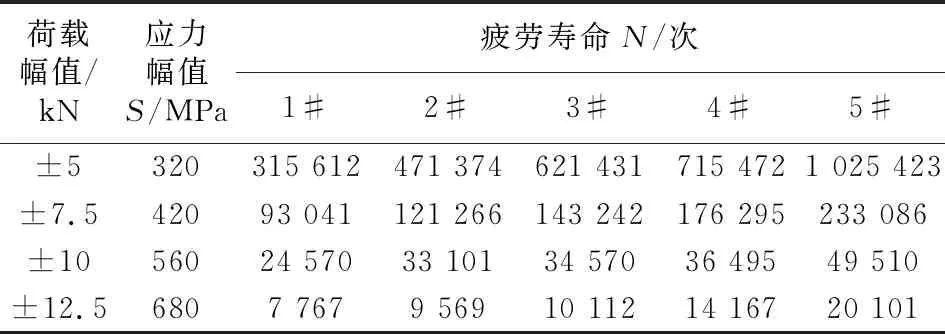
表1 W1型弹条疲劳寿命

2.2 疲劳试验结果分析

2.2.1疲劳寿命的离散性(见图4)

如图4可知，弹条在同一应力循环下的疲劳寿命呈现离散性，而导致疲劳寿命离散的原因有很多，有材料本身的不均匀性、试件加工尺寸差异、试验环境以及试件的原始缺陷。应力水平越低，疲劳寿命越长，离散性就越大。如应力幅值320 MPa下，弹条疲劳寿命从315 612次至1 025 423次，相差3倍以上，故有必要对弹条疲劳寿命进行统计分析。

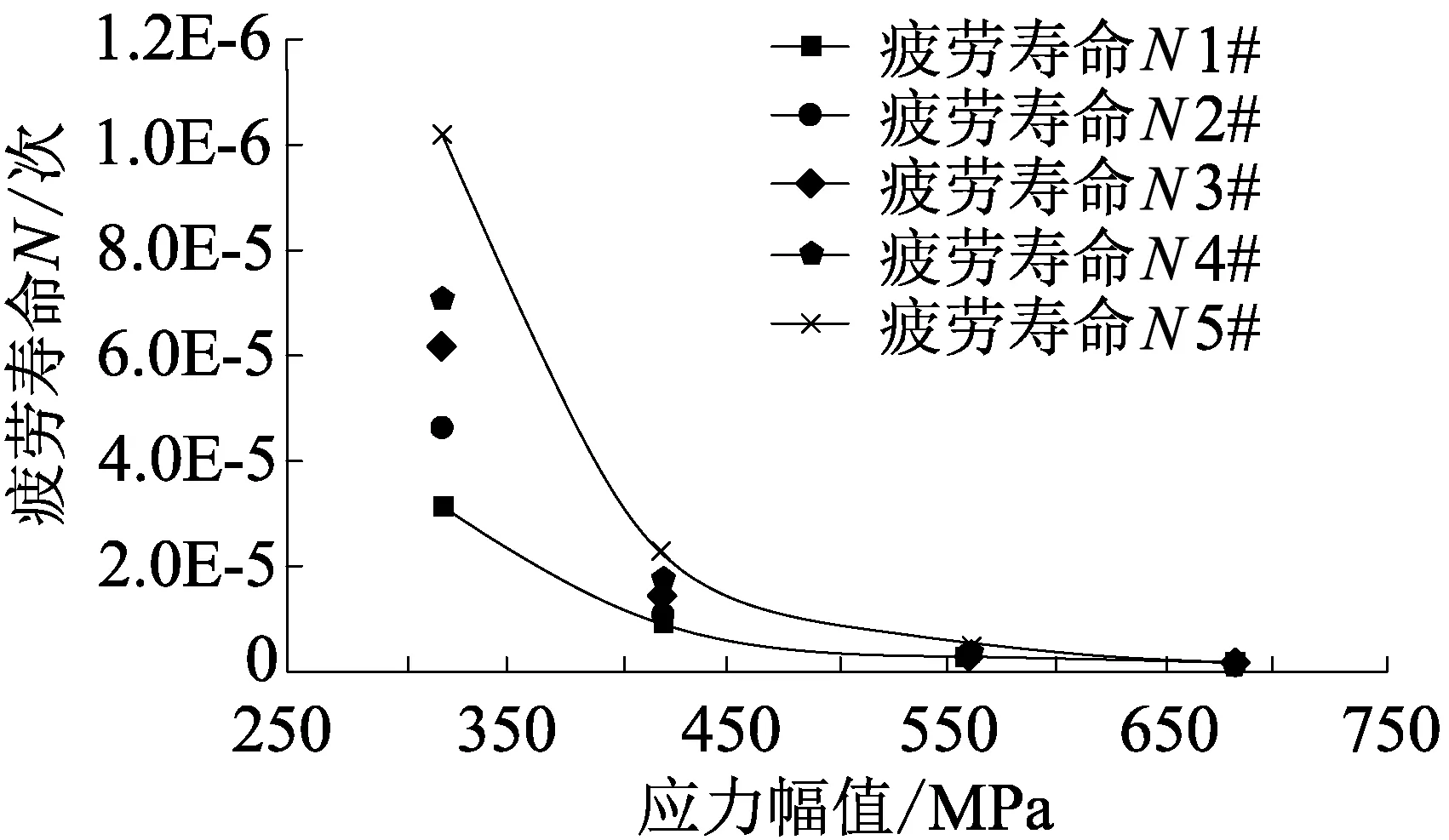
图4 疲劳寿命散点

每一个应力幅值对应5个疲劳试件，属于小子样，可利用正态分布和威布尔分布对其进行统计分析，在此，笔者采用正态分布法。

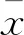
(3)

(4)

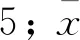
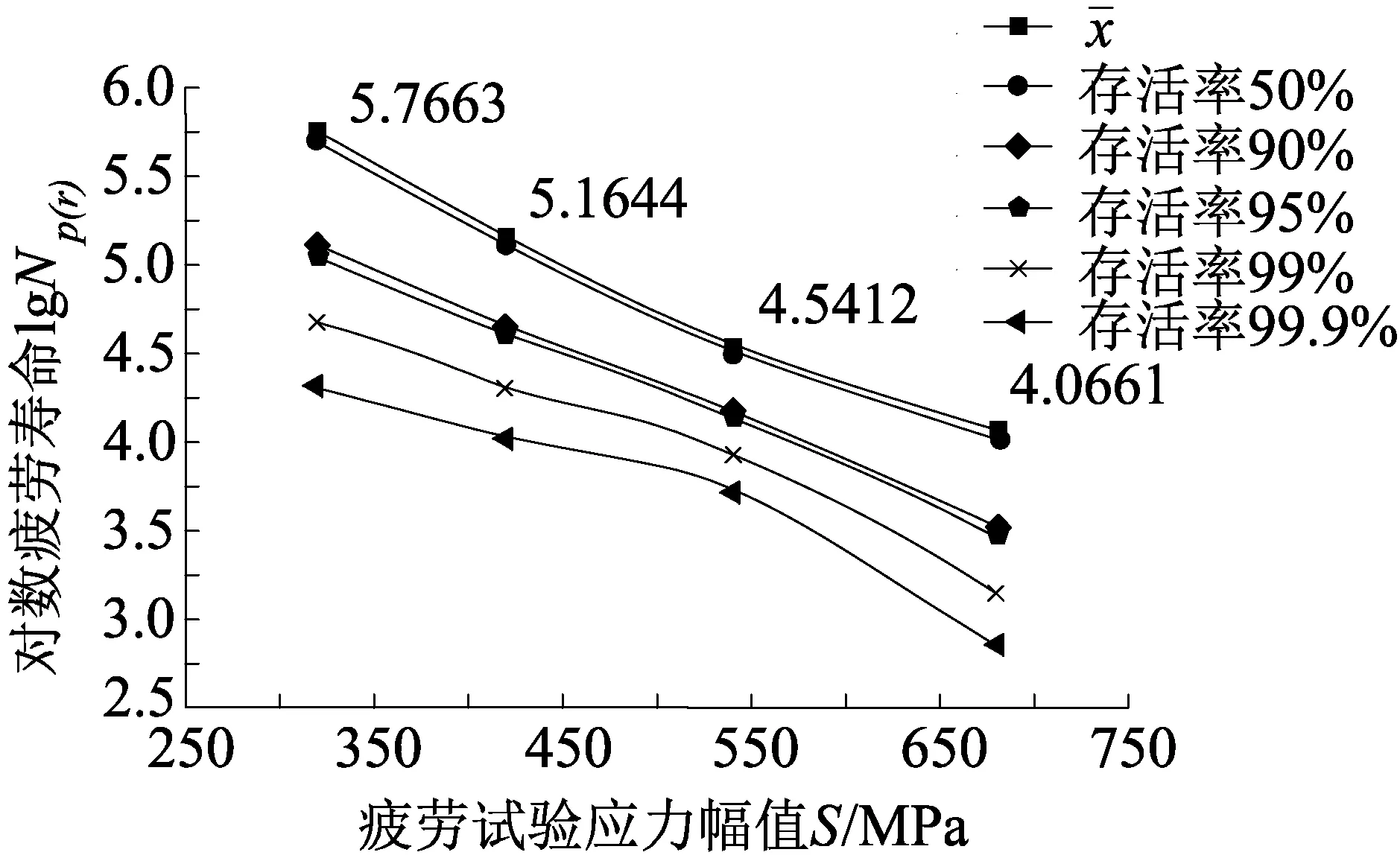
其次，在已知存活率为p,置信水平为r(通常取作90%或95%)的条件下，可由式(5)求得单侧容限系数k，结果列于表2中。最终可根据式(6)求得对应对数疲劳寿命xp(r)。

(5)

(6)

式中，μp和μr分别为存活率p和置信度r对应的标准正态偏量，常用标准正态变量可见表2；xp(r)表示存活率p和置信度r对应的对数疲劳寿命。

表2 标准正态偏量μp及对应单侧容限系数k

2.2.2P-N-S曲线分析

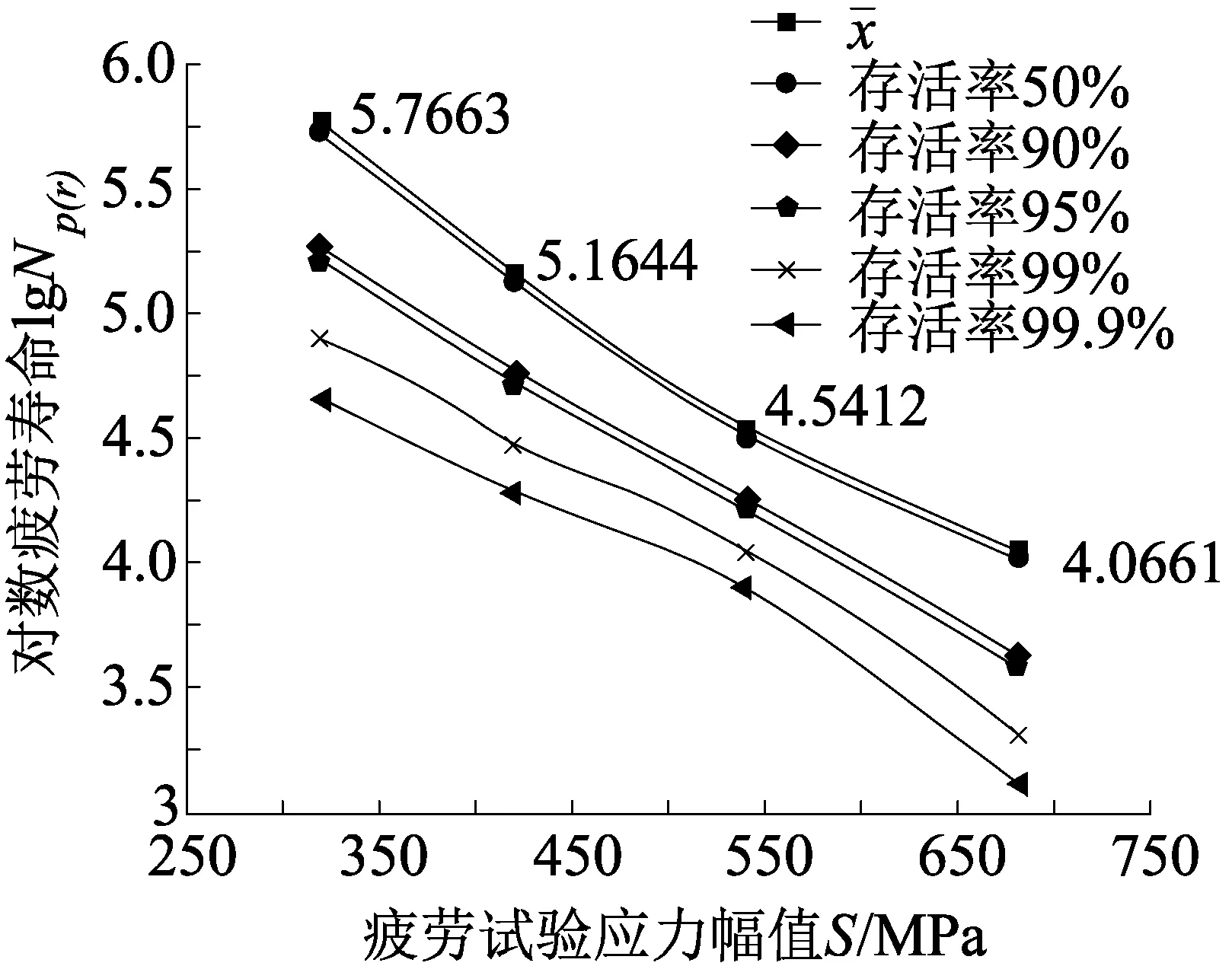
在存活率为p,置信度为r时，求得应力幅值320、420、560、680 MPa所对应的对数疲劳寿命，将数据在以应力幅值S为横坐标，对数疲劳寿命lgNp(r)为纵坐标的系统内进行曲线拟合，得到如图5所示的应力幅值与对数疲劳寿命曲线(P-N-S曲线)。图5的(a)、(b)图分别对应置信度r为90%和95%；图内绘制了存活率p为50%、90%、95%、99%、99.9%和实测对数疲劳寿命共6条曲线。

(a)置信度r=90%

(b)置信度r=95%

不同置信度和不同存活率下的疲劳寿命含义：以应力幅值420 MPa为例，存活率90%，置信度95%，对应疲劳寿命为45 278周次，代表弹条试件在循环应力下作用45 278次，存活率为90%的可靠度有95%。

从图5中可以看出：

(1)应力幅值和存活率不变的条件下，置信度越高，疲劳寿命越小。如应力幅值320 MPa，存活率95%时，置信度90%和95%分别对应的疲劳寿命为163 329周次和115 405周次，疲劳寿命降低近30%左右。

(2)在置信度和应力幅值不变情况下，随着存活率的提高，疲劳寿命锐减。如在应力幅值320 MPa，置信度95%时，存活率由50%提高到99.9%，对应疲劳寿命亦从504 568周次衰减到20 686周次，可见存活率愈高，对疲劳寿命的拟合愈发保守。其他应力幅值下的疲劳寿命变化规律与应力幅值320 MPa基本一致。

(3)置信度和存活率不变条件下，疲劳寿命随着应力幅值的升高而降低，且疲劳寿命衰减程度随之增大。置信度95%，存活率90%时，应力幅值320 MPa、420 MPa、560 MPa、680 MPa 对应疲劳寿命分别为132 853周次、45 278周次、15 085周次、3 343周次，疲劳寿命的下降趋势从65.9%上升到77.8%，可见疲劳寿命与应力幅值成反相关关系。

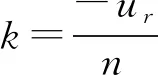
3 疲劳寿命预测

事物间的联系，在数学上通常以变量之间的关系来描述，当相关关系变量X取某定值时，变量Y并无确定的值与之对应，与之对应的是某唯一确定的概率分布及其特征数则称变量Y与X之间有相关关系[2]。在此，利用线性回归方程对弹条的疲劳寿命进行预测。

首先，设定回归方程：X=a+bY。

其次，求解回归系数a,b；可由最小二乘法确定。列如下方程组(式7)：

(7)

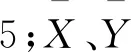
求解可得，回归方程为X=16.260 6-4.201 7Y，取应力幅值50 MPa为梯度，绘制应力幅值由300 MPa增至1 000 MPa的弹条疲劳寿命预测图(图6)，由图6可知，试验数据始终围绕于预测曲线两侧，说明预测趋势与试验数据趋势基本吻合。

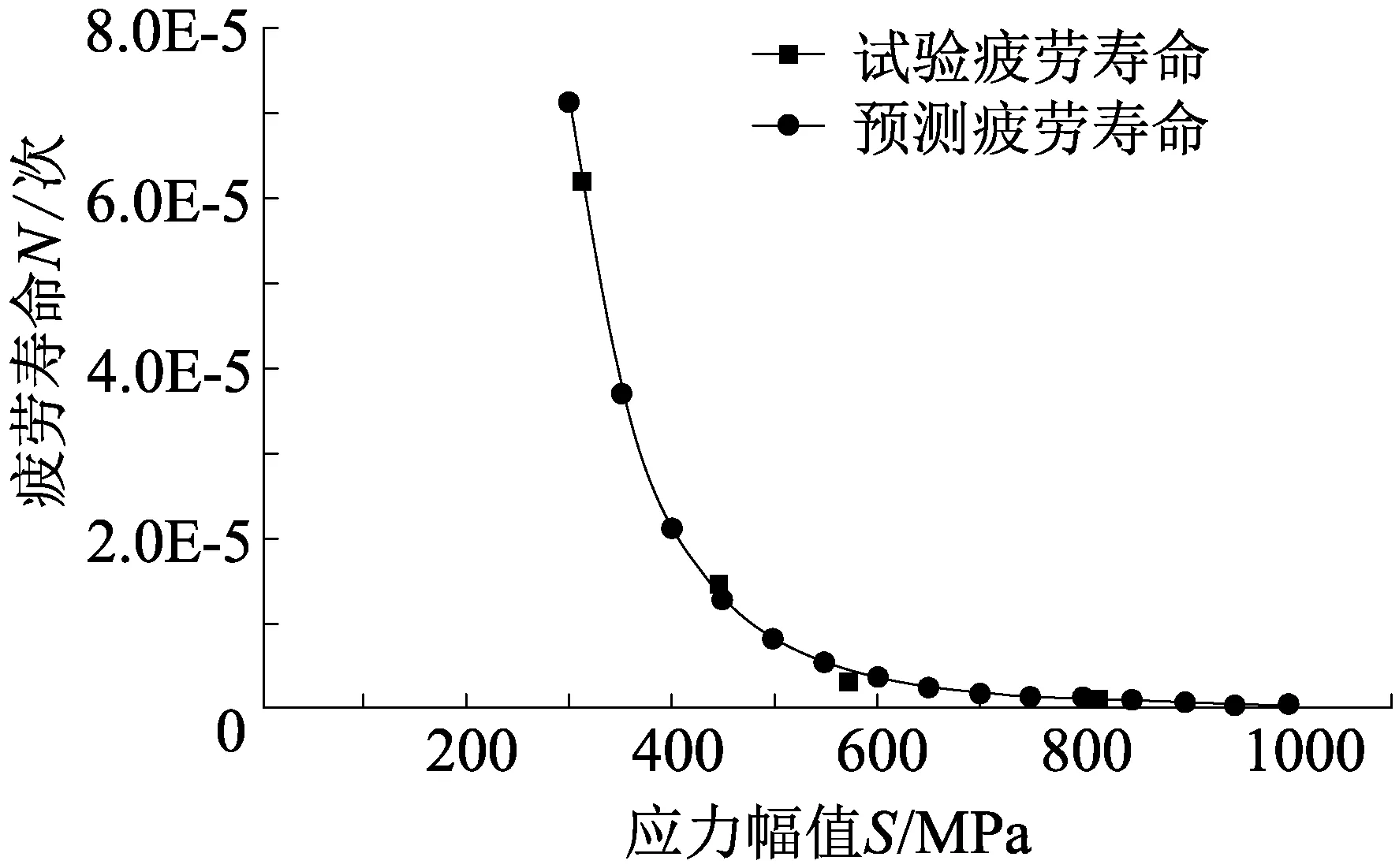
图6 弹条疲劳寿命预测

最后，检验相关关系，由式(8)求得相关系数r=-0.991 9，绝对值非常接近1，说明变量X(对数疲劳寿命)与Y(对数应力幅值)相关密切，由回归方程预测弹条的疲劳寿命较为可行。

(8)

4 结论

通过对弹条进行静力试验和疲劳试验，并且对其疲劳寿命进行分析与预测，可得出以下结论：

(1)扣压力加载至25 kN时，弹条后肢圆弧处出现局部应力屈服，此位置也是弹条常见的疲劳破坏处，同时弹条达到最佳安装位置。

(2)随着疲劳荷载幅值的增加，弹条的疲劳寿命急剧衰减，且疲劳寿命的离散程度也大幅下降。

(3)对弹条疲劳寿命进行正态统计分析，可得出弹条疲劳寿命主要决定于应力幅值，在置信度95%，存活率90%时，随着应力幅值从320 MPa降低到680 MPa，疲劳寿命降低了97%以上，可见疲劳寿命与应力幅值成反相关关系，并且，置信度和存活率越低，拟合疲劳寿命越保守。

(4)通过回归方程对弹条疲劳寿命预测，得到弹条疲劳寿命与应力幅值的关系(X=16.260 6-4.201 7Y)，通过绘图和相关系数的求解，进一步确定了预测寿命的可信度。