春风化雨润心田

杨柳

摘 要：数学学科是一门高度抽象、逻辑严密的自然科学，本身就蕴含了丰富的思想性。数学课堂中的德育应以理服人，要考虑教材的体系和特点，顾及学生的实际情况，注意教育的策略性和可行性，要善于挖掘教材中的德育、情感因素，将数学教学与德育工作有机结合在一起，潜移默化，从而达到“春风化雨润心田”的效果。

关键词：德育;数学教学;案例设计

德育是构建德智体美劳全面培养的教育体系的重要组成部分，在落实立德树人，培育时代新人中发挥着举足轻重的作用，德育一体化建设是落实国家教育战略，培养全面发展的人的重要基础。《普通高中数学课程标准》明确指出：数学教育承载着落实立德树人的根本任务，发展素质教育的功能。在平常的教学中，我们要紧密结合数学学科教学内容，使德育与智育、体育、美育等有机融合，从而实现全科育人的目的。下面，我就以“两点间的距离”为例，来说一下我是如何进行德育一体化设计的。

一、借助适当的情境创设，激发学生的学习热情，培养他们爱学习、爱科学的兴趣

数学学科虽然不像文科知识那样生动活泼，富有情趣，但只要我们抓住数学学科的特点，创设好的学习情境，也能激发学生的学习兴趣，达到渗透德育的目的。

以课堂引入这个环节为例，我们可以采用灵活多样的情境引入，来唤起学生学习的热情。考虑到上一章我们刚刚学过立体几何的有关距离，而下一节学生又将接触到点到直线的距离，所以本节课我采用了知识情境引入，从而帮助学生构建有关距离问题的完整知识体系。

师：说到距离，在我们数学中有很多种，你知道都有哪些？

师：在这么多距离中，哪种距离是最简单的距离？

（此处教师稍微停顿，让学生思考，然后学生回答，教师再进行归纳总结即可。）

师：点到点的距离是最简单、也是最重要的一种距离，因为其他所有的距离都可以转化为点到点的距离来解决。这节课我们就来学习这种最简单也是最重要的距离。

这样的情境引入，是根据数学知识之间的联系、发展与变化来创设的。它让学生明白了这节课的基础性和重要性，培养了学生爱学习、爱科学的兴趣。

二、借助数学知识和思想方法，培养辩证唯物主义世界观

较其他学科而言，数学无论是知识，还是思想方法，都蕴含着极其丰富的辩证法思想，这也是数学学科的一大特点。比如：待定系数法反映了已知与未知的矛盾转化过程，反证法、补集方法是否定之否定规律的体现;数列、指、对函数等教学内容反映了认识事物从特殊到一般的认知规律。下面以推导两点间的距离公式这一环节为例，来进行说明：

[问题1]数轴上两点间的距离公式是什么？

[问题2]如果在直角坐标系中，在x轴上有两点P1（x1，0）和P2（x2，0），那么点P1和P2之间的距离为多少？如果P1P2平行于x轴呢？

[问题3]在y轴上有两点P1（0，y1）和P2（0，y2），那么点P1和P2之间的距离为多少？如果P1P2平行于y轴呢？

[问题4]已知x轴上一点P1（x0，0）和y轴上一点P2（0，y0），那么点P1和P2之间的距离为多少？

[问题5]已知平面上任意两点P1（x1，y1）和P2（x2，y2），那么点P1和P2之间的距离又为多少？

师：勾股定理是数学中解决度量问题最重要的一种方法，除了两点间距离的推导，后面将要接触的点到直线的距离，圆的弦长和切线长，以及空间直角坐标系中的距离问题，都会用到勾股定理来推导。

（此处是为了向学生渗透应用勾股定理的意识，让学生体会勾股定理的文化价值，激发学生的民族自豪感。）

[问题6]你能说出数轴上两点间距离公式和平面上两点间距离公式的联系和区别吗？

[问题7]你能试着大胆猜测空间中两点间的距离公式吗？

（这个探究体现了“未知到已知”“由特殊到一般”“数与形”的相互对立与统一，让学生学习用辩证的观点来分析解决问题。）

总之，在教学中，适时地、恰当地渗透辩证唯物主义思想教育，不仅有利于学生对数学知识的深刻理解和对数学方法的熟练掌握，更有助于学生形成良好的思维品质和科学的世界观。

三、利用数学的学科特点，培养学生善于思考、勇于創新的科学精神

数学中的很多问题都具有相似性和可迁移性。所以，在日常教学中，我喜欢通过一组组变式训练，引导学生揭示数学问题的本质，帮助学生构建系统的知识体系。比如：在本节课中，我没有简单地“就题论题”，而是对例题进行变式训练，这样能使学生更深刻理解两点间的距离公式，培养学生的探索精神和创新能力。

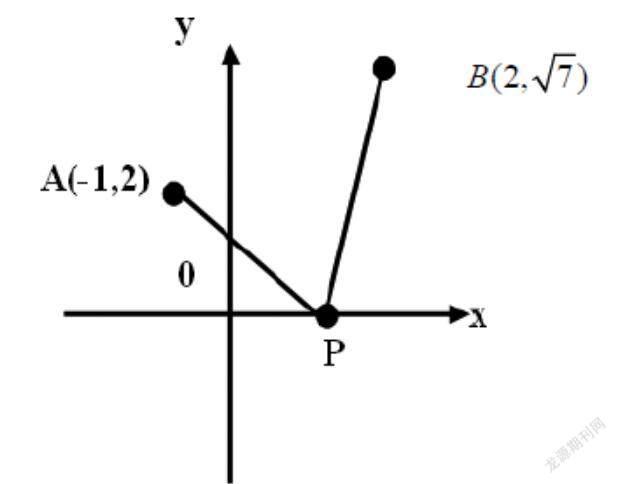
[例1]已知点，在x轴上求一点P，使，并求|PA|的值。

[变式1]如果在y轴上呢？

[变式2]如果在直线y=2x+3上呢？

[变式3]已知点，若，求点P的坐标满足的方程。

[变式4]在x轴上求一点P，使得|PA|+|PB|取最小值。

（例题和前两个变式是对在平面直角坐标系中，求点的坐标这一类问题的研究;变式3属于求轨迹方程问题，为后面学习求曲线方程做好铺垫;变式4是属于利用对称知识求最值问题。这组变式通过不断变换例题的条件，引深拓展，使一个题目延伸出三类问题，唤起了学生的好奇心和求知欲，培养了思维的创新性。）

数学教育家波利亚曾形象地指出：“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找找，很可能附近就有好几个。”恰当合理的变式训练，不仅能产生触类旁通、举一反三的学习效果，而且有利于培养学生的应变能力，开阔学生的思路，培养学生的创新能力，形成“以不变应万变”的能力，从而终生受用！

四、借助探索重难点知识和了解数学史，培养学生严谨认真、勇于挑战困难的优秀品质

（一）探索重难点知识

人的一生总会遇到困难和挫折，对困难和挫折的承受能力是立足于当今复杂多变世界的必备能力。因此，培养学生遇到困难，勇于克服和顽强拼搏是很有必要的。对于难度较大的数学题目，学生在解决过程中，如果不具备坚定的信心、顽强的毅力，是很难解决的。本节课的難点是利用坐标法来证明几何问题，因此我借助这组探究题，来培养学生知难而上的优秀品质。

[探究]证明：矩形四条边的平方和等于两条对角线的平方和。

师：本题能不能利用初中学过的几何法来进行证明？

师：能不能利用坐标法来证明？

（此处的矩形因为两条相邻的边互相垂直，所以学生无论是建系，还是设点，都能很快解决，教师也及时给予肯定与鼓励，培养了学生学习数学的信心。）

师：如果要证明平行四边形四条边的平方和等于两条对角线的平方和呢？能不能利用初中学过的几何法来进行证明？

师：能不能利用坐标法来证明？如果可以的话，如何建系？如何设点？

建系是本节课的难点。为了突破难点，在这里要求小组合作解决，并在讨论完后，小组选派代表展示他们的建系方法。让学生自己对比、分析得出哪些系建的比较恰当，哪些系建的不易得出点的坐标，进而总结出建系的原则与标准。通过展示对比建系的方法，让走弯路的同学明白自己思维的障碍点，从挫折中磨炼其意志品质，培养其勇于挑战困难的意志与勇气。

（二）了解数学史

众所周知，每个数学概念和公式背后都有着它的故事：或许源于一个灵感;或许是几代人甚至是几个世纪人的共同努力使之完善的过程。这种“一次次建立概念、一次次推翻概念、一次次修正概念、一次次完善概念”的艰辛过程，正是教育学生面对困难与挫折，严谨认真、顽强拼搏的最好素材。在本节课最后，我还向学生介绍了笛卡尔建立坐标系的一个有趣传说：

在笛卡尔之前，几何是几何，代数是代数，它们各自为政，互不相扰。但是，传统的几何过分依赖图形和形式演绎，而代数又过分受法则和公式的限制，这一切都制约了数学的发展。笛卡尔一直期待着找到一种方法，架起沟通代数与几何的桥梁。一天，他生病卧床，又想起了这个折磨他很久的问题。天花板上，一只蜘蛛吐丝结网，忙个不停。要结一张网，蜘蛛该走多少路啊！他先把蜘蛛看成一个点，那么这个点离墙角有多远呢？离墙的两边多远？昏昏沉沉的，他思考着，计算着，不知过了多少时间，笛卡尔突然感觉茅塞顿开：要是知道蜘蛛和两墙之间的距离关系，不就能确定蜘蛛的位置吗？确定了位置后，自然就能算出蜘蛛走的距离了。于是，他郑重地写下了一个定理：在互相垂直的两条直线下，一个点可以用到这两条直线的距离，也就是两个数来表示，这个点的位置就被确定了。就这样，笛卡尔建立了直角坐标系。它第一次用数形结合的方式将代数与几何联系了起来。

通过学习，让同学们感受到：笛卡尔的坚忍不拔和锲而不舍的探索精神，为学生树立了学习的榜样。这段史料很好的培养了学生在学习的路上不畏艰难、勇于进取、艰苦奋斗的奉献精神！

总之，对于数学课堂的德育渗透，有很多的教育契机和切入点。只要善于捕捉好的教育素材，并考虑好学生的思想实际和知识的接受能力，因势利导，循序点化，就一定能达到“春风化雨润心田”的效果！

参考文献

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[S].北京：人民教育出版社，2020.

[2]鲁基教.山东省中小学德育课程一体化实施指导纲要[S]，2016.

[3]何艺妍.德育教育在数学教学中的渗透[J].中学教学参考，2011（29）.