带式输送机永磁驱动系统自抗扰同步控制策略*

郝建伟， 鲍久圣， 葛世荣， 胡而已， 杨小林， 阴 妍

[1.中国矿业大学 机电工程学院，江苏 徐州 221116；2.中国矿业大学(北京) 机电与信息工程学院,北京 100083；3.北京百正创源科技有限公司，北京 100081]

0 引 言

煤矿智能化是煤炭工业高质量发展的核心技术支撑。加快煤矿智能化发展，是中国煤炭工业高质量发展的战略任务和必由之路[1]。带式输送机作为煤矿井下主要的煤炭运输设备，正朝着重型化、智能化的方向发展[2]。当今带式输送机多采用交流异步电机配合减速器、液力耦合器等中间传动装置进行驱动，存在效率低、起动不平稳、重载起动困难等问题，制约着带式输送机驱动系统的智能化发展。永磁同步电机(PMSM)工作原理不同于异步电机，具有低转速、大转矩、功率因数高等特性，可直接驱动带式输送机，无需中间传动装置，提高了系统的传动效率和可靠性，便于实现智能化控制[3]。

当前，在传统PID调速控制策略的基础上，国内外研究学者又提出了许多先进的PMSM调速控制策略，例如：Klinlaor等[4]提出了一种抗饱和的PI控制策略调节PMSM的转子转速，减小了电机起动转矩的超调量和反应时间；杨永乐等[5]针对PMSM调速系统易受电机参数负载扰动变化影响的问题，提出了基于负载观测的滑模变结构的PMSM矢量调速控制，提高了系统反应速度和鲁棒性；孙玉良等[6]在传统矢量控制的基础上引入了模型参考自适应控制算法，实现了PID控制器中参数的动态调节，降低了系统的控制误差；王福杰[7]对比分析了模糊PID控制和BP神经网络PID控制的PMSM调速方案，得出了神经网络PID控制抗扰动优于模糊PID控制，而在实时性方面模糊PID控制更有优势的结论。

在带式输送机的多电机驱动系统中，多电机同时工作易出现电机间不同步运转现象[8]，甚至造成电机损坏。针对该现象国内外研究人员提出了不同的多电机同步控制策略，例如：蒋毅[9]将模糊理论与虚拟主轴控制结构相结合，优化了系统同步性能；Zhang等[10]将模型预测控制与相邻耦合控制结构结合，提出了基于串级预测控制的速度同步控制方法，提高了系统的抗干扰能力和同步性能等。

目前国内外的研究重点多针对于高速小功率PMSM，对矿用低速大功率PMSM研究相对较少。模糊控制、模型参考自适应控制和人工智能控制算法多与PID控制算法相结合，可以实现PID控制器中参数的动态调节，但是其需要对建立的模型进行大量训练以此获得精确的参数调整规则，实现过程较复杂，也受限于PID控制算法自身原理的缺陷，难以达到较优异的控制性能；滑模变结构控制摆脱了传统PID控制算法的限制，但在进行控制律切换时存在抖振问题，降低了控制精度等。因此，基于当前带式输送机多PMSM调速控制策略、同步控制策略研究的不足和自抗扰控制(ADRC)在抗干扰能力、调节速度上的显著优势，本文提出了基于ADRC的带式输送机多永磁电机驱动系统同步控制策略，通过在MATLAB/Simulink中对比仿真分析，验证其能有效提高带式输送机多电机驱动系统的抗干扰能力、控制精度和同步性能。

1 PMSM自抗扰调速控制策略

为了解决传统PMSM调速控制策略中PID控制器的缺陷，韩京清[11]于20世纪末提出了ADRC的概念和结构原理。如图1所示，ADRC主要由跟踪微分器(TD)、扩张状态观测器(ESO)和非线性反馈控制律(NLSEF)3部分组成。

图1 ADRC结构原理图

传统的非线性自抗扰控制(NLADRC)设计和调参较复杂，故本文将基于线性自抗扰控制(LADRC)并以id=0矢量控制为基础设计2种不同的PMSM自抗扰调速控制策略。

1.1 一阶ADRC控制器设计

图2为一阶LADRC控制器调速控制策略，将传统矢量双闭环控制中的转速环PID控制器替换成一阶LADRC控制器，电流环仍采用PID控制器实现对电机的矢量调速控制，其设计过程如下。

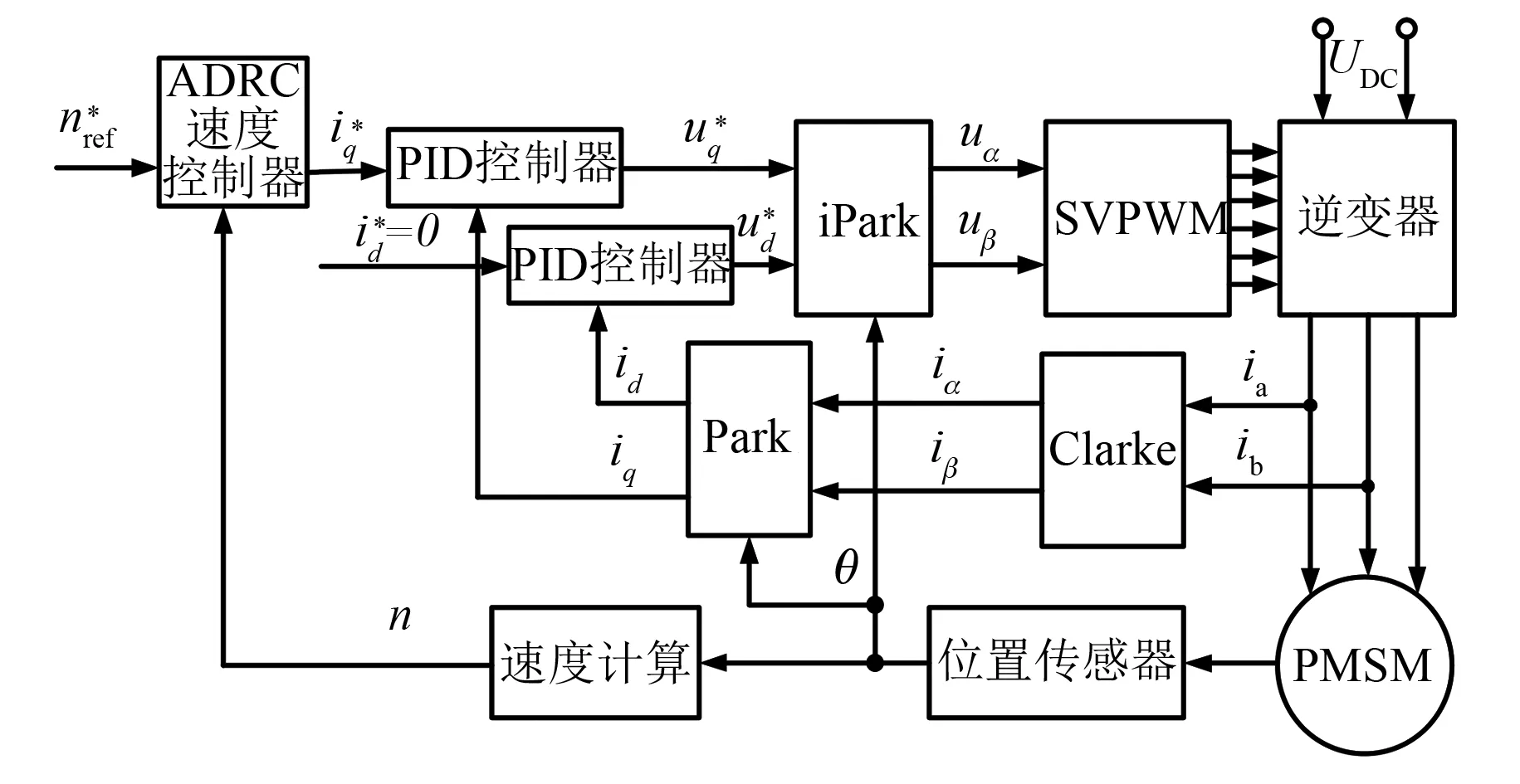
图2 一阶LADRC调速控制策略框图

由PMSM机械运动方程可知：

(1)

式中：ωm为电机机械角速度；TL为电机负载转矩；p、J、φf、B分别为电机极对数、转动惯量、定子磁链和阻尼系数；iq为电机q轴分量电流。

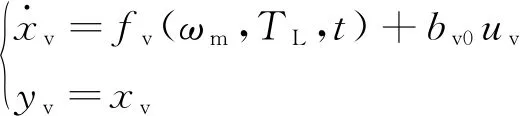
(2)

由于转速环控制不需要生成转速的微分信号，故省略TD。结合上述设计速度环LADRC控制器的ESO和NLSEF为

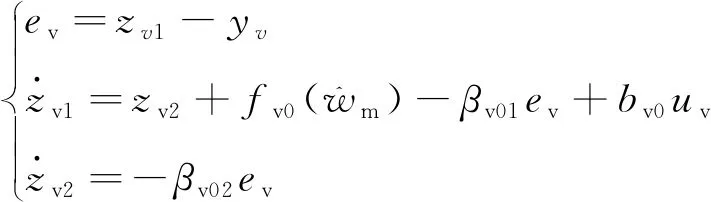
(3)

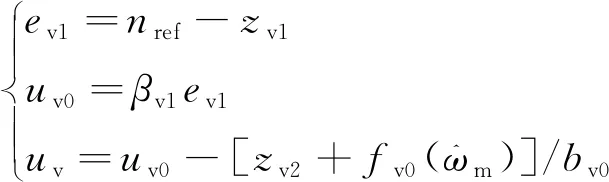
(4)

式中：zv1为转速观测信号；zv2为转速中未知干扰的观测信号；nref为电机给定转速；βv1、βv01、βv02为待定系数；uv为一阶LADRC控制信号；δv为线性段的区间长度，取0.01。

电流环采用PI控制器即可满足要求，其设计较简单，本文不做过多阐述，其控制器参数为Kpd=Kpq=20，Kid=Kiq=150。

1.2 二阶ADRC控制器设计

由于ADRC具有处理高阶被控对象的特性，所以提出第2种基于LADRC控制器的调速控制策略。如图3所示，将速度控制器和q轴电流控制器整合成二阶LADRC控制器，其设计过程如下。

图3 二阶LADRC调速控制策略框图

对式(1)求导后并化简得：

(5)

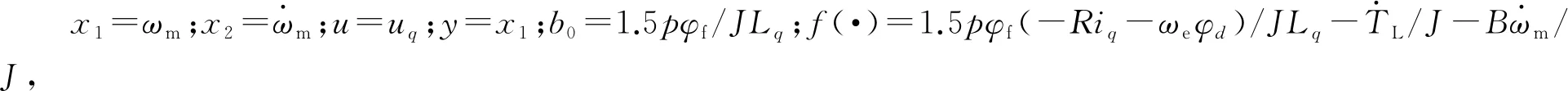
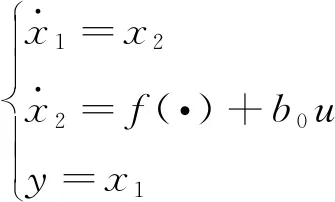
(6)

设计二阶速度-电流环LADRC控制器TD为

(7)

式中:v1为转速的跟踪信号；v2为转速跟踪信号的微分信号；fh为最速控制综合函数，其具体推导过程可参考文献[11],其数学公式为

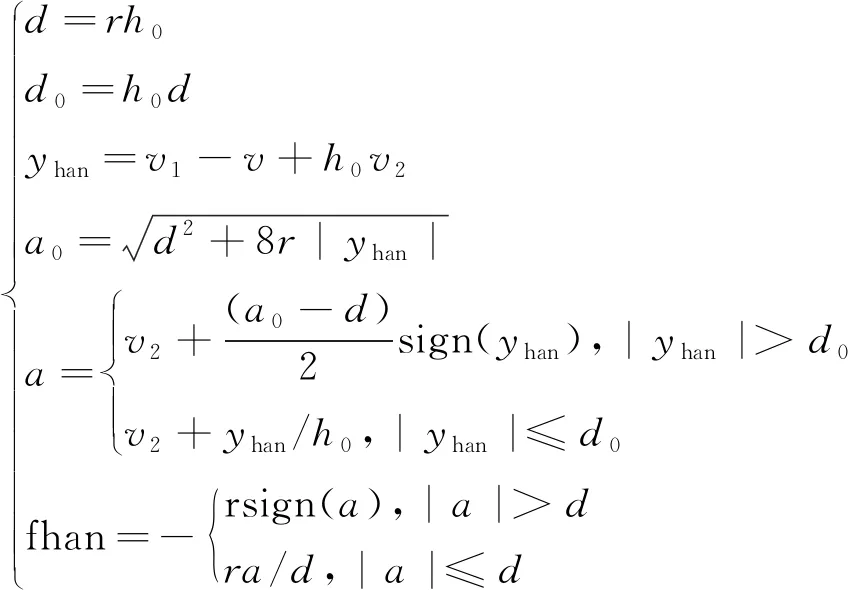
(8)

式中:r为决定跟踪速度的速度因子；h0为TD的滤波因子，取0.01；sign(·)为符号函数。

设计二阶速度-电流环LADRC控制器的ESO和NLSEF分别为

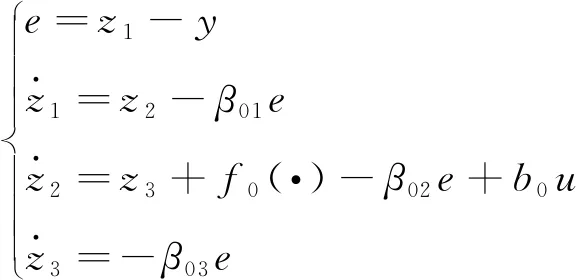
(9)

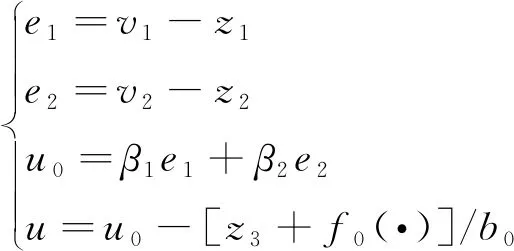
(10)

式中：β01、β02、β03、β1、β2为待定系数；z1和z2分别是v1和v2的观测信号；z3为未知干扰的观测信号；u为二阶LADRC控制信号。

1.3 PMSM调速控制策略仿真

选定某品牌大功率PMSM为研究对象，开展仿真对比分析，具体参数如表1所示。

表1 PMSM参数

在MATLAB/Simulink中搭建基于LADRC控制器矢量调速控制模型，如图4所示。

图4 LADRC控制器矢量控制模型图

表2 一阶LADRC控制器参数

表3 二阶LADRC控制器参数

为了比较3种不同控制策略性能的优劣，在3种不同运转工况下进行了电机仿真试验对比。

1.3.1 电机空载运转工况

带式输送机电机空载运转阶段仅需承受输送带的自重，故设空载运转工况下所受负载转矩为5 000 N·m，其生成转速、转矩曲线如图5、图6所示。

图5 空载工况下电机的输出速度曲线

图6 空载工况下电机的输出电磁转矩曲线

由图5、6看出，空载工况下基于PI控制器和一阶LADRC控制器的电机在起动时超调量较大，需要较长时间才能达到额定转速，而二阶LADRC控制器的电机几乎无超调，在0.1 s就达到了额定转速，并且基于二阶LADRC控制器的电机输出转速和电磁转矩的整体波动均更小。电机起动时由于给定的速度信号是阶跃起动信号，会导致电机输入电流过大，而实际电机很难能承受过大电流，所以带式输送机驱动电机应采用软起动的方式，由于本文仅对控制策略性能进行比较验证，在此对其起动方式不做过多阐述。

1.3.2 电机满载运转工况

当带式输送机由于各种故障导致停机而再次起动时，电机往往处于满负载的工况下，设其满载工况的负载转矩为电机的额定负载转矩50 935 N·m，其生成转速、转矩曲线如图7、图8所示。

图7 满载工况下电机的输出速度曲线

图8 满载工况下电机的输出电磁转矩曲线

从图7、图8可知，满载工况下3种控制器均能较快地使电机达到稳定运转状态，基于PI控制器的电机转速达到稳定前有一定波动，基于一阶LADRC控制器的电机转速超调量最小，但是其输出电磁转矩波动较大，基于二阶LADRC控制器的电机转速有轻微超调，达到稳定运转时间较快，运转期间输出电磁转矩波动最小。

1.3.3 电机处于变负载运转工况

表4中，设置带式输送机遵循由空载—轻载—重载—停机的变负载运行工况，其生成的速度、转矩曲线，如图9、图10所示。

表4 电机变负载仿真工况

图9 变负载工况下电机的输出速度曲线

图10 变负载工况下电机的输出电磁转矩曲线

由图9、图10可知，基于PI控制的电机转速超调量较大，受到负载冲击时调节时间较长，电机输出电磁转矩波动较大；基于一阶LADRC控制的电机受到负载冲击时反应时间较快，但在起始时电机转速存在超调，且在运转期间输出电磁转矩波动也较大；基于二阶LADRC控制的电机在极短时间内几乎无超调的达到额定转速，运转期间输出电磁转矩波动较小，受到负载冲击时调节时间最短。

综上所述，基于二阶LADRC控制器的控制策略具有更好的控制性能，因此本文将基于二阶LADRC控制器开展带式输送机多永磁直驱系统同步控制策略研究。

2 带式输送机多永磁电机驱动系统同步控制策略

多永磁电机驱动带式输送机运转时由于存在机械安装和制造误差、落煤量差异等问题，易造成电机间转速不同步现象。传统偏差耦合同步结构虽然结构简单，但其速度补偿器为固定增益，仅考虑了转动惯量对各电机同步性能的影响[14]。因此本文基于模糊PI速度补偿器提出了改进型偏差耦合同步控制结构(图11)，其模糊PI速度补偿器数学表达式为

图11 改进型偏差耦合控制结构

(11)

2.1 模糊PI补偿器设计

模糊PI补偿器设计主要包括输入输出变量模糊化、建立模糊规则、模糊逻辑推理、解模糊化4个过程[15]。

输入输出变量模糊化。确定电机转速差e和转速差变化率ec的物理论域分别为[-2，2]和[-500，500]，ΔKp和ΔKi物理论域分别为[-10，10]和[-50，50],其中PI速度补偿器初始值设为Kp=20，Ki=150。为了便于分析与计算本文选择将输入e、ec和输出ΔKp、ΔKi的物理论域统一量化到 [-6，6]集合区间，将输入e、ec和输出ΔKp、ΔKi的物理量化论域集合均变换成模糊语言集合： {NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)}，并确定如图12所示的隶属度曲线。

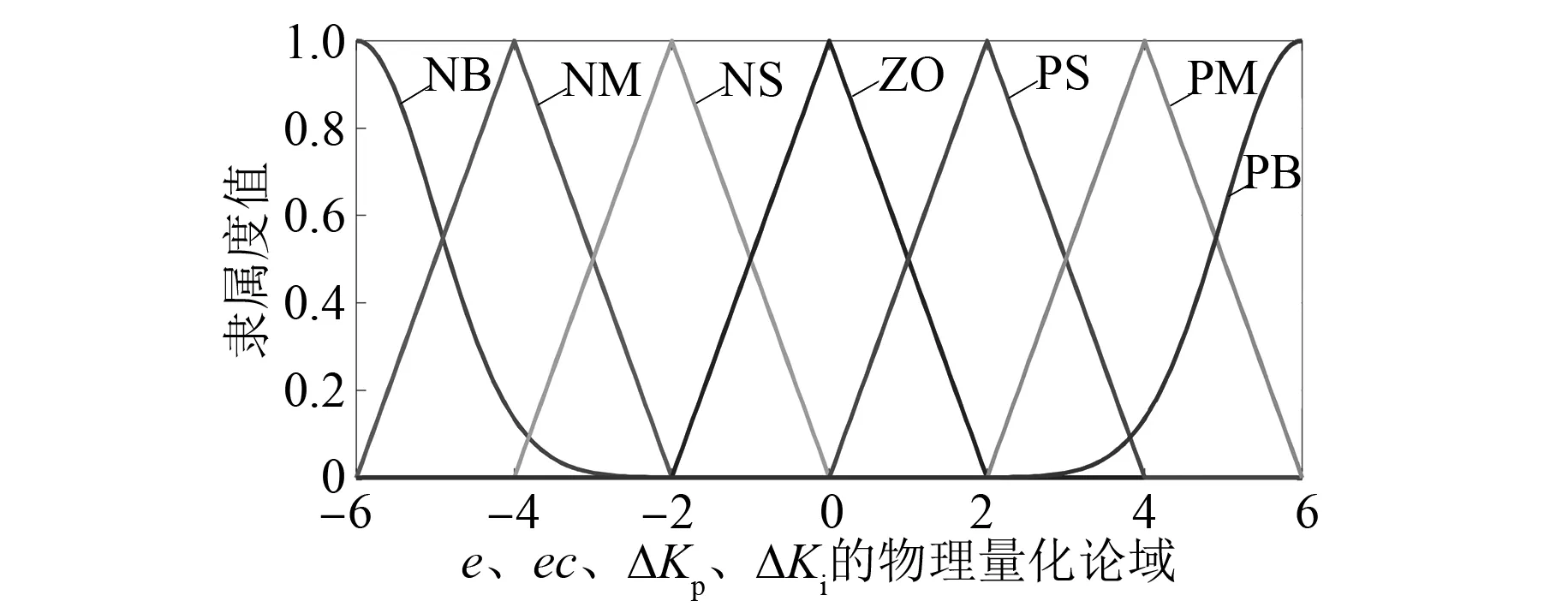
图12 e、ec、ΔKp、ΔKi的隶属度曲线

模糊规则和逻辑推理。依据长期实践的总结和专家经验，建立如下模糊规则[16]：

(1) 当转速误差e为PB、NB时，若转速误差变化率ec为NS、PS或者ZO时，应当在保证无超调的情况下尽量增大Kp；

(2) 当转速误差变化率ec为PB、NB时，若e很小，应减小Kp和Ki，反之应当增大Kp和Ki；

(3) 当误差e和ec同号时，说明转速误差朝着增大的方向发展，应该同时增大Kp和Ki；当误差e和ec异号时，说明转速误差朝着减小的方向发展，应当减小Kp和Ki。

依据上述3条模糊规则建立ΔKp和ΔKi的模糊控制决策表如表5、表6所示。由于模糊控制中的解模糊化的常用方法固定，在Simulink中的Fuzzy Logic Controller模块中自带解模糊化过程，故这里针对解模糊化过程不做设计。

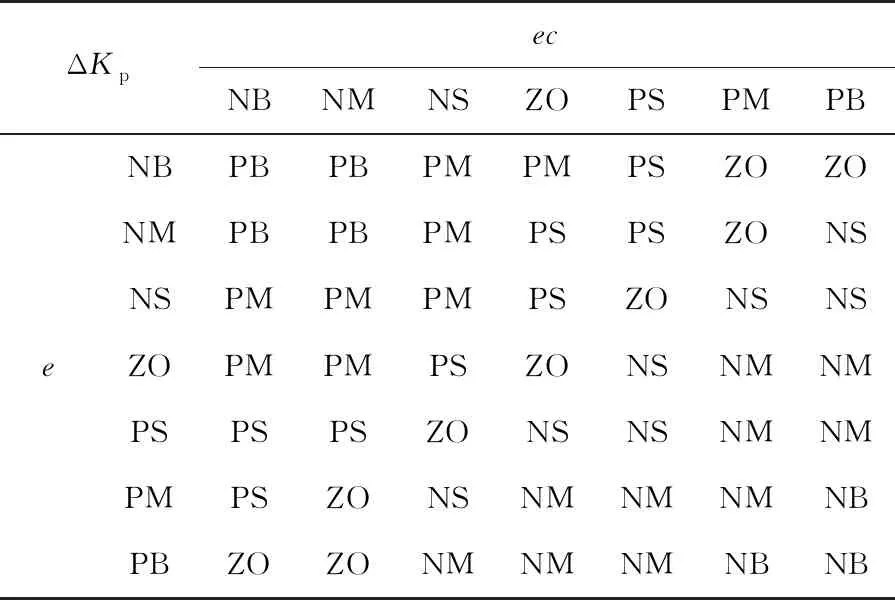
表5 ΔKp的模糊控制决策表

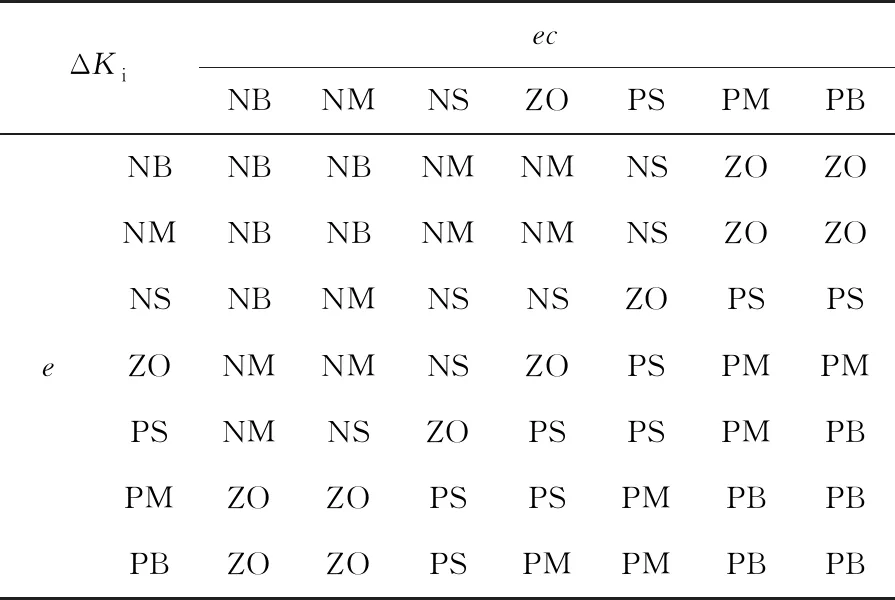
表6 ΔKi的模糊控制决策表

2.2 带式输送机永磁驱动系统同步控制仿真

为了验证改进型偏差耦合同步控制策略的同步性能，开展主从、传统偏差耦合和改进型偏差耦合控制结构的同步控制仿真对比。3台电机(电机参数相同)仿真工况仍遵循空载-轻载-重载-停机进行研究，如图13所示，其输出转速、电机同步误差、电磁转矩曲线如图14～图16所示。试验电机分别命名为电机1、电机2、电机3。

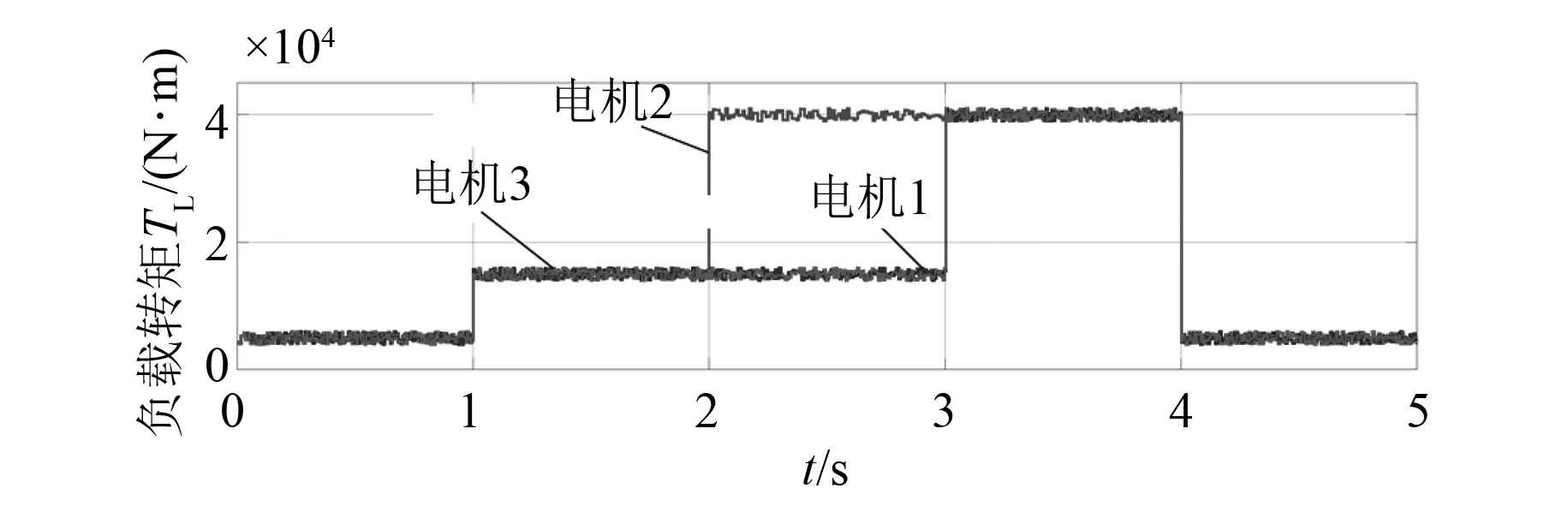
图13 多PMSM仿真工况

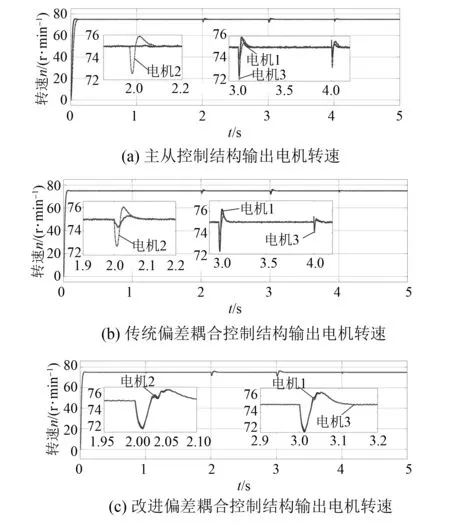
图14 3种控制结构输出转速

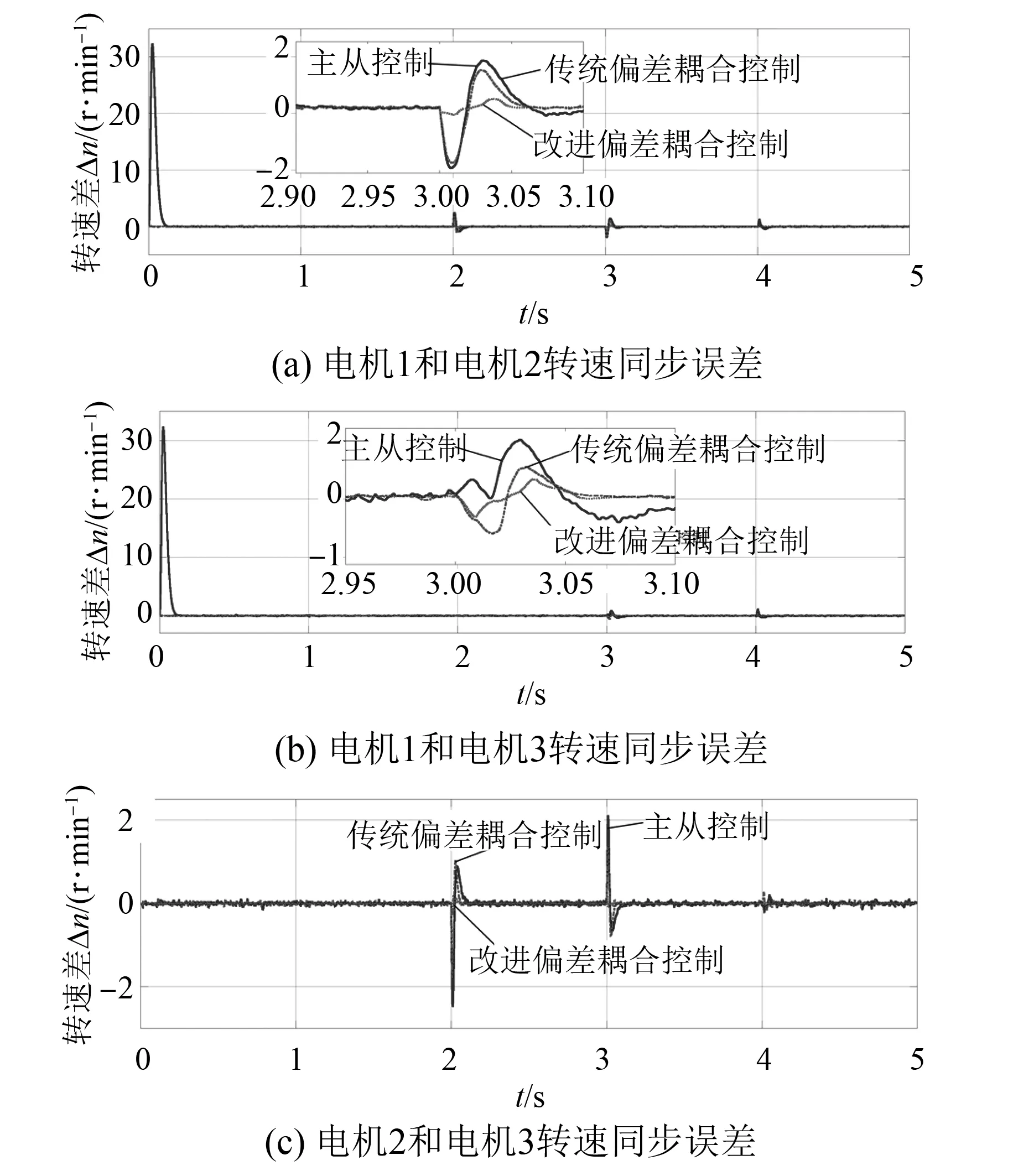
图15 3种控制结构电机间同步误差

图16 3种控制结构输出电磁转矩

由图14对比可以看出，电机在起始时响应速度均较快，当电机2在第2 s受到的较大负载冲击时，主从控制结构中电机2的转速下降接近3 r/min，电机1和电机3转速不发生变化，导致在第2 s时主从控制结构中电机间存在较大的转速差；传统偏差耦合控制结构中电机2转速的变化引起了电机1和电机3的同步变化，但是其同步变化速度跟不上电机2转速的下降速度，故电机2与另外2台电机间也存在较大转速差；改进型偏差耦合控制结构通过动态调整PID速度补偿器中的参数，使电机在转动过程中电机间转速误差始终保持在较小的范围内，因此在改进型偏差耦合控制结构中3台电机仅存在较小的转速误差。由图15也可以看出，主从控制结构电机间同步性较差，最大转速差达33 r/min；传统偏差耦合控制同步性次之，最大转速差接近2 r/min，而改进型偏差耦合控制同步性最好，最大转速差低于0.5 r/min。在实际运行过程中电机达到平稳运转的前提是其输出的电磁转矩等于输入的负载转矩，当电机输出电磁转矩增大的瞬时其速度会瞬间下降，反之速度会瞬间上升。从图16对比分析可知，在第1 s 3台电机同时受到接近的负载转矩冲击时，3种控制结构中电机的输出电磁转矩变化趋势无明显差异；在第2 s电机2受到较大冲击后，主从控制结构中电机1和电机3的输出电磁转矩无变化，而偏差耦合同步控制结构中电机无主从之分，传统偏差耦合控制结构中电机2的负载转矩变化引起了电机2的输出电磁转矩的变化，电机2输出电磁转矩瞬间增加引起了电机1和电机3输出电磁转矩瞬间的微小跟随变化，但是其瞬时增加趋势较小，而改进型偏差耦合控制结构中电机1和电机3输出电磁转矩瞬时增加趋势较大，该趋势的大小会直接体现在电机间的转速中；在第3 s时，电机1和电机3负载转矩突变时，改进型偏差耦合控制结构在极短的时间内3台电机的输出电磁转矩就几乎达到相同。综上所述，改进型偏差耦合控制结构具有更好的同步性能。

3 结 语

本文基于ADRC技术、偏差耦合控制结构、模糊PID控制算法，提出了基于ADRC的带式输送机多永磁电机驱动系统同步控制策略，开展了相应的仿真对比试验，得出如下结论：

(1) 基于二阶ADRC控制器的大功率PMSM双闭环矢量控制策略具有更好的跟踪性能、响应速度和控制精度，解决了大功率PMSM抗干扰能力弱、非线性强和调节时间慢的弊端。

(2) 基于模糊PID速度补偿器的改进型偏差耦合控制结构进行多永磁电机同步控制时，实现了PID速度补偿器中参数的动态自调整，电机间具有较好的同步性能和稳定性，减少了由于不同步现象带来的电机损耗，延长了电机的使用寿命。

(3) 本文设计的控制策略虽然存在ADRC控制器难调参、仿真工况与实际工况有差别和缺乏物理试验等弊端，但是总体而言其对提高带式输送机多永磁电机驱动系统同步控制性能具有重要的研究价值和意义。