基于Sum of Squares分解技术的电力系统鲁棒综合控制方法*
陈明媛, 王 钧, 周智成, 谢代钰, 潘连荣
[1.广西电网公司电力调度控制中心,广西 南宁 530012;2.华蓝设计(集团)有限公司,广西 南宁 530011]
0 引 言
随着快速电液式调速系统的发展,原动机调速控制在改善电力系统稳定性方面发挥着越来越重要的作用。因此,将发电机组的励磁控制和原动机控制有机地结合起来,实现综合控制,成为发电机控制发展富有潜力的探索方向[1-3]。文献[4]引入多指标线性控制设计方法来研究发电机组的综合控制问题。该方法既能使系统获得良好的动态性能,也能获得满意的静态性能。文献[5]应用目标全息反馈法来处理发电机组的非线性综合控制问题。该方法可将非线性控制系统的多个控制目标均约束在性能指标中,从而实现系统的多目标控制。
在文献[4-5]中,所建的发电机组模型均未考虑系统参数的不确定性及干扰的影响。基于建模时忽视不确定性数学模型的非线性控制方法并不能够充分发挥其作用。要提高非线性控制设计方法的有效性,使设计所得的控制律在实际应用中得到满意的控制效果,在系统建模和控制器设计过程中考虑不确定性对系统的影响是非常有必要的。
针对电力系统在不确定参数下的控制问题,基于控制理论[6]、耗散理论[7]、自适应控制理论[8]等的非线性鲁棒控制方法被提了出来。王宝华等[9]运用反步递归法来设计包含不确定参数的发电机综合控制规律;兰海等[10]通过递推法构造保证电力系统对于外部干扰具有增益抑制性能的存储函数,从而得到实现干扰抑制和稳定的系统控制规律。在这些方法中,随着递归推导步数的增加,控制规律的设计过程也会越来越繁杂。Okou等[11]应用自适应控制方法设计电力系统的鲁棒综合控制规律,该方法针对系统的每一个不确定项,均设计一个动态估计环节以应对其影响,然而这些动态估计环节会大大增加控制器的复杂程度。
文献[12]中提出了一种基于Sum of Suqares (SOS)分解技术的鲁棒控制方法(SOSRCA)。该方法无需对不确定参数设计状态估计器,也无需繁琐的递归设计构造出对干扰具有增益抑制性能的系统存储函数,因此简化了设计过程并且降低了控制规律的复杂程度。本文将SOSRCA应用于充分考虑不确定参数及干扰的发电机鲁棒综合控制模型中,在李雅普诺夫稳定理论下,可用一组状态相关不等式来保证包含不确定参数的多机电力系统是鲁棒稳定的,并且该系统对于外部干扰具有L2增益抑制性能。通过SOS分解技术的半定规划松弛算法可对该不等式组进行求解得到系统的鲁棒综合控制规律。最后,将得出的控制规律应用于三机电力系统模型,通过仿真证明了SOSRCA所获得的控制规律不仅对于不确定参数具有鲁棒性,还对干扰具有良好的抑制能力,能够有效地提高电力系统的暂态稳定性。
1 多机电力系统的鲁棒综合控制问题
1.1 多机电力系统鲁棒综合控制的数学模型
考虑一个具有n台汽轮发电机的多机电力系统,第i台发电机的鲁棒综合控制数学模型[13],转子运动方程和电磁动力学方程如下:

(1)
其中,
Pei=E′qiIqi
(2)

(3)
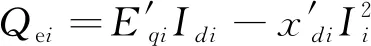
(4)

将方程式(1)写成紧缩的仿射非线性方程形式:
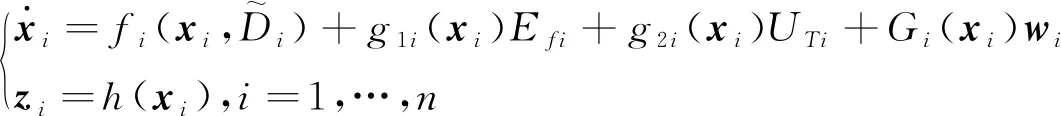
(5)
其中,

(6)

(7)
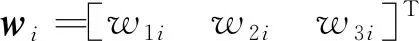
(8)

(9)

(10)


(11)

1.2 包含不确定参数的多机电力系统的鲁棒稳定性与L2增益抑制性能分析

在鲁棒控制理论中[14],定义系统的L2增益为
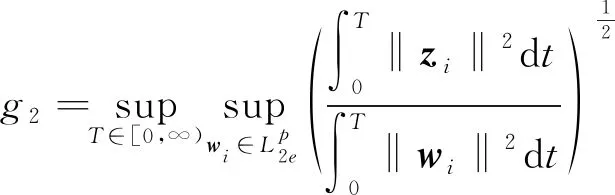
(12)
式中:sup为上确界;‖zi‖和‖wi‖分别为输出向量zi和输入向量wi的欧几里得范数。
那么输入对输出的影响得以量化,第2个控制目标中的干扰抑制问题可描述为L2增益抑制问题。


(13)
将系统式(5)重写成:

(14)

以下定理给出能令系统式(14)是鲁棒稳定的,并且具有L2增益抑制性能的条件:


(15)
那么系统式(14)是鲁棒稳定的,并且具有L2增益抑制性能,即当wi=0时,原点是渐近稳定的;当wi≠0时,该系统由扰动输入wi到输出zi的L2增益不大于给定的正数γi。
证明:
(1) 鲁棒稳定性。将wi=0代入不等式(15)中,可得:

(16)
然后将式(16)从时间0到T进行积分,得
Vi(xi0)-Vi(xiT)≥
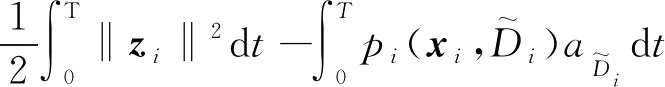
(17)

(18)
Vi(xi0)-Vi(xiT)≥0
(19)
余下的证明类似于李雅普诺夫稳定理论的证明,请参考文献[16],这里不再赘述。
(2)L2增益抑制性能[17]。将式(15)从时间0到T进行积分可得:

(20)

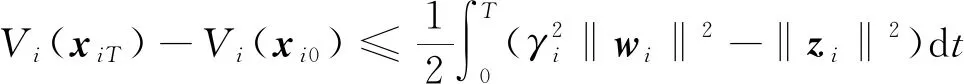
(21)
又根据条件Vi(xi0)=0及Vi(xi)≥0,可以得出:

(22)
由L2增益的定义可知,干扰输入wi对于系统的输出zi的影响小于γi。
1.3 多机电力系统的鲁棒综合控制规律设计理论
在定理1的鲁棒稳定性及L2增益抑制性能的分析中,若李雅普诺夫函数Vi(xi)与控制规律Efi、UTi均是未知的情况下,求解不等式(15)是非凸的,非凸问题目前很难得出其有效解。为了能有效地求出系统式(14)的鲁棒综合控制规律,其李雅普诺夫函数选取经典形式:

(23)


(24)

选取:
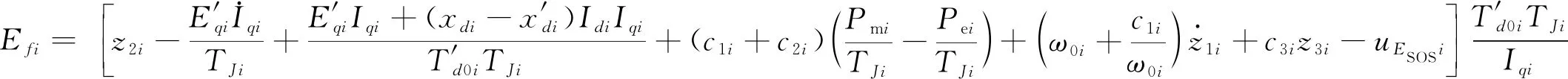
(25)
UTi=TV∑i(-c4iz4i+uUSOSi)+Pmi
(26)
将式(25)和式(26)代入式(24),可得:

(27)
式中:uESOSi、uUSOSi、c1i、c2i、c3i和c4i均为待定的多项式。
通过观察式(27),可知c1i与c2i具有乘积关系,即二者之间的关系是非线性。这种非线性关系不利于问题的有效求解,因此,将c1i设定为一个给定的正常数,那么其余所有的未知量对于式(27)均是凸的。
根据定理1,下面给出系统式(14)的鲁棒综合控制设计方法(RCCA)。
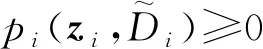

(28)

(29)
c2i≥0,c3i≥0,c4i≥0
(30)
那么系统式(14)是鲁棒稳定的,并且具有L2增益抑制性能。
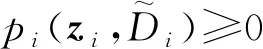
2 基于SOS分解技术的鲁棒综合控制方法
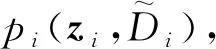
2.1 SOS多项式分解技术
若存在多项式f1(x),…,fm(x),使得如下式子成立:

(31)
那么多项式p(x)是一个SOS多项式。很显然,对于所有x∈Rn,p(x)是SOS多项式自然意味着p(x)大于或等于零。
对于条件式(31),可作如下等价,存在一个半正定的矩阵Q使得如下式子成立:
p(x)=zT(x)Qz(x)
(32)
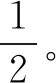
2.2 基于SOS分解技术的鲁棒综合控制设计方法
根据1.3节中给出的鲁棒综合控制的设计方法,将式(28)~式(30)中的正定条件,用SOS条件来替换,那么可得出基于SOS分解技术的鲁棒综合控制方法(SOSCCS)。


(33)

(34)
c2i、c3i和c4i均是SOS多项式
(35)
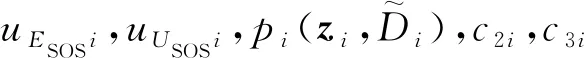
2.3 SOSTOOLS鲁棒综合控制规律的求解过程
(1)初始化程序。
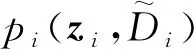

(4)定义目标方程为式(33)~式(35)。
(5)调用SOSTOOLS工具箱的多项式求解器。
将(6)中的结果代入式(25)和式(26)中,得到多机电力系统的鲁棒综合控制规律。
3 系统仿真与结果
上述基于SOS的鲁棒综合控制方法的有效性将在如图1所示的三机电力系统中进行验证。图1中还给出了该电力系统的初始潮流数据。
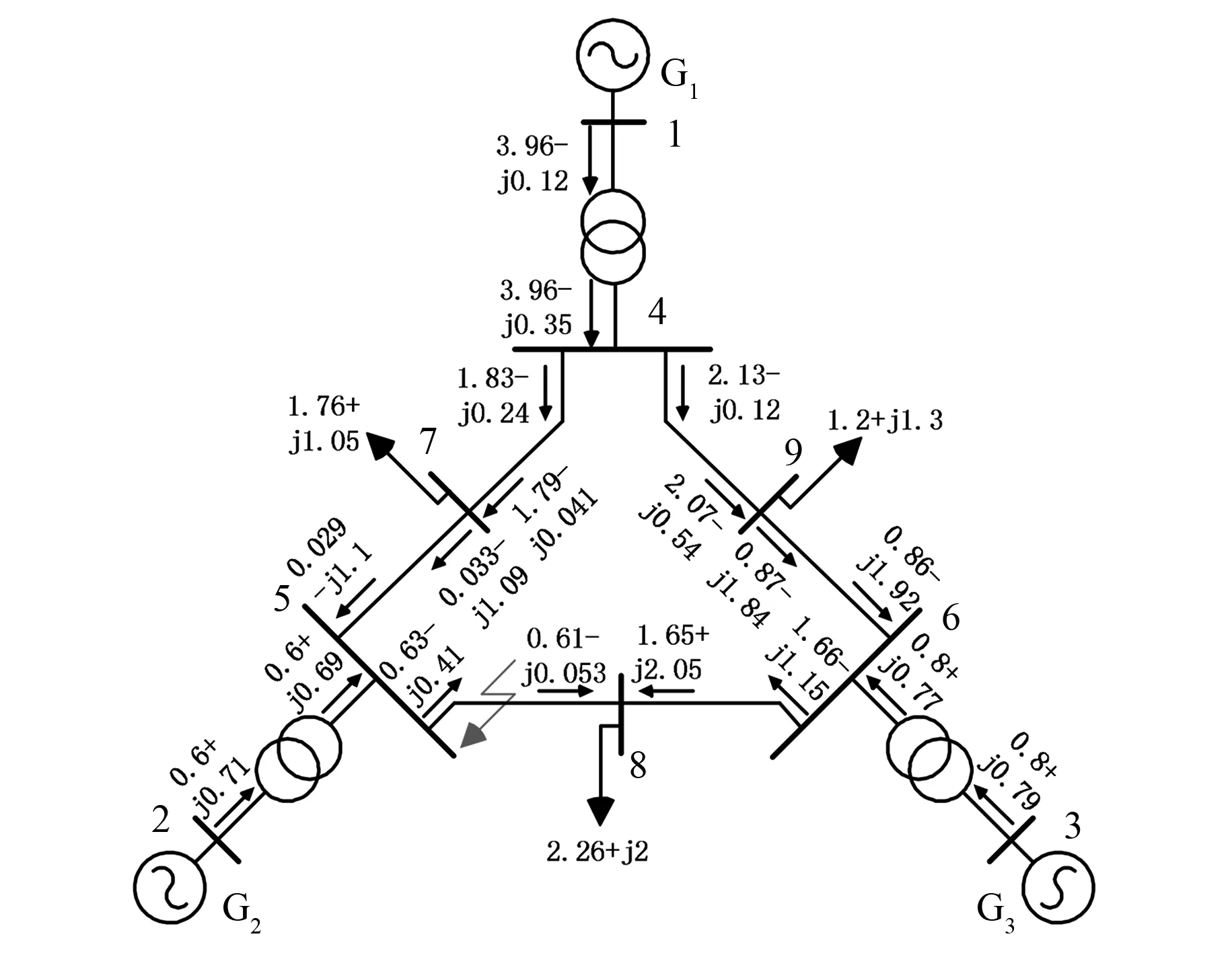
图1 三机电力系统模型及其初始潮流数据
图1中发电机G1是无穷大系统。G2和G3装配有综合控制器,其模型参数如表1所示。

表1 发电机G2和G3的模型参数
3.1 系统不确定参数的范围

表2 不确定参数的上下界
3.2 基于SOS的鲁棒综合控制规律
将c1i和γi取为如下的值:

(36)
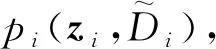
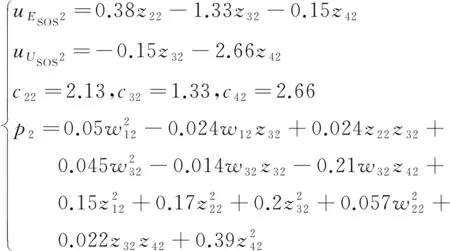
(37)
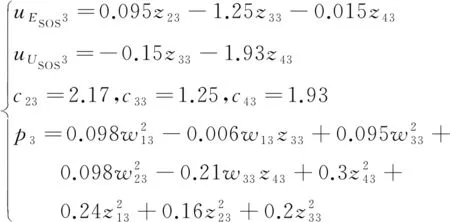
(38)
为验证式(37)和式(38)能使条件式(33)和式(34)成立,将式(36)~式(38)代入式(33)及式(34),用SOSTOOLS工具箱对式(33)和式(34)进行平方和分解:
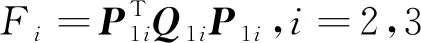
(39)

(40)
其中,
P2i=[z4iz3iz2iz1i]
(42)
Q12和Q13为16×16的矩阵,其特征值如下所示:
Q22和Q23为4×4的矩阵,其特征值如下所示:
eig(Q22)=[2.05 0.61 0.78 1.52]
(45)
eig(Q23)=[2.18 0.82 0.38 1.21]
(46)
显然,矩阵Q12,Q13,Q22和Q23均为正定。
应用定理1,可推出以下结论:

(2)系统式(21)的扰动输入wi到输出zi的L2增益不大于给定的正数γi=0.1。
将式(36)~式(38)中的uESOSi,uUSOSi,c1i,c2i,c3i和c4i的计算结果分别代入式(25)和式(26),便可得到系统的鲁棒综合控制规律:
UT2=(-5.32z42-0.15z32)TV∑2+Pm2
(47)
UT3=(-3.86z43-0.15z33)TV∑3+Pm3
(48)

(49)

(50)
在式(49)和式(50)中所示的励磁控制规律,Idi和Iqi是很难测量的,但可以用可测量准确表示出来。由式(2)~式(4)可整理得到:

(51)

(52)
从式(51)和式(52)可看出,Idi和Iqi均可用易测量Pei,Qei和Ii表示出来,从而解决了控制规律的实现问题。

3.3 仿真案例与结果
为了验证SOSCCS的有效性,针对2种扰动,将其与2种经典的控制方案进行仿真对比:(1)励磁PSS+PID和调速PID分别控制方案;(2)线性最优综合方案(LOCC)。
3.3.1 外部扰动
在扰动发生前,系统处于稳定状态。在0.5~1.5 s时,系统受到外部干扰的作用。作用在发电机G2和G3的干扰分别为w12=0.05、w22=0.05、w32=0.05及w13=-0.05、w23=-0.05、w33=-0.05。系统在SOSCCS,PSS+PID和LOCC 3种不同控制器的作用下,有关状态量的响应曲线如图2和图3所示。

图2 外部扰动时发电机G2的系统响应曲线

图3 外部扰动时发电机G3的系统响应曲线
图2(a)、图3(a)、图2(b)和图3(b)表明,当发电机遭受外部干扰时,发电机机端电压和功角在SOSCCS作用下产生的静态偏移比在LOCC和PSS+PID的作用下的静态偏移均要小,这是由于SOSCCS对外部干扰有抑制作用。图2(c)、图3(c)、图2(d)和图3(d)表明, SOSCCS、LOCC和PSS+PID均使有功功率和机械功率变动到新的平衡点以适应外部干扰的作用。总而言之,SOSCCS使得发电机在遭受外部干扰时,不仅能比LOCC和PSS+PID更快地平息机组在暂态过程中的机械振荡,还能更好地抑制系统的超调,从而使得发电机具有良好的动态性能及鲁棒性。
3.3.2 三相短路扰动
在扰动发生前,系统处于稳定状态。在0.5 s时, 5号和8号母线之间的线路(靠近5号母线端处)发生三相金属性短路,故障持续0.15 s后被切除,在0.9 s时系统重合闸成功。当系统分别采用SOSCCS,PSS+PID和LOCC控制器时的系统有关状态量的响应曲线如图4和图5所示。
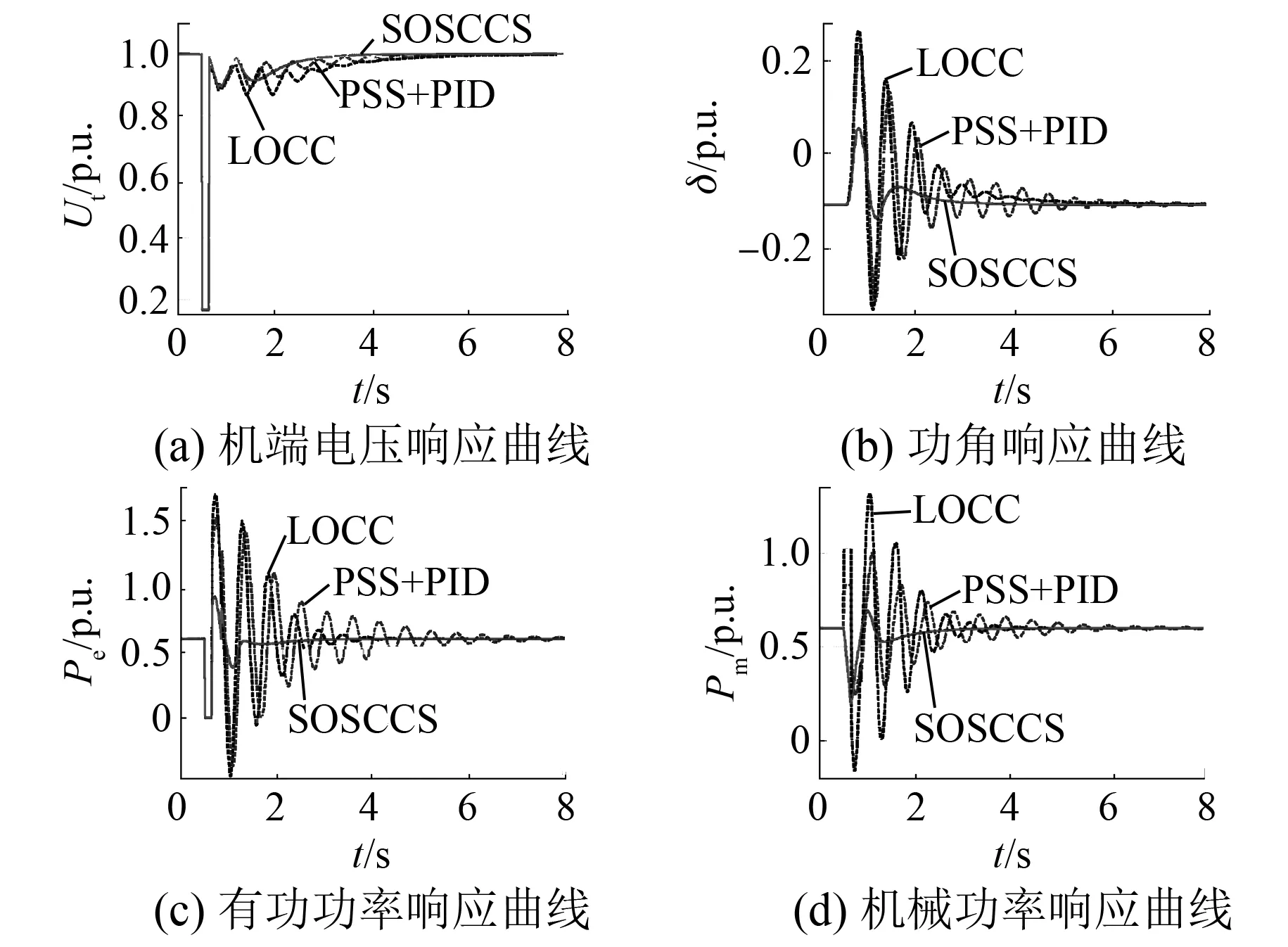
图4 三相短路扰动时发电机G2的系统响应曲线
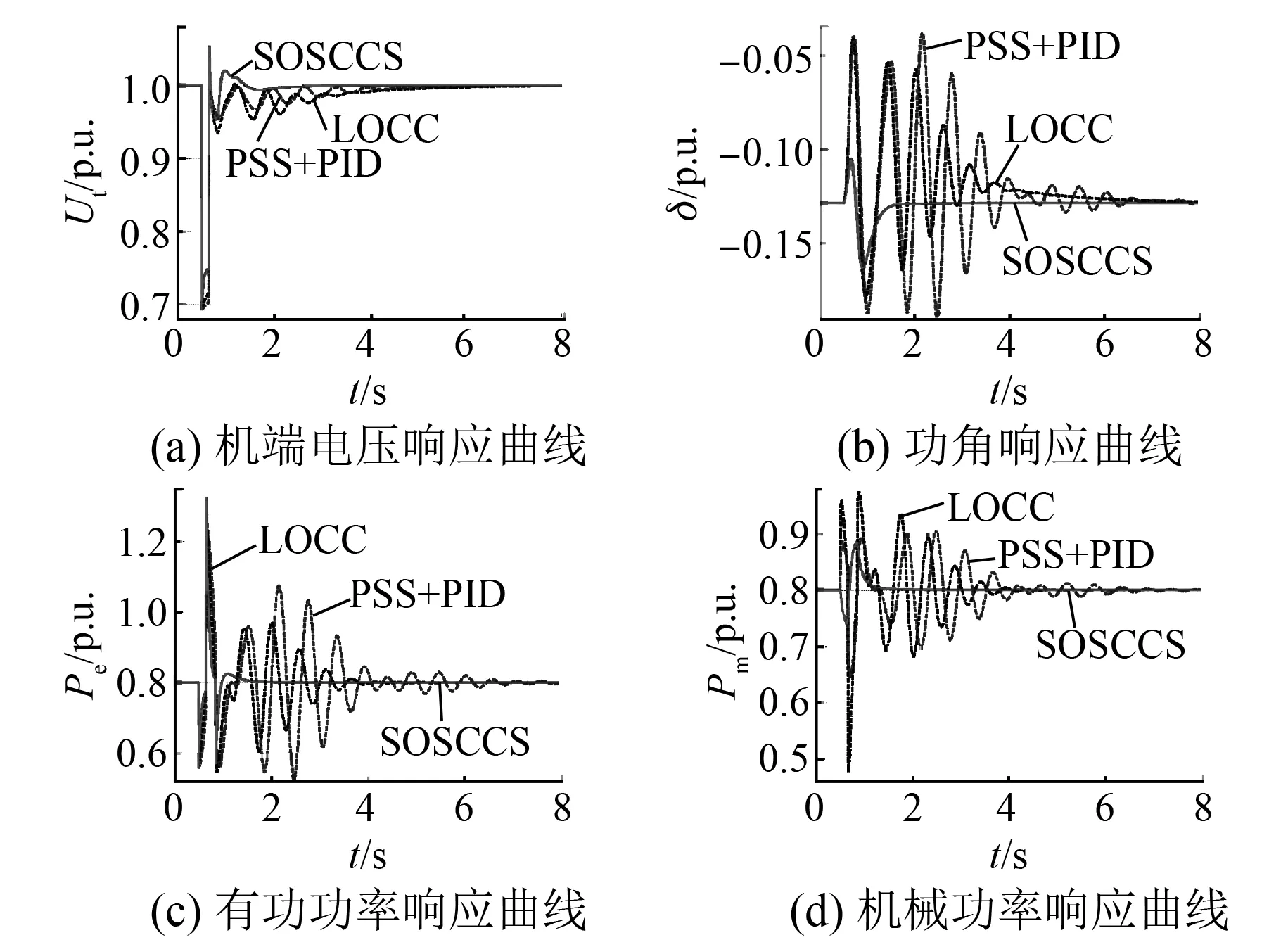
图5 三相短路扰动时发电机G3的系统响应曲线
图4(a)、图4(c)和图5(a)、图5(c)表明,当系统发生大扰动时,尽管发电机的机端电压和有功功率在3种控制规律的作用下都得到恢复,但SOSCCS比LOCC和PSS+PID能更快地恢复机端电压到初始水平,更早地平息有功功率的波动。图4(b)、图4(d)和图5(b)、图5(d)表明,SOSCCS比LOCC和PSS+PID能更好地平息系统频率振荡,更快地使系统返回初始运行点,更有效地抑制了系统的超调,使得发电机具有良好的动、静态性能。
SOSCCS,LOCC和PSS+PID这3种控制方案在发生三相短路扰动故障时的临界清除时间如下:
CCTSOSCCS=0.23 s,CCTLOCC=0.18 s,
CCTPSS+PID=0.17 s
(53)
式(53)表明,在3种控制方法中,SOSCCS最有效地提高了电力系统的暂态稳定性。
4 结 语
针对一个具有3台发电机的多机电力系统,建立包含调速回路和励磁回路干扰、不确定阻尼系数的鲁棒综合控制模型。运用SOSRCA,成功设计出多机环境下的发电机SOS非线性鲁棒综合控制策略。该方法根据李雅普诺夫直接法,选取经典的李雅普诺夫函数形式,建立一组状态相关不等式来保证多机电力系统的鲁棒稳定性及L2增益抑制性能。通过SOS分解技术的半定规划松弛算法可对该不等式组进行算法求解,从而得到系统的鲁棒综合控制规律。该控制器设计过程简单,无需包含参数估计器,从而降低了控制规律的复杂性。仿真结果表明,该控制律能够有效提高多机电力系统的暂态稳定性和鲁棒稳定性。

