几种防空导弹自动驾驶仪的研究分析

张 欧 严曙馨

江南机电设计研究所，贵阳550009

0 引言

在防空导弹领域，自动驾驶仪是飞行器的重要组成部分。导弹自动驾驶仪的设计根据其用途不同，可以分为过载驾驶仪和角度控制驾驶仪2类[1]。随着现代战争的需要，空袭武器正朝着隐身性能强、作战空域大、机动性能高等方向发展。防空导弹在大空域高机动飞行时，会产生大攻角，导致弹体气动参数剧烈的非线性变化和俯仰、偏航、滚动3个通道之间严重的交叉耦合，给导弹的稳定控制系统设计带来了困难[2-3]。

目前，使用较为普遍的是过载自动驾驶仪，用于防空导弹领域的结构主要有经典三回路过载控制结构[4-5]、伪攻角反馈三回路过载控制结构等[6-7]，这2种过载自动驾驶仪均采用角速率陀螺仪测量弹体角速度，线加速度计测量弹体过载，但由于结构不同，使得其控制效果和鲁棒性存在较大差异[1,8]。由大攻角、倾斜转弯技术和推力矢量控制等带来的复杂非线性气动特性也会改变导弹的静稳定性[2]。因此, 对自动驾驶仪的结构设计和静不稳定导弹的控制展开研究具有重要意义。

本文对经典三回路控制结构、伪攻角控制结构、改进的PI控制结构、改进的PD控制结构以及改进的PD控制结构+伪攻角控制结构这5种自动驾驶仪进行了研究分析。将理论推导和数学仿真结合，从系统性能分析、参数极点配置、控制性能指标等方面，系统地对比了5种过载自动驾驶仪结构的异同，研究结论为飞行器过载自动驾驶仪的选型和设计提供了参考。

1 弹体运动学

为不失一般性，本文讨论的导弹弹体为轴对称弹体，研究其纵向平面内的运动。若只考虑导弹弹体的刚性运动，忽略其弹性运动，通过对弹体采用“固化原则”和小扰动假设下的线性化[9]，则导弹纵向动力学可由短周期运动方程来近似描述，如式(1)所示[10]。

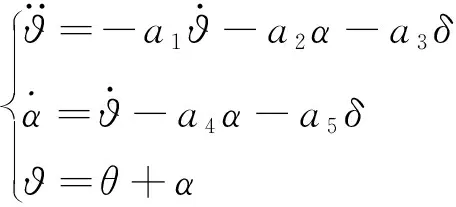
(1)

其中：a1为导弹的气动阻尼系数；a2为导弹的静稳定系数；a3为舵效率系数；a4为导弹的推力升力系数；a5为舵升力系数；α为攻角；θ为弹道倾角；ϑ为俯仰角；δ为舵偏角。

将式(1)写成状态方程形式为：

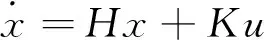
(2)

式中：

由式(2)表示的系统状态方程，可得系统的可控矩阵的行列式值：

(3)

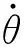
(4)

(5)

令A=a1+a4、B=a2+a1a4、C=a5、D=a1a5、E=a2a5-a3a4、F=-a3，则式(4)和式(5)可以变换为：

(6)

(7)

2 几种自动驾驶仪控制方法

2.1 经典三回路

在本文研究的自动驾驶仪中，假设舵系统和陀螺及加表的数学模型为全通环节，经典三回路的稳定控制回路原理图如图1所示。

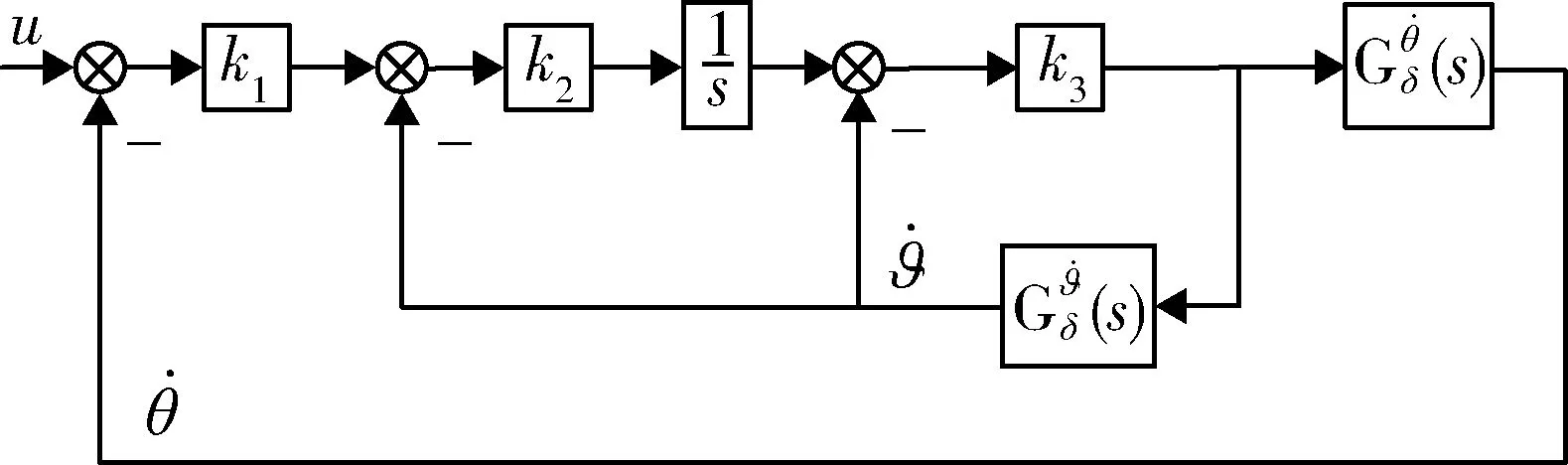
图1 经典三回路结构

经典三回路过载驾驶仪在国内外飞行器上均得到了普遍应用。从图1可知，经典三回路结构包含3个回路，即阻尼回路、增稳回路和过载回路；共有3个控制参数，即k1、k2和k3。经推导，可得到开环传递函数和闭环传递函数如下所示：

(8)

(9)

2.2 伪攻角结构

伪攻角结构的三回路过载驾驶仪也是一种三回路结构的过载驾驶仪，其结构框图如图2所示。对比图1和2结构可知，经典三回路结构中的增稳回路为姿态角反馈，而伪攻角反馈驾驶仪将角速率陀螺的测量信号经过一个惯性环节后得到近似攻角，并将其作为增稳反馈。

在伪攻角结构中，a′=E/F，因此只有3个控制参数，即k1、k2和k3。经推导，可得其开环传递函数和闭环传递函数如下所示：

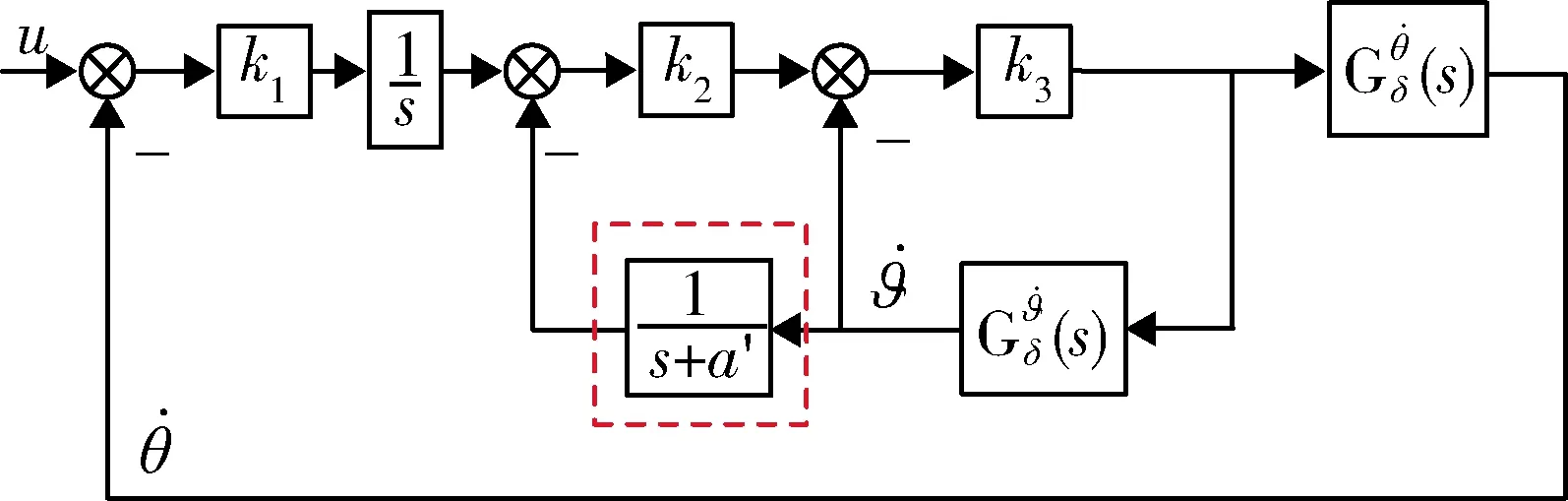
图2 伪攻角结构

(10)

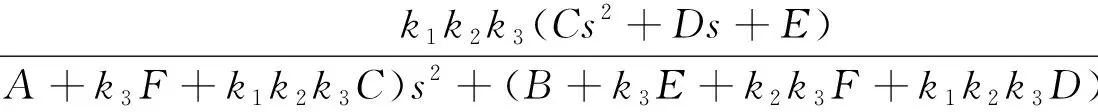
(11)

2.3 PI控制结构

改进的PI控制结构的自动驾驶仪框图如图3所示。与图1的经典三回路结构相比，PI控制结构把控制器k1换成了k1+kI/s。由图3可知，其有4个控制参数，即k1、k2、k3和kI，经推导，可以得到其开环传递函数和闭环传递函数分别如式(12)和(13)所示。

图3 PI控制结构

(12)

(13)

2.4 PD控制结构

改进的PD控制结构的自动驾驶仪框图如图4所示，与改进的PI控制结构类似，只是将积分环节kI/s换成了微分环节kDs。同理，其有4个控制参数，即k1、k2、k3和kD，其开环传递函数和闭环传递函数分别如式(14)和(15)所示。

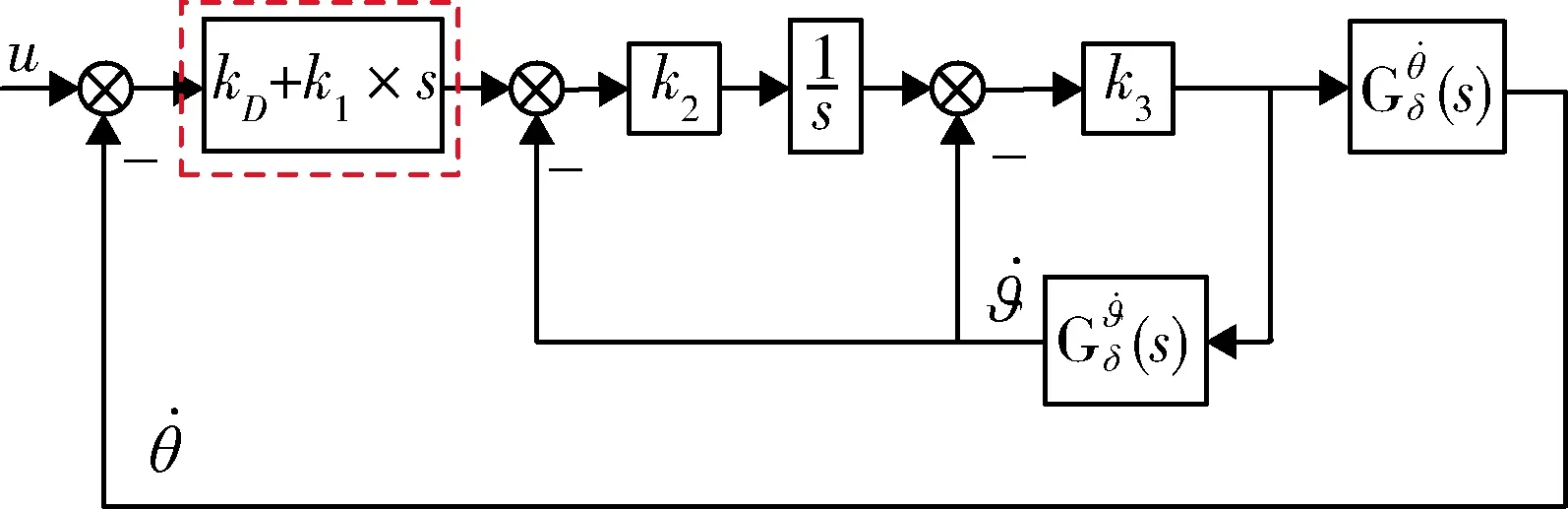
图4 PD控制结构

(14)

(15)

2.5 伪攻角+PD控制结构

顾名思义，伪攻角+PD控制结构就是结合了伪攻角结构的自动驾驶仪和PD控制结构的自动驾驶仪，其原理框图如图5所示。

图5 伪攻角+PD控制结构

在伪攻角+PD控制结构中，有k1、k2、k3和kD4个控制参数，其开环传递函数和闭环传递函数如下所示：

(16)

(17)

3 性能比较

3.1 系统性能比较

通过上一节的分析，可以得到5种不同自动驾驶仪的系统性能，如表1所示。由于系统的型别反映了系统对典型输入信号(如阶跃信号、斜坡信号、加速度信号等)无差的度量，由表可知，经典三回路结构和PD控制结构的系统型别最低，为0型，因此其跟踪典型输入信号的无差能力最差；而PI控制结构的型别最高，为Ⅱ型，所有其跟踪典型输入信号的无差能力最强。

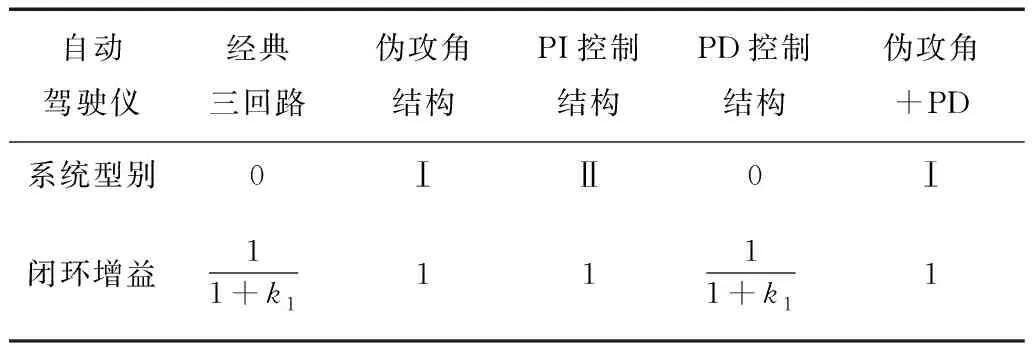
表1 不同控制结构的系统性能

从系统的闭环增益可以看出，经典三回路结构和PD控制结构的闭环增益为1/(1+k1)，需要增益补偿；而其它3种控制结构的闭环增益为1，不需要补偿。

3.2 实验结果比较

为了更好地对比5种自动驾驶仪结构的性能，采用参考文献[3]中的弹体气动参数作为本文的实验数据，如表2所示。可知，a2=-67.74，此被控对象是静不稳定的，加入阻尼回路，以稳定静不稳定弹体。

表2 弹体气动参数

利用表2中的弹体气动参数，对上述5种结构的自动驾驶仪进行了仿真实验，得到了图6～10的实验结果。其中，图6为单位阶跃响应曲线；图7为阻尼回路的Bode图；图8为单位舵偏响应曲线；图9为单位侧向角速度曲线；图10为单位舵偏角速度曲线。

图6 单位阶跃响应

图7 阻尼回路的Bode图

图8 单位舵偏响应曲线

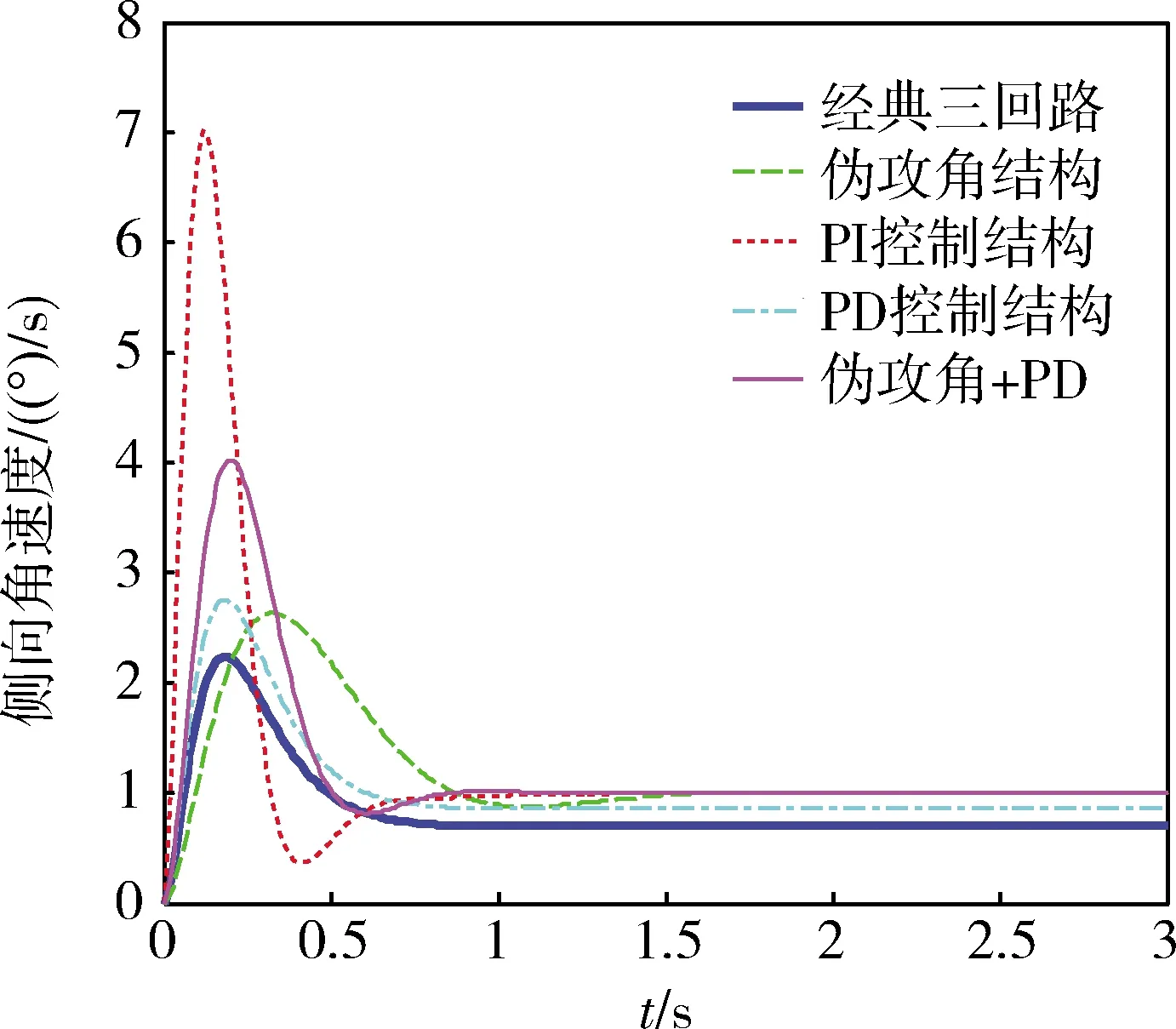
图9 单位侧向角速度

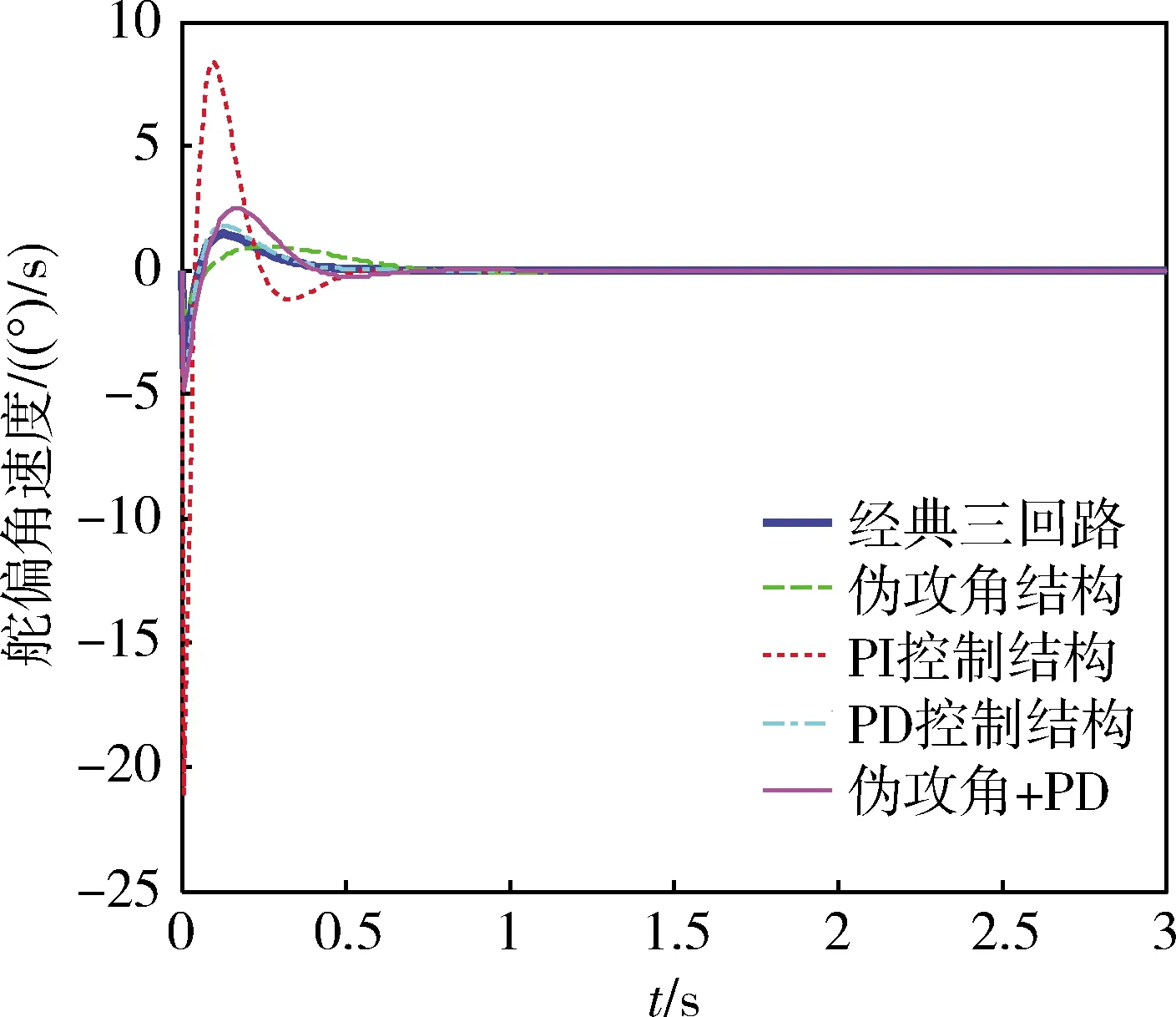
图10 单位舵偏角速度

在仿真中，通过极点配置得到了5种自动驾驶仪的控制器参数(表3)，由表可知，控制结构不同，则参数不同。表4为5种自动驾驶仪的稳定控制回路性能指标，可以看出PI控制结构的上升速度最快，但超调量最大，幅值裕度最低，截止频率最高；经典三回路的超调量最低，其值为0%；PD控制结构的相位裕度最高；伪攻角+PD控制结构的幅值裕度最大，截止频率最低，但相位裕度最低。

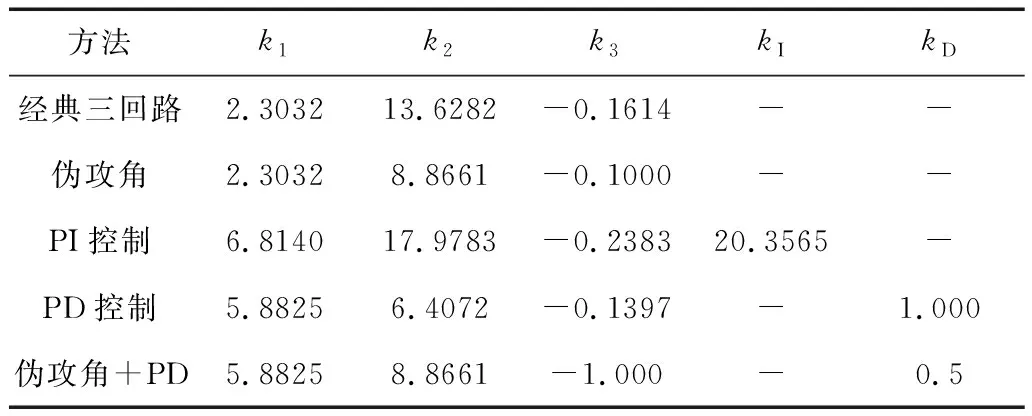
表3 控制器参数比较

表4 稳定控制回路性能比较

4 结论

介绍了5种控制结构的自动驾驶仪，即经典三回路控制结构、伪攻角控制结构、改进的PI控制结构、改进的PD控制结构以及改进的PD控制结构+伪攻角控制结构，并对其系统性能进行了理论推导分析。

通过对5种不同控制结构的自动驾驶仪的仿真分析可知，5种控制方法各有优缺点。相比于经典三回路结构，伪攻角控制结构在幅值裕度、相位裕度和截止频率方面性能更优，但上升时间最慢；PI控制结构除了上升时间最快之外，其余性能较差；PD控制结构和伪攻角+PD控制结构除了相位裕度和截止频率上差别大以外，其余性能相当，但考虑系统型别和闭环增益是否需要补偿，则伪攻角+PD控制结构的综合性能最优。