永磁同步电机改进型双矢量模型预测电流控制*
杨 锋, 胡明茂, 陈 鑫,2
(1.湖北汽车工业学院 机械工程学院,湖北 十堰 442002;2.奇瑞商用车有限公司,安徽 芜湖 241000)
0 引 言
永磁同步电机(PMSM)具有结构简单且控制精度高等许多优点,目前已经广泛应用于各种不同领域[1-2]。随着计算机和现代控制理论的发展,出现了许多不同的电机控制方法。矢量控制和直接转矩控制是应用最为广泛的控制方法,这2种方法也是到目前为止比较成熟的控制策略[3-5]。除了这2种方法之外,模型预测控制(MPC)越来越受到众多学者的关注。MPC可分为无限型和有限型控制集模型预测控制[6]。有限型控制集模型预测控制利用了电压型逆变器的离散开关状态进行优化。对控制对象进行仿真建模,计算出电机对开关状态的响应,并且对开关状态进行评估,选择出最佳响应对应的电压矢量作用到逆变器中。
然而传统的MPC在每个采样周期只能选择一个电压矢量作用到逆变器中,很难得到满意的系统稳定性。在此基础上,许多学者将占空比控制引入到传统的MPC策略中。文献[7-11]均是通过在传统的MPC中加入占空比控制,占空比是用零矢量和1个有效矢量进行的计算得到,该方法得到了良好的系统稳定性。但该方法也有缺陷,零矢量不一定得到全局最优,因此需要将电压矢量组合放到2个有效电压矢量,丰富了电压矢量的组合且增加组合的可能性。也有很多学者从多桥臂逆变器角度入手,来提高电机的稳态波动。文献[12]提出了一种五桥臂逆变器单矢量模型预测电流控制(MPCC),利用一个有效矢量和零矢量进行占空比计算,减少了电磁转矩的波动。文献[13]在文献[12]的基础上改进了占空比算法。主要利用无差拍原理,得到2台电机q轴电流跟踪到参考值需要的时间,选出合适的有效矢量,提高了系统的运行性能。文献[14]对电压组合所有的可能性进行评估,选择出最优电压矢量及其作用在电机上的时间,但是同时也增加了计算量。文献[15]通过q轴无差拍原理来解决电压矢量开关组合顺序问题,但开关组合的次数还是偏大,计算繁琐。
本文主要以PMSM为研究对象,在传统单矢量MPCC基础上,提出一种改进的双矢量模型预测电流控制(TV-MPCC),每个扇区用零电压矢量和1个有效电压矢量或者2个有效电压矢量合成1个期望电压矢量,从而增加电压范围覆盖方向和幅值,利用价值函数最小值原理,选出最优电压矢量。仿真表明所提出的方法具有较好的可行性和有效性。
1 PMSM数学模型
依据电机学原理,表贴式PMSM在旋转坐标系d-q下的定子电流状态方程可表示为[16]
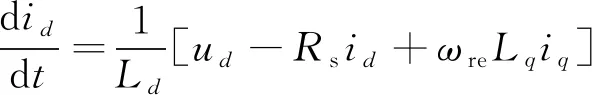
(1)

(2)
式中:ωre为转子电角速度;ψf为转子磁链;Ld、Lq分别为定子d、q轴电感;Rs为定子电阻;ud、uq分别为定子电压d、q轴分量。
通过欧拉法对式(1)和式(2)进行离散化处理可以得到:

(3)
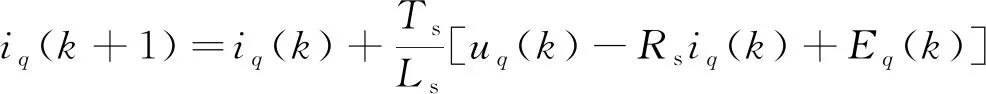
(4)
Ed(k)=ωre(k)Lsiq(k)
(5)
Eq(k)=-ωre(k)Lsiq(k)-ωreψf
(6)
式中:id(k)、iq(k)分别为在当前时刻d、q轴的电流值;id(k+1)、iq(k+1)分别为下一个采样时刻d、q轴的电流预测值;Ts为采样周期;Ed(k)、Eq(k)分别为在当前时刻d、q轴的电机反电动势;ud(k)、uq(k)为当前时刻d、q轴的电压值。
2 改进型TV-MPCC
在矢量控制中用到了2个电流环进行控制,而在传统的单矢量MPCC中只有1个速度PI环,这样PI参数的整定在很大程度上得以简化。MPC可以把不同的模型加入到价值函数中进行考虑,本文采用的控制目标为,电机d、q轴的电流能够跟随其参考给定值,以定子电流d、q轴分量与参考值的差的绝对值的和作为价值函数。

(7)
在1个采样周期中,有8种开关状态可以选择,其中包含了2个零矢量和6个有效矢量。在第i(i=0,1,2…7)个电压矢量作用下,结合电压重构,由价值函数预测下一时刻的d、q轴电流值。
2.1 TV-MPCC原理
本文提出的PMSM TV-MPCC在每个扇区的期望电压矢量通过2部分合成,第1部分期望电压矢量由一个有效矢量和零矢量合成,第2部分期望电压矢量由2个有效矢量合成。根据价值函数最小值原理,把这2部分得到的期望电压矢量代到价值函数中进行比较,最小值对应的期望电压即为最优期望电压。表1为有效电压矢量和零矢量合成期望电压矢量,表2为2个有效电压矢量合成期望电压矢量。

表1 有效电压和零矢量期望电压矢量合成

表2 两个有效值期望电压矢量合成
改进的MPCC框图如图1所示,控制策略采用的是id*=0,q轴电流给定值是通过速度环PI控制器得到。在模块TV-MPCC中,2部分的期望电压矢量作用时间ti,tj可以通过电流给定值和反馈值计算得到。
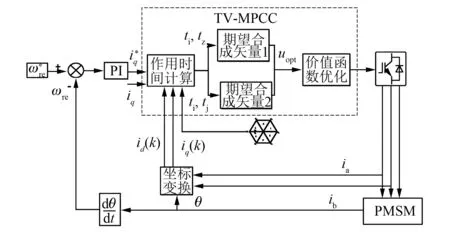
图1 TV-MPCC系统控制框图
2.2 矢量作用时间计算
在计算矢量作用时间时,不但需要考虑d轴无差拍跟踪,还需要考虑q轴无差拍跟踪。可以通过式(1)、式(2)得到零电压矢量作用的时间,dq轴电流斜率的计算式:

(8)
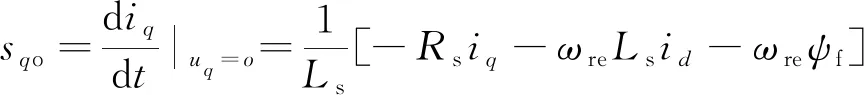
(9)
在式(1)和式(2)中,可以得到2个相邻的有效电压矢量ui、uj作用时,d轴和q轴电流的斜率为
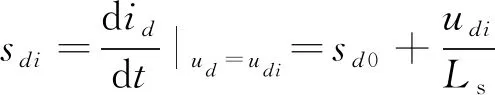
(10)
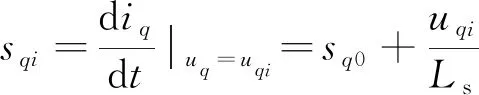
(11)
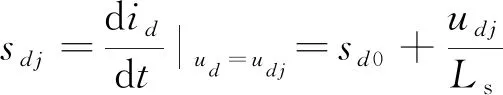
(12)
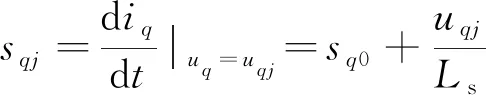
(13)
式中:udi、udj、uqi、udj分别为ui、ui在d、q轴的电压分量。
在第1部分中,采用有效矢量和零矢量进行作用。根据无差拍原理,下一采样时刻电流预测值等于给定值,因此d、q轴的电流预测公式可以改为
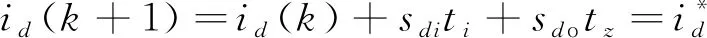
(14)

(15)
式中:ti为ui的作用时间;tz为零矢量的作用时间。
2个电压矢量作用总时间为Ts。即满足:
Ts=ti+tz
(16)
通过式(8)~式(16)可以得到:

(17)
tz=Ts-ti
(18)
计算出ti、tz以后,需要判断是否在0~Ts中,如果ti<0,则ui作用时间为0,全部由uj作用整个周期。若ti>Ts,则ui作用时间为Ts,uj作用时间为0。
在第2部分中,采用2个有效电压矢量进行作用。同理可得,d、q轴的电流预测公式可以改为
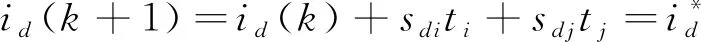
(19)

(20)
并且满足:
Ts=ti+tj
(21)
通过式(8)~式(13)和式(19)~式(21)可以得出:
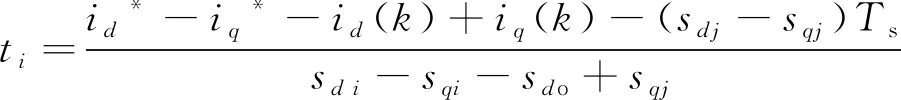
(22)
tj=Ts-ti
(23)
根据计算得到的ts、tj值进行判断。如果ti<0,则ui作用时间为零,全部由uj作用整个周期。若ti>Ts,则ui作用时间为Ts,uj作用时间为零。
2.3 期望电压矢量合成
由就近原则可知,期望电压矢量通过零矢量和有效矢量合成,或者通过2个有效矢量合成。每个扇区只能合成一个期望电压矢量,6个扇区可以合成6个期望电压矢量,因此通过12次预测选择出最优电压矢量。图2为零矢量和有效矢量合成图,图3为2个有效矢量合成图。

图2 零矢量和有效电压矢量合成图
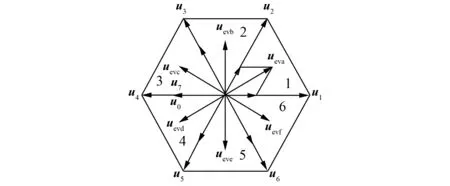
图3 2个有效矢量合成图
计算2部分期望电压矢量时,第1部分期望电压矢量可以根据式(17)、式(18)计算出零电压矢量和有效电压矢量作用时间,再根据式(24)和式(25)计算2个交轴的期望电压矢量分量:

(24)

(25)
同理,第2部分期望电压矢量可以根据式(22)、式(23)计算出2个有效电压矢量作用时间,再按照式(26)、式(27)计算2个交轴的期望电压矢量分量:

(26)
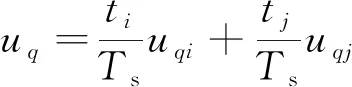
(27)
TV-MPCC策略具体步骤为
(1) 通过采样,得到当前时刻的电流值,再根据式(8)~式(13)得到电流率。
(2) 根据表1和表2选择基本电压矢量,用式(17)、式(18)、式(22)、式(23)计算得到2部分的作用时间。
(3) 根据式(24)~式(27)分别计算2部分电压矢量的d轴和q轴分量。
(4) 把2部分计算得到期望电压矢量的d轴和q轴分量代入到式(3)和式(4)中,分别得到2部分d轴和q轴的电流预测值。
(5) 把2部分计算出的电流预测值分别代入到价值函数中,将价值函数最小值对应的电压矢量作用到逆变器中。
3 仿真与分析
在MATLAB/Simulink环境中搭建仿真模型,验证改进的TV-MPCC算法的有效性和可行性,并对仿真结果进行研究分析,表3给出了仿真时PMSM的主要参数。

表3 PMSM主要参数
为了证明本文算法的可行性,在同样条件下搭建传统单矢量MPCC系统仿真模型,采样时间为0.000 01 s。仿真时间为1 s,在0.6 s时施加负载10 N·m,在0.8 s时负载突变为5 N·m。输出的转矩如图4所示。
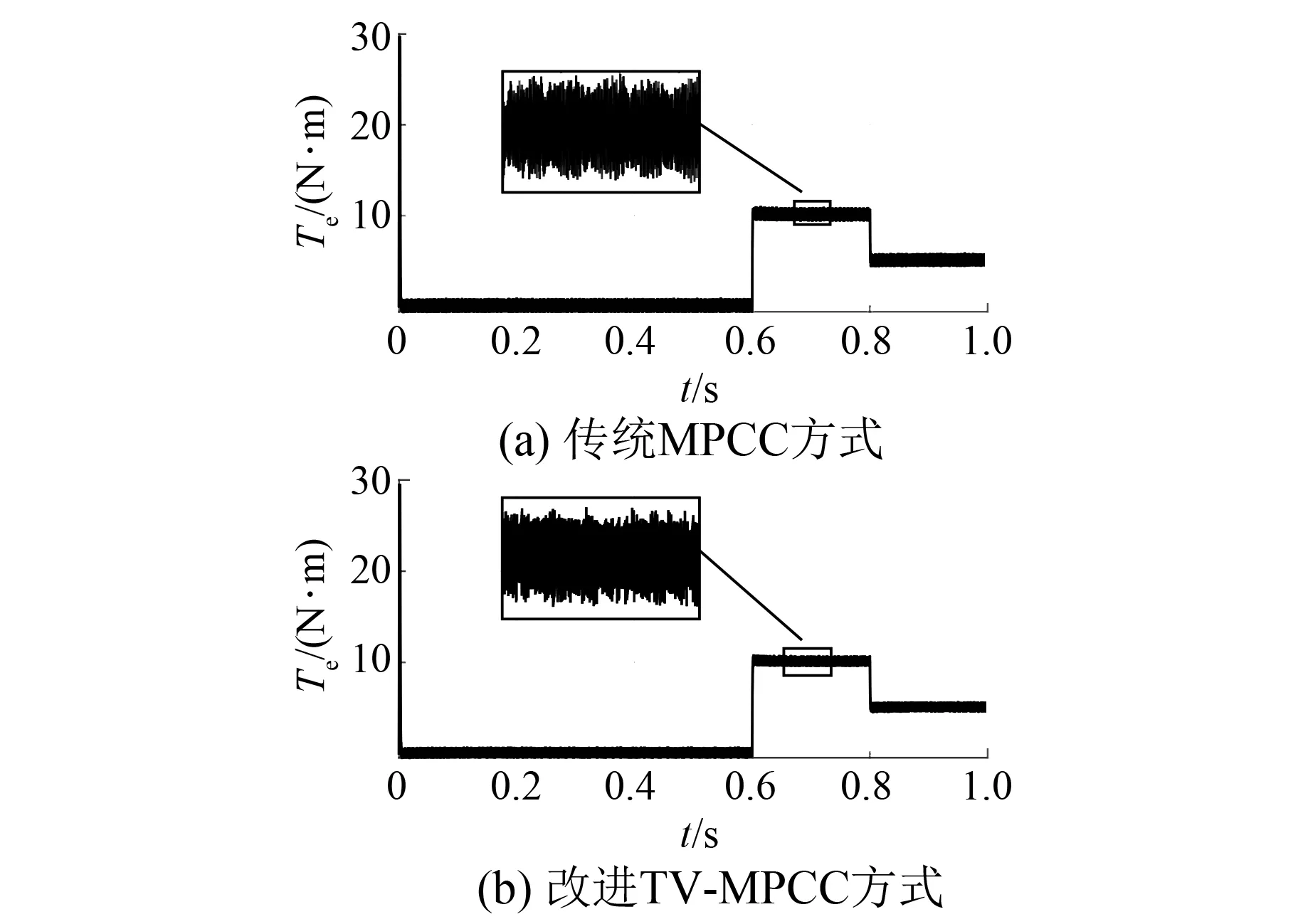
图4 MPCC转矩波形
图4(a)中传统的单矢量MPCC仿真结果图显示,当转矩发生突变时,转矩波动较大。采用TV-MPCC时,由于双矢量控制增加了2个有效矢量合成和有效矢量与零矢量合成,再从其中选出最优矢量,最优矢量可选范围增加。与传统MPCC相比,空载时稳态下的转矩误差(标准差)减小了4.4%,负载为10 N·m时,转矩误差减少了3%,转矩误差负载为5 N·m时,减少了4.68%。说明了本文提出的方法对转矩稳态性能有一定的提高。
图5给出了传统MPCC和改进TV-MPCC的转速波形,电机起动时,改进的TV-MPCC的转速超调量和传统控制方法相差不大。当波形稳定时,两者波形基本没有波动。证明了改进TV-MPCC对电机起动后转速环性能没有影响。
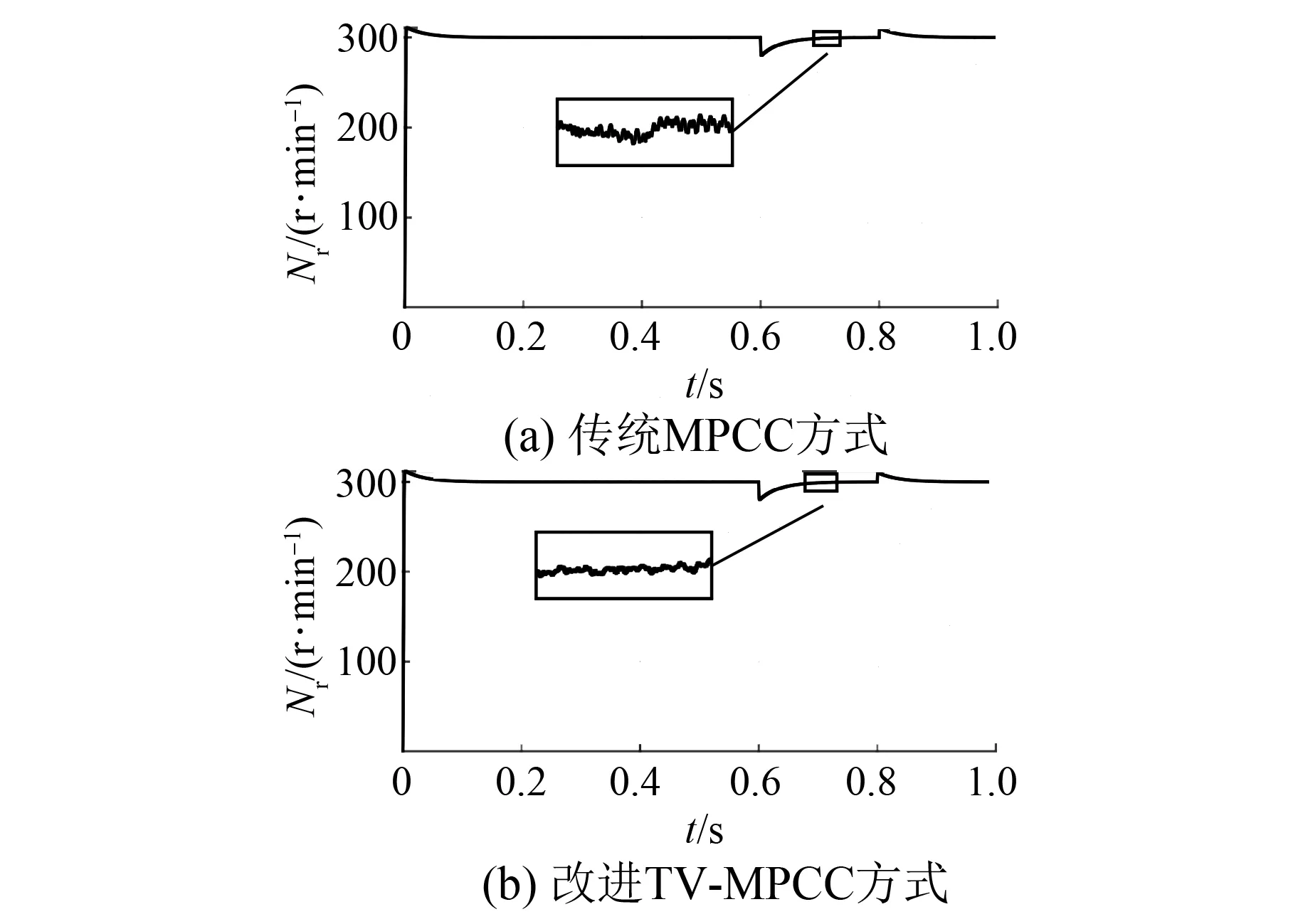
图5 转速波形
图6为2种方法的d、q轴电流波形。改进TV-MPCC在起动后,很快达到了稳态,在稳态时改进TV-MPCC的电流和转矩比传统MPCC幅度有所降低。由图7可以看出a相电流波动也有所降低。

图6 d、q轴电流波形

图7 电机定子a相电流波形
为了将不同控制方法的误差值进行对比,用To Workspace模块将Simulink中传统的转矩id,iq轴的电流数据和改进后的转矩,id、iq轴的电流数据传到MATLAB工作区,形成离散数据。再用std函数(标准差函数)分别求出它们在0~0.6 s,0.6~0.8 s,0.8~1.0 s的标准差。标准差计算公式为
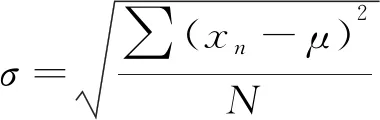
(28)
式中:σ为标准差;xn为某一时刻的转矩或者电流值;μ为本组数据的平均值;N为本组数据的总个数。
表4显示了不同控制方法的误差。
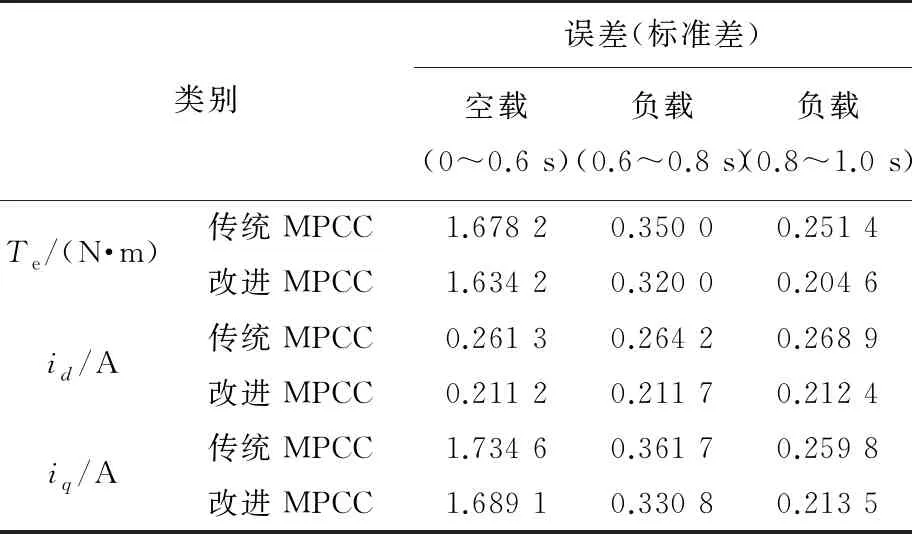
表4 不同控制方法的误差
结合图6和表4可以看出,改进TV-MPCC对id、iq轴电流有明显的控制效果。由此可以证明改进TV-MPCC的有效性。
4 结 语
本文在传统单矢量MPCC基础上,提出了一种改进TV-MPCC策略。在改进型控制策略中,期望电压通过零矢量和有效矢量合成,或者通过2个有效矢量合成。根据价值函数最小值原理,在期望电压矢量中选出最优电压矢量。提出的TV-MPCC对比传统单矢量MPCC,能够降低电流脉动,实现无差拍控制。系统的稳定性在一定程度上得到改善,提高了电流的控制精度。

