基于关联规则与PLC的同步电机高精度转角自适应控制方法

刘震宇

(国网冀北电力有限公司 承德供电公司,河北 承德 067000)

0 引 言

在机械领域，同步电机应用十分广泛，在更高效地应用电机的研究与设计中，如何控制其转角的精度成为了一个十分热门的研究领域。然而由于转角对精度的高要求，很多粗略的算法在智能控制转角的过程中，很难保证实际稳定性，因此需要寻找更好的同步电机高精度转角自适应控制方法。

文献[1]通过设计基于TIA和PLC的变频恒压供水自动控制系统，并应用于实际生产中，实现仿真软件360°的低误差旋转，然而由于该模型在电子信号与机械模型之间的连通性能较差，难以保证计算机仿真的结果与实际数据相匹配。文献[2]提出了基于Super-twisting算法的永磁同步电机自适应滑模速度控制，通过积分因子的跟踪，计算精度误差，并以自适应的优化算法提高精度的准确性，但是这种控制方法难以保证电机运行的稳定性，十分容易被反向操作的误差控制。文献[3]提出基于气隙磁场调制理论的永磁同步电机磁场分析与特性对比，利用电机的凸起端建立了一个模型参考的滤波器，通过计算电机参数的强度，逐步稳定地实现滑模观测。这种方法的缺点在于计算强度十分大，需要配置较高的计算设备，并且运算速度和算法的响应速度非常慢。本文综合以上文献，通过对数据库中文献资料的对比，基于关联规则算法与PLC程序，建立了同步电机高精度转角自适应控制方法，计算同步电机转角理想传动比，基于关联规则优化转角控制增益系数，PLC则通过将控制指令输入到控制器的存储器中，然后进行存储和执行，完成同步电机高精度转角自适应控制，通过试验验证了该控制方法在实际中的应用效果优于常规方法。

1 基于关联规则与PLC设计同步电机高精度转角自适应控制方法

1.1 计算同步电机转角理想传动比

在计算同步电机的理想传动比时，可以将关联规则算法和PLC代入其中，目前可将PLC技术应用于各个领域，通过与计算机、现代机电等先进技术的结合，为各领域的工作交流奠定基础，突出了在工业生产过程中的重要应用优势。在电气自动化设置中选择合理的PLC技术，可以对此类同步电机工程的设计和应用等具体情况进行实时控制。在运行过程中，PLC技术的合理应用是对电机、电路、电源等进行合理调整的关键因素，并能在该技术的应用模式下，实现对电机使用具体情况的实时监控，从而根据对电流的要求实时调整变频器，为节能标准的实施与整体工作效率的提高提供基础条件。设增益角速度为Hk，则可以得到同步电机的增益效率为

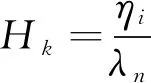
(1)

式中:Hk为同步电机的传动过程中，理想状态下的增益角速度；ηi为同步电机的高精度转角角度；λn为同步电机在匀速状态下的横向摆动幅度[4-5]。

将比值加权处理，可以得到：

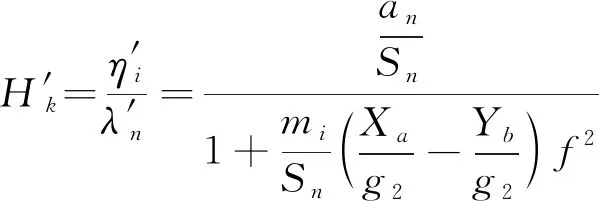
(2)

式中:an为同步电机在匀速状态下的侧向加速度；Sn为同步电机在匀速状态下行走一圈达到的距离；mi为同步电机的转子质量；Xa为同步电机在X轴方向的速度分量；Yb为同步电机在Y轴方向的速度分量；g2为同步电机稳态系数；f2为同步电机的稳态加速度增益系数[6-7]。

通过式(1)、式(2)可以看出，理想传动比可以通过同步电机的转角转速而变化，如果转角过于灵敏，则很难判定转角转速的具体数值，因此可以设置一个理性状态，将转角的转速设为0，则：

(3)

式中:Imin表示当同步电机的转角转速为0时，理想传动比的数值；ηimax表示同步电机运行到最大值时，临界状态下的转角转速；λimax表示同步电机运行到最大值时，临界状态下的转角移动距离[8-9]。由此可以得到同步电机的理想传动比。

1.2 基于关联规则优化转角控制增益系数

由上文可知理想传动比的加权组合，可以被称为单项指标的性能评价对象，由此可以建立管理数据库，且计算关联规则中的综合评价指标为

(4)

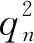
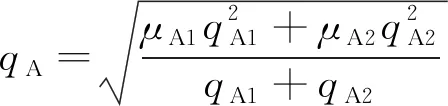
(5)

式中:μA1和μA2表示考虑实际情况后的同步电机转角运行惩罚因子；qA1和qA2表示在关联数据库中，A项指标的跟踪误差。在关联规则数据库中综合评价值qB同理可得：

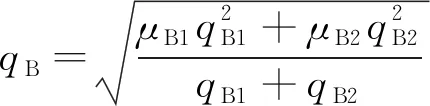
(6)

式中:μB1和μB2为考虑实际情况后的同步电机转角运行惩罚因子；qB1和qB2为在关联数据库中B项指标的跟踪误差[11];qC与qD同上。

综上所述，转角控制增益系数就可以通过关联规则中的综合评价指标求得。

1.3 设计转角模糊自适应算法

通过上文中的增益系数，可以直接得到自适应算法的模糊最优值，以此判定对转角控制效果的改善程度，控制器的搭建自适应模型结构如图1所示。

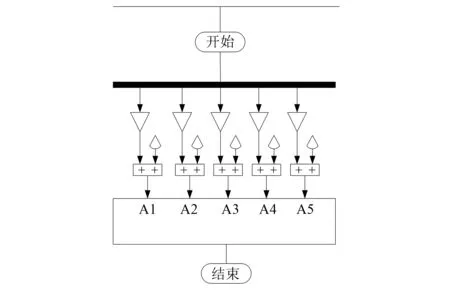
图1 自适应模型结构

在图1中，A1～A5分别表示A项指标中的5个指标系数。通过图1的模型结构，可以得到同步电机中的转角质心偏离距离：

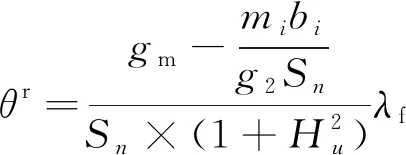
(7)

式中:θr为在上文的自适应模型结构中，同步电机的转角偏离距离；gm为同步电机转角旋转的离心加速度；mi为同步电机的转子质量[12]；bi为转角旋转的速度；Sn为同步电机转角旋转一周所行走的距离；Hu为质心偏移角与中心点的角度误差；λf为同步电机的综合稳定系数[13-14]。

综上，可以建立同步电机转角的模糊自适应算法结构流程，此时，还需要将该算法的适应性系数增加到数据集中，以便判断同步电机的高精度转角自适应算法是否能够停止迭代。算法结构流程如图2所示。

图2 算法结构流程图

需要建立关联规则数据集，将同步电机转角理想传动比代入到数据集中，然后将数据编串成码，得到同步电机转角的基础参数。通过单一数据的计算与数据集的整体计算，可以得到整体的数据统计结果，由式(8)判断是否满足了迭代的终止条件：

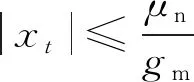
(8)

式中:xt为同步电机高精度转角的算法适应性参数；μn为转角周边与同步电机相邻部位的附着系数；gm为当地的重力加速度[15]。若满足以上不等式，则可以直接退出，并输出结果，若不满足条件，则需要重新建立数据集。

2 测试与分析

2.1 算法模型

对同步电机的高精度转角自适应控制进行测试,将上文中设计的自适应控制方法与常规的3种方法进行对比，通过检验算法与同步电机的适应性，得到控制算法的检验结果。试验用同步电机内部结构如图3所示。

图3 同步电机结构

建立算法模型，其中计算机设备的操作系统为Windows 10，并使用intel i5-2240@3.42 GHz以上的中央处理器(CPU)作为设备的主频，内存4 GB以上，储存空间大于600 GB，通过结构化查询语言(SQL)建立一个数据库作为试验过程中使用的数据来源，最后使用MATLAB作为计算工具计算试验得到的数据结果。在计算算法与实际结构的适应度时，需要通过以下算式：

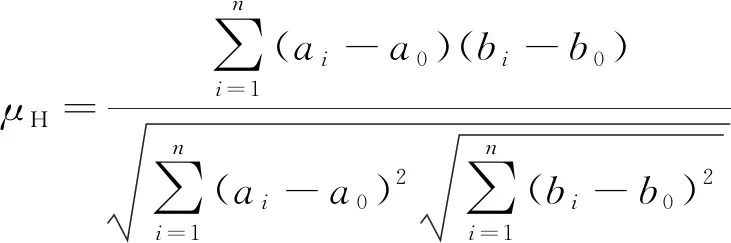
(9)

式中:μH为以上进行测试的4种算法对于实例分析的适应度，其值域区间为[0，1]；ai为在电流信号的刻度为i时，算法的适应度；a0为算法适应度的极值；bi为当电流信号的刻度为i时，该算法的适应度；b0为算法适应度的极值[16]。通过式(9)计算4种算法的适应度系数，并以转角的度数为变量，进行试验分析。

2.2 算法适应性测试

使用上文中设计的试验方法，设定转角的度数为10°、30°、45°、60°，将文中设计的算法作为试验组，将文献[1-3]方法作为对照组，进行算法效果的测试。最后通过MATLAB软件进行计算，将计算结果绘制成图像如图4所示。

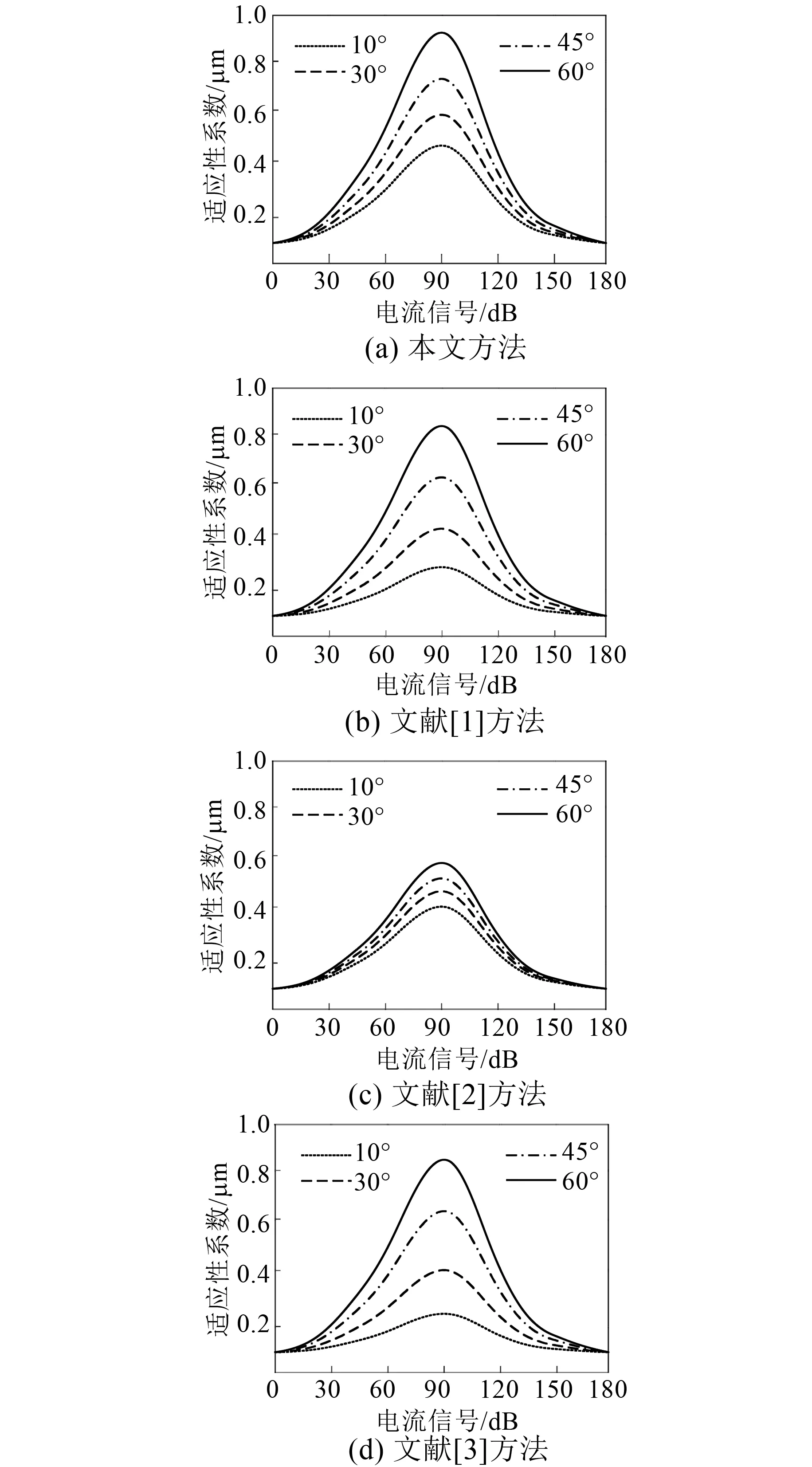
图4 算法效果测试

由图4可知，四幅图像的极值点均在电流信号为90 dB时，且均有转角度数作为变量的4个曲线。在试验组本文方法的图像中，当转角度数为10°时，适应性系数的极值为0.93 μm，当转角度数为30°时，适应性系数的极值为0.72 μm，当转角度数为45°时，适应性系数的极值为0.58 μm，当转角度数为60°时，适应性系数的极值为0.49 μm。在文献[1]方法中，适应性系数分别为0.82、0.63、0.41、0.29 μm，文献[2]方法的适应性系数分别为0.58、0.53、0.48、0.40 μm，文献[3]方法的适应性系数分别为0.86、0.63、0.40、0.25 μm。由此可见，随着转角度数的增加，适应性系数会相应减小。为了保证试验结果的准确性与稳定性，不受到随机数据的干扰，反复进行10次以上试验，计算平均值，如表1所示。

表1 适应性系数的平均值对比结果 μm

表1所示为10组试验中适应性系数的极大值与极小值。通过计算，可以得到本文方法适应性系数的平均值为0.48/0.92 μm，文献[1]方法的平均值为0.27/0.82 μm，文献[2]方法的平均值为0.42/0.57 μm，文献[3]方法的平均值为0.26/0.86 μm。综上所述，试验组中适应性系数的极大值与极小值均高于3个对照组，文中设计的转角自适应控制方法优于常规方法，能够在实际中拥有更高的精度。

3 结 语

本文在计算理想传动比的基础上，将实际同步电机中基于关联规则的数据代入到模型中，并建立了一个自适应的补偿策略，以控制实际精度变量。综合所有公式，建立了相应的算法，并通过对比试验验证了该算法的实际效果，所设计基于关联规则与PLC的同步电机高精度转角自适应控制方法随着转角度数的增加，适应性系数会逐渐减小，其适应性系数极大值与极小值均高于文献方法。