工程实践背景下的周期性方波信号分解与合成

杨亚莉

（武汉纺织大学 电子与电气工程学院，湖北 武汉430200）

0 引言

工科大学生，作为承担国家建设任务的工程师的储备力量，在大学期间，要逐步通过专业课程的学习和实践，从中学阶段的理论思维转入联系实际的物理思维，进而形成构建性的工程思维［1］。

“信号与系统”课程是电子信息类专业的一门非常重要的核心基础课程，主要内容可概括为信号分解和系统分析。

信号分解是系统分析的基础。其中，信号的频域分解，也即频谱分析的目的是把复杂的时间历程波形，经过傅里叶变换分解为若干单一的谐波分量来研究，以获得信号的频率结构以及各谐波和相位信息，进而可以对信号的信息作定量解释。

傅里叶级数分解是频域分解的基础，也是带领学生从理论思维转入物理思维，进而形成构建性的工程思维的一个实例。

1 周期信号的傅里叶级数分解

在讲授傅里叶级数时，先要让学生能转换看问题的角度，所谓“横看成岭侧成峰，远近高低各不同”，再就是要让学生明白“频谱”的概念（以时域波形，也可叫“时谱”作对比），频谱图上反应了信号的什么信息。将周期信号进行傅里叶分解后，傅里叶级数中各个子信号其实就是各个频率分量，而各个子信号的系数的模就是各个频率分量的幅度。频谱图反映的是信号包含了哪些频率分量以及各个频率分量的幅度（含量）。经过这样讲解，学生就很好地理解了频谱图的工程意义［2］。

根据傅里叶分析理论，若函数 满足狄里赫利（Dirichlet）条件：

（1）在一周期内，如果有间断点存在，则间断点的数目应该是有限个；

（2）在一周期内，极大值和极小值的数目应是有限个；

则该函数可以展开成如下形式的傅里叶级数：

其中，ω1=2π/T，cn为各项系数，φn为各项相位。图1所示幅值为A，周期为T的方波信号，其傅里叶级数为：

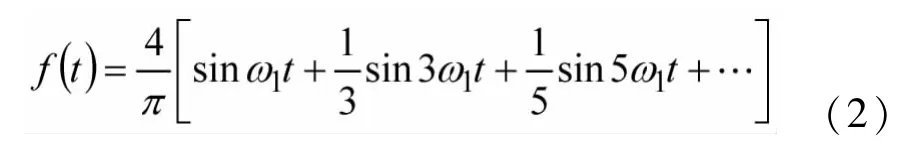
图1中的虚线正弦曲线为从原始方波信号中提取的1，3，5次谐波分量，即（2）式的前3项；实线振荡信号为由该3项正弦波合成的信号。当取的谐波的项数越多时，其合成的信号越接近方波信号。但由于吉布斯现象的存在，合成信号在方波信号跳变沿始终会有一个峰起值，该峰起值趋于一个常数，它大约等于总跳变值的9%，并从不连续点开始以起伏振荡的形式逐渐衰减下去［3］。

图1 周期性方波信号分解和合成示意图

2 周期信号波形分解与合成的硬件实现

在充分理解并掌握了周期性信号的傅里叶级数分解的意义和方法后，借助实验室的硬件设备，结合“模拟电子技术”和“单片机原理与应用”等相关专业课知识，带领学生进行周期信号波形分解与合成的硬件实现，充分锻炼学生的工程能力［4］。

2.1 系统总体方案设计

利用文氏电桥振荡电路产生频率为10 kHz的正弦波，再经过过零比较器便可输出方波。此方案电路较为复杂，但频率和占空比都能较好地控制，输出波形稳定，频率精度高。

选用高阶有源集成滤波器。LTC1562是凌特公司的单片有源集成RC滤波器。利用LTC1562构成八阶巴特沃斯带通滤波器，外围电路只用匹配电阻、电容，电路简单，并且选频特性良好。

采用有源全通滤波器。全通滤波器对信号的幅度没有影响，但可以改变输出信号的相位。通过调节电路中的电阻阻值可以改变输出信号与输入信号的相位差。该方案能够很好地实现信号的移相。

信号叠加电路，选用TI公司的高精密、低噪声运放OPA227做加法电路。将产生的具有一定幅度和相位关系的三路正弦信号进行叠加，产生近似方波。由此确定整个系统的设计方案，系统总体框图如图2所示。

图2 系统硬件实现总体框图

2.2 各模块设计与实现

1）方波振荡电路

方波振荡器如图3所示，方波振荡电路由文氏电桥振荡器和滞回比较器构成，文氏电桥振荡电路选用TI的低噪声高精密运放OPA277，产生频率为10 kHz的正弦波，再经过比较器便可以输出10 kHz的方波。由于将输出的正弦波直接经过LM311比较器后输出的方波占空比不为50%，因而将输出的正弦信号叠加一直流偏置来改变比较器输出方波的占空比，直流偏置电压通过电阻分压得到，调节滑动变阻器R9可以将占空比调整到50%。

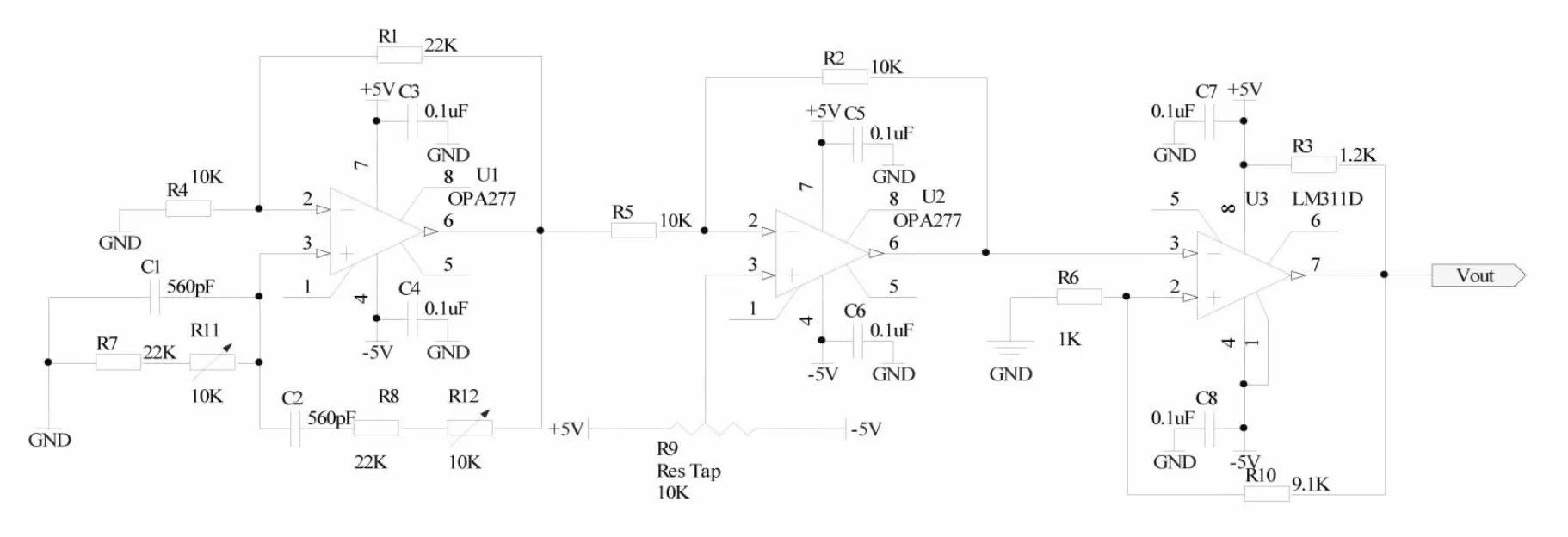
图3 方波振荡器电路图

2）分频与滤波电路

分频与滤波电路采用LTC1562接成八阶巴特沃斯带通滤波器实现。LTC1562的中心频率从10 kHz至150 kHz可调，精度为0.5%，其带宽、Q值及增益均可用电阻进行调节。根据题目要求，采用LTC1562分别实现中心频率为10 kHz、30 kHz、50kHz的带通滤波器，进行选频滤波，最后输出10 kHz、30 kHz、50 kHz正弦信号。中心频率10 kHz带通滤波器电路图如图4所示。

图4 10 kHz带通滤波器电路图

3）移相电路

恒幅移相电路选用TI的低噪声、低电压精密运放OPA211，通过调节电位器R3便可以改变输出信号的相位，相位可调范围为0°到180°，两个移相电路串联可以实现0°到360°的相位调节。经测试三路信号的相位差均在180°之内，故每路信号只需一个移相电路。移相电路图如图5所示。

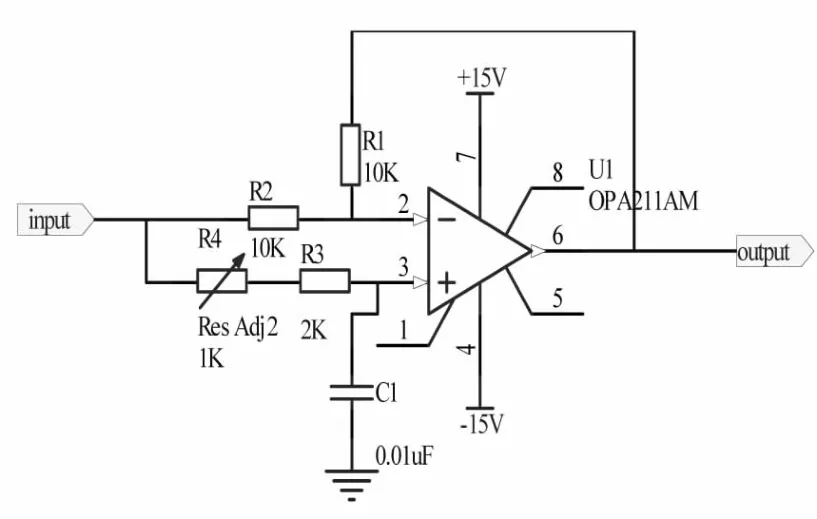
图5 恒幅移相电路图

4）信号叠加电路

选用TI公司的高精密、低噪声运放OPA227做加法电路。将产生的具有一定幅度和相位关系的三路正弦信号进行叠加，产生近似方波或三角波。信号叠加电路见图6。

图6 信号叠加电路

2.3 测试结果

在60M数字示波器DS5062上显示的方波波形合成实验的显示结果图，如图7和图8所示。

采用4位半数字万用表VICTOR8155和60M数字示波器DS5062M进行测试，用示波器测量所产生的正弦信号的频率，用4位半数字万用表测量正弦信号的幅度。测试结果见表1。

经过示波器实测10 kHz、30 kHz、50 kHz的正弦信号频率稳定，无失真。10 kHz正弦信号与30 kHz的正弦信号合成的波形与理论上的波形一致，10 kHz、30 kHz和50 kHz正弦信号合成的波形与实际方波更加接近。

3 结语

大学教育，带给学生最宝贵的财富，应该不只是课堂上学到的知识，更多的是一种思维方法。其中工程思维和实践能力的培养，对工科大学生学习能力和创新能力的提升具有十分重要的作用。“工程思维是介于理论思维与实践之间的桥梁”，其显著特征是构建，即应用知识创造世界。工程思维是人类最常见、最重要的思维方式之一；在工程教育中，工程思维方式的教育和培养是最核心的任务和内容之一［5］。

本文以周期信号的傅里叶级数的讲解为例，从理论和软硬件实践上全方位地阐述信号的分解与合成，引导学生从中学阶段的理论思维转入联系实际的物理思维，进而形成构建性的工程思维，培养了学生的工程实践能力。