一种面积优化的ZUC算法的硬件架构

陆 斌，严利民

(上海大学 微电子研究与开发中心，上海 200444)

作为序列密码体系之一的祖冲之(Zu Chongzhi, ZUC)密码是由我国自主设计的首个成为国际标准的密码算法，主要用于无线通信领域的信息安全[1].随着物联网技术的发展，在资源有限的物联网终端中保障信息安全的工作对密码算法提出了更严苛的要求[2-3]，因此设计更少资源开销的ZUC密码架构具有现实意义.

ZUC密码的核心和主体是ZUC算法，以及以ZUC算法为基础的完整性算法128-EIA3和机密性算法128-EEA3[4].目前除了一些ZUC算法的直接硬件实现[5]，也有许多文献对ZUC算法硬件架构进行了进一步研究： Wang等[6]对ZUC算法的线性反馈移位寄存器(Linear Feedback Shift Register, LFSR)设计了四级流水线以降低关键路径延时，实现了较高的运行频率，但是其硬件开销较大；Zhang等[7]提出了基于进位保留加法器(Carry Saved Adder, CSA)结构的LFSR以及并行运算的模(2311)加法单元，可以在不使用流水线的情况下有效降低关键路径的延时；Liu等[8]在此基础上设计了二级混合流水线机构，能够进一步提高ZUC算法的运行频率.

上述研究主要致力于优化LFSR从而降低关键路径延时提高性能，但是很少涉及S盒部分的优化.S盒在ZUC算法中占据了较多的资源开销，32 bit的S盒由4个8 bitS盒并行组合而成，其中S0和S2为同一个S盒(S0-box)，S1和S3为同一个S盒(S1-box).在上述的研究文献中S盒基本上由查找表的方式实现[5-8]，导致了较多的硬件开销或是额外的存储资源.ZUC算法的S0-box本质上是一个3层Feistel结构[9]，而S1-box与AES(Advanced Encryption Standard)算法的S盒构造上几乎相似，可以参考AES算法的S盒研究方法[10]对其进行优化.

因此，本文综合考虑了面积与延时两方面因素，提出了一种面积优化的ZUC算法的硬件架构，该架构在文献[7]的基础上提供了两方面的改进： 一是设计了基于复合域运算的S1-box结构；二是提出了一种基于超前进位加法器(Carry Lookahead Adder, CLA)的模(2311)加法单元，从而有效降低了ZUC算法硬件实现的资源开销.

1 基于复合域运算的S1-box的设计

1.1 S1-box的整体设计

ZUC算法的S1-box是基于数学上的有限域运算和仿射变换组合实现的[9]，如式(1)所示：

F=Mx-1⊕B.

(1)

式中：x为8 bit输入向量；x-1为GF(28)域(由不可约多项式M(x)=x8+x7+x3+x+1定义)上的乘法逆运算；⊕为异或运算；M和B分别为仿射变换过程中的仿射矩阵和常向量，且

(2)

式(1)中在GF(28)域上求乘法逆运算的实现是最为复杂的部分，由于S1-box与AES算法的S盒构造上的相似性，因此参考AES算法的S盒研究方法[10]将有限域上的求逆运算同构映射转换复合域上，可以有效简化电路复杂度.考虑到同构映射的复杂度与优化效率[11]，本文将转换到复合域GF((24)2)上进行求逆运算.

由此式(1)可以写成式(3)的形式：

F=M(δ-1(δx)-1)⊕B.

(3)

式中：δ为有限域GF(28)至复合域GF((24)2)的同构映射矩阵；δ-1为δ的逆矩阵.基于式(3)，ZUC算法的S1-box的结构框图如图1所示.

图1 S1-box的硬件框图Fig.1 Hardware block diagram of S1-box

1.2 复合域的乘法逆运算过程

根据有限域基础知识[12]，基于不可约多项式p(y)=y2+y+υ和标准基{γ1,γ0}，在复合域GF((24)2)上的一个元素W的表达形式为W=Whγ1+Wlγ0.其中：υ,γ1,γ0,Wh,Wl∈GF(24).继而推导出W的乘法逆元W-1为

(4)

图2 复合域求逆运算的电路Fig.2 Complex domain inversion operation circuit

从图2中可以看到，GF(28)域乘法逆运算被分解为GF(24)域的常系数平方运算、加法运算、乘法运算和求逆运算.选取不可约多项式I(x)=x4+x+1和参数υ=(1 001)B，则GF(24)域的乘法运算、常系数平方运算和求逆运算分别为式(5)～(7)，加法运算为异或运算.可以看到式(5)、(7)中存在一些重复的公共项，通过公共项消除(Common Subexpression Elimination, CSE)算法消去冗余项进一步减少硬件开销[11]，公共项为f1=(a0⊕a3),f2=(a2⊕a3)，f3=(c2⊕c3).

(5)

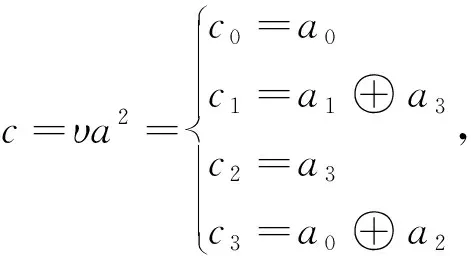
(6)

(7)

此外，式(3)中的同构映射矩阵δ由文献[13]中的算法求得，而δ-1可以和仿射运算中的M矩阵合并为一个8×8的Mδ-1矩阵以减少电路实现时的硬件开销：

(8)

采用Synopsys Design Compiler(K-2015.06)分别对查找表实现、复合域实现2种方案进行了综合，工艺库为TSMC 90 nm CLN90G.表1给出了2种S1-box结构方案的比较(工艺角为SS，温度为125 ℃，电压0.9 V)，面积单位为等效2输入与非门数量.基于复合域的S1-box相比于查找表实现方式节省了约47.0%的硬件开销，在延时方面基于复合域的S1-box架构由于逻辑级数的增加相比查找表实现方式增加了约7.2%.

表1 不同方案实现的S1-box比较

2 基于CLA的模(2311)加法单元

模(2311)(a)所示，由两个31位加法器和一个选择器构成，此外还有两个变种结构分别如图3(b)[14]和图3(c)所示[7]，结构2(图3(b)的结构)省略了选择器而直接使用两个加法器实现，结构3(图3(c)的结构)为了减少延时将加法器并行实现.

图3 模(2311)加法单元的3种结构Fig.3 Three structures of mod (2311) addition unit

本文在结构2的基础上进一步改进模(2311)加法单元结构以进一步降低电路的硬件开销.不难发现模(2311)加法单元的第2个加法器(adder2)仅仅是将前一个加法器的求和值加上1 bit的运算，因此可以将adder2简化为带有进位的单加数加法器，同时考虑到行波进位加法器(Ripple carry adder)的延迟较长，因此采用CLA的结构来设计adder2.CLA中共有3条数据链路，分别为求和、进位传播和进位生成，由于加数B为0，单bitCLA的计算可以简化为式(9)：

(9)

将4个单bit CLA进一步抽象成一个4 bit CLA(CLA-4)(图4(a))，可以更快速地完成计算，其进位生成和进位传播计算如公式(10)所示.

图4 简化后的CLA-4结构和CLA-3结构Fig.4 Simplified CLA-4 structure and CLA-3 structure

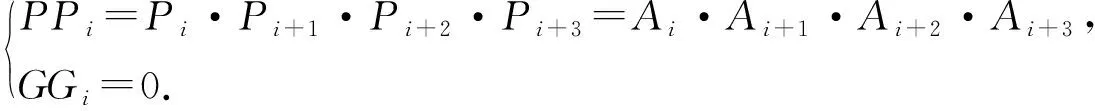
(10)

由于adder2只有31位加数，因此最高位的CLA-4可以简化为CLA-3，如图4(b)所示.将CLA-4和CLA-3组合起来最终得到adder2的整体结构，如图5所示.

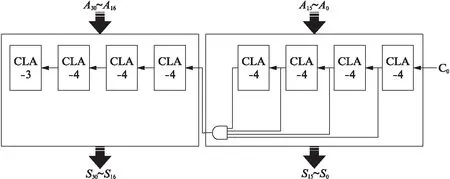
图5 adder2的整体结构Fig.5 The overall structure of adder2

在Design Compiler下(工艺角为SS，温度为125 ℃，电压0.9 V)综合了不同结构的模(2311)加法单元，所提出的基于CLA的模(2311)加法单元与图3中3种结构相比较分别减少了约30.5%、20.2%和32.5%的硬件开销(等效2输入与非门数量)，此外关键路径的延时只比结构3增加了约5.5%，相比结构1和结构2减少了约34.9%和32.1%，具体结果如表2所示.

表2 不同结构的模(231-1)加法单元比较

3 验证与分析

基于以上两部分的改进，本文所提出的面积优化的ZUC算法的整体硬件架构如图6所示.考虑到面积与时序平衡，LFSR部分采用了与文献[8]相似的CSA树型两级流水线结构，CSA树型结构能降低组合逻辑的延时，减少流水级数，从而使用更少的寄存器.本文的ZUC算法架构在初始化阶段每两个时钟周期更新一次LFSR，在工作阶段第1个密钥生成需要两个时钟周期，此后每个时钟周期都生成1个密钥Z，因此每个时钟周期可以处理32 bit数据(即算法吞吐率为32 bit×工作频率).

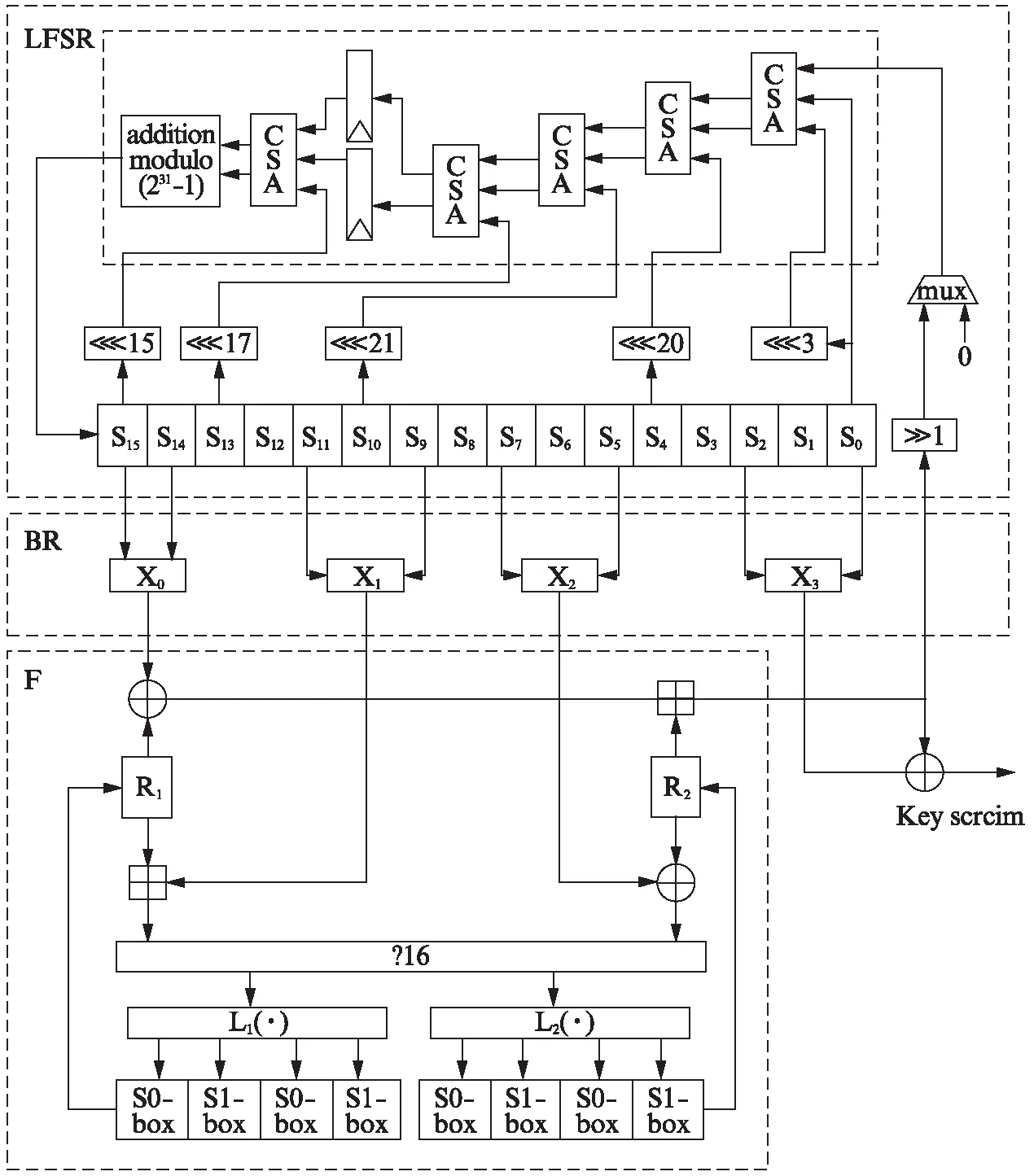
图6 面积优化的ZUC算法硬件架构Fig.6 Hardware architecture of area-optimized ZUC algorithm

采用ZUC算法标准文档中的测试向量(测试向量3)使对所提出的面积优化的ZUC算法的硬件架构进行功能仿真，仿真软件为Modelsim 10.6c，如图7所示仿真结果显示本文方案正确生成了密钥流.

图7 功能仿真结果Fig.7 Functional simulation results

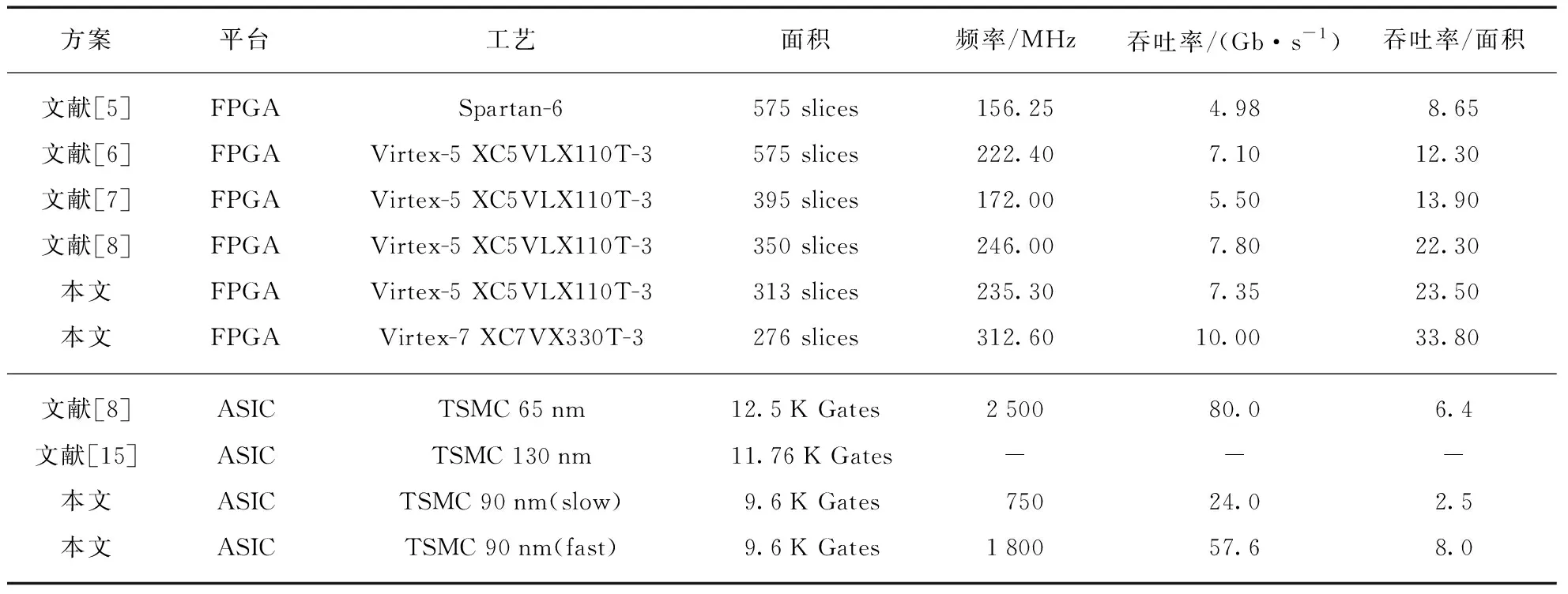
在Xilinx FPGA Virtex-5 XC5VLX110T-3平台(ISE 14.7)、Xilinx FPGA Virtex-7 XC7VX330T-3平台(Vivado 2018.3)和TSMC 90 nm工艺下分别综合实现了所提出的ZUC算法硬件架构，并与目前较优的方案进行比较，结果如表3所示.

表3 本文方案与相关工作在硬件开销及性能表现的比较

Tab.3 Comparison of hardware overhead and performance with related works

方案平台工艺面积频率/MHz吞吐率/(Gb·s-1)吞吐率/面积文献[5]FPGASpartan-6575 slices156.254.988.65文献[6]FPGAVirtex-5 XC5VLX110T-3575 slices222.407.1012.30文献[7]FPGAVirtex-5 XC5VLX110T-3395 slices172.005.5013.90文献[8]FPGAVirtex-5 XC5VLX110T-3350 slices246.007.8022.30本文FPGAVirtex-5 XC5VLX110T-3313 slices235.307.3523.50本文FPGAVirtex-7 XC7VX330T-3276 slices312.6010.0033.80文献[8]ASICTSMC 65nm12.5K Gates250080.06.4文献[15]ASICTSMC 130nm11.76K Gates---本文ASICTSMC 90nm(slow)9.6K Gates75024.02.5本文ASICTSMC 90nm(fast)9.6K Gates180057.68.0

在Xilinx Virtex-5 FPGA平台下，本文所提出的ZUC算法硬件架构与文献[5]、文献[6]、文献[7]、文献[8]的方案相比分别降低了45.6%，45.6%，20.7%，10.6%的硬件开销(以逻辑资源slice为标准)，在频率上仅比文献[8]的降低了4.3%，这是因为随着结构优化电路的关键路径已经从LSFR部分转移到了非线性函数部分(S盒运算)，而本文提出的S盒结构由于逻辑深度的增加引入了部分延时.综合分析各方案的吞吐率与面积情况，本文方案在综合表现上相比于文献[7]提高了5.4%.

在ASIC平台下的ZUC优化实现研究较少，本文所提出的硬件架构与文献[8]、文献[15]的相比较减少了23.2%和18.36%的等效2输入与非门数量，可以看出由于本文提出的改进更针对门级电路进行优化，因此在ASIC平台上的优化效果要更好于FPGA平台.由于不同工艺节点原因，本文方案在频率上与文献[8]有一定差距(文献[15]未给出频率)，本文方案在工艺角为SS，温度为125 ℃，电压0.9 V的条件下频率为750 MHz，而在工艺角为FF、温度为-40 ℃，电压为1.1 V条件下频率能达到1.8 GHz.从吞吐率和面积综合表现来看，本文提出的架构仍然具有较大的优势.

此外，在最新的Xilinx Virtex-7 FPGA平台上实现本文提出的硬件架构，由于FPGA内部基本逻辑结构的升级，硬件开销仅为276 slices，吞吐率达到了10 Gb/s.

4 结 语

针对ZUC密码在嵌入式终端等领域的应用，本文围绕ZUC算法硬件架构的面积优化展开，提出了基于复合域的S1-box设计和基于CLA的模(2311)加法单元设计，并且在此基础上设计了面积优化的ZUC算法的硬件架构.与主流方案相比，本文所提出的架构具有更小的硬件资源开销，同时在性能表现上 接近最好的方案.本文的架构在Virtex-5 FPGA上仅消耗了313个Slices，达到了225.3 MHz的频率；在TSMC 90 nm工艺下硬件开销为9.6 K等效NAND门，在两种平台上较目前主流的方案分别减少了10.6%～45.6%的硬件资源.在最新的Virtex-7 FPGA平台上，本文的ZUC算法架构共消耗了276 Slices硬件资源，吞吐率为10 Gb/s.实验结果表明，所提出的ZUC算法硬件架构能同时兼顾硬件资源开销少与性能表现好的优点.