四旋翼无人机的参数辨识方法

何毅杰，艾剑良

(复旦大学 航空航天系，上海 200433)

目前对多旋翼(Multi rotor)无人机(Unmanned Aerial Vehicle， UAV)的控制的研究是一个热点．多旋翼无人机具有机动性好、便携、廉价等特点，可以承担多样化的飞行任务.在执行某些特殊的飞行任务时，无人机的质量、重心、惯性矩会发生变化，这会降低无人机控制系统的稳定性，甚至导致控制系统发散．对动力学参数的辨识可以帮助调整控制系统的参数，从而适应这种变化．在辨识的过程中，状态信号所含的噪声对辨识结果的精确度有着重要的影响．为了控制小型无人机的成本，所使用的廉价传感器往往不够精确，噪声比较大.为了保证参数辨识的精确度，需要合理地降低噪声的影响．本文所用的互补滤波器(Complementary filter)将高频噪声和低频噪声结合，最大程度地消除误差、保留有效数据．另外，本文注意到，参数辨识模型中的状态向量含有输出信号的微分信号，而用一步差分近似求得的微分信号在精度上有先天的不足，故本文采用了跟踪微分器(Tracking Differentiator， TD)来更精确地取得输出信号的微分信号．仿真结果表明，采用这些方法可以比较好地提高参数辨识的精确度.

1 参数辨识的基本概念

参数辨识就是假设系统输入u(t)和输出y(t)已知[1]，求系统的传递函数G(s)，即通过采集系统的输入输出数据，研究确定系统数学模型的理论和方法．一个连续时间的动态系统一般可用高阶微分方程来描述(离散系统用差分方程来描述)，通过引进一些中间变量(状态变量)，可以化为一些1阶微分方程(差分方程)，这个表示系统输入输出关系的方程组称为状态空间模型.

系统辨识的4个要素是数据、模型类、准则、优化方法.具体来说，就是基于一种准则，采用某种优化方法，在一类模型中找到与数据最吻合的模型.无人机动力学模型以物理定律为依据，因此是先验的.需要辨识的参数包括: 无人机的转动惯量、质量、重心的位置，旋翼的升力系数、阻力系数.考虑到飞行过程中参数变化的情况，故采用在线辨识的形式.

2 四旋翼无人机的动力学模型

为了辨识无人机的动力学参数，首先要建立起四旋翼无人机的动力学模型.

先建立机体坐标系，确定原点位置及各个坐标轴的方向: 以重心G为原点，机头方向为x轴，垂直机身向下为z轴，侧向为y轴，如图1所示．然后可以据此定义欧拉角(即无人机各姿态角)的符号: 俯仰角θ以抬头为正，偏航角ψ以向右为正，滚转角φ以向右为正.

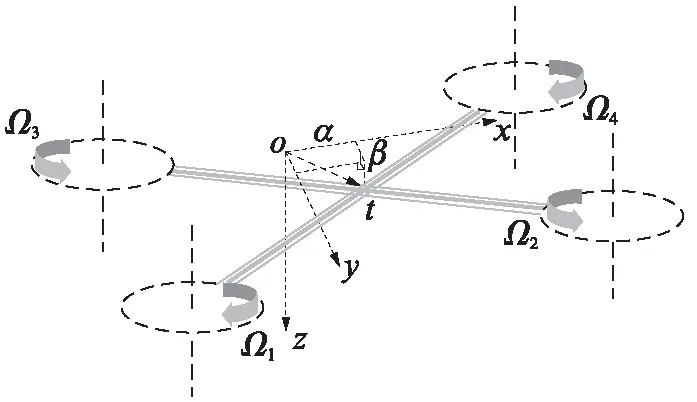
图1 四旋翼无人机机体坐标系的示意图Fig.1 Schematic diagram of body coordinate system of quadrotor UAV

基于机体坐标系的建立方法，推导出6自由度动力学方程．将无人机认为刚体，忽略弹性形变的影响.

根据质心运动定理[2]:

(1)

惯性系下，质心的运动方程为

(2)

质心的动量矩定理[2]:

(3)

(4)

(5)

两个坐标系下角速度的坐标变换公式为

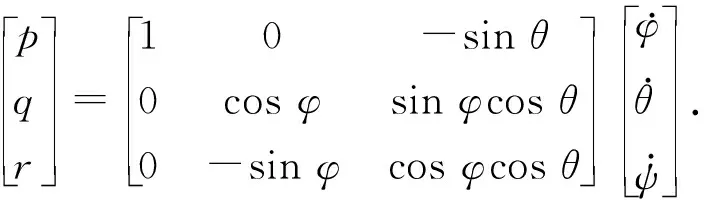
(6)

令式(6)两边对时间t求导，得:

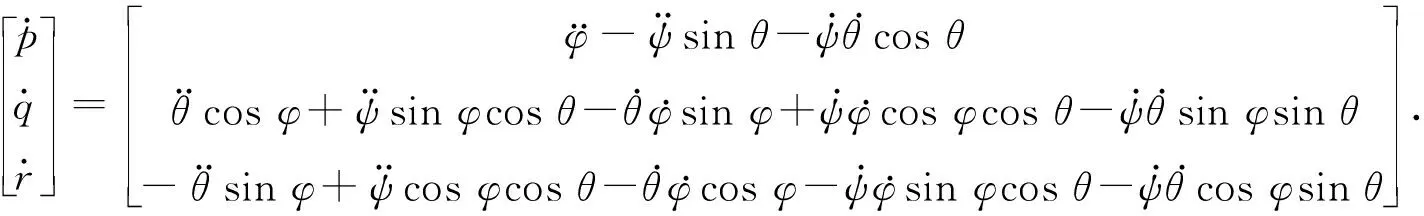
(7)

机体坐标系下的合外力矩表达式:

(8)

其中：kT是单个旋翼的拉力系数；kM是单个旋翼的力矩系数.

以上各式就是无人机一般运动的全部动力学方程．本模型忽略空气阻力的影响．α，β如图1所示，实际上是飞机的几何中心t在以重心G为原点的机体坐标系中的坐标，可以表示重心的位置．z轴坐标与动力学模型无关，不需辨识.

3 辨识算法

第2节建立的6自由度模型是一个线性参数系统，意味着它可以写成如下形式:

y(t)=φ(t)θ+ξ(t).

(9)

其中:y(t)是系统输出；ξ(t)是干扰噪声；φ(t)是由系统的输入输出数据构成的状态向量；θ是待辨识的参数向量．这样的形式称为最小二乘格式，因为这种形式的系统易于被最小二乘法辨识[1].最小二乘法作为一种凸优化方法[3]，最大的优点就是求得的极小点必定是全局极小点，不会陷入局部最优．因此，线性参数系统优先选择使用最小二乘法来辨识[4].

最小二乘法的基本形式如下: 令

(10)

优化目标是极小化F(θ).假设fi(θ)=φiθ-yi,i=1,2，…,m，则

(11)

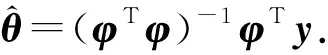
在实际应用中，飞行器的模型参数不会保持不变．为了应对这种变化，参数辨识和控制需要同时进行，因此要对飞行器的参数做在线辨识，故本文采用最小二乘法的递推形式:

(12)

根据式(5)和(8),可以将动力学模型改写成最小二乘格式:

(13)

根据式(13)，即可应用递推最小二乘法来辨识参数.

4 跟踪微分器

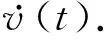
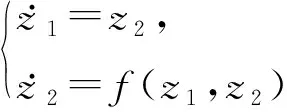
适当选取函数f，令

(14)

跟踪微分器的输出信号本质上是对输入信号的微分的一种近似．相对于差分算法，跟踪微分器能够以产生少量的偏差为代价，抑制噪声的放大效应．此外，与差分算法相比，跟踪微分器对突变信号的跟踪比较平滑，误差比较小．跟踪微分器的效果主要与R的取值有关．R太大，噪声的放大效应反而增强；R太小，则跟踪信号的偏差过大．根据输入信号中所含噪声的方差大小，为R取到恰当的值，则x1可以准确地跟踪输入信号，x2可以准确地跟踪输入信号的微分信号，并且相对于差分算法，微分器对噪声的放大效应得到了抑制.

5 互补滤波算法

测量多旋翼无人机飞行状态的元件主要包括陀螺仪和加速度计．陀螺仪输出姿态角的角速度信号，而加速度计输出飞机的加速度信号，然后通过积分得到姿态角、位移和速度信号．由于测量仪器本身的误差、外部环境的扰动误差以及模型误差，这些数据不能准确反映无人机的真实运动状态，由此造成的测量结果和真实值的差异称为噪声．其中，姿态角及其1阶、2阶微分信号的噪声对参数辨识的精确度影响最大.

从实验的结果来看，加速度计产生的是高频噪声，而陀螺仪产生的是低频噪声．由于加速度计的测量原理，它的测量值与姿态角有换算关系，因此，可以用加速度计的信号来修正陀螺仪的信号，这就是互补滤波器[5].

互补滤波器由一个低通滤波器和一个高通滤波器组成，且它们的传递函数和为1.这样的滤波器可以确保有用的信息不会损失，所以又称作无损滤波器[6].

互补滤波器的构造如下[7-8]:

假设有两个信号y1=x+μ1，y2=x+μ2，其中：x为信号内容；μ1，μ2为噪声．构造两个滤波器G1(s)，G2(s)，且令G1(s)+G2(s)=1，则

(15)

其中：Y1(s)，Y2(s)，X(s),μ1(s),μ2(s)分别是y1,y2,x,μ1,μ2经拉氏变换后的表达式.

(16)

则

(17)

分析滤波器的幅频特性，由于G1(s)和G2(s)分别是高通和低通滤波器，而截止频率都是kp(单位为rad/s)，因此适合对一组分别带低频噪声和高频噪声的信号进行滤波．因为G1(s)作用于陀螺仪信号(低频噪声)，而G2(s)作用于加速度计信号(高频噪声)，所以这样的结构是合理的.

在参数辨识中，需要用到姿态角和它的1阶、2阶微分信号．由于微分器对噪声在频域上的低频部分(Ω<1 rad/s)有抑制效应，高频部分(Ω>1 rad/s)有放大效应，而积分器则相反．因此，对于姿态角信号的滤波，应当偏向高频部分，即让kp更大，而对于1阶、2阶微分的滤波，应当偏向低频部分，即让kp更小．合理调整kp的值，可以在高、低频噪声之间取得平衡，有效地降低噪声的方差，取得最佳的滤波效果.

6 计算实例

本算例运用Simulink建立如上文所描述的四旋翼无人机动力学模型[9]，配置微分器和滤波器，并为待辨识的各个参数赋值，所赋的值综合考虑了3D建模软件的计算结果和实际测量的无人机参数．Simulink仿真模块的示意图如图2所示.

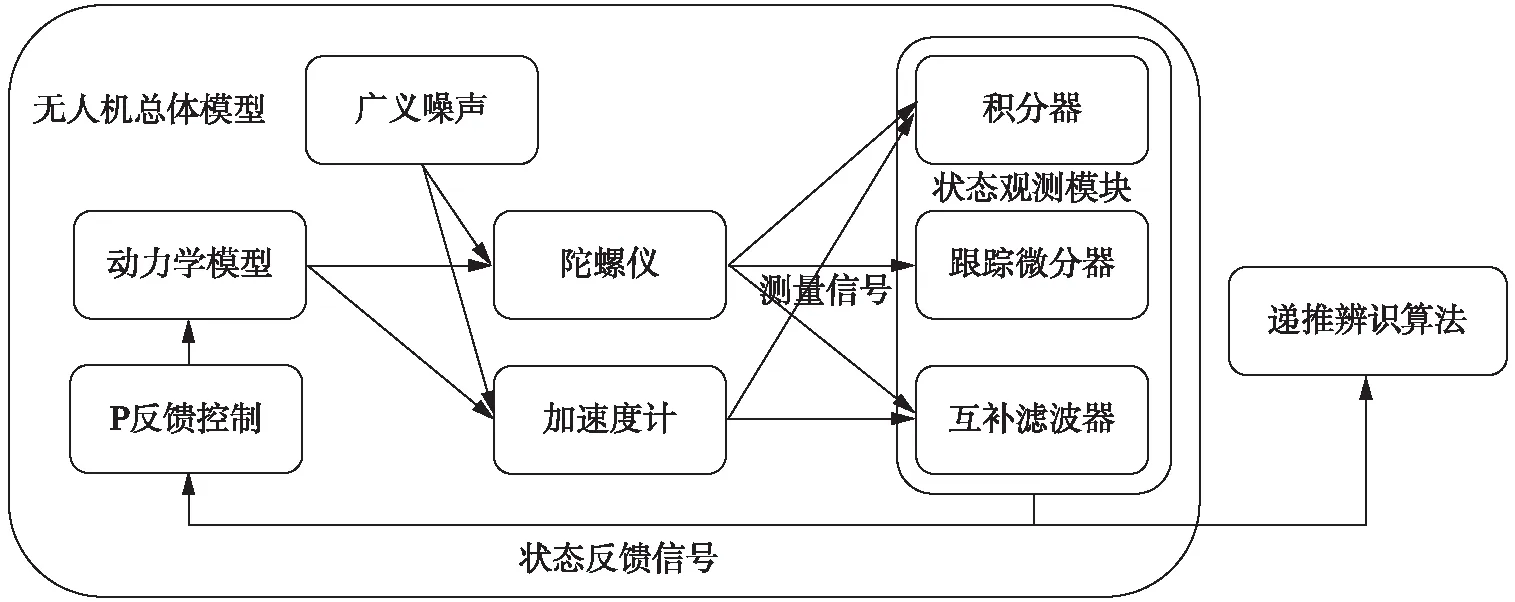
图2 Simulink仿真模块的示意图Fig.2 Schematic diagram of Simulink simulation module

设计输入使得飞机做出机动动作，并给输出数据加上噪声，然后用递推最小二乘法进行估算．计算仿真中的有色噪声可以将白噪声通过一个成形滤波器得到．为尽量真实地还原噪声，将白噪声的采样频率设置为10 000 Hz，成形滤波器的z变换式如下:

可以计算出有色噪声的均值为0.00，均方差为0.02.

配置跟踪微分器的参数．令R取到合适的值，那么微分器的输出信号趋近于输入信号的微分信号，并且抑制了噪声的放大效应．而a应当接近1但不为1，使得微分器是非线性的．为降低微分器的超调，根据经验公式，令b=3.1(a-0.5)+1.17.因此取参数a=1.75，b=5.045，R=50 000.

配置互补滤波器的参数．对于姿态角信号，以高频噪声为主，取较大的kp，令kp=5；对于1阶、2阶微分信号，高频噪声经由微分器放大，不应再用来修正低频噪声，故令kp=0.

参数辨识不必对飞行轨迹有过高的要求，而是要尽量激发出飞行器的各种模态，使得所有待辨识参数的相关信息都包含在输出数据当中．本文采取“多模态、大幅度”的原则来设计飞行动作，并采用PID(Proportional integral derivative)状态反馈控制器进行控制．为加大震荡幅度，只保留PID控制器的比例环节，并且使得比例系数k较大，取k=100.采样频率为20 Hz，总仿真时间为20 s.

为了最大限度地降低噪声的影响，为参数辨识设计了3种典型模态，分别对应3次仿真飞行，得到3组仿真数据．具体如下:

模态1 前10 s飞机上升到5 m高度并悬停，后10 s飞机以3 m/s的速度向右飞行.

模态2 前10 s飞机上升到5 m高度并悬停，后10 s飞机以3 m/s的速度向前飞行.

模态3 前10 s飞机上升到5 m高度并悬停，后10 s飞机绕z轴旋转4周.

各组飞行仿真的数据如图3～图8所示.

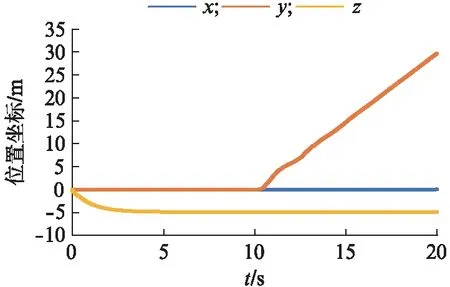
图3 模态1无人机的位置变化Fig.3 Location change of UAV in mode 1

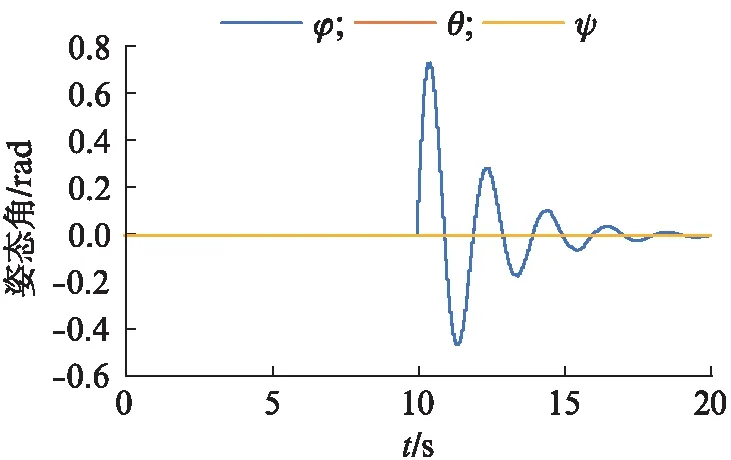
图4 模态1无人机的姿态角变化Fig.4 Attitude angle change of UAV in mode 1

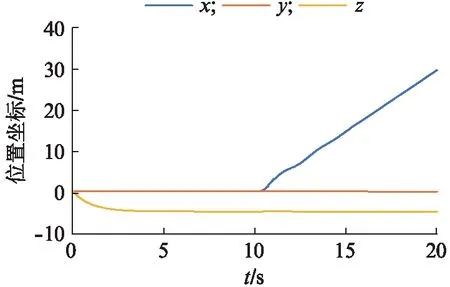
图5 模态2无人机的位置变化Fig.5 Location change of UAV in mode 2

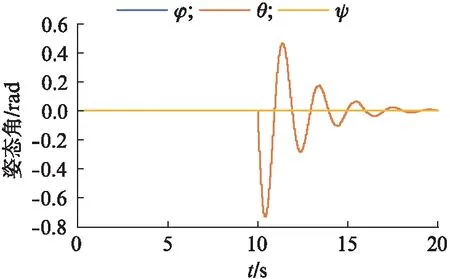
图6 模态2无人机的姿态角变化Fig.6 Attitude angle change of UAV in mode 2

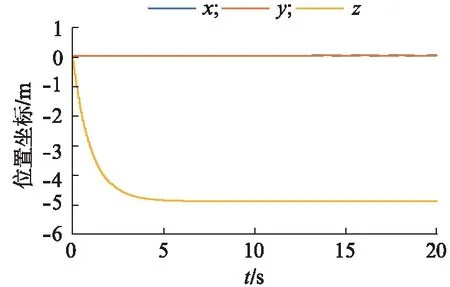
图7 模态3无人机的位置变化Fig.7 Location change of UAV in mode 3

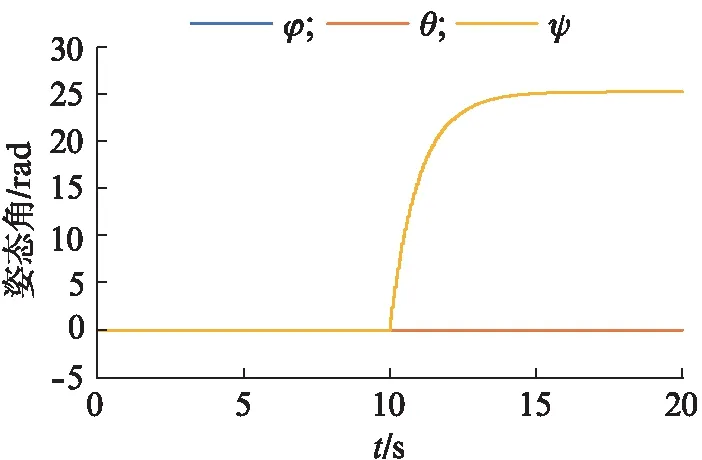
图8 模态3无人机的姿态角变化Fig.8 Attitude angle change of UAV in mode 3

在典型模态下，各个参数与输入输出数据的相关性有大小之分，此时各个参数的辨识准确度受噪声的影响也各不相同．相关性越大，辨识准确度受噪声的影响就越小．为了尽量准确地辨识出所有参数，我们采取分步辨识的方法:

设已辨识的参数向量为θd，待辨识的参数向量为θr，那么可以将参数模型式(9)改写成:

y=φdθd+φrθr.

(18)

(19)

对式(19)应用递推最小二乘法，即可辨识出余下的参数.

具体辨识步骤如下:

第1步 在模态1的数据中辨识Ix，Ixy，α，β，kT，在模态2的数据中辨识Iy，在模态3的数据中辨识Iyz，Ixz；

第2步 在模态2的数据中辨识kM；

第3步 在模态3的数据中辨识Iz.

辨识结果如表1所示.

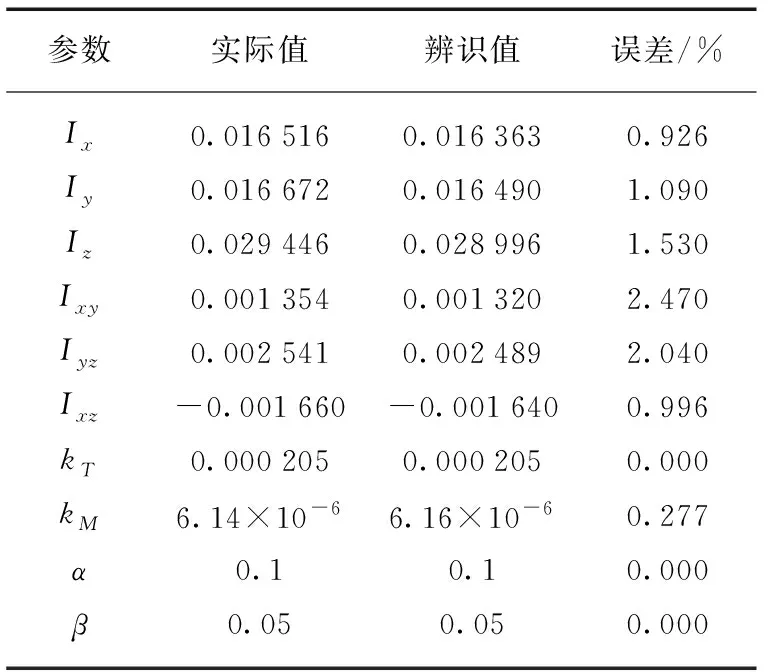
表1 参数辨识值与所赋实际值的对照

7 结 语

从上述仿真结果可以看到，所较小．其中Ixy，Iyz的误差略微偏大．参数辨识结果的误差应当与该参数在线性参数模型中对姿态角及其微分信号所带的噪声相对敏感有关．仿真结果表明，对于多旋翼无人机的参数辨识而言，如何处理姿态角和其1阶、2阶微分信号及所含的噪声，对参数辨识的精确度具有显著的影响，故而参数辨识对传感器的精度要求很高．与此同时，运用包括跟踪微分器、互补滤波器在内的方法处理姿态角和其1阶、2阶微分信号及所含的噪声，可以有效地提高参数辨识的精确度．另外，研究注意到，在噪声不可避免的情况下，对输入和输出信号的选取也对参数辨识的精确度有很大的影响．一般来说，设计辨识飞行实验的时候要尽量避免运动姿态的耦合，并采集运动幅度较大时段的飞行数据，这对参数辨识非常有利，可大大降低噪声的影响．在未来的研究中，可以考虑将有色噪声的成形滤波器参数也作为辨识的对象，将噪声与信号分离开来，从而进一步提高参数辨识的精确度．