基于数据的K均值理论及其应用

杨 金,陈 林,周 强,陈建勋

(1.重庆交通大学数学与统计学院,重庆 400074)(2.重庆南开中学,重庆 400074)

本世纪初,我国直接采用欧洲的NEDC(新标欧洲循环测试)行驶工况对汽车产品能耗/排放的认证,有效促进了汽车节能减排和技术的发展[1]. 但随着我国汽车保有量的迅速增长,交通状况的逐渐变化,继续以NEDC工况为基准所优化标定的汽车,其法规认证结果与使用过程中的实际油耗量相比较,差距越来越大[2]. 因而,制定能反映我国实际道路行驶状况的行驶工况迫在眉睫. 本文主要采集了某城市同一辆轻型汽车在不同时间段共21 d所获得的数据,针对人工筛选的不足,首先对数据时间不连续、加、减速度异常、长期停车、长时间堵车、怠速4种情况的异常数据进行处理,然后对运动学片段进行划分,再通过主成分分析方法对车辆行驶工况的特征参数进行处理,根据选出的特征参数利用K-均值聚类分析方法将所有代表性运动学片段按低速、中速和高速进行聚类,最终拟合成汽车行驶工况的全过程,由此建立了某市同一辆轻型汽车合理的行驶工况,其设计方案简单合理,具有很好的实用价值.

1 预备知识

由于GPS信号不良、数据采集设备故障、堵车等状况造成部分无效和异常数据,必须对无效和异常数据进行数据处理. 本文主要考虑数据时间不连续、加、减速度异常、长期停车、长时间堵车、怠速4种情况的异常数据,接下来我们给出上述4种情况的定义及其处理方式.

1.1 数据处理

为使采集的数据更加全面,本文利用可插入GPRS手机卡和SD储存卡的记录仪采集某城市同一轻型车不同时间段在实际道路行驶的数据. 采样频率为1 Hz,将采集到的GPS车速、X轴加速度、Y轴加速度、Z轴加速度、发动机转速、扭矩百分比、瞬时油耗、油门踏板开度、空燃比、发动机负荷百分比、进气流量等数据从SD卡中导出.

数据时间不连续:往往是由汽车行驶过程中GPS信号丢失导致的. 由于数据以秒为单位,且数据量往往是几十万甚至上百万,人工筛选工作量过于巨大,因此选择编写计算机程序筛选出非连续数据. 此时需要对非连续数据进行定义及处理,具体定义及处理方式如下:

令ti、ti+1为相邻两时间点且ti1,则定义ti、ti+1为时间数据不连续时刻.此时,包含ti时刻的连续行驶片段与包含ti+1时刻的连续行驶片段时间上不连续,如果删除ti或ti+1时间点得到的数据集依然是不连续的,那么需要对这个时间点附近的数据进行处理.找到距离ti时间最近且GPS车速为0的时间点t′,及距离ti+1时间最近且GPS车速为0的时间点t″,判断,vi、vi+1的速度,有以下4种情况:

若vi=vi+1=0,根据运动学片段的定义,认为[t′,ti]、[ti+1,t″]时间段车辆行驶数据可以构成一个完整的运动学片段,保留[t′,ti]与[ti+1,t″]时间段的车辆行驶数据;

若vi=0且vi+1≠0,则[t′,ti]时间段车辆行驶数据可以构成一个完整的运动学片段,保留[t′,ti]时间段的车辆行驶数据,而[ti+1,t″]时间段车辆行驶数据无法构成一个完整的运动学片段,删除[ti+1,t″]时间段的车辆行驶数据;

若vi≠0且vi+1=0,则[t′,ti]时间段车辆行驶数据无法构成一个完整的运动学片段,删除[t′,ti]时间段的车辆行驶数据,而[ti+1,t″]时间段车辆行驶数据可以构成一个完整的运动学片段,保留[ti+1,t″]时间段的车辆行驶数据;

若vi≠0且vi+1≠0,则[t′,ti]与[ti+1,t″]时间段车辆行驶数据无法构成一个完整的运动学片段,删除[t′,t″]时间段的车辆行驶数据,删除[t′,t″]所有数据后,包含t′时刻的连续行驶片段与包含t″时刻的连续行驶片段虽然时间上不连续,但是保证了每部分片段之间时间的连续性,每部分片段可以认为是一个运动学片段.

加、减速度异常:汽车行驶过程中,对于一辆普通轿车,一般情况下:0～100 km/h的加速时间大于7 s,紧急刹车最大减速度在7.5 m/s2～8.0 m/s2.由于采集的数据中并不能直接得到加速度,因此首先测算每个时刻的加速度.

加速度的定义为:单位时间内速度改变程度的矢量.若动点的速度vi经(ti+1-ti)s后变成vi+1,加速度计算公式如下:

(1)

考虑到已知数据是以秒为单位测算车辆的速度,本文加速度测算公式如下:

(2)

将测算的加速度与普通轿车一般情况下加、减速度做比较,根据公式(1),最大加速度为4 m/s2,最大减速度为7.5 m/s2,超过则为加、减速度异常情况.

按照公式(2)测算所有时刻的加速度,将各个时刻的加或减速度与最大加速度为4 m/s2和最大减速度比较,判断该时刻的加或减速度是否存在问题,具体定义及处理方式如下:

令ti时刻的加速度为ai,vi代表ti时刻的速度,若ai>4 m/s2、ai<-7.5 m/s2,则定义ti时刻为加或减速度异常的数据时刻,如果删除ti时刻的数据,必然会导致原本包含ti时刻的车辆连续行驶片段不连续,因此需要对这部分数据进行处理.

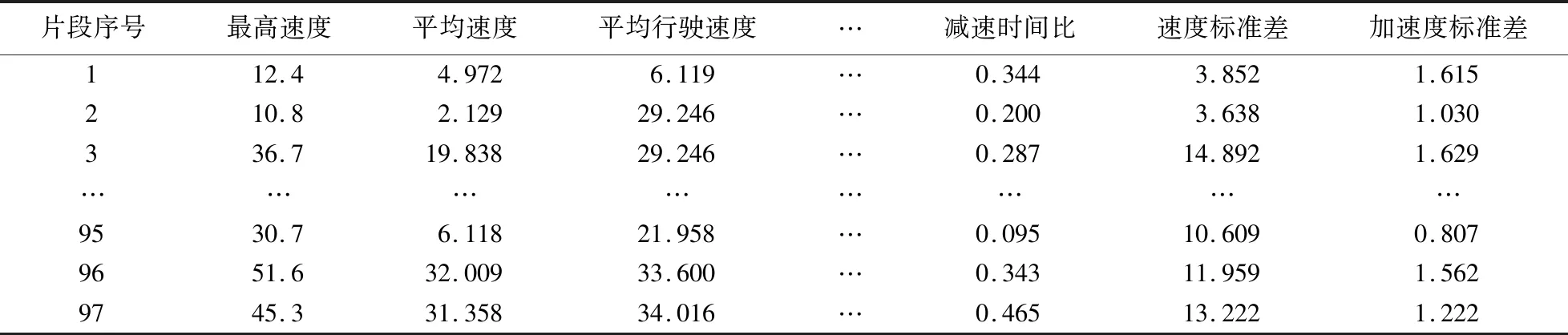
若vi≠0,找到距离ti时间最近且GPS车速为0的时间点t′、t″,且t′

若vi=0,找到距离ti时间最近且GPS车速为0的时间点t′,且t′>ti,删除[ti,t′]时间段的车辆行驶数据,即完成了汽车突然加、减速度产生的异常数据的处理,删除[ti,t′]的所有数据后,包含ti时刻的车辆连续行驶片段与包含t′时刻的车辆连续行驶片段虽然时间上不连续,但是保证每部分片段之间时间的连续性,每部分片段可以被认为是一个运动学片段.

长期停车:定义vi=0的连续时刻的累计时间超过180 s为长期停车状态,将所有vi=0的连续时间区间通过计算机语言筛选出来,并判断累计时间是否超过180 s,若[t′,t″]为连续时间vi=0区间,则累计时间计算方式如下:

cumulativetime=(t″-t′)+1.

(3)

长期停车产生的异常数据具体定义及处理方式如下:令通过MATLAB编程语言筛选出vi=0的连续时间区间为[t′,t″],根据公式(3)计算vi=0的连续时刻的累计时间,若cumulativetime>180 s,删除[t′,t″]时间段的车辆行驶数据,即完成了长期停车产生的异常数据处理.

堵车、怠速:由于长时间堵车、断断续续低速行驶通常按怠速情况处理,即vi=0的情况,因此长时间堵车、断断续续低速行驶时间超过180 s,可理解为长期停车状态,长期停车为异常情况,需要对这部分数据进行处理.

具体定义及处理方式:通过MATLAB编程语言筛选出vi≠0的连续时间范围:{ti,ti+1,ti+2,…,t′},其速度范:{vi,vi+1,vi+2,…,v′},若max{vi,vi+1,vi+2,…,v′}<10 km/h,则定义[ti,t′]这段时间为长时间堵车、断断续续低速行驶时间,根据公式(3)计算,若cumulativetime>180 s,删除[ti,t′]时间段的车辆行驶数据,即完成了长期停车产生的异常数据处理.

1.2 运动学片段划分

运动学片段是指汽车从怠速状态开始至下一个怠速状态开始之间的车速区间[3].本文划分运动学片段的标准是:

1.从汽车速度为零的状态开始,到下个时间为零的状态结束;

2.全过程持续时间必须是连续的,且超过50 s;

3. 过程中的最大速度大于10 km/h.

将上述3个条件用MATLAB软件对筛除异常后的数据进行运动学片段的划分,我们共得到了1 648个运动学片段. 从这1 648个运动学片段中随机选出4段数据绘制其速度-时间图,如图1所示,并将第一节运动学片段的速度-时间图提取出来. 如图2所示.

图1 4节运动学片段的速度-时间图Fig.1 Velocity-time diagram of four segments of kinematics

图2 运动学片段的速度-时间图Fig.2 Velocity-time diagram of kinematic segments

从图1可以看出,这4节运动学片段的开头和结尾处的速度为0,无间断区间,最大速度均大于 10 km/h,因此,这4节运动学片段均满足上述划分运动学片段的3个标准,由此可以验证编写的MATLAB代码的有效性.由图2,速度为0的运行状态即怠速状态,速度随着时间的增加而增加的运行状态为加速状态,速度随着时间的增加而减少的运行状态为减速状态,速度随着时间的增加不产生较大变化的状态为匀速状态.

2 算法原理及应用

前面已经介绍了数据处理方法和运动学片段的划分,下面我们将引入本文要用到的主成分分析方法和K-均值聚类方法的算法原理.

2.1 算法原理

汽车行驶工况是描述汽车行驶速度与时间的曲线[4].初步选择以下11个与速度相关的参数作为汽车运行特征参数:最高速度vmax;平均速度vm;平均行驶速度(不含怠速)vmr;平均加速度aa;平均减速度ac;速度标准差vsd;加速度标准差asd;加速时间比例Pa;等速时间比例Pb;减速时间比例Pc;怠速时间比例Pd.针对选定的11个特征参数,我们选用主成分分析法得到对行驶工况影响最大的几个因素[5-6],主要步骤如下:

第一步,对11个特征参数进行主成分分析[7-8],得到较大影响的特征参数.

上述11个特征参数和所有区间片段的参数矩阵如下:

(4)

式中,xii(i=1,2,…,r,j=1,2,…,s)是第i个区间片段的第j个参数;r是所有区间片段数;s是所有特征参数个数.

对参数矩阵X进行标准化,得到矩阵Y如下:

(5)

式中,

(6)

(7)

(8)

由矩阵Y计算协方差矩阵Z,其定义如下:

(9)

式中,

(10)

(11)

由矩阵X得到相关矩阵G,定义如下:

(12)

式中,

(13)

用λi表示矩阵G的特征值,λ1≥λ2≥…≥λn≥0, 相应正交化特征向量如下:

(14)

用Ri表示第i个主成分的贡献率,定义如下:

(15)

式中,贡献率Ri越大,表示该主成分i所表达的信息越多.

用LRθ表示前θ个特征值的贡献率之和,定义如下:

(16)

式中,如果LRi≥80%,前θ个特征值就能满足应用需要,即每个区间片段有θ个主成分.由此可以得到θ个对车辆行驶工况有较大影响的特征参数.

第二步,将主成分分析确定的θ个特征参数用于聚类分析中,用于评价片段之间的相关程度[9-10].

相关程度通过相关系数衡量,相关系数的定义如下:

(17)

(18)

通过公式(17)-(18)可对所有代表性运动学片段进行聚类[11-12],按照低速、中速、高速3类运行状态将所有代表性运动学片段归为3类.

第三步,对于3类运行状态提取的不同数量运动学片段条数进行数据拟合.

本文构建的车辆行驶工况时长在1 200 s～1 300 s之间,可通过各类总运行时间在总体数据时间中所占的时间比确定各类最终拟合工况所占的时间,定义如下:

(19)

式中,Tk为第k类在最终拟合的车辆行驶工况图所占时间;Tall为所有带变形运动学片段的持续时间;Tduringtime为要构建的车辆行驶工况的持续时间;Nk为第k类运动学片段的总条数;Tki为第k类中第i条运动学片段的运行时间.由公式(19)可分别从3类运行状态下提取不同数量的运动学片段条数,最后拟合成车辆行驶工况图.

2.2 算法案例

从预处理后的数据中,按时间长度在1 100 s～1 400 s之间的连续行驶区间将所有连续行驶区间提取出来,一共提取了11个区间,并对这11个区间按照运动学片段的定义划出了97个代表性运动学片段.

根据选出的11个特征参数计算97个运动学片段的部分特征参数值(表1).

表1 97个运动学片段的特征参数Table 1 Characteristic parameters of 97 kinematic segments

根据表1的数据进行主成分分析,得到11个特征参数即11个主成分的特征值、贡献率及累计贡献率数据表,以及主成分载荷矩阵表,如表2、3所示.

表2 各个主成分的特征值、贡献率及累计贡献率Table 2 Eigenvalues,contribution rate and cumulative contribution rate of each principal component

从表2看出,前3个主成分累计贡献率超过80%,因此选取前3个主成分进行分析,通过SPSS软件分析,可得到前3个主成分的载荷矩阵.

从表3可以看出:

表3 主成分载荷矩阵表Table 3 Principal component load matrix

(1)第一类主成分主要反映平均速度、最高速度、平均行驶速度;

(2)第二类主要反映加速度标准差;

(3)第三类主要反映速度标准差.

因此根据主成分分析选出的特征参数:平均速度、最高速度、平均行驶速度、加速度标准差、平均加速这5个特征参数进行聚类分析,将所有代表性运动学片段按照低速、中速、高速进行聚类,最终聚类中心对比如图3所示.

图3 聚类中心对比图Fig 3 Comparison of cluster centers

从图3中可以看出,第Ⅰ类片段的加速比例较高,反映了车辆在畅通无阻的道路上的行驶情况,可以定为高速片段;第Ⅱ类片段的怠速比例较大,反映了车辆在拥挤的道路上行驶,可以定为低速片段;第Ⅲ类片段的匀速比例较大,反映了车辆稳定形式的状态,可以定为中速片段.

通过SPSS软件分析,可得到K均值聚类分析的聚类成员列表,如表4所示.

表4 K均值聚类分析的聚类成员列表Table 4 List of cluster members of K-means cluster analysis

从表4可以看出,97个运动学片段被分成3类,第Ⅰ类包括了16个运动学片段,第Ⅱ类包括了32个运动学片段,第Ⅲ类包含了49个运动学片段. 公式(19)计算取整后,可获得2条第Ⅰ类高速片段,4条第Ⅱ类低速片段,5条第Ⅲ类中速片段,最后拟合成持续时间为1 207 s的车辆行驶工况图,如图4所示. 在0～272 s之间为车辆低速行驶状态,且低速状态的车速低于24.6 km/h;在272 s～930 s之间为车辆中速行驶状态,且中速行驶状态的车速普遍处于24 km/h～43.7 km/h;在930 s～1 207 s之间为车辆高速行驶状态,且高速行驶状态车速最高达到了64.4 km/h.

图4 构建的汽车工况速度-时间图Fig.4 Constructed speed-time diagram of vehicle working condition

3 结论

本文通过采集某城市同一辆轻型汽车在不同时间段共21 s所获得的数据,主要介绍了如何通过处理大量的汽车行驶数据来得到汽车运动学原理. 首先对数据时间不连续、加减速度异常、长期停车、长时间堵车和怠速4种情况的异常数据进行处理,然后运用MATLAB软件对筛除异常后的数据进行运动学片段的划分,并从中取出具有代表性的运动学片段,再利用主成分分析方法求出对车辆行驶工况有较大影响的特征参数,用得到的特征参数求出用于评价片段之间的相关程度的片段间的相关系数和片段之间的距离,再使用K-均值聚类方法对所有代表性运动片段进行聚类分析,将所有运动学片段按照低速、中速、高速的运动状态分为3类,并得到了聚类中心对比图. 最后根据K-均值聚类分析的聚类成员对3类运行状态提取的不同数量运动学片段条数进行数据拟合,最终拟合成包含低速、中速和高速3种运动状态的汽车行驶速度与时间的曲线,即持续时间为1 207 s的汽车行驶工况图,由此得到汽车运动学的数学原理. 本文通过对汽车运动学数学原理的探索,为相关部门制定出反应我国实际情况的汽车行驶工况提供理论依据,为车辆设计的动力匹配、提高发动机的燃油消耗率、有效降低尾气排放提供参考,对我国汽车工业的发展具有重要意义.