从一道八省联考试题探析导数与三角函数交汇题型的求解方法

郑文杰 廖小莲

(湖南省娄底市湖南人文科技学院数学与金融学院 417000)

导数与三角函数相结合的题目是属于比较创新的题型，而在八省联考当中就出现了，有人做了有关高考三角函数的命题分析及规律，也有人探究了高考导数的应用，但是存在关于导数与三角函数相结合的这方面的研究确实比较少.

一、以三角函数为载体的恒成立问题

例题1(2021年八省联考，第22题)已知函数f(x)=ex-sinx-cosx，g(x)=ex+sinx+cosx.

(2)若g(x)≥2+ax，求a.

图1

(2)已知g(x)≥2+ax,且g(x)=ex+sinx+cosx，则ex+sinx+cosx≥2+ax.

移向可得：ex+sinx+cosx-2-ax≥0，设φ(x)=ex+sinx+cosx-2-ax，则φ′(x)=ex+cosx-sinx-a，φ(0)=0，由于在定义域R中满足φ(x)≥0恒成立,且φ(0)=0，即x=0是φ(x)的零点也是φ(x)的极小值点，所以φ′(0)=2-a=0即a=2,φ′(x)=ex+cosx-sinx-2的图像如图2所示.

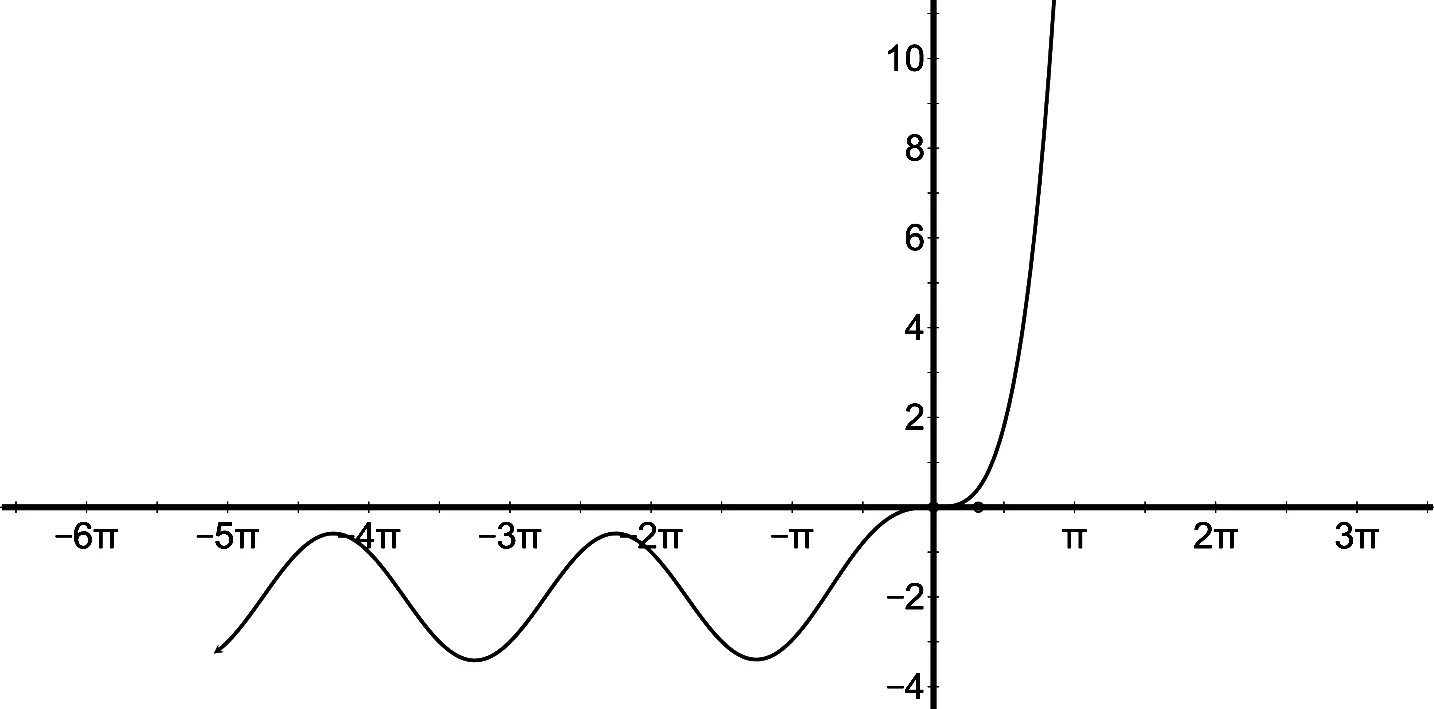
图2

反过来验证：当a=2时φ(x)≥0恒成立，即ex[1+(sinx+cosx-2x-2)e-x]≥0

设F(x)=(sinx+cosx-2x-2)e-x,即证明F(x)≥-1

F′(x)=(cosx-sinx-2)e-x-(sinx+cosx-2x-2)e-x=2e-x(x-sinx)，设M(x)=x-sinx，即M′(x)=1-cosx,由于cosx≤1所以M′(x)=1-cosx≥0，所以M(x)在R上单调递增，又因为M(0)=0,即在(-∞,0)上M(x)<0,即F′(x)<0;在(0,+∞)上M(x)>0,F′(x)>0，所以F(x)在(-∞,0)上单调递减;(0,+∞)上单调递增.所以F(x)≥F(0)=-1；所以(sinx+cosx-2x-2)e-x≥-1；即ex+sinx+cosx-2-2x≥0；综上所述:a=2.

总结①当遇到指数函数与三角函数都存在时,一定要学会将它们两个绑定在一起，即相乘的关系;②对于导数与三角函数的恒成立问题，通常都是考查 “端点”效应，而这里的“端点”可能是区间端点也有可能是整个函数的对称点.

二、以三角函数为载体的不等式证明问题

例题2(2021年八省联考，第22题)：已知函数f(x)=ex-sinx-cosx，g(x)=ex+sinx+cosx.

(2)若g(x)≥2+ax，求a.

在这只解答的第二问，第一问在类别一已经全部解答了.

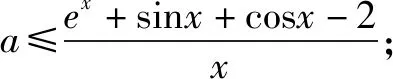
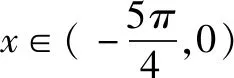
总结在导数中的不等式证明中碰见含参数的不等式证明，我们首先参变分离，将不熟悉的题目要转换成我们熟悉的东西.