基于扇形趋利果蝇优化算法改进的FS-K聚类算法*

曹珍贯, 杨 逊, 吕旻姝, 朱靖雯

(安徽理工大学 电气与信息工程学院， 安徽 淮南 232001)

0 引 言

果蝇算法(FOA)是由潘文超[1]在2012年提出的，是基于仿生果蝇群体觅食行为的寻优算法；文献[2]对果蝇算法和其他算法进行了对比，结果表明果蝇算法简单、参数少、运行效率高，并且在进化次数低时[2]，果蝇算法比混合跳蛙算法[3]、和声算法、人工蜂群算法的收敛精度和收敛速度都高，适合于实际应用或与其他算法结合进行分阶段优化。但是，FOA和其他全局优化算法一样，标准果蝇优化算法也容易陷入局部最优，特别对于高维多极值复杂优化问题，在搜索计算后期收敛速度变慢，收敛精度降低。FOA算法目前的优化途径大致分为两种：对算法自身的改进；将FOA算法与其他算法结合，产生新算法。其中文献[4-5]将果蝇算法的固定步长改进为自适应步长；文献[6]将果蝇群分为搜索果蝇和跟随果蝇，分别进行全局和局部搜索；文献[7]将FOA算法与差分算法相结合，提高果蝇种群多样性；文献[8-9]也都是通过与其他算法相结合，弥补果蝇算法缺陷。智能群算法的改进应该遵循“内部完善-外部提升”[10]，但是目前少有学者对果蝇算法自身的搜索特性进行改进。

针对上述问题，提出了一种基于扇区搜索机制的果蝇优化算法，并将该方法应用于K-means算法优化。本文首先介绍了果蝇算法工作原理和扇区搜索机制搜索原理，然后将改进的果蝇算法用于K-means聚类算法的优化，最后通过对比实验验证改进的FS-K算法具有更好的聚类效果。

1 果蝇算法

果蝇优化算法是一种仿生果蝇群觅食行为的算法，模拟了果蝇群的两种觅食搜索方式：嗅觉搜索(果蝇群捕捉空气中的气味逼近气味源)和视觉搜索(果蝇个体在靠近气味源的同时，使用视觉发现食物与种群位置，并靠近)[1]。

果蝇算法模拟果蝇觅食行为可以总结为以下7步:

Step1 初始化参数：群体规模S，最大迭代数M_G，随机初始化群体坐标X_axis，Y_axis。

Step2 在群体坐标周围，随机生成S个果蝇个体，L为搜索半径：

Xi=X_axis+L*(2*rand()-1)

Yi=Y_axis+L*(2*rand()-1)

Step3 由于无法得知食物位置，先计算果蝇个体与原点的距离Di，并将其倒数作为果蝇个体的味道浓度判定值Si:

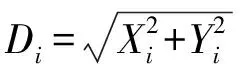
Step4 将果蝇个体的味道浓度判定值Si带入味道判定函数(即目标函数)，计算果蝇个体味道浓度值Smli:

Smli=Function(Si)

Step5 找出该果蝇群体中味道浓度最佳的果蝇(最小值或最大值):

[b_Smlb_index]=min (Smli)

Step6 将果蝇的最佳味道浓度值b_Sml保存下来，并且记录最优个体的坐标值作为群体坐标：

X_axis=X(b_index)Y_axis=Y(b_index)

Step7 通过迭代运算，进行寻优，重复执行上面的 step 2—step 5，并判断最佳味道浓度是否优于前一迭代最佳味道浓度，并且判断当前迭代次数是否小于最大迭代次数M_G，若是，则执行Step 6。

2 扇形搜索果蝇算法

2.1 扇形搜索原理

FOA算法在进行随机搜索时，其果蝇群产生机制是围绕群体坐标进行随机搜索:

Stacking算法既能集成各基分类器的训练结果，也能组合各种可能决定分类的相关信息，因此普遍认为其性能优于贝叶斯投票方法[41]。

Xi=X_axis+R,Yi=Y_axis+R

其中R为[-L,L]的随机数。这种搜索机制在二维空间上表现为中点为种群坐标，边长为2L的正方形，果蝇的搜索范围如图1所示。这样的搜索机制使果蝇群在搜索时总是趋向于沿着单一方向移动，限制了果蝇群搜索方向的多样性。

图1 FOA果蝇群搜索范围

针对果蝇群搜索范围的不平衡性，本文提出一种扇形搜索机制，该机制在果蝇随机搜索时，以果蝇群坐标为中心，把搜索区域划分为n个扇区，每个扇区均生成果蝇个体。具体实现方法如下:

① 划分扇区，其中t为扇区角度;

② 在群坐标周围产生果蝇群，其中L为果蝇群搜索半径，rand()为[0,1]的随机值;

Xi=Xaxis+L*sin(t)*rand()Yi=Yaxis+L*cos(t)*rand()

对FOA和FS-FOA算法进行单独5次的运行，对比了果蝇群的迭代路径，如图2。由图2可以看出：FS-FOA果蝇群在搜索食物时，有4次向上方飞行，有1次向右方飞行，而FOA果蝇群的迭代方向较为单一，总是趋向于沿着Y=X的方向飞行。说明基于扇形搜索机制的果蝇群在寻找食物源时，在种群前进方向上的选择性增加了，相较于FOA算法，FS-FOA算法的果蝇群总是朝着味道浓度最大的方向前进，而FOA算法在迭代中受到搜索范围的影响，方向单一，无法朝着味道值最优的方向前进，使得FOA算法的收敛较慢，在高维度函数优化问题中，还会陷入局部最优。

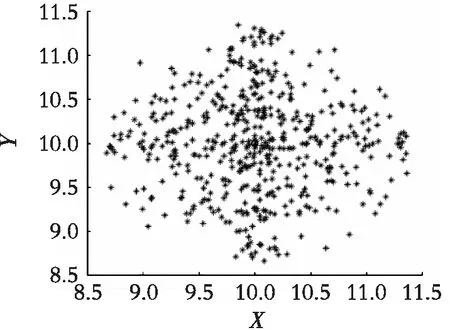
图2 FS-FOA果蝇群搜索范围

2.2 果蝇趋利特性

在自然界，果蝇在觅食过程中，其并不是随机在一个范围搜索，而是多数果蝇朝着食物源的方向飞行，少数果蝇向着其他方向搜索。受此启发，FS-FOA对果蝇个体赋予了不同的性质：趋利性和盲从性。盲从果蝇在果蝇群坐标周围随机搜索，趋利果蝇则更有方向性，总是朝着食物源一侧快速飞行，在食物源单一的情况下，趋利果蝇能够帮助算法减少无效迭代并快速收敛，在相同的迭代次数下，FS-FOA算法总能达到更高的收敛精度。

趋利果蝇的个数由趋利因子R决定，趋利果蝇个数q=S*R，其中R∈[0，1]，R取值越大，果蝇的趋利性越强，但是R的取值不应超过0.5，超过0.5会导致果蝇群忽略对味道源方向的判别。趋利果蝇的方向由趋利果蝇的个数决定，其生成方法如下：

(1)

趋利果蝇的搜索步长采用自适应步长，其步长值计算如式(2)所示：

Lq=L*ln(gen+3)

(2)

其中，L为盲目果蝇的搜索步长，gen为迭代时所属方向的累计代数，gen的取值范围为gen∈[0,M_G]。趋利果蝇的自适应步长会使其拥有较高的加速度，能够较快确定食物源确切方向并向目标源飞行，同时在确定了食物源方位后也不会因为有太大的步长而忽略食物源。趋利果蝇的生成策略如式(3)所示:

Xq=X_axis+Lq*sin(θ)Yq=Y_axis+Lq*cos(θ)

(3)

3 FS-FOA算法优化K-means聚类算法

聚类算法是数据分析经典算法，属于无监督学习算法，K聚类算法的目的是将数据分为指定类，尽可能使类内样本相似度大，类间相似度小。由于算法较简单且有极强的收敛性，K-means聚类算法在处理大数据的应用背景下有广泛的应用。但是K-means聚类对初始聚类中心的选取依赖性很大，极易陷入局部解。目前比较流行的优化方法是使用群优化算法对K-means算法进行优化，减少聚类算法对初始聚类中心的敏感度[11]。

针对K-means对初始聚类中心依赖性大的缺点，本文结合FS-FOA较强的全局搜索能力与K-means算法的快速收敛性，将FS-FOA与K-means相结合产生一种新型聚类算法FS-K。FS-K相较于FOA能够较快收敛，并通过迭代寻找全局最优值，避免陷入局部最优。

算法流程如下：

Step1 对FS-K算法进行初始化:种群个数Sizepop;最大迭代次数maxgen;聚类中心数Knum。

Step2 初始化果蝇群，从样本中随机抽取Knum个数据作为一个果蝇个体，每个果蝇个体表示一种聚类中心。

Step3 将果蝇个体作为K-means的初始聚类中心，收敛得到的聚类中心作为果蝇个体的初始位置。

Step4 数据点距离所属聚类中心的欧式距离之和作为味道浓度判定函数，计算果蝇个体适应度，选择最优果蝇个体作为种群初始坐标。

Step5 在种群坐标周围随机生成果蝇群，计算果蝇个体的味道浓度，记录最优个体的味道浓度以及位置信息。

Step6 判断果蝇最优个体是否优于当前最优，如果是，将最优个体作为下一代的果蝇群坐标。

Step7 进入迭代寻优并重复执行Step5—Step6，直到达到最大迭代次数Maxgen。

4 试验与分析

4.1 优化函数测试

为了验证FS-FOA的聚类效果，采用了5种常用的测试函数进行仿真测试。为了更好对比算法的优化性能，将测试分为固定迭代次数和固定精度两种。其中固定迭代次数试验中，FOA与FS-FOA算法的最大迭代次数均取M_G=100，种群大小S=30，为保持FOA与FS-FOA的种群大小一样，把FS-FOA中盲从果蝇数量设置为20，趋利果蝇数量设置为10。固定精度试验是为了测试算法在目标精度下的迭代次数和运行时间，通过对比不同精度的函数优化来对比算法的收敛性。为了保证试验的可靠性，在初始化时，将FOA的初始化果蝇坐标X_axis，Y_axis也作为FS-FOA的初始化坐标，并将FOA与FS-FOA算法各独立运行30次，取其优化结果的平均值、最优值和方差作对比。固定迭代次数的试验结果如表2所示，在目标精度下寻优对比结果如表3所示。

表1 测试函数

表2 固定代数寻优结果对比

由表2可以看出：FS-FOA算法在处理单峰函数F1(x)，F5(x)时，寻优精度会比FOA算法高出一个数量级，在处理多峰函数F2(X)，f4(x)时，寻优精度比FOA高出两个数量级，说明FS-FOA在处理多峰函数时性能提升更明显;此外，FS-FOA的方差在处理F1，F2，F3，F5时，要比FOA的方差高出4个数量级，在处理二维函数F4时，方差与FOA算法有相同数量级，说明FS-FOA算法在处理高维函数时，其寻优能力更强，稳定性更高。

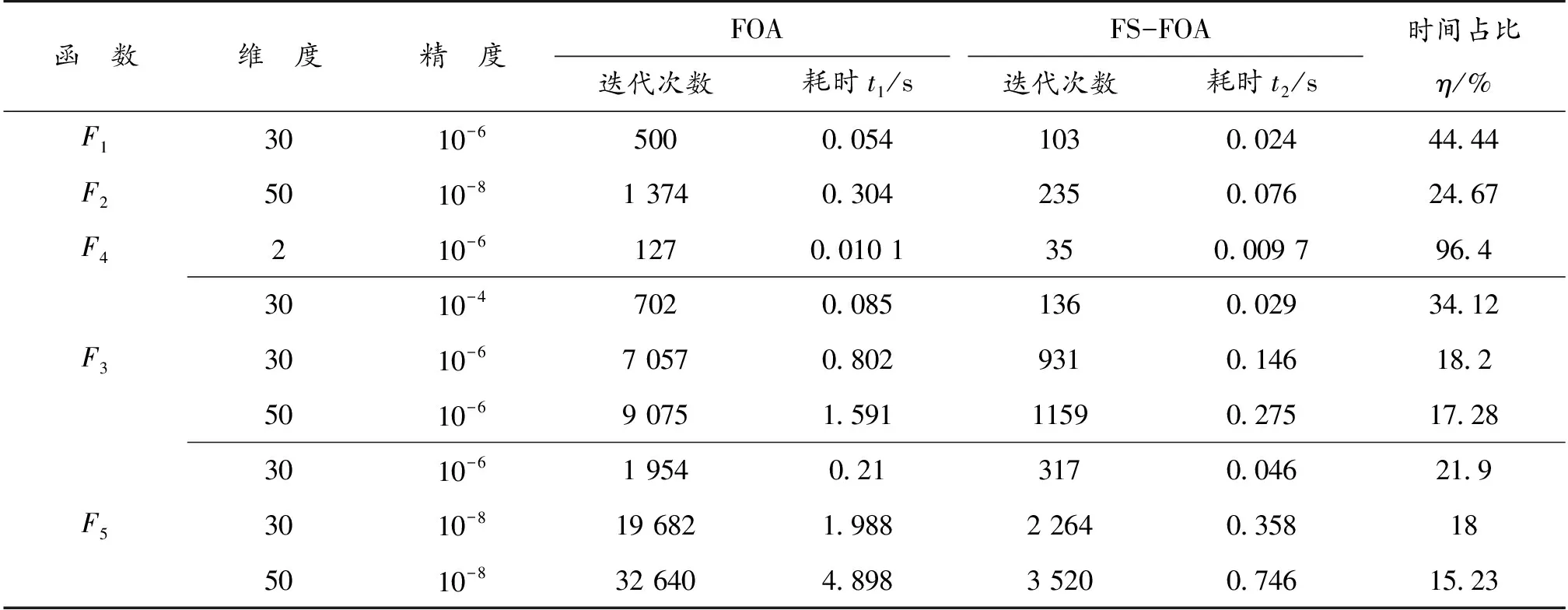
表3 目标精度寻优时间对比

对表3进行分析可知: FS-FOA算法在目标精度下的寻优时间和代数更少，对于30维F1，F2函数；FS-FOA所用时间占比为44.44%和24.67%，其中时间占比η=t2/t1，FS-FOA在处理F4函数时，时间占比为96.4%，与FOA耗时差不多，这是由于处理低维函数时，所用迭代次数太少，在时间上差距不大。但是从F3和F5函数可以看出，FS-FOA在处理目标精度更高的寻优时，其优化性能更明显，对F3函数30维在10-4和10-6精度下寻优对比，发现时间占比缩小了15.9%，对比10-6精度下30维和50维，则缩小了0.9%，说明FS-FOA是精度更高的寻优算法，其寻优性更好。

4.2 聚类试验及对比

实验采用UCI标准数据集库中的Iris，Wine，Glass，和CMC 4个数据集进行性能测试。仿真实验参数设置：初始种群个数S为50，最大迭代数为100，每组数据独立运行30次，取数据样本距离所属聚类中心的欧式距离和作为算法的适应度函数，对K-means，FOA，SOM，FCM以及FS-K的聚类结果进行对比。表4为试验得到的30次独立试验的最小值、最大值和均值。

表4 聚类结果对比

表4可以看出：FS-K的聚类结果在稳定性上要比K-means和FOA高，并且总能跳出局部解，逼近最优值，和另外两个经典算法SOM，FCM进行对比，具有更好的聚类效果。从图3可以看出，在收敛性上，K-means的收敛速度最快，能够在10代左右收敛；FS-K收敛较慢，在迭代50次左右趋于稳定；FOA收敛速度要快于FS-K，但是容易陷入局部解，其跳出局部解的能力没有FS-K强。

图3 Iris数据集聚类曲线对比

5 结 论

提出了一种扇形搜索的果蝇优化方法，弥补了果蝇算法在搜索中受限于搜索范围的缺点，增加了果蝇算法跳出局部解的能力和收敛速度。在维度高的函数优化问题中，FS-FOA算法的效果更加显著。随后，将FS-FOA算法与K-means算法相结合，提出一种优化聚类方法FS-K，并使用UCI数据集进行测试，验证了算法的可行性。但是，采用改进后的FS-K算法的聚类收敛的速度较慢，如何提高FS-K聚类的收敛速度是未来进一步的研究方向。