一种新的电能质量扰动识别方法*

武昭旭， 杨 岸， 祝龙记

(安徽理工大学 电气与信息工程学院,安徽 淮南 232000)

0 引 言

随着电力系统的发展、电源接入形式多样化、负荷种类的增加，电网中的电能质量问题越来越突出。因此，准确、快速地对电能质量扰动信号识别，是保障电网稳定、安全、高效运行的前提。

目前，国内外学者针对电能质量扰动信号识别分类进行了深入研究，方法主要有：傅里叶变换[1]、小波变换[2]、S变换[3]、希尔伯特黄变换[4]、相空间重构[5]等。文献[6]利用小波变换将原始扰动信号分解到各个频带，分别计算各个频带的能量值和小波系数熵，将二者及基波频带扰动过程的均方根作为特征值输入到改进神经树进行分类，分类准确率较高，但所选扰动均为单一扰动信号。文献[7]利用稀疏自动编码器对原始扰动信号进行无监督特征学习，自动提取数据特征的稀疏特征表达，随后使用Softmax分类器进行训练，得到各种扰动信号的分类准确率，解决了传统神经网络中权值初始随机性的缺点，但编码过程复杂。

通过对现有电能质量扰动信号识别方法的研究可知，各种识别方法通常可分为两个步骤：特征提取和特征分类。特征提取是使用不同的时域、频域信号分析方法提取能反映不同扰动信号的判别信息，特征分类是通过训练不同的分类器实现对扰动信号特征的识别。本文所提方法可以充分减少扰动识别过程中所需处理的数据量、简化识别过程、提高识别速度和识别准确率。

针对电能质量扰动信号数据多、识别率低、识别速度慢等问题，将基于一维卷积神经网络的压缩感知算法应用于电能质量扰动信号的分类。首先阐述了如何使用压缩感知理论对电能质量扰动信号求解稀疏向量，然后提出了基于一维卷积神经网络的分类模型，实现电能质量扰动信号的分类。

1 基于压缩感知理论的电能质量扰动信号压缩与重构

1.1 压缩感知理论

2006年， Donoho等[8]提出了压缩感知理论(Compressed Sensing,CS)。该理论指出如果信号是稀疏的，则可以在远低于Nyquist采样频率条件下重构。即：如果一维信号XN×1在稀疏域Ψ是K-稀疏的(K≪N)，则构造一个与变换域Ψ不相关的观测矩阵ΦM×N(M≪N)，对原始信号进行观测：

Y=ΦX=ΦΨS=ΘS

(1)

其中，Θ=ΦΨ，称之为感知矩阵，Φ为测量矩阵，Ψ为稀疏矩阵，SN×1为稀疏域中的稀疏向量。对求解0-范数，则可以得到重构信号

(2)

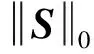
1.2 电能质量扰动信号压缩与重构

电能质量扰动信号并非直接符合稀疏性，但是可以通过某种变换得到稀疏性的效果。即找到一种稀疏变换基Ψ=[ψ1,ψ2,…,ψN]，将扰动信号X表示为

(3)

其中，S=[S1,S2,…,SN]是电能质量扰动信号X在变换域Ψ的表示。采用离散傅里叶变换(DFT)作为稀疏变换基[9]。

测量矩阵是一个M×N的矩阵，设计测量矩阵的目的是获取原始信号X的M个测量值，使观测信号Y中的M个值可以有效地保留原始信号X中的信息。测量矩阵的优劣直接关系到原始信号的恢复效果，选用高斯随机矩阵作为扰动信号的测量矩阵。

重构算法就是把采集到的观测值YM×1利用测量矩阵Φ和稀疏变换基Ψ来恢复原始信号，使用正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)进行压缩重构[10]。图1为电能质量扰动信号压缩感知流程图。

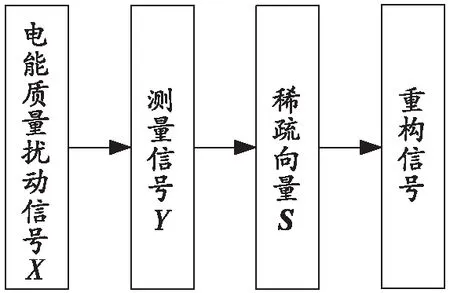
图1 电能质量扰动信号压缩感知流程

1.3 算例分析

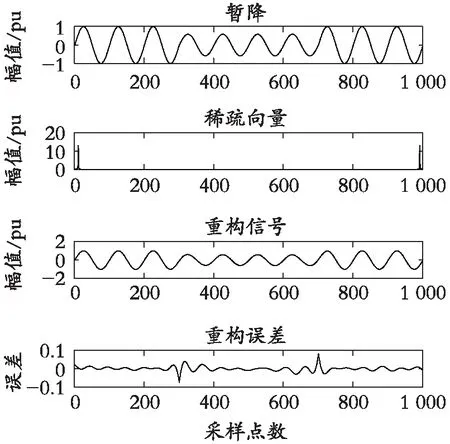
根据IEEE建立8种单一电能质量扰动信号和6种复合电能质量扰动信号，分别为正常信号(C1)、暂升(C2)、暂降(C3)、中断(C4)、谐波(C5)、脉冲(C6)、振荡(C7)、波动(C8)、暂升+脉冲(C9)、暂降+脉冲(C10)、谐波+波动(C11)、波动+脉冲(C12)、谐波+暂升+脉冲(C13)和谐波+波动+振荡(C14)，以 3种电能质量扰动信号(暂升、暂降、谐波+波动)为例，分别进行仿真，其中电能质量扰动信号长度N=1 000，测量数M=256，稀疏度K=16。图2为3种扰动信号的压缩重构图，对比3种稀疏向量波形可知，使用稀疏向量不仅极大地减少了分类过程中处理的数据量，而且不同扰动信号的稀疏向量特征分明，便于后续分类；重构信号的重构误差相对较小，可以精确地恢复原始信号。

(a) 暂升

(b) 暂降

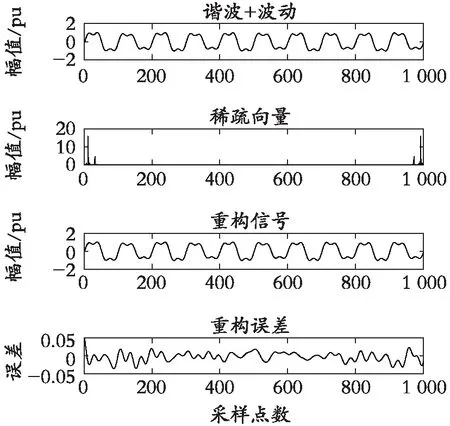
(c) 谐波+波动

2 基于一维卷积神经网络的电能质量扰动信号分类

2.1 一维卷积神经网络

深度学习[11-14](Deep Learning,DL)作为一种机器学习方法，在图像识别、语音处理等领域都取得了不错的成果。其中常用于图像识别领域的卷积神经网络，被发现对时间序列数据同样有效，因此使用一维卷积神经网络[15-16](One-Dimensional Convolutional Neural Network,1D-CNN)处理一维电能质量扰动信号数据。1D-CNN可以自动学习、提取电能质量扰动信号的时序特征，实现对扰动信号的分类。

1D-CNN与二维卷积神经网络类似，由卷积层、池化层、Dropout层和全连接层等组成。卷积层通过卷积操作实现对输入层的特征提取。池化层对卷积层生成的特征图进行压缩，简化网络计算复杂度和提取主要特征，实现对特征图的降维。卷积层与池化层的堆叠组成深层的神经网络结构，实现对输入数据特征的组合和局部不变。

卷积层做卷积运算时，需要将卷积核放在输入数据上，二者的中心位置需要重合。依次计算卷积核与其对应位置数据值的积并求和，最后计算得到的是特征图中该位置的值。由式(4)可知，如果X1,m表示输入数据的第1行第m列的值；W1,n表示卷积核的第1行第n列的权重值；Wb表示卷积核的偏置值；a1,m表示特征图的第1行第m列的值；用f表示网络使用的Relu激活函数，则一维卷积如图3 所示。

(4)

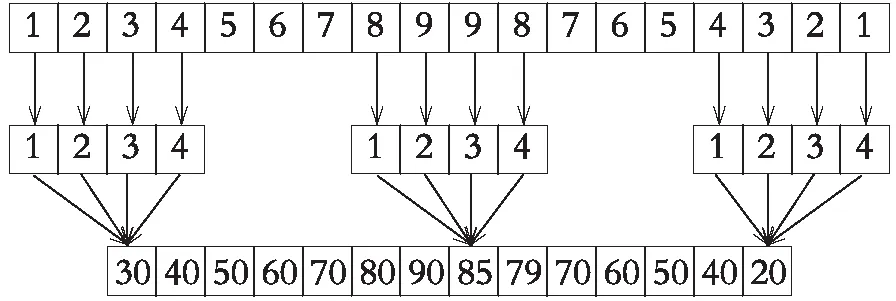
图3 一维卷积

池化(Pooling)也称为下采样。池化可以理解为在不影响对数据的特征收集条件下对数据降维，即减小特征图的大小，池化可分为均值池化(Mean Pooling)、最大池化(Max Pooling)等。一维池化如图4所示，池化核大小和池化步长均为3，采用最大池化。

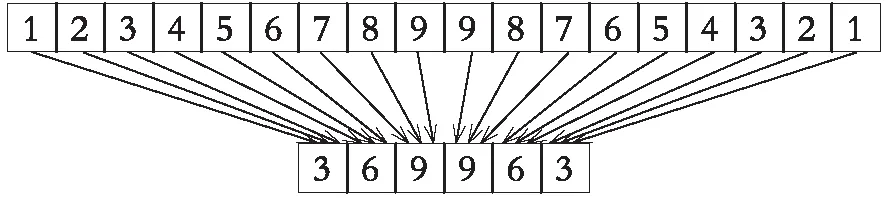
图4 一维池化

全连接层将卷积层、池化层提取到的局部特征通过权值矩阵形成完整的图形，在整个卷积神经网络中起到“分类器”的作用，层中的每个神经元与前一层所有神经元进行连接。全连接层的输出值传递到输出层，输出层激活函数通常是Softmax函数，输出各分类类别的概率。

2.2 一维卷积神经网络模型结构

通过 Tensorflow中的Keras 框架实现卷积神经网络，该网络有4个卷积层、2个池化层和1个全连接层。输入1D-CNN的电能质量扰动信号大小为 1×1 000，卷积层采用 1×10卷积核，步长为1，选择 ReLU 函数为激活函数；池化层采用Max-Pooling，池化窗口大小为 1×3，步长为 1；全连接层的输出结果是一个1×14的向量，即输入样本属于对应标签的可能性大小，最后输出扰动信号的14分类识别率。分别设置参数：Epoch为50，损失函数为Categorical_crossentropy，Optimizer为Adam，Dropout为0.5。

3 仿真分析

采用 MATLAB 生成14种电能质量扰动信号，正常信号和每类扰动信号各生成 1 000个随机样本，共14 000个样本。每类扰动分别叠加信噪比(SNR)为 30 dB的噪声信号。每类扰动选取 800个样本作为训练集，200个样本作为测试集。再通过压缩感知理论计算每个扰动信号的稀疏向量，形成基于稀疏向量的样本集。将原始信号和对应的稀疏向量数据作为一维卷积神经网络的输入，运行并训练搭建好的网络分类模型。

为了评估网络的分类性能，绘制训练损失曲线和识别率曲线。训练损失曲线如图5 所示，识别率曲线如图 6所示。从图5可以看出，原始数据和稀疏向量的训练损失均在不断下降，其中原始数据对应的损失曲线快速下降并保持在一个较低的数值；稀疏向量对应的损失曲线下降缓慢，但最终仍保持在一个较低的数值，说明预测标签与实际标签的差距很小，网络的分类性能很好。由图6可知，其中原始数据对应的识别率经过约10代的训练，快速上升并保持在一个较高的数值，此后网络参数不断进行微调，识别率趋于稳定，大约为99%;稀疏向量对应的识别率则由一个较低的初始值缓慢上升，经过50代的训练后，保持在一个较高的数值。

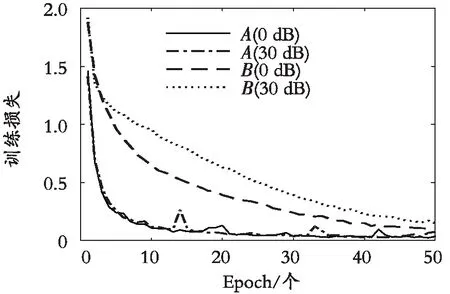
图5 训练损失曲线

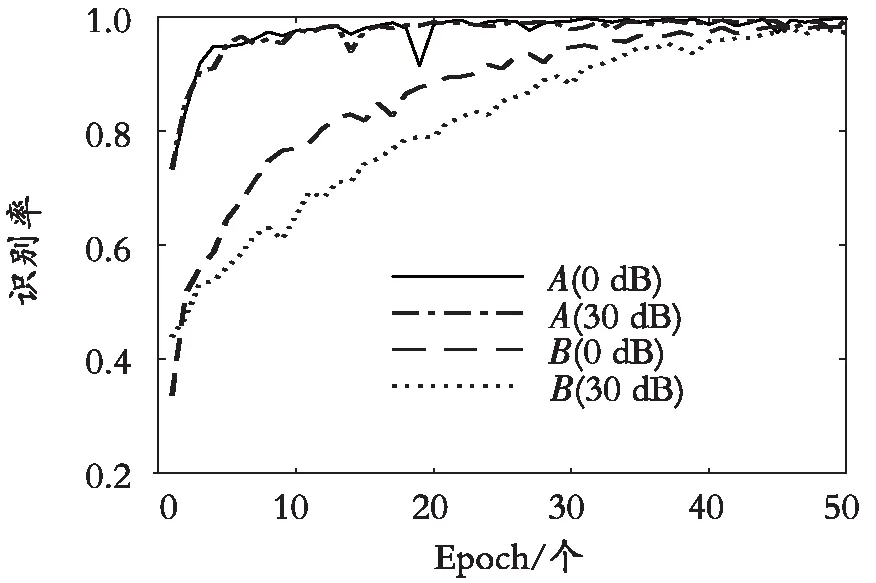
图6 识别率曲线

不同的噪声强度下，各类电能质量扰动信号的分类准确率结果如表 1 所示。其中，A为原始数据，B为稀疏向量。

表1 不同信噪比下扰动信号的分类准确率

由表1可以看出：本方法在不同的噪声强度下对扰动分类的总体准确率均较高，多种扰动在不同噪声情况下均可达到较高的识别率，说明该方法具有较好的抗噪性能。但是稀疏向量较原始数据输入的识别率有所下降，这是因为重构过程中产生了重构误差，导致了扰动信号中信息的丢失。

4 结束语

使用一维卷积神经网络对扰动信号经压缩感知生成的稀疏向量进行学习，可以有效地提取扰动的特征。通过处理长度仅为16的稀疏向量而不是长度为1 000的原始信号，减少了分类过程中需要处理的数据量，提高了识别速度。在不同的噪声情况下，将原始数据和稀疏向量分别作为网络的输入，由实验结果可知，该方法能获得较高的识别率，具有良好的抗噪能力。