基于几何画板技术的问题提出教学策略探究

王文义 朱惠英 何男

摘 要：本节课运用问题提出教学模式，循序渐进，层层设问，引导学生探究归纳出指数函数定义。运用几何画板动态效果，生动形象地绘制出指数函数的图像，让学生对知识函数的定义和性质体会更深。同时在学习指数函数的过程中渗透辩证唯物主义的思想，把学生培养成为具有哲学思想的人。

关键词：指数函数;底数;指数;辩证唯物主义

一、 创设情境，引入实例

教师提出问题：同学们玩过折纸吗？你相信一张纸能带你上月球吗？带着这个问题，我们来进入今天的学习内容。

接下来教师播放1分10秒的小视频《指数爆炸》，并请学生在观看后回答问题：折纸的过程中，纸张的哪两个属性会发生变化？

学生回答：纸的厚度和面积。

教师：假设一张纸的厚度为1个单位，面积为1个单位。理想状态下，如果不考虑纸的延展性，这张纸可以折叠无数次。当这张纸折叠1次，2次，3次，乃至x次时，你能推算出纸的厚度和纸的面积分别是多少吗？请同学们通过小组合作，完成下表。（小组合作探究后请两个小组代表发言）

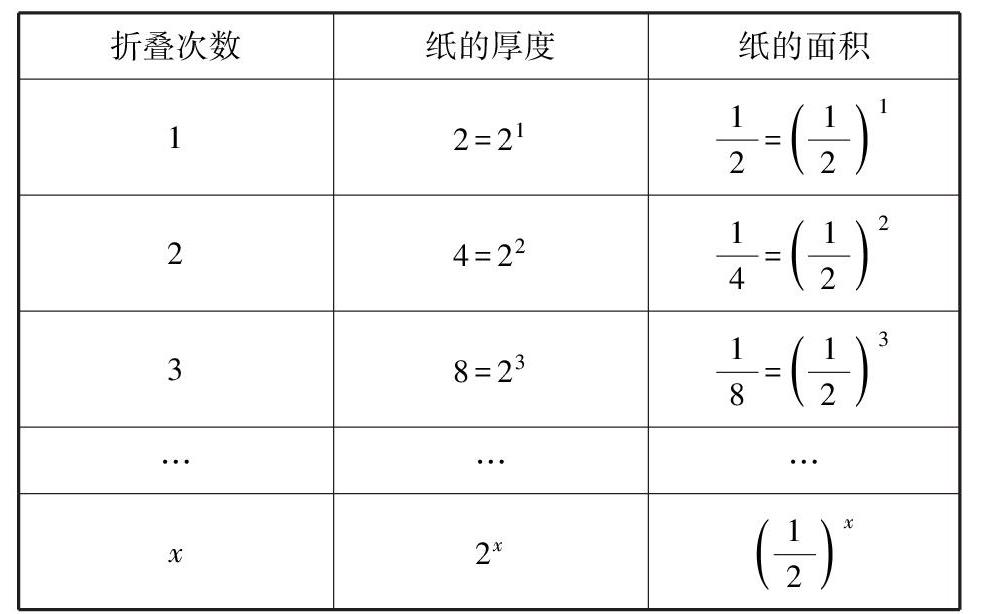
学生填写表格：

折叠次数纸的厚度纸的面积

12=2112=121

24=2214=122

38=2318=123

………

x2x12x

教师：由表格，我们能得到哪两个函数解析式呢？

学生：一是纸折叠后的厚度与折叠次数的函数y=2x，二是纸折叠后的面积与折叠次数的函数y=12x。

设计意图：学生通过反复折叠纸的操作过程，分别抽象出指数函数y=2x，y=12x，既满足了指数函数按底数划分的两类函数，又满足了教材上所举的函数例子，达到了灵活处理教材的目的。纸在反复折叠的过程中，随着折叠次数的增加，厚度呈指数型增长，而面积却呈指数型减少，学生可初步感受由底数不同带来的指数函数性质的不同，充分经历从数学情境中抽象出指數函数特例的过程，为后面引出指数函数的概念做铺垫。

二、 讨论底数，归纳结论

教师提出问题：函数y=2x，y=12x，与我们之前所学的函数有何不同？

（提示：未知数的位置在哪？）

教师：像这种指数位置为x，底数位置为常数2或者12的函数，我们称之为指数函数。也就是说，形如y=ax的函数叫作指数函数（此时板书定义的一部分）。大家还能举几个例子吗？

教师提出问题：底数a为负数可不可以？如y=-3x。

学生回答：指数函数底数为负数会导致某些值没有意义，比如x=12。

教师：为了让x取遍所有的实数，规定指数函数的底数为正数，即底数a>0。

教师提出问题：除了底数a>0，同时底数还要满足什么条件？

学生回答：底数不等于1。当底数a=1，那么1x=1，没有研究的意义。

教师继续板书补充指数函数的定义：形如y=ax（a>0，且a≠1）的函数叫作指数函数。

设计意图：指数函数是高中阶段学习的第一个函数，不同于初中学的函数。引导学生观察指数函数底数位置和指数位置，未知数x在指数位置，再辨析底数a的取值范围，这一过程经历了特殊到一般，具体到抽象的过程，有利于培养学生的数学抽象素养。

教师介绍指数函数的历史出处：

1748年时，世界著名数学家欧拉，在著作《无穷分析引论》（Introduction to Analysis of the Infinite）中对指数函数进行了明确和详细的介绍。

设计意图：让学生了解指数函数的出处和产生时间，有利于让学生了解知识产生的背后，数学家起着重要的作用。

【例1】 下列函数是否是指数函数。

（1）y=2·3x

（2）y=-3x（系数错误）

（3）y=（-4）x（底数错误）

（4）y=x3（指数错误）

（5）y=3-x

（6）y=πx（正确）

当学生回答正确时，追问学生回答为什么不是指数函数，分别表扬学生突破了系数、指数、底数错误关卡。

接着，教师帮助学生总结判断一个函数为指数函数y=ax（a>0，且a≠1）需满足的条件：（1）系数为1;（2）底数a>0，且a≠1;（3）指数位置仅有自变量x。

设计意图：例题1有利于加深学生对指数函数概念的理解与掌握，同时通过关卡这一游戏氛围，激发学生的学习兴趣。

三、 对象阶段：利用技术，探索性质

教师：研究函数一般从函数的图像分析函数的性质，你还记得用什么方法画函数的图像吗？

学生回答：描点法。

教师提问：你能用描点法画出指数函数y=2x的函数图像吗？

学生画好图像后，教师也用几何画板展示出图像（这里可以适当表扬学生）

设计意图：学生动手操作，初步感知指数函数的图像，积累数学活动经验。

教师提出问题：同学们现在可以根据这个特殊的函数图像发现指数函数的性质，如奇偶性、周期性、对称性、单调性吗？

学生摇摇头说：发现它在定义域上单调递减的。

教师：除了这一点，别的发现不了对不对？回到我们指数函数的定义，同学们有没有注意到指数函数的底数是会变化的呢？

学生：对，会变化。

教师：那我们可不可以利用底数的变化来找到指数函数的性质呢？其实，马克思的辩证唯物主义思想给了我们答案。我们一起来看一下。马克思曾说，事物的运动发展是变与不变的统一。我们要认识与把握不变中有变，变中有不变。这个“变中有不变”即如：虽然我国成为世界第二大经济体，经济实力和综合国力显著增强，但我国仍处于并将长期处于社会主义初级阶段的基本国情没有变。所以我们仍需不断努力，不断奋斗。那么，同学们说，我们应如何利用“变中有不变”这一思想来发现指数函数蕴含的规律呢？