基于地质模型的定向组合激发-接收技术

李亚林，徐峰，彭更新，刘福烈，郭念民，徐凯驰

1 中国石油塔里木油田公司，新疆库尔勒 841000 2 西南石油大学，成都 610500

0 引言

震源激发的能量只有一小部分投射向目的层并最终返回地表，带回了地下反射信息，其他大部分由于地层临界角度、接收排列长度限制只能在近地表附近传播，这部分能量传播过程中与近地表的非均匀介质作用形成了大量的噪声，降低了地震资料信噪比(徐峰等，2011).提升资料信噪比有两种思路：一种是绝对地提升采集数据中的反射能量，这就要增加震源初始能量，根据Sharpe(1942)的理论，爆炸压力产生的弹性波振幅正比于爆炸空腔的面积和爆炸压力，扩大爆腔和爆压就需要更大的炸药药量，而大量的生产实践表明，激发能量不会随着炸药用量线性增加，当达到一定用量后，能量基本不再变化——存在饱和激发现象(凌云，2001；杨贵祥，2005)；另一种思路是相对提升能量，将激发后的能量约束聚焦在向目的层投射的角度方向上，同步压制噪声能量源，进而提升信噪比.本文探讨后一种方法.

波具有方向性，对波的方向性利用较早的是军事上的相控阵雷达(Dolph，1946)，出于对空搜索目标的需要，成百上千个发射/接收单元被组合在一个天线上，通过聚焦波束增强探测距离和精度.地震波的方向性验证是20世纪70年代美国石油公司在Oklahoma的Tulsa地区做过的地震波束形成实验，该实验证明了地震波的定向方向可以通过延时时间间隔调节(Arnold，1977).2002年吉林大学林君教授课题组自主研发的相控震源系统也是基于地震波可以定向的理论(Chen and Lin.，2003).随后，姜弢等(姜弢等,2004; 姜弢，2006)对定向地震波信号的信噪比和分辨率进行了定量分析，证明了基于相控震源的定向地震波方法在理论和实践上的可行性和优越性.

目前，无论是产生电磁波的相控阵雷达还是产生地震波的相控震源，都是研究定向波的传播，对于事先未定向的单点激发的波场数据，是否存在后期进行室内定向组合的可能，鲜有讨论.排除掉耦合性差异，波场符合线性叠加原理——即，A、B两个炮点单独激发后再叠加的波场应该与它们同时激发的波场保持一致，两个检波点单独接收的波场叠加结果应该与它们组合接收的波场保持一致.这为室内定向组合处理提供了理论依据.

进行室内定向组合首先需要知道待组合的方向，这个方向可以从波场自身的方向分解中求取.Yoon(2004，2011)在进行逆时偏移成像研究的时候，引入坡印廷矢量来计算传播中波场的方向和倾角信息，为解决计算稳定性问题随后又进行了子波多周期叠加、时窗平滑等技术改进，他的一系列研究为室内定向组合技术提供了求解思路.秦龙等(2019)用Yoon的方法，计算了波场传播到地表的方向，推进了室内组合的实用化.

进行室内定向组合还需要确定具体的组合参数.有关组合参数设计的研究较多，Johnson(1939)从天线理论出发，推导了组合响应函数的表达式，成为组合参数设计的依据，Holzman(1963)、Rietsch E(1979)提出的切比雪夫多项式逼近方法通过调整加权系数来逼近需要的组合响应；Vermeer(2002)研究了组合形态的影响，得出四点菱形震源组合和28点圆形检波器组合在360°的范围内可均匀的获得40 dB噪声衰减的结论；Johnson(1968)研究通过时差控制来改变组合响应的方法，由检波器位置确定组合延时量；King等(1973)采用参考道与各独立地震道做互相关的方法确定延时量；秦龙等(2019)在其炮点组合的研究中也使用了时间延迟的方法来实现方向聚焦；徐峰等(2020)在检波器组合的研究中给出了组合个数、间距、时差、加权多元参数联合运用的设计方法.

本文总结前人研究成果，利用了地震波的方向性，将方向性求取技术和多元组合参数设计技术结合起来，对已采集的地震数据进行室内组合处理，达到相对提升信噪比，改善目的层成像的目的.

1 方法原理

1.1 能量定向传播机理

在各向同性介质中传播的地震波不会发生方向选择——不同方向间的能量强弱关系一致.但当地震波传播到地层界面，由于透射/反射，能量会在界面两侧重新分配，这种分配与入射角度、界面两侧的弹性参数有关.广为接受的Zeoppritz方程描述了界面处能量的分配关系，式(1)给出了它较为常用的Shuey(1985)近似式：

RP(θ)=R0+Gsin2θ+F(tan2θ-sin2θ),

(1)

其中RP为纵波入射下的界面反射系数，θ为纵波入射角，公式分三部分，R0代表法向入射时纵波反射系数，中间的Gsin2θ代表中等入射角项，最后一部分F代表大角度入射项.图1给出了VP1=2500 m·s-1,VP2=2700 m·s-1,VS1=1800 m·s-1,VS2=1900 m·s-1,ρ1=2.0 g·cm-3,ρ2=2.5 g·cm-3参数下的界面反射系数随入射角度变化曲线，可见随入射角增大，反射系数先减小后增大.

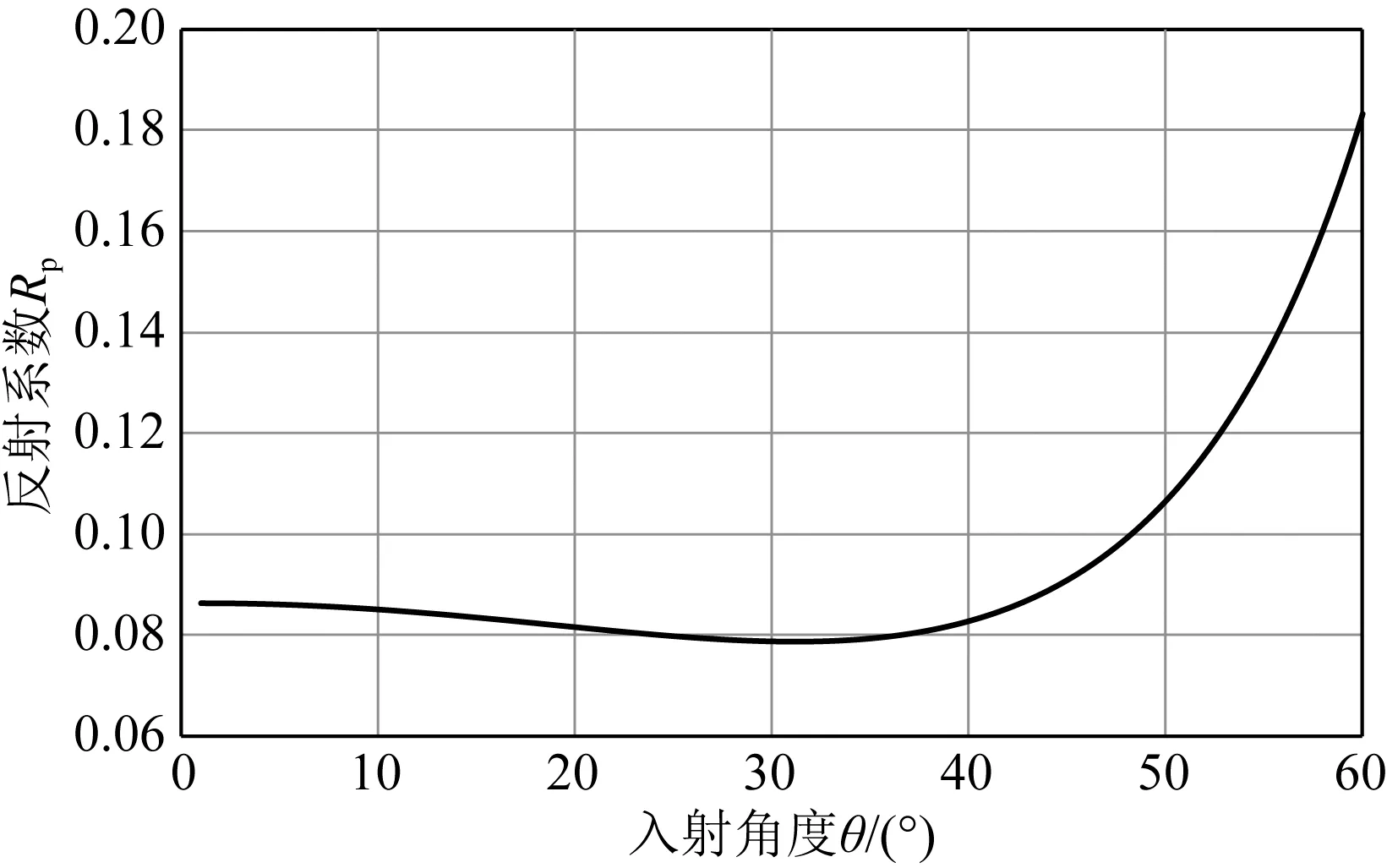
图1 界面反射系数随纵波入射角度变化曲线

界面的存在使传播中的地震波能量在不同方向上发生了改变，这种改变会随地层的弹性参数不同而不同，当地层自身倾角较大时，方向性变化会更加明显.地震波在地层界面上发生能量的重分配，是波场具有方向性的根本原因.

下面以Marmousi模型为例来展示地震波传播的方向性.图2为Marmousi模型的叠前时间偏移剖面，在地下R点(9250 m,2370 m)设置震源，激发地震波，得到图3所示的波场照明图，可以看到因复杂的地层接触关系，上传地震波场在不同方向上能量差异较大，较强的能量分布在一些弯曲的“亮线”中以特定角度出射地表.保持模型结构不变，激发点R位置不变，则地下能量传播的路径结构不会改变，出射到地表的地震波能量大小及角度也会被唯一确定.强能量意味着能量投递的高效率，在地表强能量位置，强迫震源逆向出射角度下传更多能量，强迫检波器更多地接收出射角度上传的能量，即可实现增强弱成像区照明的目的.

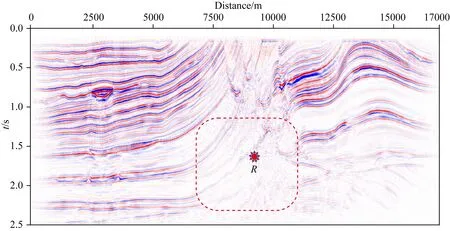
图2 Marmousi模型叠前时间偏移剖面

图3 Marmousi模型地下R点激发波场照明

1.2 能量方向性的确定

弹性能量在介质中的传播可以看做是弹性位能和动能的相互转化过程，系统中的弹性能量可以表示为(孙成禹，2007)：

(2)

式中，E为弹性能量，K为表征应力应变关系的介质弹性系数，ρ为介质密度，当我们研究声学介质时，p为标量声压场，V为速质点振动速度矢量场.

定义能流密度矢量I表示单位时间内通过与能量传播方向垂直的单位面积内的弹性能.根据能量守恒原理，

(3)

根据高斯定理，将面积分转化为体积分，同时考虑体积Ω的任意性，得到

(4)

对(2)式取时间微分，并结合运动平衡微分方程，得

(5)

因此，

I=pV,

(6)

即，在声学介质中，能流密度矢量等于标量声压场与矢量质点振动速度场的乘积，方向由质点振动速度方向决定.

在直角坐标系中，能流密度矢量的倾角θ和方位角φ表达为

(7)

其中V=vxi+vyj+vzk,θ是与Z轴正方向的夹角，φ是矢量I在XOY平面的投影与X轴正方向的夹角，由θ和φ就能确定空间任一点传播地震波的能流密度方向.当地震波传播到地表，θ和φ就是地震波在地表的出射角度.

图4(a,b)为图2所示R点激发，用一阶声波方程正演，在地表接收到的vx、vz分量模拟记录.Marmousi模型为二维模型，模拟结果中不存在vy分量，此时φ=0，θ不具有唯一性，不能用来准确刻画出射角度.重新定义一个角度α为能流密度矢量I与正X方向的夹角.为了计算的稳定性，统计出射角度的时候可以截取初至波的首周期计算，计算公式如(8)式所示，式中T1～T2为截取的时窗范围.

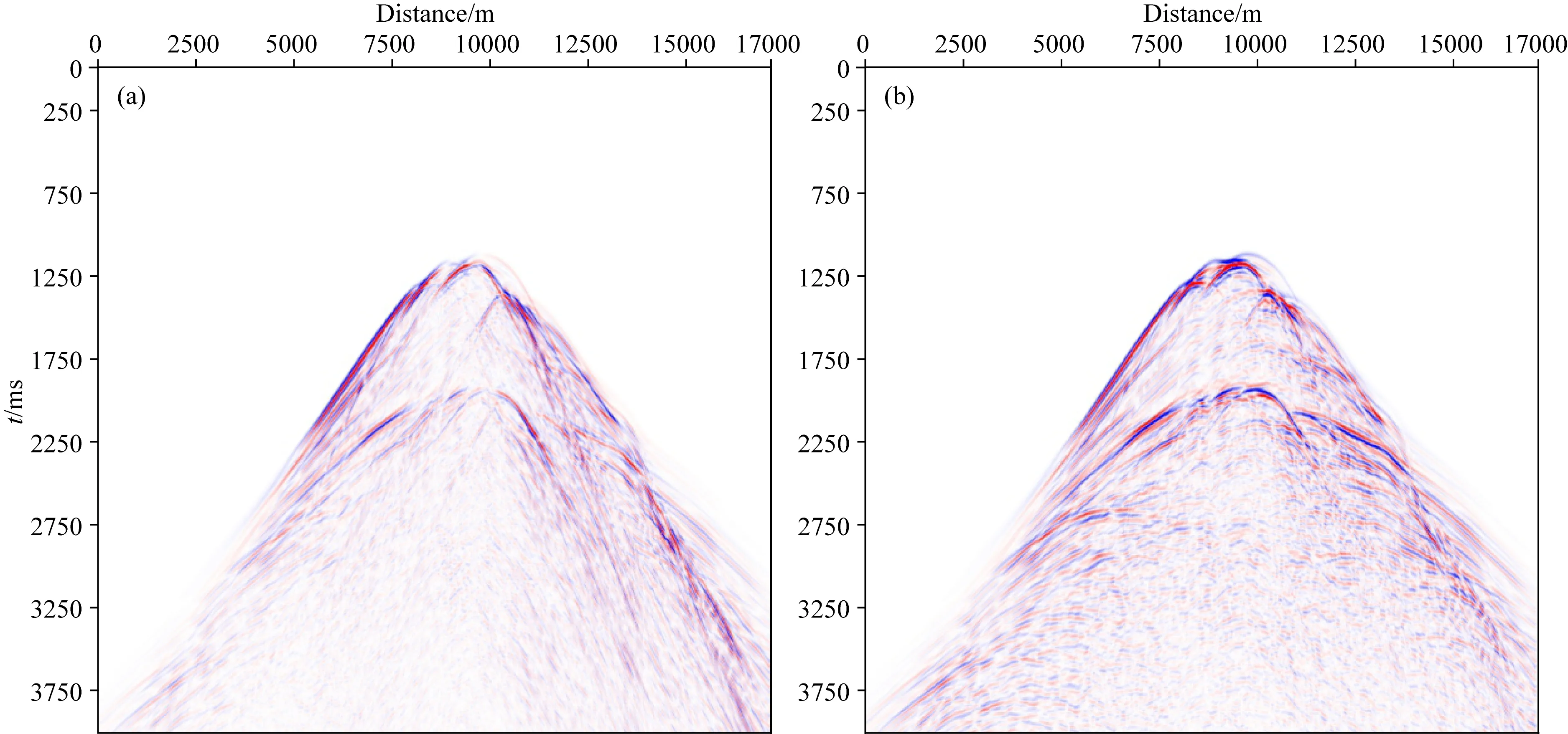
图4 地下R点激发地表接收到的vx(a)、vz(b)分量模拟记录

(8)

图5给出了依据公式(8)计算得到的出射角度α分布，可以看到在R点正上方附近地震波以90°出射地表，然后向两侧迅速改变；R点左侧地震波出射方向与X轴正方向相反，角度在100°～120°之间；R点右侧地震波出射角度由90°快速过渡到60°附近.对公式(6)取模，同样截取T1～T2时窗计算出射能量大小，得到图6.对照图3与图6，后者中的高幅值与前者中的“亮线”在地表位置能够一一对应.值得注意，模型的复杂性使地表相邻位置的出射角度和能量变化较大，曲线并不光滑，尤其是在R点上方区域，高陡的断层截断了能量的通路，使透射上来的能量断续展布.

图5的角度曲线给出了在地表做定向组合的方向，而图6的能量曲线则可以解答在何处布设定向组合才最有效.

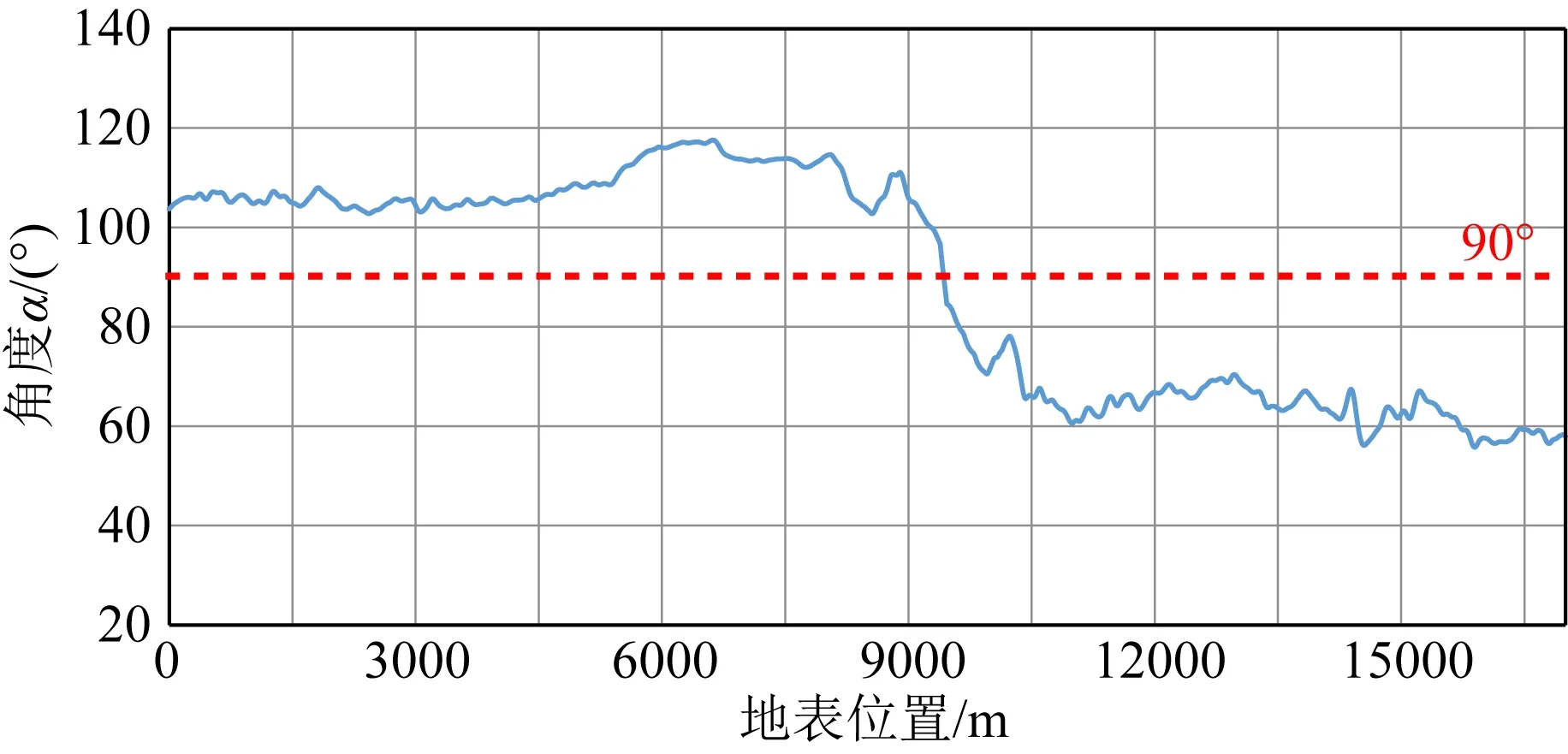
图5 地下R点激发在地表接收到的能流密度矢量与正X方向夹角

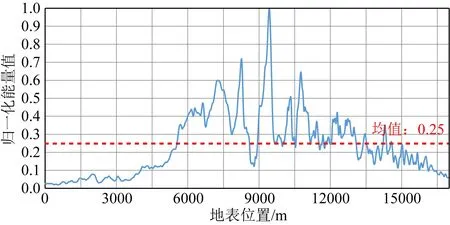
图6 地下R点激发在地表接收到的能流密度矢量大小

1.3 定向组合参数计算

在得到地下目标位置上传地表的波场角度和能量之后，下一步的工作就是要通过定向组合手段将震源激发的地震波聚焦为一个窄波束，将检波器的接收口径也聚焦为一个窄波束，使这两个波束的方向指向波场角度方向.下面以炸药震源组合为例介绍定向组合参数的设计方法.

组合过程为各震源子波的线性叠加过程.如图7，空间不同位置的几个震源Si发出的子波wi以v的速度传播了di的距离后在空间观测点P进行线性叠加.假定各震源的激发耦合性一致，激发子波的频率成份一致，子波振幅由炸药量决定(实际的情况更为复杂，为方便讨论暂且这样假设)，叠加子波表达为：

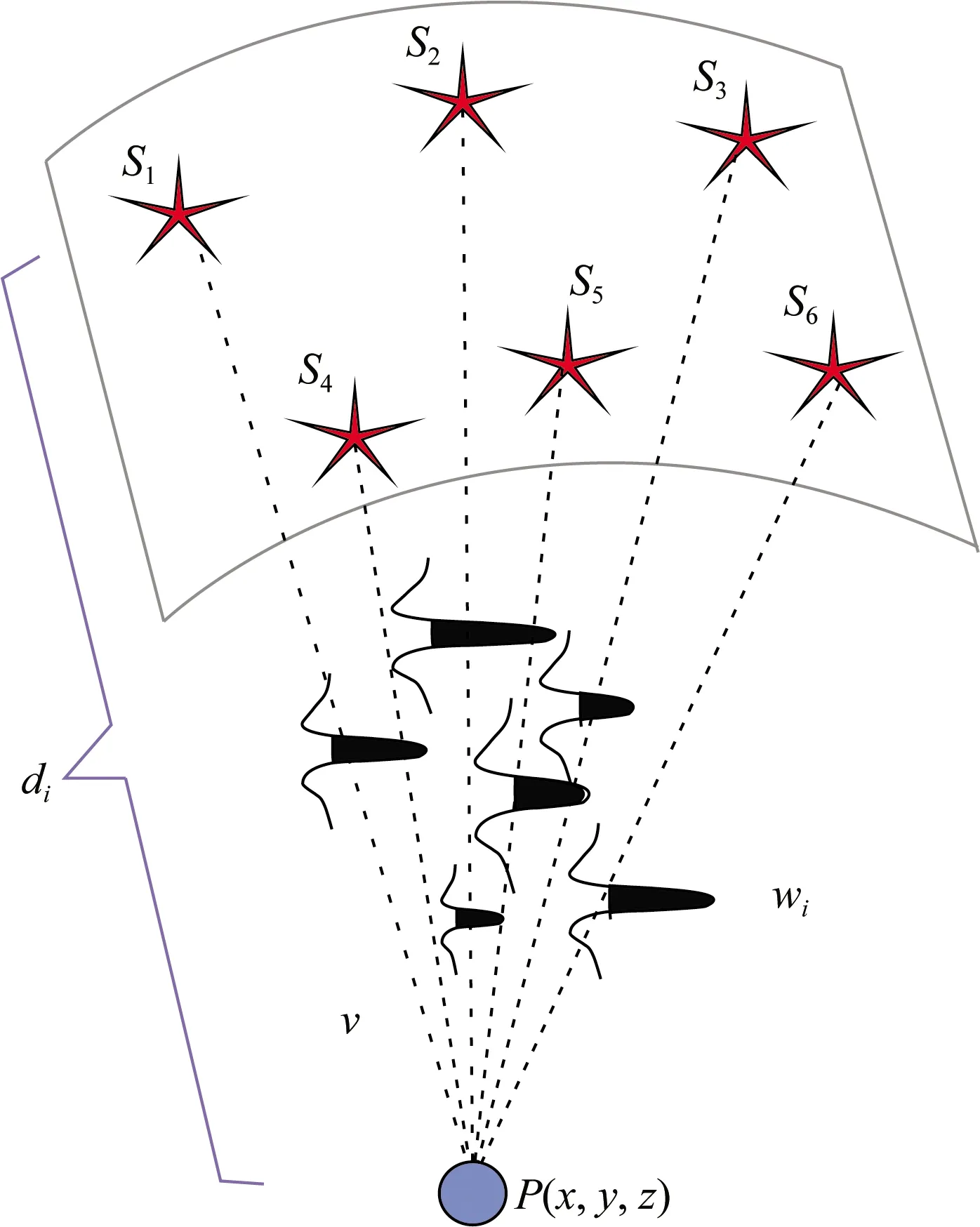
图7 震源组合示意图

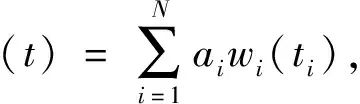
(9)

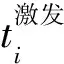
(10)

(11)

(12)

公式(9)给出了空间P点的叠加子波形式，随P点位置变化，叠加子波能量将发生改变，以震源的组合中心为圆心，P点位置为半径，绘制一个圆，利用公式(12)计算得到不同方向上的能量变化，这通常被称为能量方向因子(图8).若组合参数的搭配使得某方向上ti近乎相等，则在该方向上子波等相位叠加，能量达到最大，实现了聚焦；在该方向之外，相位相抵，能量不同程度被削弱，实现了能量压制，这是组合定向的基本原理.

图8a为某套组合参数下方向因子的三维空间展现，颜色值代表了归一化的能量大小，图中能量在斜向下的方向上实现了聚焦.图8b为图8a三维方向因子沿XOZ平面的二维切片(图中的参数1)，径向为归一化能量大小，环周为空间角度，图中同时给出了能够将能量聚焦到同一角度方向的组合参数2对应的方向因子以及能量理想聚焦情况下的方向因子.

理想的定向组合是将能量只聚焦在需要的方向上，其他方向不泄露，如图8b紫色阴影所示.而实际组合时因组合数目、组合间距、子波频率成分等因素的制约，往往在需要的压制区能量会有泄露，且越追求能量的聚焦性，压制区就会泄露越多的能量.如图8b中，相较于红色曲线，蓝色曲线在290°附近更加聚焦，但在其他需要压制的角度上能量幅值更大，定向性反而更差.因此做定向组合时不能一味的追求聚焦性.

考虑到用公式(8)计算的角度也会存在误差，实际设计定向组合参数时推荐使用一个角度区间来代替这个单一角度，这个区间由出射角度向两侧膨胀一个角度β来实现(比如待聚焦角度α=300°，采用β=10°，则聚焦区间设定为290°～310°).定义一个目标函数，使聚焦区间内的能量相较于区间外最大，作为设计组合参数的依据.

(13)

公式(13)的分子项代表聚焦区间内的能量，分母项代表聚焦区间之外其它部分的能量.式(13)是进行震源平面面积组合的参数求解目标函数，若只进行沿测线的线性组合，可以忽略φ的积分.检波器定向组合与震源组合原理一致，区别在于检波器接收的都是来自于地下半空间的信号，应用公式(13)的时候，分母中被减项θ的积分区间变为180°～360°即可.

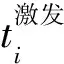
2 数值模拟

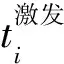
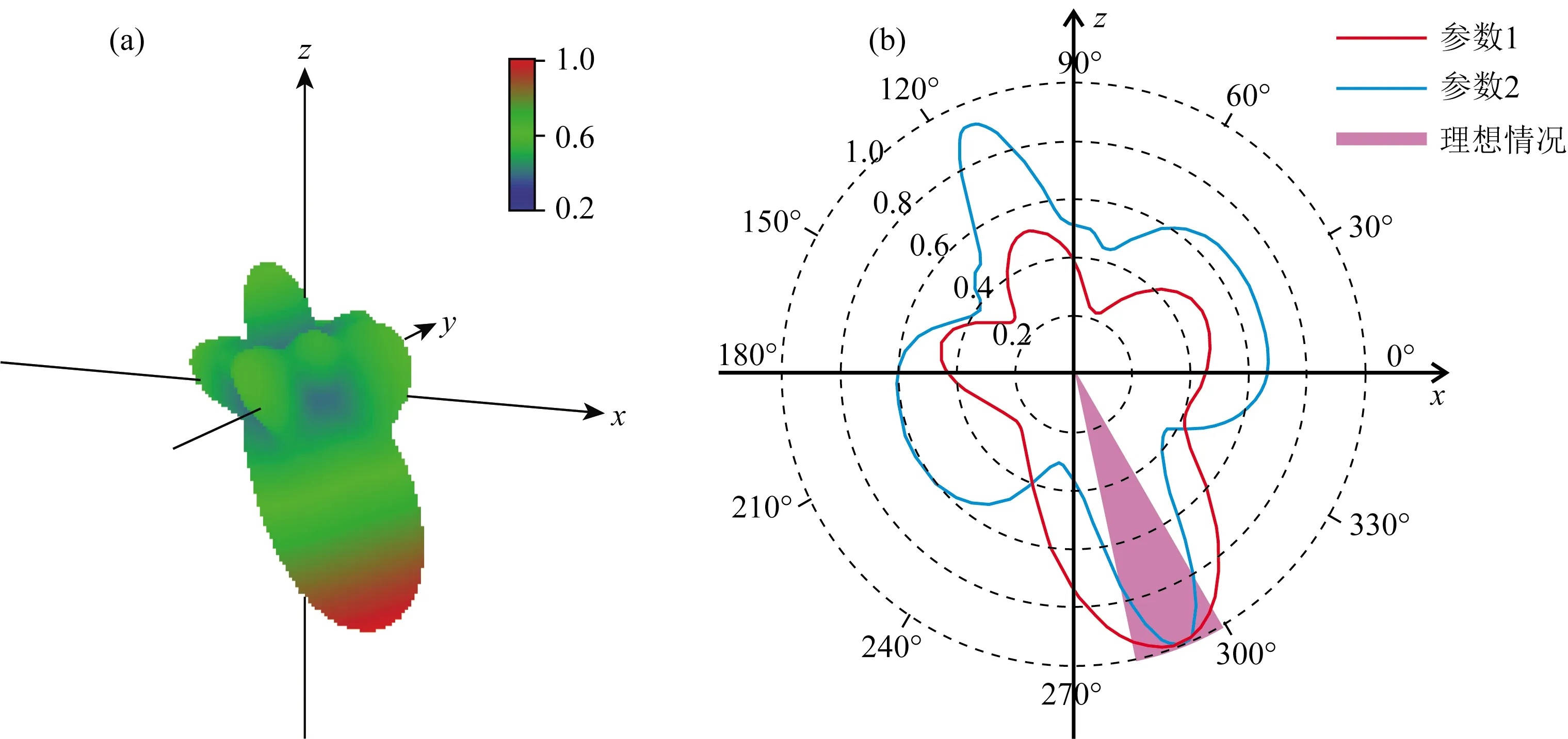
图8 能量方向因子图

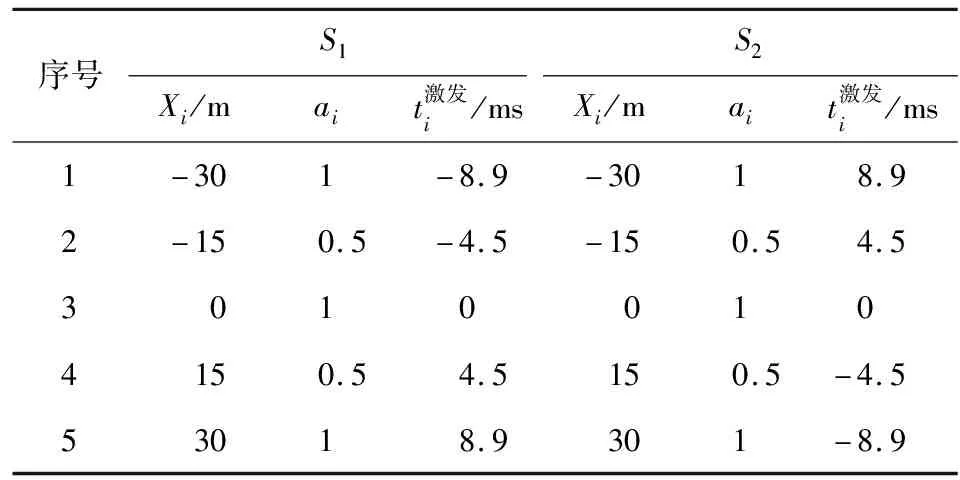
表1 S1、S2炮点定向组合参数

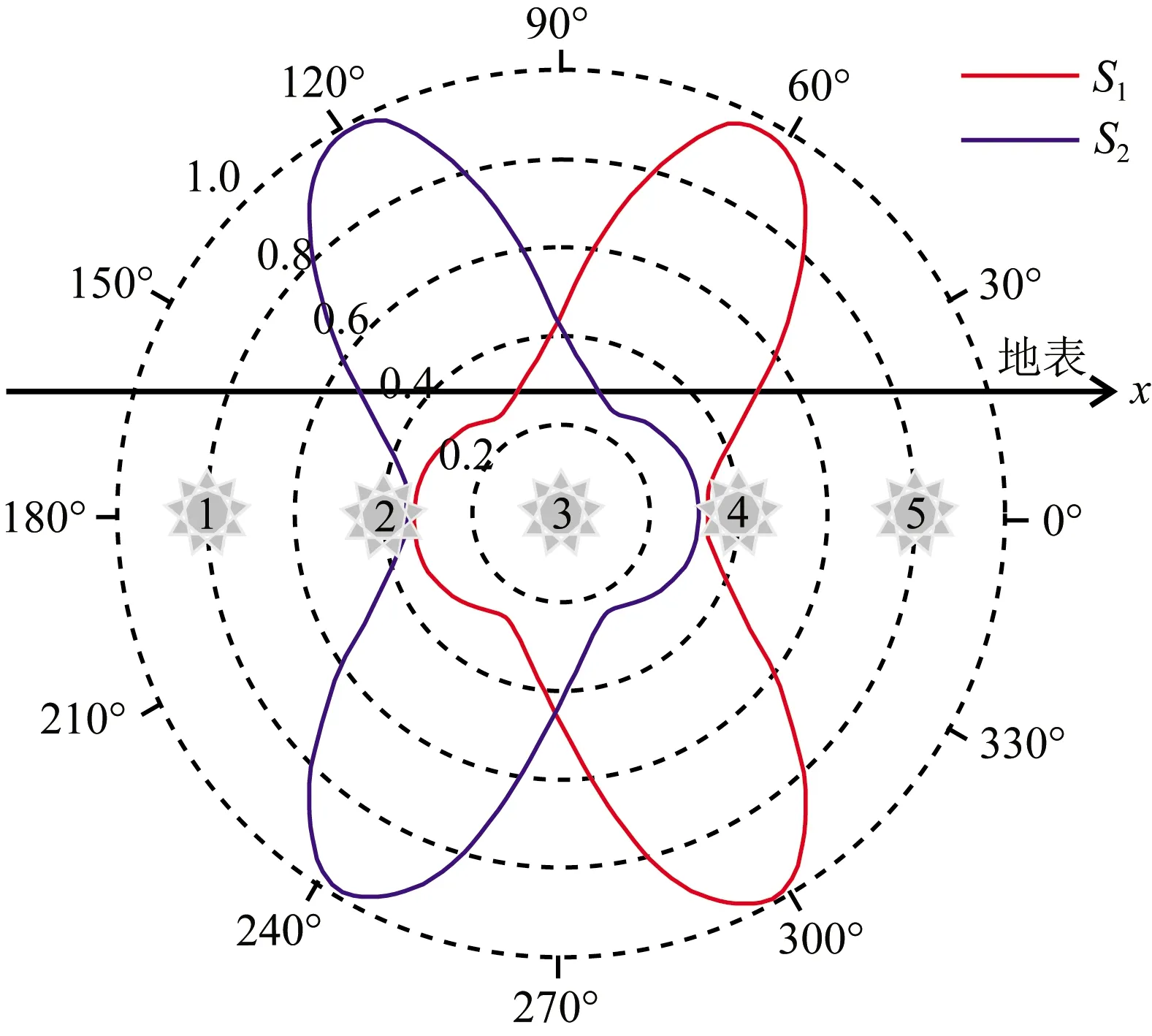
图9 S1、S2激发点定向组合能量方向因子

首先对S1、S2两个位置不组合进行单炮点激发照明，得到图10(a,b)，然后按照表1的参数进行炮点定向组合激发照明，图11a为S1炮点定向组合激发效果，图11b为S2炮点定向组合激发效果.对比二者，可以发现定向组合后波场能量在地表聚拢后以较窄的范围倾斜下传，在激发点与地下R点的通路上能量强度明显增强，至R点所在区域，照明强度较单炮点激发提升较大.

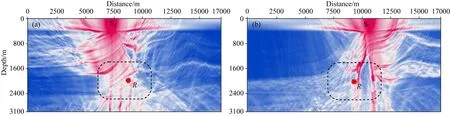
图10 Marmousi模型地表单炮激发照明

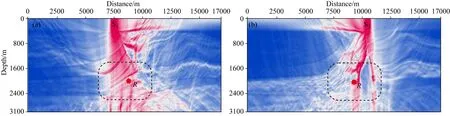
图11 Marmousi模型地表定向组合激发照明

参照图6，地表不同位置对R点区域照明贡献程度不一，选择能量贡献较大的位置进行定向组合更有实际意义，本文采用平均值方法确定待组合位置.对图6曲线取平均值，大于平均值的位置进行定向组合，其余部分单点激发不组合，同时保证组合激发时的总能量与单点激发的总能量一致，定向方向遵循图5计算结果.对组合后的数据处理得到叠前时间偏移剖面(图12)，对比图2，高陡断层下方区域的成像效果明显改善，验证了该方法的有效性.

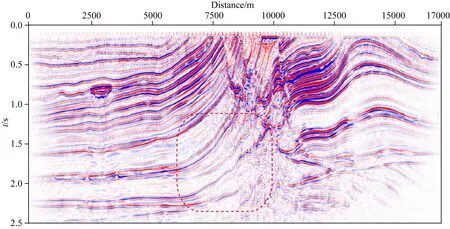
图12 应用了定向震源组合激发的Marmousi模型叠前时间偏移剖面

3 工区实例

塔里木盆地塔西南工区表层巨厚黄土覆盖，地表高程起伏较大，黄土下方覆盖一层第四系砾石，砾石层下伏老地层由于构造运动倾角普遍较大，砾石与老地层间呈角度不整合关系，高速层与低降速层间的地震波阻抗差较大，工区的地质特征非常不利于采集到高质量的地震资料，工区典型地表地貌如图13所示.2019年，塔里木油田在该工区进行了一条线束地震采集作业，目的在于落实工区**段南北向断裂地质构造.为提高采集资料品质，现场采用了较密的空间采样，采集炮点距30 m，炮线距30 m，检波点距15 m，接收线距30 m，采用26线4炮960道奇偶观测系统，覆盖次数达到了960次.结合前期的采集试验分析，震源采用3口Inline方向线性组合，组内距5 m，激发药量3×8 kg，检波器采用3 m×7.5 m组内距的20支矩形组合模式.观测系统及野外震源、检波器组合形态见图14(a,b).

图13 塔西南工区典型地表地貌

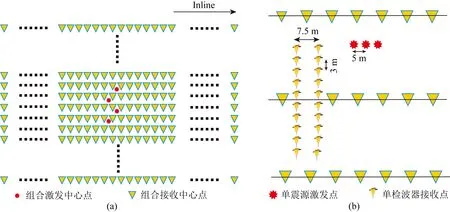
图14 工区采集观测系统及野外震源、检波器组合形态

虽然在野外已经采用了组合激发、组合接收的方式，但受限制于极差的地表条件，采集单炮质量不高.极低信噪比的资料，复杂的构造形态，较高的空间采样密度，为应用定向组合技术提供了有利条件.

本文采用的地质模型来源于测线第一轮处理解释成果，如图15所示.组合处理目标为加强模型中部隆起断块的成像质量.

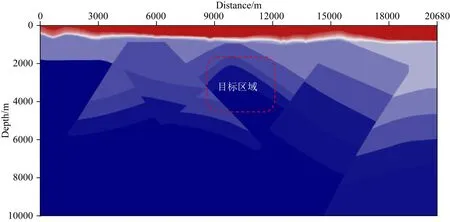
图15 工区初轮解释模型

按照前文所述的技术思路，首先对地下目标区域进行炮点向上波动方程照明，如图16所示，统计地表接收的角度和能量，叠合显示在照明图上方.图中可以看到出射能量主体分布在隆起断块的地表位置两侧，右翼地层倾角较左翼平缓，接收能量更强；出射角度主体受控于构造两翼地层倾向和倾角大小，同时被表层黄土的非均质性复杂化，左翼均值110°左右，右翼波动较大，在黄土较厚的山体部位波场以近90°出射地表.

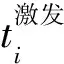
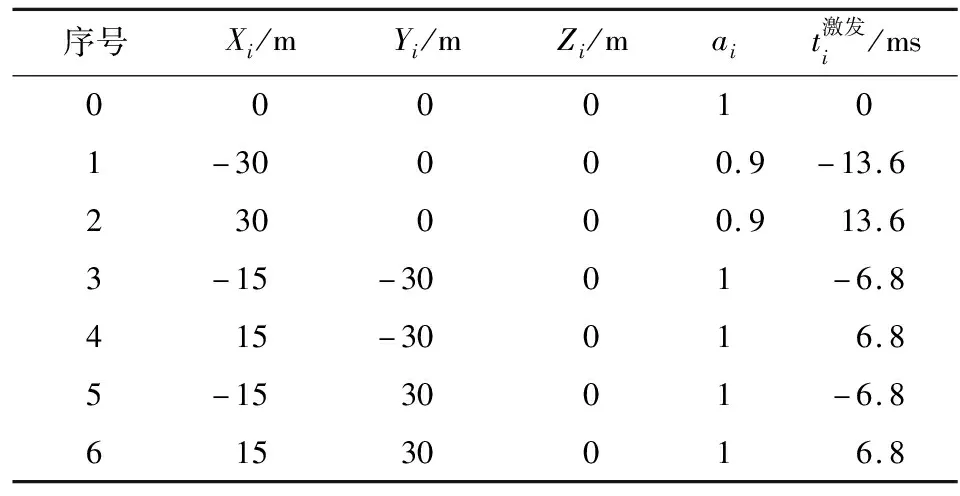
表2 A点震源定向组合参数

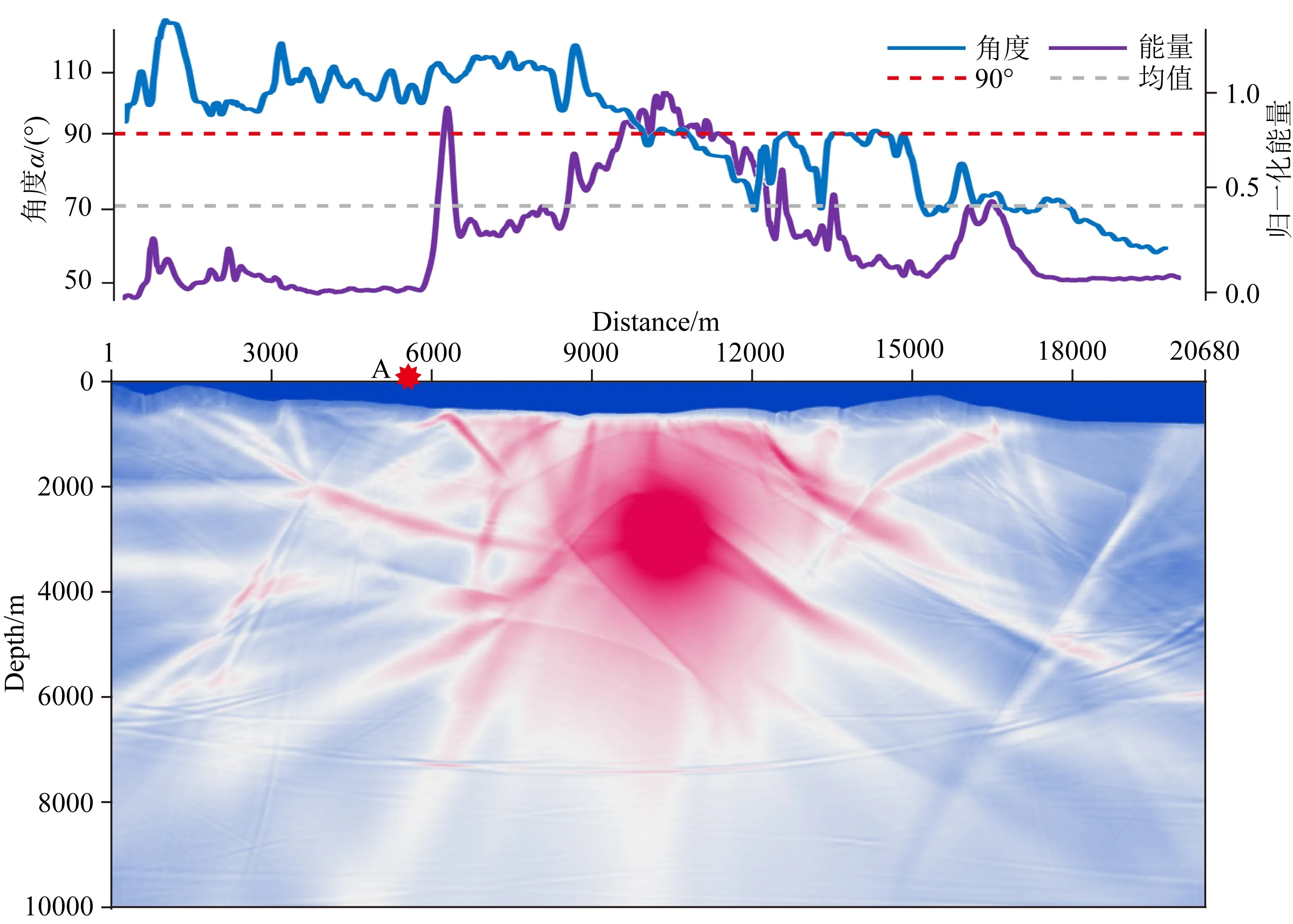
图16 地下目标体向上激发波场照明

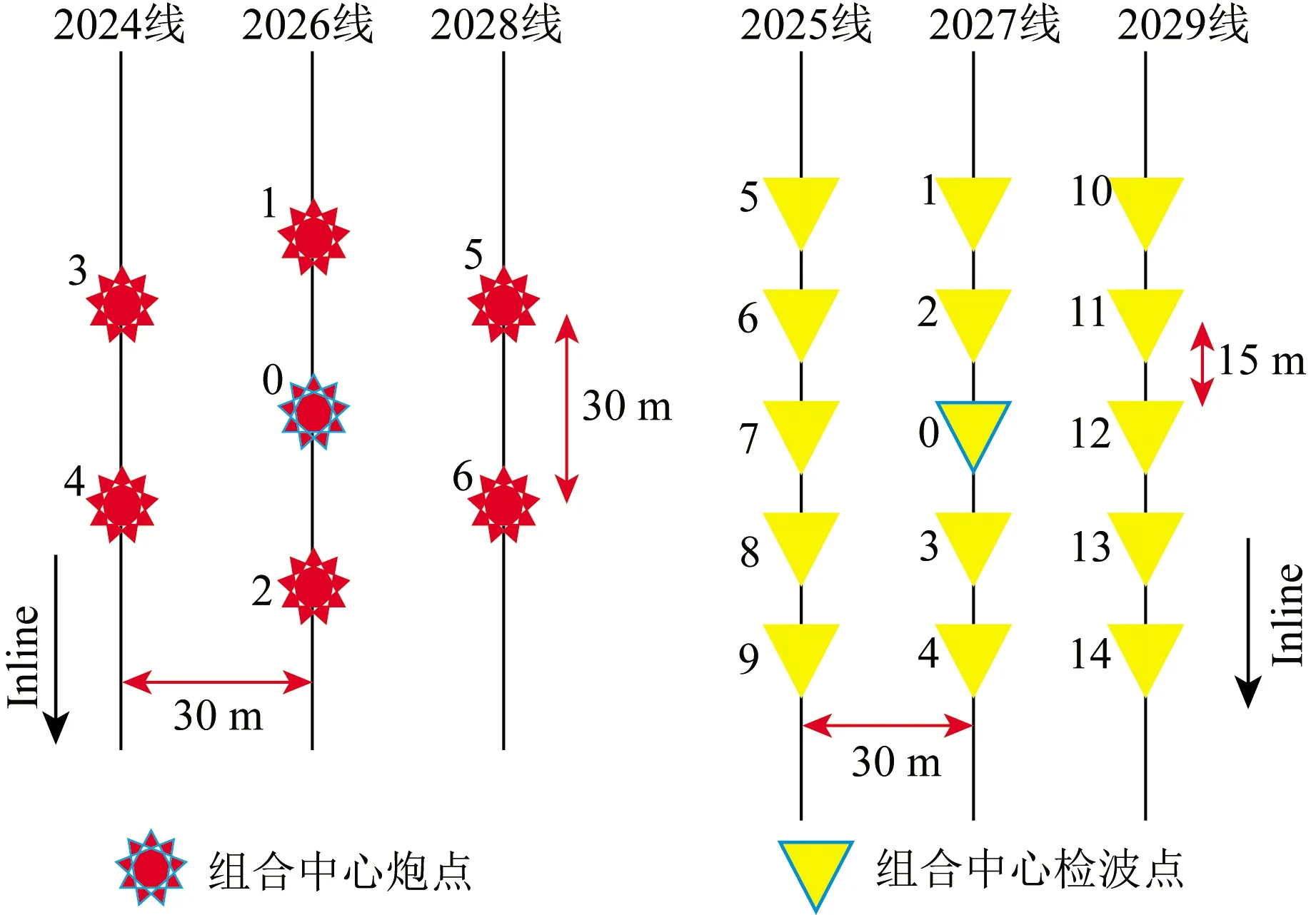
图17 震源与检波器组合形态示意图

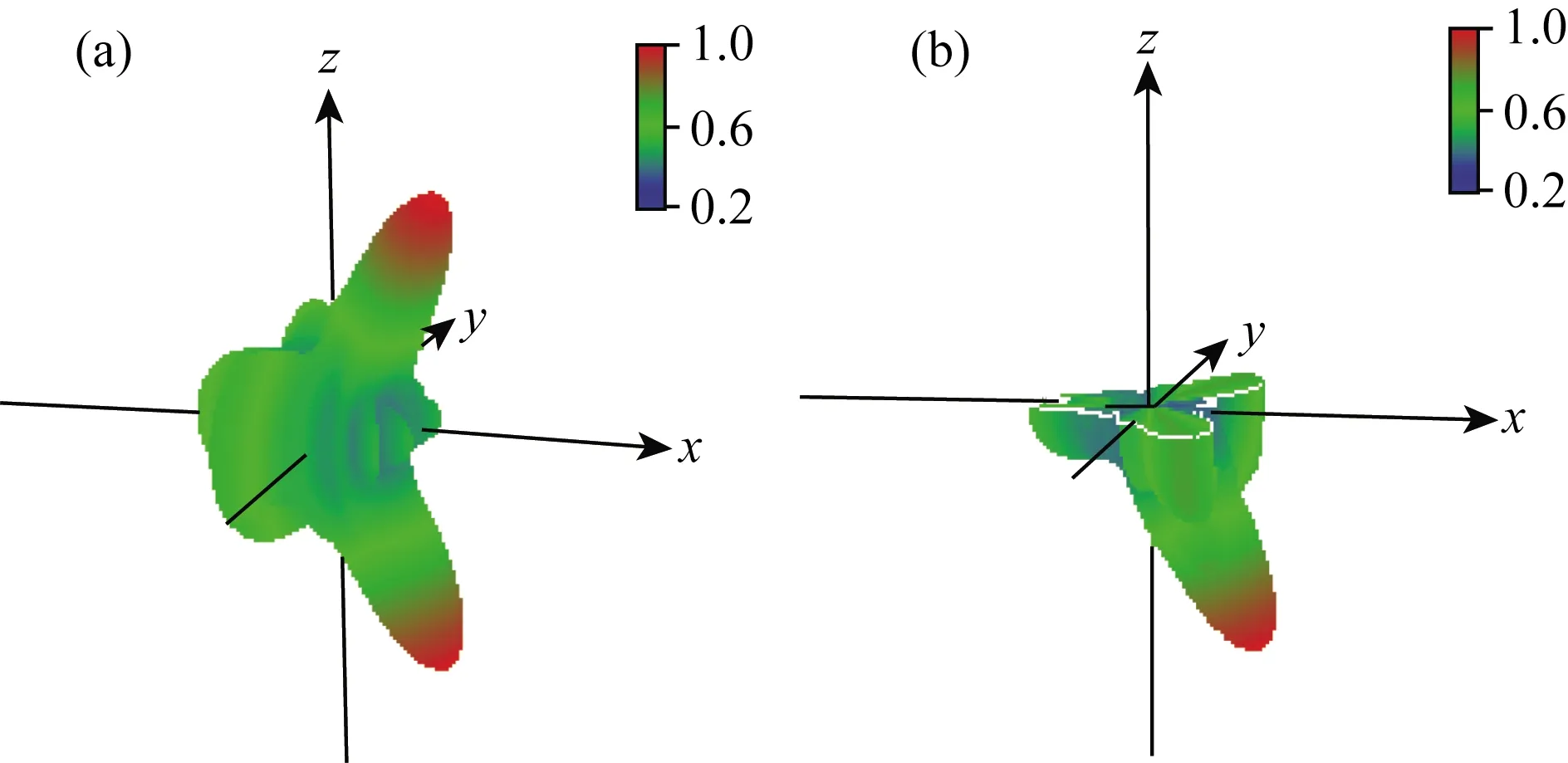
图18 震源与检波器定向组合能量方向因子图

对实际数据的组合处理结果见图19，显示的CMP点位于目标区域的地表投影位置.图19a为原始采集数据，可见信噪比很低，记录中隐约能看到反

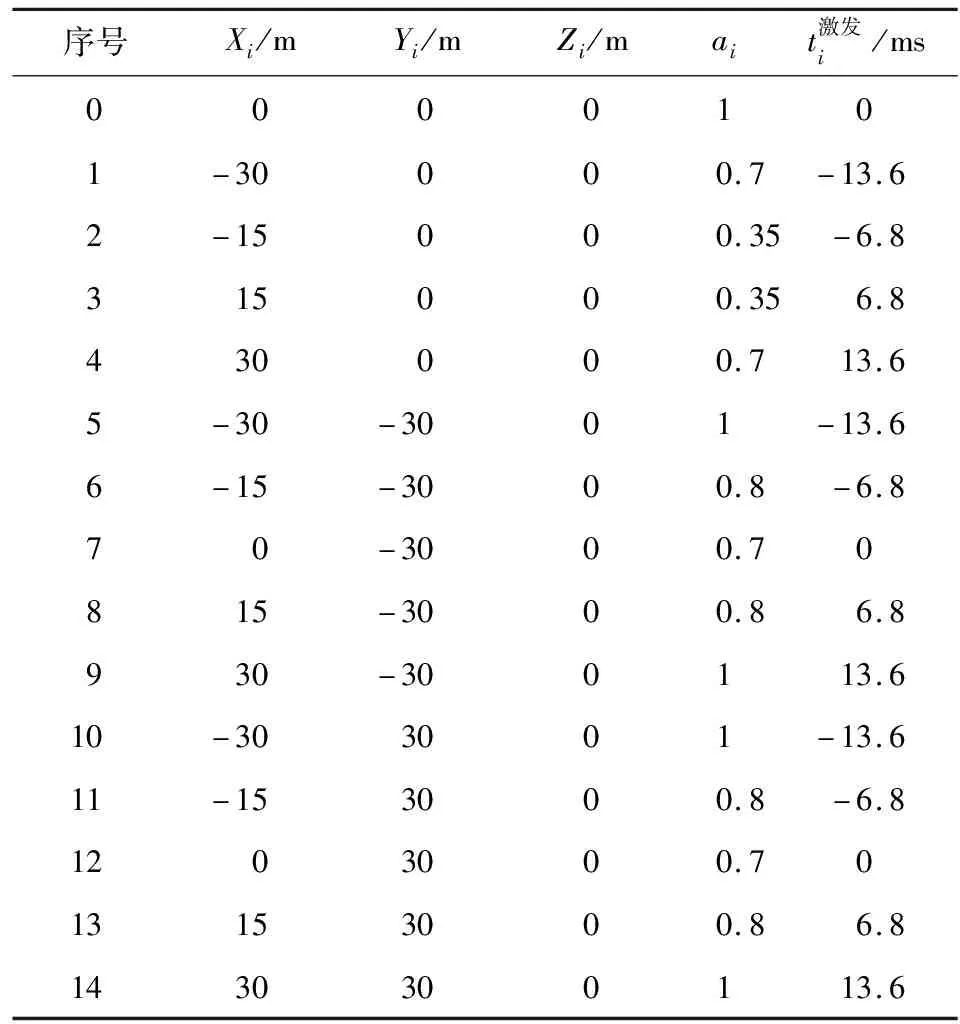
表3 A点检波器定向组合参数

射轴的“影子”，但被强噪声覆盖；图19b为单独采用震源端的炮点定向组合结果，在500 ms、1000 ms、1500 ms、2000 ms，甚至更深层的3000 ms时间附近，地层反射同相轴连续性明显加强；图19c为单独应用检波端的道间定向组合结果，反射轴改善效果更加明显，且记录整体噪声压制明显；图19d为综合运用炮-检联合定向组合方案的效果，与图19a原始数据相比较，信噪比改善明显.工区应用实例说明本文提出的方法对极低信噪比地区叠前数据的品质改善有效.

图20展示了应用炮-检联合定向组合前后的水平叠加剖面，为突出对比组合效果，除静校正、速度分析、水平叠加外，未做任何去噪、提分辨率处理.取图20a中的窗1左半侧与图20b中的窗1右半侧数据拼接成图21a，以清晰呈现组合前后的对比效果，图21b做法类似.观察组合前后的两张剖面，很明显经定向组合处理后目标层位整体成像效果更好，地层同相轴的连续性得到了增强.在1000 ms以上的浅层改善效果尤为明显，这与图19中的叠前记录效果改善能够相互印证；在中深层，定向组合压制了随机噪声，强化了被复杂构造遮挡的下方地层成像.叠加剖面的实例进一步说明本文提出的定向组合方法对改善低信噪比地区叠加数据的成像质量有效.

图22(a,b)分别给出了应用炮-检联合定向组合前后的叠前记录(图19)和叠加剖面(图20)的频谱分析结果，可见组合之后频带宽度有一定程度的收窄，这是由组合本身的频率滤波特性决定的.图中20 Hz之前几乎没有变化，30 Hz～100 Hz之间存在5 dB的能量衰减，衰减趋势比较稳定，这部分频率的能量损失可以考虑在后续处理中采用Q补偿、反褶积等手段予以弥补.

图19 定向组合前后的叠前记录(CMP道集)

图20 定向组合前(a)、后(b)水平叠加剖面

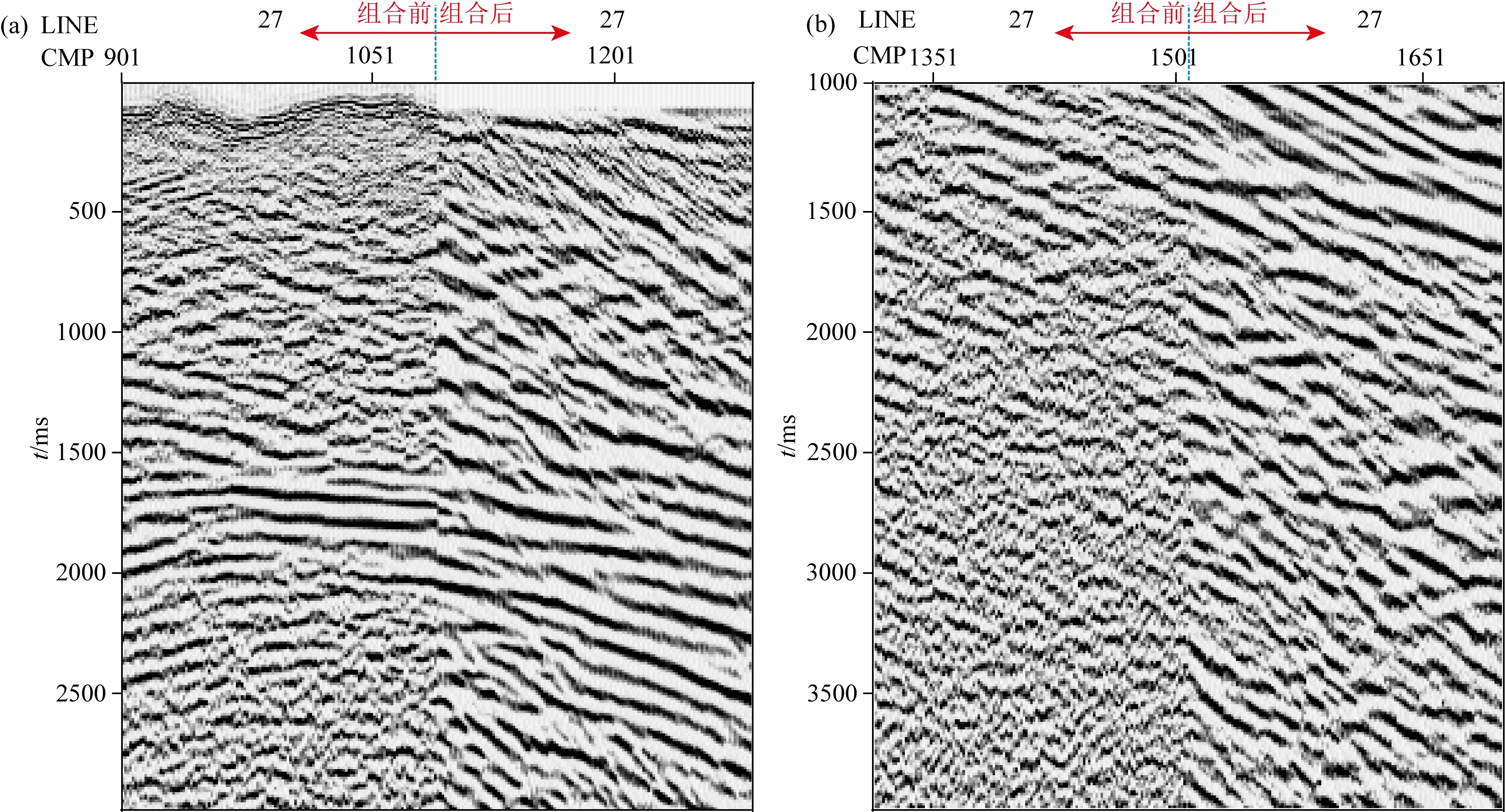
图21 定向组合前、后水平叠加剖面(局部放大)

4 结论与认识

本文分析了地震波场定向传播的机理，推导了地震波在地表位置的出射角度和能量大小，给出了利用组合技术实现地震波定向聚焦的计算方法，经Marmousi模型理论验证和工区采集数据实例验证，证明基于模型的定向激发/接收技术能有效改善低信噪比地区的地震资料品质.研究过程得出如下结论：

(1)地震波在地下传播是有方向的，方向性与地质结构相关，由地层倾角、弹性参数等因素决定，地质结构越复杂，方向差异性越大；

(2)空间任意位置处的地震波场方向和能量可以通过能流密度矢量定义，在声波介质中，该矢量方向同质点震动速度矢量方向一致，矢量大小由质点声压场值和质点速度场模量乘积决定.在地下某位置激发，计算波场传播至地表的能流密度矢量，可以用来确定进行定向组合的角度和组合位置；

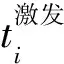
(4)通过基于模型的激发-接收定向组合，能够明显提升叠前数据信噪比，改善叠加剖面成像质量.

需要指出，本文展示的图片只进行了一个轮次的组合试验，由于地表的复杂性、地下目标模型的准确性等因素，无法保证计算能流密度矢量的完全准确，这将导致组合定向出现一定误差，降低信噪比的改善程度，对资料的频谱也会有一定的损伤.更为合理可靠的方式是多轮迭代逼近，即在经本文定向组合，成像质量改善的成果剖面基础上重新解释，对地质模型迭代更新，用新模型再次完成定向组合处理，视剖面质量改善程度决定退出迭代还是继续再下一轮次的更新.

致谢本文受中国石油集团公司重大科技专项课题“复杂山地、黄土塬及大沙漠区地震关键技术研究与应用”(2018E-1807)的支持与资助，同时，感谢国家自然基金项目“炸药震源在不同岩性中激发生成弹性能量的数值模拟”(41804137)对本项目研究的资助.