一维动静组合加载下多角度耦合充填体力学特性研究

陈 超 杨志彬 马姣阳 李洪宝 张 震

（1.华北理工大学矿业工程学院，河北唐山063210；2.河北省矿业开发与安全技术重点实验室，河北唐山063210）

经济、安全、高效、环保是现代化矿山的标志，以高阶段、大尺寸空间为特征的嗣后充填采矿方法应用日益广泛［1-3］，然而在嗣后充填二步回采时充填体矿柱不可避免地受到爆破扰动，如不加以控制必将影响采场安全，因此开展充填体力学特性研究对于实现安全高效二步回采具有重要意义［4］。

目前，国内学者对充填体力学特性开展了大量试验研究，张钦礼等［5］通过制备高密度全尾砂胶结充填体（HTB）试件，采用SHPB以不同速度冲击HTB试件，测得HTB试件在应变率10～305 s-1范围内动态稳定性，并分析认为HTB试件稳定性与应变率密切相关。杨伟等［6-7］利用SHPB试验装置测定了高应变率下（103.1～265.5 s-1），高浓度全尾砂胶结充填体的动态力学性能，但其制备的试件较少，结果离散性大。朱鹏瑞等［8］通过不同应变率下SHPB单轴冲击试验，得到了冲击荷载下维持分级尾砂宏观稳定形态的最高应变率及充填体在较高应变率条件下的应力—应变曲线。谭玉叶等［9］采用SHPB试验装置开展了胶结充填体单轴循环冲击试验，研究了充填体在未完全宏观破坏的冲击速度下多次循环冲击的应力应变、动载强度及变形破坏特征。以上研究虽然已注意到充填体在开采过程中受到爆破扰动的现状，但未考虑到充填体在受到爆破扰动之前所处的受力状态，事实上，在深部充填回采过程中，充填体矿柱在受到爆破扰动之前就已承受一定的地应力或静应力，此时受到爆破扰动属于典型的充填体动静组合加载问题。然而，目前国内针对动静组合加载下充填体力学特性的研究较为薄弱，张云鹏等［10］在利用SHPB冲击之前，通过预先施加轴压反映出了这种受力状态，并开展了不同应变率动静组合加载下的充填体动力学特性研究，得到了高浓度下充填体破坏模式，但并未反映出较小应变率及冲击波经过不同传递路径作用于充填体时的破坏机理，并且近年来在耦合充填体方面的相关的成果也鲜有报道。本研究以多角度耦合充填体试件为分析对象，选取3个轴压水平，开展不同应变率下SHPB单轴冲击试验，研究动静组合加载下充填体强度特征、变形特性、破坏机理及冲击波衰减规律，为深部充填二次回采过程中充填体矿柱稳定性分析及安全评价提供理论基础。

1 试验研究

1.1 试件制备

（1）试验原料。某矿超细尾砂中值粒径d50=14.56 μm，超细尾砂粒级组成曲线见图1。此外，试验原料还包括325#普通硅酸盐水泥、花岗岩、水等。

（2）制备过程。首先选用完整性和均值性较好的花岗岩，经钻取切割打磨得到φ50 mm×25 mm圆柱岩石试件及φ50 mm×50 mm的45°斜面岩石试件，制备耦合体。

试验试件尺寸为φ50 mm×50 mm，灰砂比1∶8，质量浓度为68%，采用1∶1耦合。根据设定的灰砂比及浓度参数计算称量出所需尾砂及水泥材料，置于搅拌桶内均匀搅拌，之后在φ50 mm×50 mm圆柱形模具中进行浇筑。耦合体浇筑时，先将岩石置于底部，再浇筑料浆，24～48 h后脱模并置于HY-40A养护箱养护14 d。待养护完成后，对试件上下表面进行打磨处理，经打磨处理后绝大多数耦合体试件仍然互相结合。对于部分充填体和岩石互相分离的耦合体试件，在试验过程中将黄油涂抹于试件端部进行人工耦合，经轴向加压后试件整体耦合度较高。打磨后的充填体如图2所示。

1.2 SHPB试验设备

冲击试验采用分段式SHPB装置（图3），该装置是研究材料动态力学性能的最佳设备［11-12］，可精确记录试件冲击破坏时动态力学参数［13-14］。系统导杆采用高强度45GrNiMoVA合金钢，直径50 mm，纵波波速为5 200 m/s，密度为7 800 kg/m3。子弹头、入射杆、透射杆杆长度分别为0.36、2.00、1.50 m。采用超动态应变仪采集数据并用DL-750示波器显示波形，计时设备采用JXCS-02型计时仪。

1.3 动静组合系统原理

本装置采用纺锤形的异形子弹头以减少PC振荡达到半正弦应力波恒应变率加载［15］，SHPB原理如图4所示。

因此，试验中通过超动态应变记录到的入射信号和透射信号，便可计算出试件的应力σs(t)、应变εs(t) 和应变率

2 试验结果分析

2.1 冲击试验强度分析

冲击试验前，测得静载下充填体试件的力学参数如表1所示。

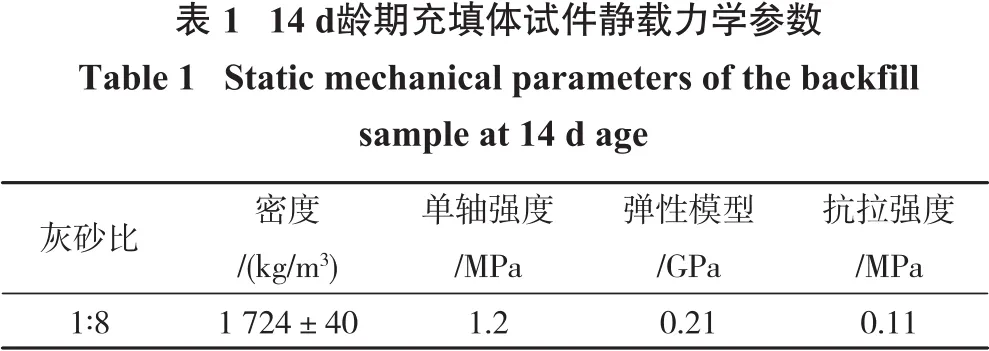
本研究定义的动态强度增长因子为

式中，σc为动载下充填体抗压强度，MPa，σj为静载下充填体单轴抗压强度，MPa。

充填体试件的冲击试验数据取值见表2。

图5为相同轴压不同应变率下的充填体动态强度增长因子变化特征，轴压分别为0、0.48、0.96 MPa。从图中可看出：常规冲击（轴压0 MPa）时，充填体动态抗压强度随应变率增大而增大，两者相关性较高。当应变率较小时（ε˙=17 s-1左右时），动态强度增长因子K为1.6左右；随着应变率增大（ε˙=35 s-1左右时），动态强度增长因子K为2.1左右；当应变率升至58s-1左右时，动态强度增长因子K也增大至2.6左右。动静组合加载轴压保持不变时，充填体动态抗压强度也随着应变率增大而增大，该变化规律与常规冲击时基本一致，同时表明充填体动态抗压强度并非随轴压增大而线性增大，存在最优轴压值使得充填体动态抗压强度达到最佳。

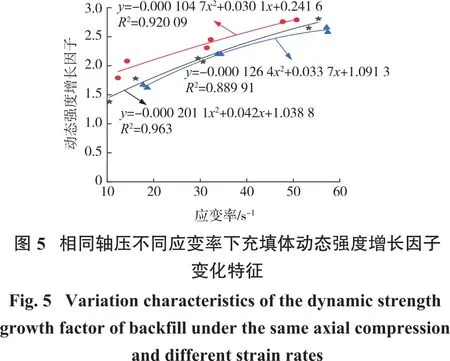
不同轴压相近应变率下充填体的动态抗压强度变化特征如图6所示。由图6可知：相近应变率下增大轴压，充填体动态抗压强度呈现出先增大后减小的趋势，最大动态抗压强度在轴压为静载强度40%（0.48 MPa）处。当轴压施加值较小时，充填体内部微裂隙逐渐闭合，在此基础上进行轴向冲击，降低了反射波的拉伸作用，使得充填体的劣化在一定程度上得到抑制，因而其动态抗压强度有所增强；当施加的轴压为静载强度80%时，轴压的施加使得充填体在裂隙完全闭合的基础上重新形成大量微裂纹，施加冲击荷载后，应力波在裂纹处形成的反射波，进一步加剧了裂纹贯通破坏，使得动态抗压强度有所降低；若进一步增大轴压，会使得充填体内部在冲击之前形成较大贯穿裂纹，此时仅需较小震动便可使充填体产生失稳破坏。

在深部嗣后充填回采过程中，对充填体矿柱稳定性影响最为显著的因素为矿柱宽度、矿房宽度和矿柱抗压强度［16］。当矿柱宽度和矿房宽度保持不变时，过大轴向静应力的存在极有可能使得充填体矿柱内部形成较大贯穿裂纹，造成抗压强度急剧下降，此时轴向爆破扰动便是造成充填体矿柱崩塌的主要影响因素。因此在深部嗣后充填回采过程中应注意选取较为合理的爆破安全警戒线，避免使得充填体矿柱受到较大的爆破扰动。

2.2 一维动静组合加载下充填体变形特性

图7为相同动载不同轴压下的充填体应力—应变曲线，可见，冲击荷载下充填体应力—应变曲线主要分为弹性阶段（OA）、屈服阶段（AB）、破坏阶段（BC），无明显密实阶段。常规冲击（轴压0 MPa）时，充填体可迅速密实变形，在动静组合加载时，提前施加的轴压使充填体内部微裂隙得到闭合密实，因此，在冲击荷载下充填体应力—应变曲线中微裂隙密实阶段并不明显。

在弹性阶段，动静组合加载下充填体弹性模量呈现出先增大后减小的趋势，在施加的轴压为静载强度40%处达到最大。说明在轴压0.48 MPa时，充填体内部微裂隙、气泡等在受冲击之前被压缩闭合，得到强度硬化，因此弹性模量有所增大；当轴压进一步提升至0.96 MPa时，充填体内部微裂隙在完全闭合的基础上开始产生内部损伤，新微裂隙开始产生及扩展贯通，使得弹性模量较之前有所下降，但由于并未产生较大贯通裂隙，故当施加的轴压为静载强度80%时，仍大于无轴压作用时的充填体弹性模量。

在屈服阶段，应力—应变曲线有小范围波动，出现多个小波峰，不同于岩石等脆性材料较为平滑的应力—应变曲线。当施加的动载较小时，无论轴压施加与否，曲线均为先达到峰值应力后再下降波动，这是由于所施动能较小且未达到最大抗压强度就已卸载造成的；当施加的动载较大时，较大能量的冲击使充填体动态强度瞬间得到硬化［7］，因此屈服阶段先达到一个应力波峰后，试件产生小规模破坏，应力下降，同时靠近透射杆的充填体部分内部裂隙进一步闭合压密，应力出现上升至峰值强度后逐渐卸载的现象。

2.3 一维动静组合加载下充填体破坏模式

无轴压时不同应变率下充填体破坏形态如图8所示。分析该图可知：常规冲击时充填体破坏模式为劈裂拉伸破坏，裂纹多沿轴向出现（18.63s-1），这是由于泊松效应使充填体产生横向拉伸及冲击应力波的纵向劈裂造成的。当应变率由18.63s-1逐渐增大至34.66、61.71s-1时，充填体的破碎程度逐渐增大，块度逐渐减小，在不同的应变率作用下，呈现出不同的破碎状态。

图9为相近应变率不同轴压时充填体破坏形态，图10为相近应变率不同轴压时0°耦合体破坏形态，图11为45°耦合下纵波透反射及冲击效果。

图9中施加轴压0.48 MPa时产生了“X”形大块，施加轴压为0.96 MPa时产生了圆锥形小圆台，分析可知，在轴压作用下充填体的破坏模式为剪切破坏；图10中施加轴压0.48 MPa时耦合体产生了圆锥形小圆台以及图11中产生了剪切裂纹，分析可知在动静组合加载下，无论冲击波直接或经岩石间接传递至充填体时的破坏模式均为剪切破坏。

当冲击波水平入射至充填体时，轴压的施加使得试件与导杆接触处的黄油挤出，导致试件两端产生端部效应，产生应力集中出现微裂纹，继续增大轴压，两端部微裂纹在内部裂隙气泡闭合的基础上，继续向内部扩展形成潜在的剪切破坏面，之后由于冲击加剧破坏面扩展形成”X”形及圆锥形小圆台，呈现出剪切破坏特征，轴压施加的大小对充填体破坏程度有较大影响。

当应力波垂直入射到Y平面时只产生反射纵波，而当其斜入射至Y平面时，将同时反射纵波与横波［17］。可以看出，当冲击波斜入射至充填体内时，由于反射横波的存在造成剪应力出现形成剪切破坏。

3 一维动静组合加载下充填体力学特性数值模拟

由于物理试验中难以测得冲击波在充填体内的衰减规律，故本研究以单一充填体为例，通过数值模拟方式，从波阻抗角度出发，对冲击应力波在充填体内的衰减规律进行分析。

3.1 模拟方法及参数确定

采用ANSYS/LS-DYNA建立模型，LS-PREPOST软件进行后处理。选用适用于高应变率、大变形问题的HJC模型，该模型常用于模拟混凝土、充填体等冲击破坏，证明具有较好的模拟效果。通过物理试验并结合相关成果［18-20］，充填体试件的HJC参数见表3。

注：ρ为材料密度；G为剪切模量；fc为准静态单轴抗压强度；A为特征化黏性强度；B为特征化压力硬化因子；C为应变率影响系数；N为压力硬化指数；Smax为特征化最大强度；T为准静态单轴抗拉强度；Pc为压溃点的压力；μc为压溃点的体积应变；p1为压实应力；μ1为压实体积应变；k1为压力常数；k2为压力常数；k3为压力常数；D1为损伤常数；D2为损伤常数；EPSO为参考应变率；FS为失效类型；εf，min为压碎塑性应变。

3.2 模型构建

选用SOLID164实体单元并通过映射网格划分为若干六面体单元，之后进行精细网格划分。杆和试件选取ASSC接触并采用0.1罚因子值，采用Lagrange算法进行显示结构处理分析，不考虑杆与试件的界面摩擦，最终构建的实体模型如图12所示。

3.3 模拟破坏形态分析

由于ANSYS语言不可直接设置应变率大小［8］，故由试验数据测得的冲击速度模拟不同应变率下破坏形态，冲击速度为4、5、6 m/s对应的冲击荷载分别为0.3、0.4、0.5 MPa。

以冲击速度v为5 m/s、轴压为0 MPa为例，在LSPREPOST软件中选取冲击后充填体前、中、后各3个单元点，得出试件表面9个单元模块上的真实应力—应变数据并导出。本研究以编号为2-2组为例，在Origin软件中绘制了模拟所得与试验所得的应力—应变曲线对比图，如图13所示。分析图13可知：模拟所得的应力—应变曲线与试验曲线基本吻合，无较大量级差异，说明模拟较为合理。

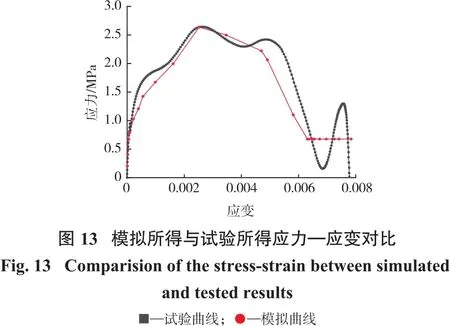
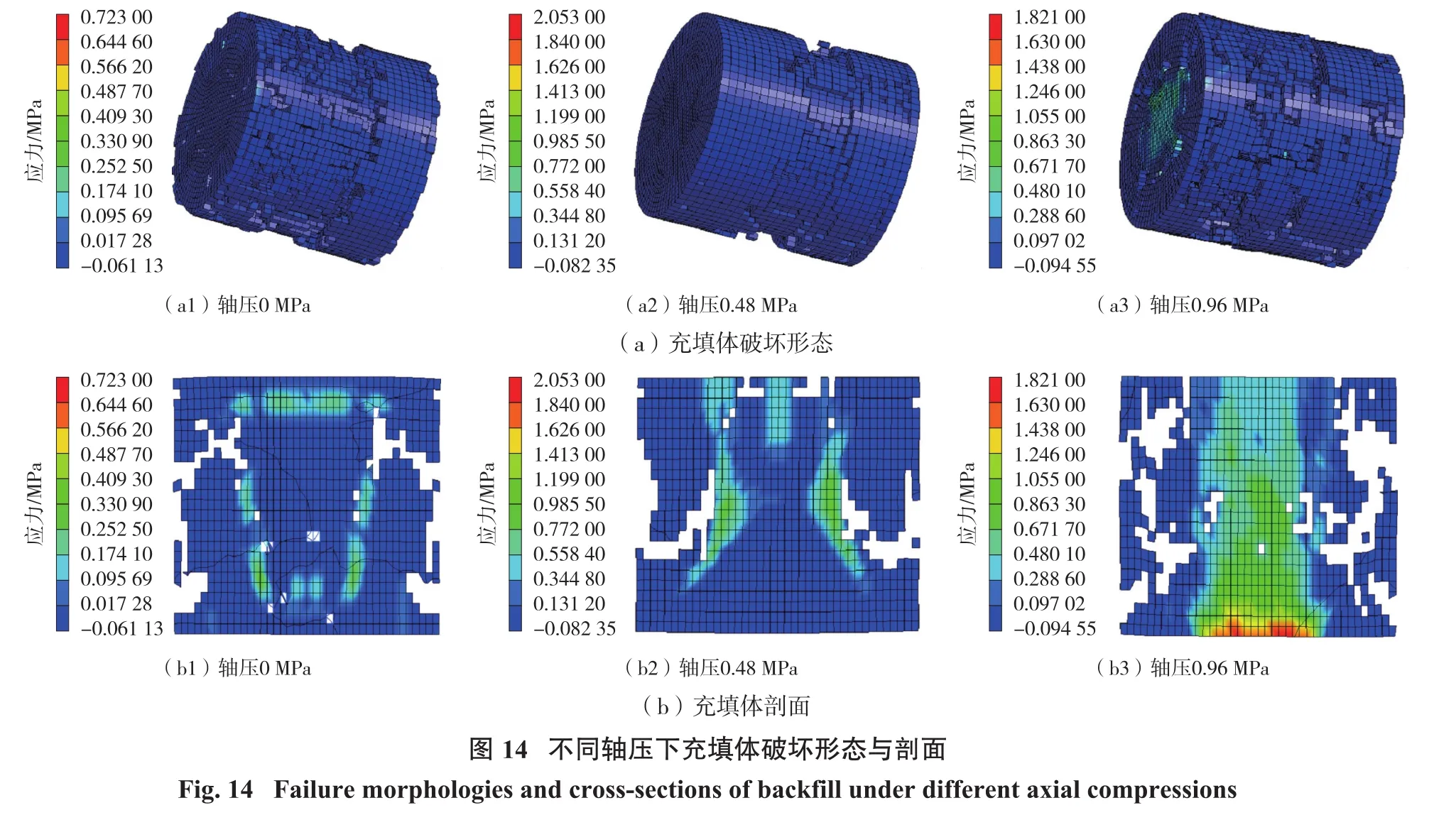
图14为t=0.004 5 s，v=5 m/s时，不同轴压下充填体破坏形态与剖面图。由图14可知：无轴压时为纵向劈裂横向拉伸所致破坏，靠近入射杆端部破碎较剧烈，施加轴压时为剪切破坏。轴压为0.48 MPa处试件破碎形态最为完整，且出现“X”型大块，当轴压增大到0.96 MPa，内部形成的潜在剪切破裂面进一步加剧，最终产生小圆台，对比不同轴压下的剖面图，进一步证实了上文论断。

图15为轴压0.48 MPa，v=5 m/s时，相同轴压作用下0°耦合体破碎过程与剖面图。由该图分析可知：整体破碎形态与物理试验具有较高吻合度。当t=0.002 57 s时，充填体表皮基本无破坏，内部由于轴压作用出现潜在剪切破裂面，t=0.002 58 s时，内部呈现出“X”型趋势，表皮开始脱落，随着应力波进一步传递，剪切面继续扩展、贯通，最终在t=0.002 59 s时，形成圆锥形小圆台，表皮破裂严重，但此时仍具有部分承载能力，与试验结果相似。

3.4 冲击应力波传递衰减分析

充填体中冲击波应力—时程曲线如图16所示。分析该图可知：该曲线测点取自靠近入射杆端部的48056节点和靠近透射杆尾部的54161节点。试件端部和尾部应力峰值分别为2.4 MPa、1.9 MPa，应力波衰减量为20%左右，这就可以解释图9及图10中靠近冲击波的试件前端比尾端更为破碎的原因，一方面源于冲击波的密实作用；另一方面则是充填体对应力波的传递具备一定阻碍作用，使得到达试件尾部的应力波峰值大大减小。

不同传递路径下充填体中冲击波的应力—时程曲线如图17所示。保持其它条件一致，取纯充填体和耦合体靠近透射杆处同一位置的节点，并测出其冲击应力波衰减时程图，可见冲击波经不同介质传递至充填体同一位置时，最大峰值应力出现时刻基本相同，但应力大小存在差异，冲击波经充填体传递到测点处的峰值应力为1.9 MPa，经花岗岩传递至测点处的峰值应力为1.7 MPa，经花岗岩传递后应力波衰减量比经充填体传递至测点时高9%左右，这主要是由于充填体和花岗岩对应力波阻碍能力不同引起的。

波阻抗是表征波在材料中应力波反射及穿透能力的常用指标，大小等于材料的密度与纵波波速的乘积。由于导杆波阻抗值远高于试件，因此，一般假定相同入射速度下冲击波经入射杆传递到不同试件时的波速基本相同，花岗岩密度比充填体大，故其波阻抗值高于充填体。因此，冲击波经岩石传递到同一节点处的峰值应力小于经充填体传递到同一节点的峰值应力，且耦合体中冲击应力波的衰减速度远高于充填体试件中的冲击应力波。

4 结 论

（1）动静组合加载下保持轴压一定，充填体动态抗压强度与应变率相关性显著，随着应变率增大而增大。在相近应变率下增大轴压梯度，充填体动态抗压强度呈现出先增大后减小趋势，轴压为静载强度40%时达到最大动态抗压强度。

（2）动静组合加载下充填体应力—应变曲线主要分为弹性阶段、屈服阶段及破坏阶段，无明显密实阶段，随着所施轴压的增大，充填体试件弹性模量呈现先增大后减小趋势。

（3）常规SHPB冲击下充填体破坏模式为劈裂拉伸破坏，动静组合加载下充填体破坏模式为剪切破坏，轴压作用下会产生具有一定承载能力的“X”形大块及圆锥形小圆台。冲击波经不同传递路径或不同角度传递至充填体时，破坏模式本质上仍为剪切破坏。

（4）应用ANSYS/LS-DYNA模拟充填体及耦合体在动静组合加载下的冲击过程，所得应力—应变曲线、破坏形态等特征与物理试验结果高度吻合。冲击波经不同传递路径至充填体时，最大应力峰值出现时刻基本相同，应力大小差异较大，经岩石间接作用于充填体的应力波衰减量及衰减速度较冲击波直接作用于充填体时要大。