嗣后充填采场爆破与充填体稳定协同效应研究

张 金 金爱兵 陈帅军

（1.山东金鼎矿业有限责任公司，山东淄博255000；2.北京科技大学土木与资源工程学院，北京100083；3.北京科技大学金属矿山高效开采与安全教育部重点实验室，北京100083）

充填体在爆破载荷作用下的破坏是一个极其复杂的过程，嗣后充填二步采爆破设计中，保证爆破效果的同时，还要兼顾充填体稳定［1］。岩石受爆破冲击载荷的作用，应变率约在10～103s-1范围内［2］，众多学者研究表明［3-6］：岩石材料的动力学特性与静力学特性有很大区别，传统准静态试验已经不能满足岩石动荷载作用的研究需求。因此，通过动荷载试验获得矿岩动力学参数是采场爆破效果研究的前提和基础。

分离式霍普金森压杆（Split Hopkinson Pressure Bar，SHPB）试验是研究高应变率下材料力学特性的有效手段之一［7-8］。李占金等［9］利用分离式SHPB试验装置对磁铁矿试件开展了不同应变率下的冲击试验，试验结果表明：磁铁矿石的动态强度和动态弹性模量均表现出较强的应变率效应。宋小林等［10］用SHPB对大理岩巴西圆盘和平台巴西圆盘进行了动态劈裂试验，指出在试件中心贴应变片的方法可以较便捷地获得大理岩等脆性材料的动态抗拉强度。赵毅鑫等［11］结合SHPB和数字图像相关（Digital Image Correlation，DIC）技术对煤样的动态抗拉强度进行了研究，指出煤样的动态抗拉强度与冲击速度和层理倾角相关。张文清等［12］对不同煤样的动态抗压特性进行了研究，得出煤的动态抗拉强度和峰值应变均有应变率强化特性。上述研究成果充分证明，利用SHPB试验装置可以获得岩石材料的动态参数。

随着计算机技术的发展及动力数值方法不断成熟，爆炸问题的数值仿真分析在爆炸力学研究中发挥的作用日益重要［13］。岩石爆破数值模拟研究始于20世纪四五十年代，LS-DYNA、ABAQUS和AUTODYNA等通用非线性动力学软件的推出和广泛使用，使得岩石爆破的数值模拟研究达到了一个新的高度［14］。DUC-KIEN等［15］利用LS-DYNA软件研究了不同截面尺寸钢筋混凝土在爆破后的损伤情况，试验结果表明：随着高径比增大，石块整体损伤情况增多，同时起爆点在中部的损伤情况比在底部严重。YI等［16］利用LS-DYNA软件对分段崩落法矿山生产爆破的扇形炮孔延时起爆时间和起爆位置进行了研究，结果表明：适当提高起爆时间可以提高矿岩的破碎效果。邓红卫等［17］利用LS-DYNA2D软件对梅山铁矿扇形中心孔起爆段别进行了优化，减少了采区附近的爆破振动。尹丽冰［18］结合MATLAB和ANSYS/LS-DYNA软件就某铀矿生产爆破对地表的振动强度进行了研究，认为按7 ms/m的微差间隔选取雷管段别的减振效果最明显。费鸿禄等［19］针对硬岩巷道掘进爆破效率低的问题，利用LS-DYNA软件对多种掏槽方式进行了模拟，通过分析模拟结果并结合现场试验，认为复式筒形装药结构方案最优。以上成果均是利用ANSYS/LS-DYNA软件研究孔网参数，优化爆破效果，但是对嗣后充填采矿法二步采爆破效果及充填体稳定性的研究涉及较少，因此有必要开展爆破效果与充填体稳定性协同效应方面的研究。

在嗣后充填矿山采矿工作中，爆破参数优化不仅需要考虑爆破效果，还应该充分考虑到爆破过程对一步骤充填采场稳定性的影响。本研究通过分离式霍普金森杆试验获得矿石和充填体的动力学参数，并据此进行不同孔底距、排距及充填体保护层厚度的数值模拟，结合现场监测，对嗣后充填二步采场爆破作用及充填体稳定性协同效应进行研究，以获得兼顾爆破效果和充填体稳定性的最优爆破孔网参数。研究成果可对该类矿山二步采过程中采场爆破孔网参数设计和充填体稳定性分析提供借鉴。

1 矿石和充填体动态力学特性试验

准确获得矿石和充填体的动态力学参数是进行数值模拟研究的基础，本研究通过矿石动态SHPB试验获得其动态抗压强度和动态抗拉强度，并通过充填体的动态抗压试验获得其动态抗压强度（充填体与矿石接触，并未与炸药直接接触，充填体破坏属于动态受压破坏，因此，本研究主要分析充填体动态抗压强度），为后续数值模拟及现场监测提供数据支持。

1.1 SHPB系统

动态力学试验采用的SHPB装置主要由压杆系统、数据采集系统、测量系统和控制系统组成。压杆系统包括撞击杆、入射杆、透射杆和吸收杆，测量系统包括入射杆和透射杆上的传感器测量系统和撞击杆的子弹速度测量系统，试验装置如图1所示。

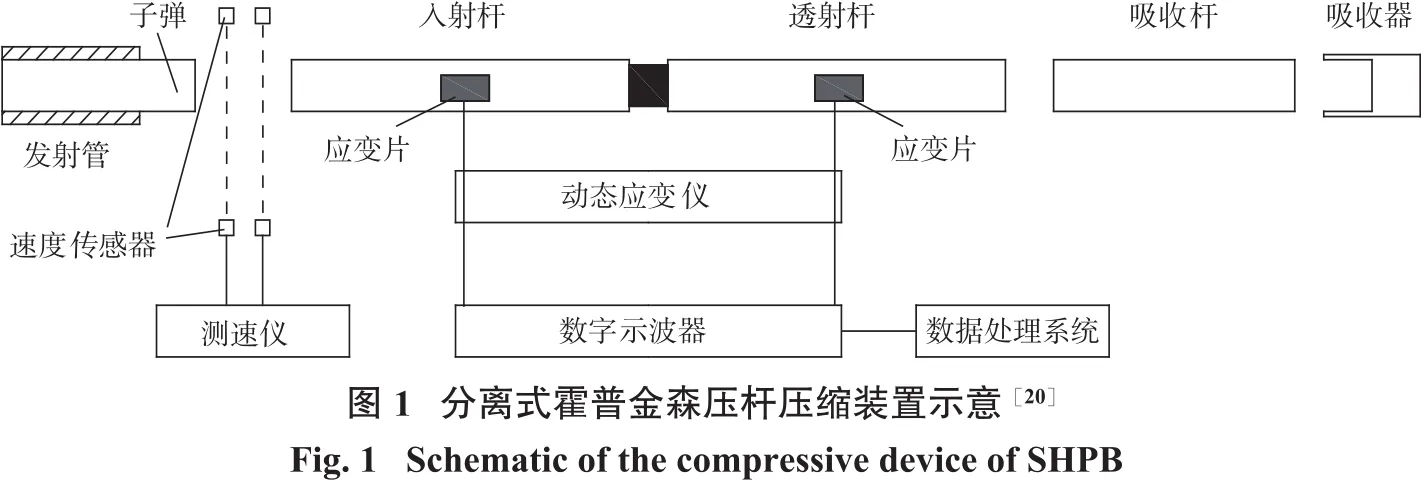
分离式霍普金森试验装置基于一维应力波假定和均匀性假定［8］，利用子弹撞击入射杆，一维冲击波因入射杆和试件的波阻抗不同分离成反射波和透射波，反射波在入射杆和岩石试件的端面来回反射与透射直至应力平衡，利用传感器测量系统获取的脉冲波应力时间历程曲线推导试件的应力—应变关系曲线。

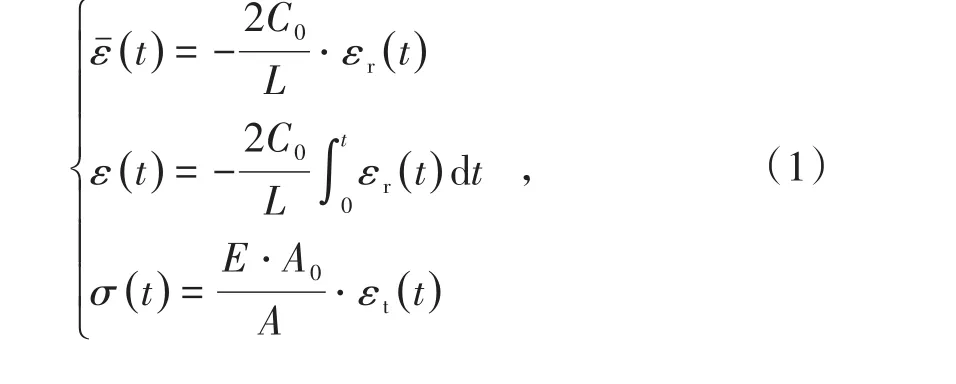
式中：C0为压杆的弹性波波速，m/s；E为压杆的弹性模量，MPa；A0为压杆的横截面积，m2；A为试件的横截面积，m2；L为试件长度，m；εr(t)、εt(t)分别为反射波和入射波信号；t为反射波和入射波的传播时间，s。

1.2 动态压缩试验

1.2.1 铁矿石动态压缩试验

金鼎铁矿采用阶段空场嗣后充填采矿法，矿石品位30%～70%，平均品位49.5%，本研究取50.3%品位的磁铁矿试样进行加载，获得了磁铁矿的动态压缩应力时程曲线和动态应力—应变曲线，分别见图2和图3。

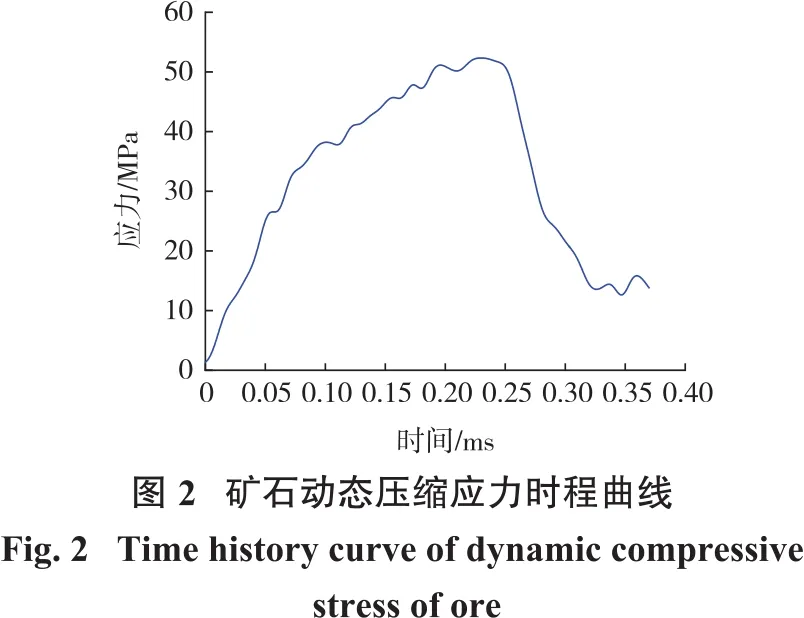
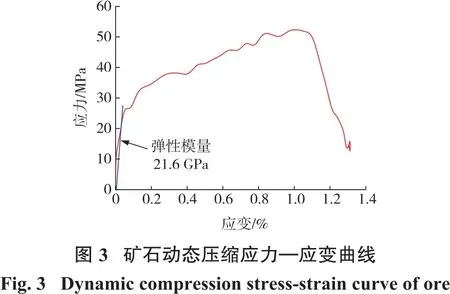
由图2、图3可知：在冲击气压一定的前提下，试件的破坏时间在0.1 ms左右。50.3%品位的磁铁矿试样峰值应力为53.8 MPa，对应的动态弹性模量为21.6 GPa。

1.2.2 充填体动态压缩试验

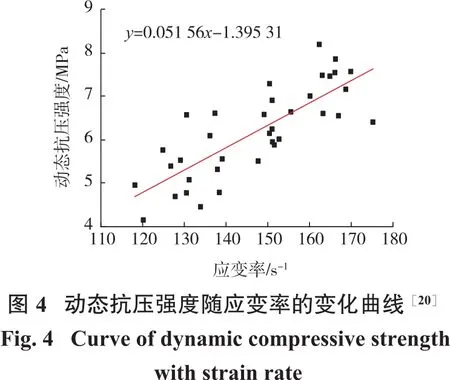
充填体试样料砂比为1∶4，浓度为54%，恒温恒湿养护28 d，根据前期对该配比和浓度充填体试样的试验研究成果［20］，充填体静态抗压强度为3.4 MPa，充填体动态抗压强度与应变率的关系如图4所示。由图4可知：充填体试样的动态抗压强度均大于其静态抗压强度，且充填体试样的动态抗压强度随着应变率增大呈线性增大关系，试验中充填体的平均动态抗压强度为6.19 MPa。

1.3 铁矿石动态劈裂试验

由于岩石属于脆性材料，其抗拉强度和变形极限都很小，在爆破作用下，其破坏形式主要表现为拉伸破坏。因此，本研究选用与第1.2.1节相同的磁铁矿加工成直径50 mm、高度25 mm的标准圆盘试件，试验示意图如图5所示。利用二波法可获得拉应力σt：

式中：P1为入射波；P2为反射波；D为试件直径；H为试件高度。

图6为50.3%品位的磁铁矿试样动态拉伸的应力—时程曲线。由图6可知：在冲击气压一定时，铁矿石破坏时间在0.1 ms左右；50.3%品位的磁铁矿试样的峰值应力为11.73 MPa。

2 数值模拟

以山东金鼎铁矿嗣后充填二步采场为工程背景，采用有限元软件ANSYS/LS-DYNA对采场爆破效应及充填体响应进行模拟分析。

2.1 材料参数及本构关系

材料采用弹塑性材料（*MAT_PLASTIC_KINEMATIC），采用SHPB试验中铁矿石和充填体试样的测试数据作为模拟参数（表1）。

炸药采用高性能炸药材料*MAT_HIGH_EXPLOSIVE_BURN和JWL状态方程描述［22-26］，爆轰产物采用JWL状态方程进行压力计算：

式中，p为爆轰气体产物爆炸的压力，Pa；ω为格林艾森参数，即在体积一定时，压力相对于内能的变化率；A、B、R1、R2为试验确定的常数；E0为初始内能密度，J/m3；V为爆轰产物的相对体积。

矿山生产爆破过程中选用2#岩石乳化炸药，参考文献［27］，2#岩石乳化炸药JWL状态方程参数取值见表2。

空气可采用*MAT_NULL材料模型代替，状态方程可用线性多项式描述：

参考文献［28］，空气及状态方程参数取值见表3。

2.2 模型构建及模拟方案

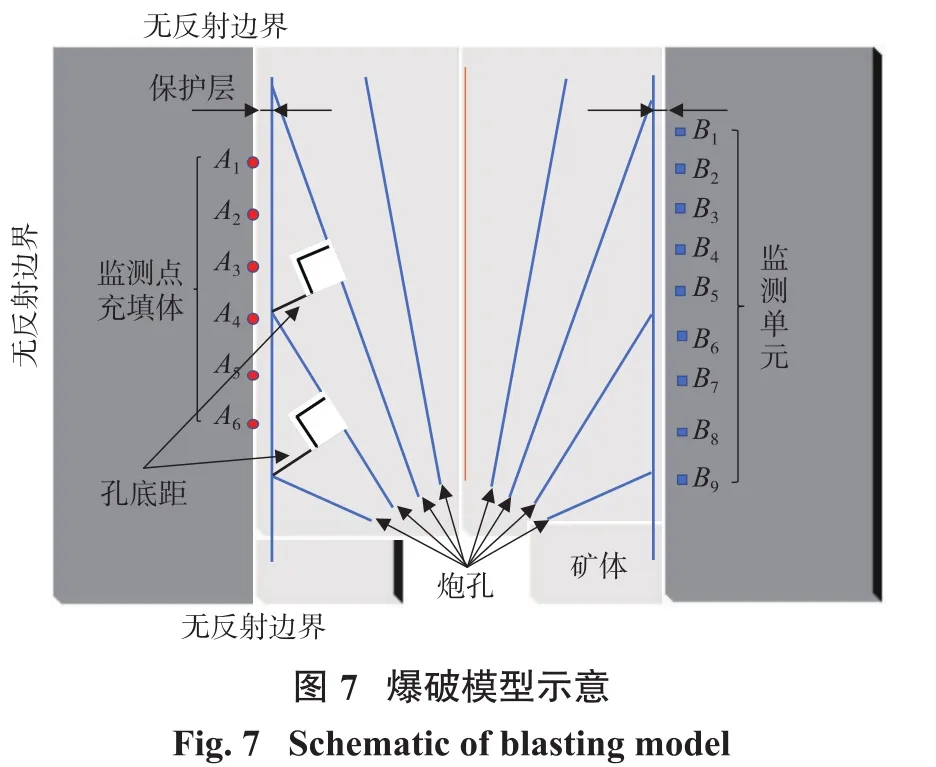
金鼎铁矿采用阶段空场嗣后充填采矿法，上向扇形孔爆破落矿，孔底距3.5 m，排间距2.0 m。在实际爆破生产中，存在块度不均匀、大块率高且充填体局部垮塌的问题，因此，有必要对采场的不同爆破孔网参数进行研究，以获得更好的爆破效果，同时控制爆破振动对充填体的影响。在ANSYS/LS-DYNA前处理软件中进行建模，考虑到模型的对称性，缩短计算时间，取1/4模型进行计算，在ANSYS/LS-DYNA软件中进行镜像处理。模型中宽度和高度均为20 m，厚度为2.2 m。为进行数值模拟，假设矿体为均值弹塑性体，采用的单位为cm-g-μs，为消除边界影响，除了自由面外，对称边界设置对称约束条件，其余边界均为无反射边界，无反射边界不造成应力波反射。本研究构建的爆破模型如图7所示，炮孔模型及网格划分如图8所示。结合现场工程实际和前期研究成果［20］，本次数值模拟方案如表4所示。

2.3 数值模拟结果分析

2.3.1 不同孔底距爆破效果分析

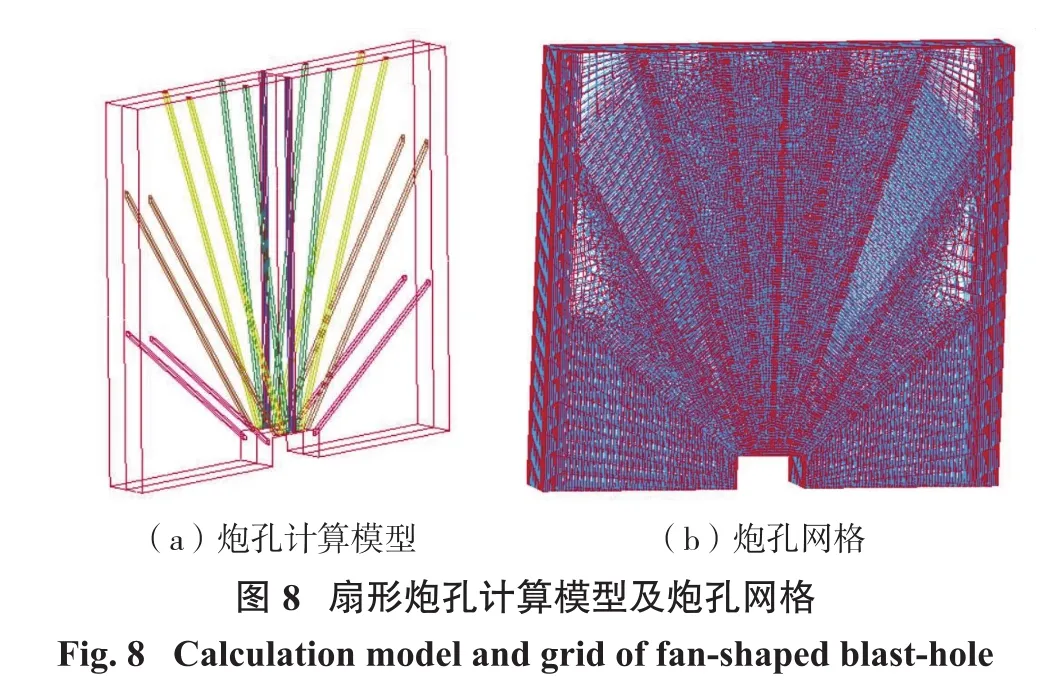
以孔底距为变量，分析5种孔底距应力波传播情况。图9为各方案爆破末期的应力波等值面图，此时应力波已经覆盖整个模型，炸药的能量已经达到最大。孔底距从2.7 m增大至3.5 m，应力波等值面范围先扩大后缩小，高应力区范围先增多后减小，均在孔底距为3.1 m时达到最大，说明该方案能量利用率较高，爆破效果较好。

为了定量比较各方案的有效应力，在中心炮孔与右侧相邻炮孔轴线上选择两个特定单元进行进一步分析，特定单元位置如图10所示，监测单元分别记为D1和D2。为减小误差，取两个单元最大有效应力的平均值进行比较，按此方法获得5组采集数据见图11。

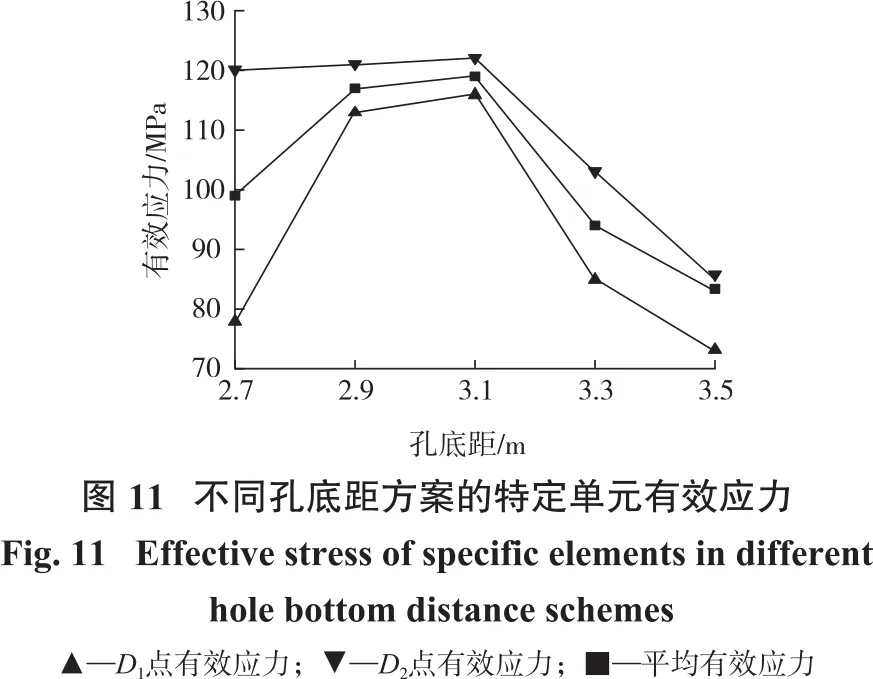
由图11可知：D1和D2两点单元有效应力及平均有效应力均是先增加后减小，均在孔底距3.1 m方案处达到最大值。孔底距2.9 m和3.1 m方案处D1和D2两点单元有效应力及平均有效应力相差很小，但与其他方案的差距较大，说明孔底距2.9 m和3.1 m方案的炸药能量得到较好的利用，能够传递更大的应力波，从而可以更好地破碎矿石。

2.3.2 不同排间距爆破效果分析

以排间距为变量，分析2种排间距方案的应力波传播情况，如图12所示。爆破末期应力波已经覆盖整个模型，排间距2.0 m时应力波未传播到孔口，容易在孔口形成大块，而排间距1.8 m方案的应力波能够传播到孔口，同时排间距为1.8 m的模型代表中高应力区更多，矿石在冲击载荷的作用下更容易破碎，获得更好的爆破效果。

与2.3.1节类似，同样在两个方案中各选择两个特定单元（图13），记为F1和F2。两个方案特定单元的最大有效应力和应力平均值见图14。由图14可知：排间距1.8 m方案的A、B两点最大有效应力及应力平均值均大于排间距2.0 m方案。说明排间距1.8 m方案可以获得更大的应力，排间距2.0 m方案更容易产生大块。因此排间距为1.8 m的爆破方案更优。

2.3.3 不同保护层厚度充填体的爆破响应

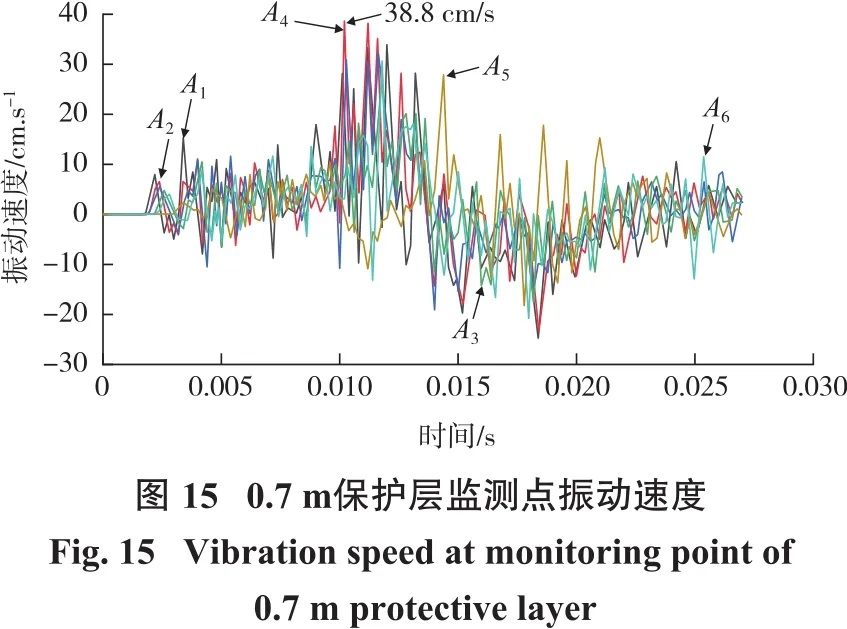
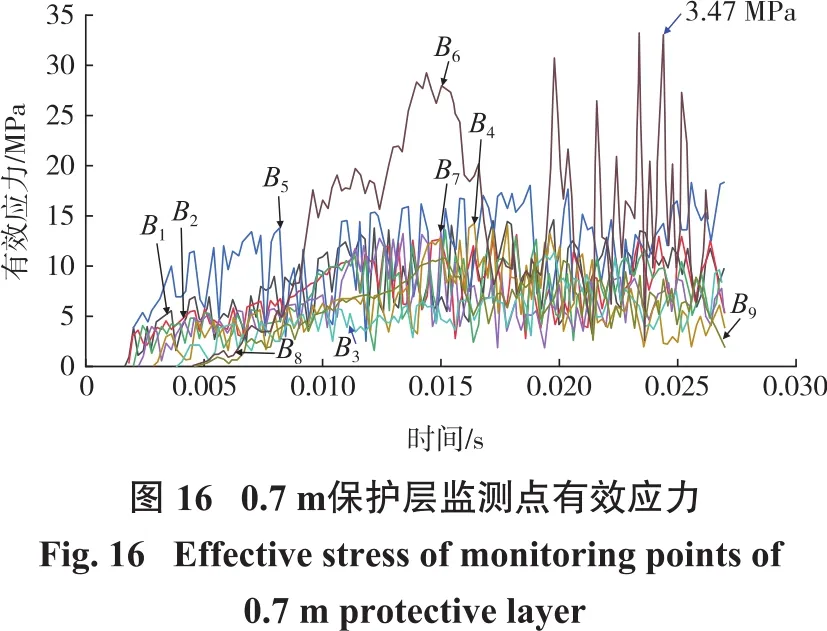
以保护层厚度为变量，在矿体和充填体之间均匀布置监测点，质点振动速度监测点位置如图7（A1、A2、A3、A4、A5和A6点）所示，有效应力监测单元位置如图 7（B1、B2、B3、B4、B5、B6、B7、B8和 B9点）所示（模型左右对称，故将有效应力监测单元在模型右侧表示）。保护层厚度为0.7 m时，监测点振动速度—时间曲线和监测单元有效应力—时间曲线如图15和图16所示，充填体最大振动速度为38.8 cm/s，最大有效应力为3.47 MPa。

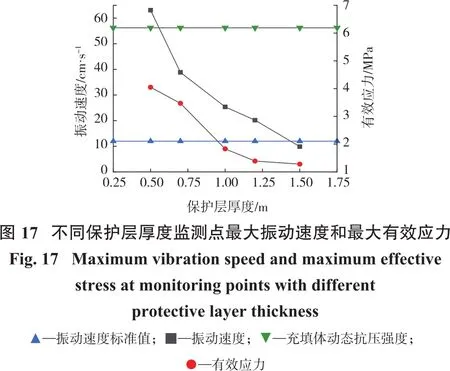
进一步处理数据得到振动速度和有效应力随保护层厚度的变化曲线，如图17所示。由图17可知：随着保护层厚度增大，矿体和充填体之间的振动速度和有效应力均减小，说明增大保护层厚度可以有效保护充填体稳定性。依据《爆破安全规程》（GB 6722—2014）［25］要求，充填体质点振动速度应小于12 cm/s，因此保护层厚度应大于等于1.5 m才能保证充填体稳定。同时充填体SHPB试验结果显示，充填体的动态抗压强度为6.19 MPa，而监测单元的有效应力均小于6.19 MPa。综合振动速度和有效应力两个因素，保护层厚度不小于1.5 m能保证充填体稳定。

综合以上不同孔网参数方案的数值模拟结果可知，孔底距2.9～3.1 m、排间距1.8 m、保护层厚度不小于1.5 m的爆破方案应力波传播范围较广，炸药能量利用更充分，可以获得较好的爆破效果且能保证充填体稳定。

3 现场爆破监测及充填体质点振动检验

模拟结果显示，采用2.9～3.1 m孔底距、1.8 m排间距以及1.5 m以上保护层厚度能够满足爆破效果和充填体保护要求。本研究采用现场监测手段对数值模拟结果进行验证，由于孔内应力难以监测，故通过监测质点振动速度加以验证。

3.1 质点振动速度监测

在现场爆破监测中，为了保证监测过程的安全，不直接监测爆破作用下的充填体质点振动速度，而是在采场与爆源一定距离处布置监测点，获得测点数据，通过回归分析获得振动速度与距离的规律公式，从而推算充填体质点振动速度。

质点峰值振动速度采用TC-4850型爆破振速仪测量，爆破振速仪由数据采集主机和三轴向振动速度传感器组成，如图18所示。选择金鼎铁矿-410 m水平3403区为振速监测矿房，为保护实验装置，在距离爆源中心25 m处每隔2～3 m布置4个测点，分别为1#、2#、3#和4#监测点，具体位置见图19。

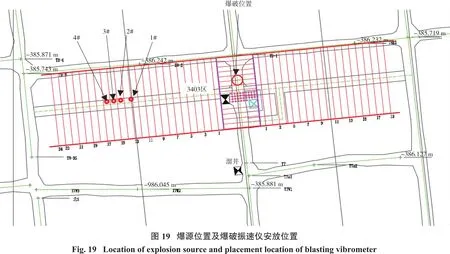
在3403区进行爆破后，爆破振速仪监测到4个测点X、Y、Z 3个方向的振动速度数据，将数据导入爆破振速仪配套的后处理软件Blasting Vibration Analysis（BVA）中得到3个方向的振动速度波形图，其中X方向与矿房走向垂直，Y方向与矿房走向平行，Z方向为矿房高度方向。由于此次试验是监测爆破振动速度对充填体的影响，故选择与矿房走向垂直的X方向的振动速度进行分析，4个测点的最大振动速度见表5。

3.2 数值模拟有效性检验

3.2.1 现场监测结果

本研究以《爆破安全规程》（GB 6722—2014）［29］建议的萨道夫斯基公式为基础，采用最小二乘法［30-31］对爆破现场试验数据进行拟合，获得萨道夫斯基公式（式7）的相关参数：

利用测点数据进行萨道夫斯基回归分析，采用相关系数R对K、α回归系数进行显著性检验。对给定的显著性水平α，当|R|＞P（αPα为常数，可通过查相关系数临界值表取得）时，线性相关；否则，线性不相关。取显著性水平α=0.05，通过查相关系数临界值表，可得Pα=0.80。将表5中的数据拟合回归计算得K=8.71，α=1.49，样本的相关系数R=0.962，大于 0.80，线性关系非常明显，因此X方向的萨道夫斯基公式为

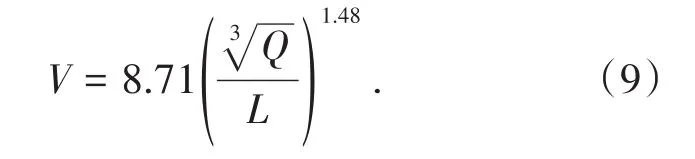
采场中充填体到爆源的距离L=10 m，生产爆破的装药量Q=400 kg，代入萨道夫斯基公式（式（9））计算得V=5.542 cm/s。

3.2.2 数值模拟结果

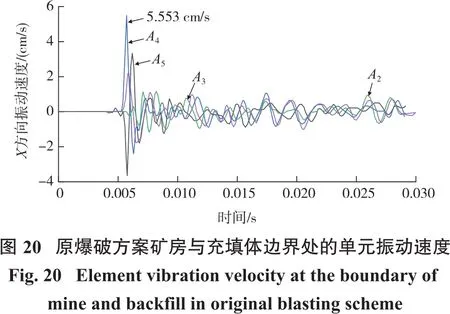
在ANSYS/LS-DYNA软件中建立原爆破方案数值模型，其中孔底距3.5 m、排间距2.0 m、保护层厚度1.5 m，在矿房与充填体交界面选择4个监测点（图7中A2、A3、A4、A5点），获得质点振动速度，结果如图20所示。由图20可得最大爆破振速为5.553 cm/s，与萨道夫斯基公式得到的结果基本一致，说明利用ANSYS/LS-DYNA软件进行爆破效应和充填体稳定性协同效应的数值模拟研究具有可行性。

4 结 论

采用分离式霍普金森实验装置获得了铁矿石和充填体的动态力学参数，在此基础上利用有限元软件ANSYS/LS-DYNA研究了嗣后充填采场爆破与充填体稳定性的协同效应，并结合现场爆破振动监测结果，分析了数值模拟结果的可靠性，得出以下结论：

（1）50.3%品位的磁铁矿动态抗压强度为53.8 MPa，动态弹性模量为21.6 GPa、动态抗拉强度为11.7 MPa，充填体平均动态抗压强度约为6.19 MPa，试验数据可用于判断充填体稳定性。

（2）考虑到充填采场爆破与充填体稳定性的协同效应，采用孔底距2.9～3.1 m、排间距1.8 m、保护层厚度大于等于1.5 m的孔网参数，能够使炸药的能量充分利用，获得更好的爆破效果；同时充填体质点振动速度和有效应力在安全范围内，可以保证充填体稳定。