弹载组合导航算法仿真实现

陈 耿 于 山 方楚雄 吴安安 冯治娇

(西安比特联创科技有限公司 西安 710100)

0 引言

弹道修正弹是在20世纪80年代中期发展起来的新型弹药，其基本概念是：能够在弹丸飞行过程中实时测量弹载体姿态和位置信息，通过控制系统实现弹道修正、减小弹道偏差、提高打击精度的弹药。

1 工作原理

目前国内主流弹体工作过程见图1所示。

图1 弹体工作过程图

目前全姿态测量是弹道修正的关键技术之一，其测量传感器主要受限于：弹丸发射过载大(普遍大于10000g)，滚转角速度大(一般大于3600°/s)，弹体空间体积小，以及需要低成本。

基于以上几点，传统高精度的光纤陀螺和激光陀螺由于体积大成本高的特点无法直接应用于弹道修正弹。所以目前主流实现方案为MEMS技术的惯性器件组成的惯性测量单元加上卫星导航系统实现完整的惯性/GPS组合导航系统。

2 试验过程概述

用已有的实弹数据，包含惯性测量单元(以下简称IMU)以及卫星导航系统(以下简称卫导)数据进行实时仿真，对仿真结果进行分析。具体试验环境搭建情况参见图2所示 。

图2 试验环境搭建

算法实现过程简要框图见图3所示 。

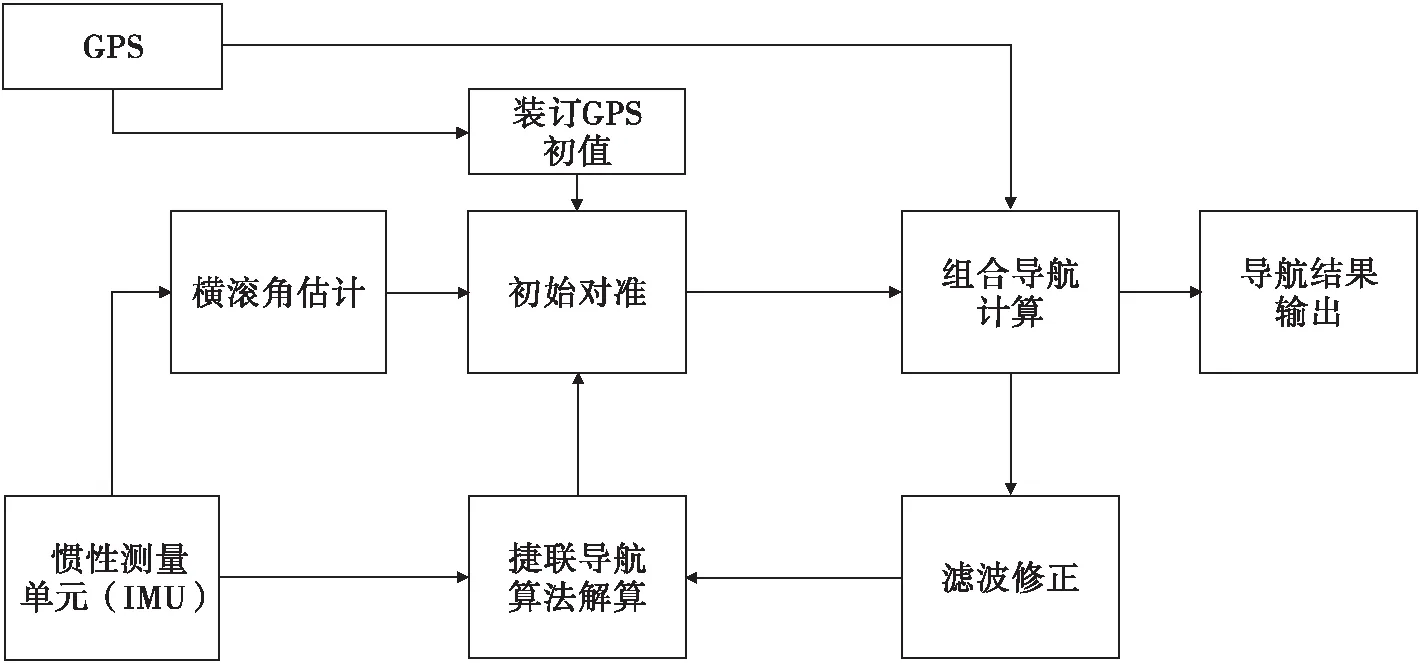
图3 算法实现过程简要框图

3 算法实现

本次算法设计实现了滚转角高转速条件下动态对准技术和航姿位置解算功能，算法仿真设计主要使用非线性系统的卡尔曼滤波器(扩展卡尔曼滤波器，Extended Kalman filter-EKF)[2]实现。

假设连续或离散的随机系统由非线性离散方程式和记录测量的模型方程式表示(见表1所示)。

表1 非线性离散方程式和记录测量的模型方程式

所采用的线性化方法要求函数f和h连续两次微分。

用符号δ标出被估计航迹的小增量为

δxk=xk-xk(-)

(1)

(2)

xk(-)=xk|k-1——系统状态外推 (预测)

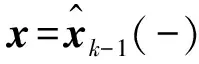
(3)

由此，得出

(4)

则

(5)

(6)

(7)

(8)

算法中状态矢量包涵姿态四元数Λ和х轴角速度传感器的零偏β。状态矢量方程可写成式(9)

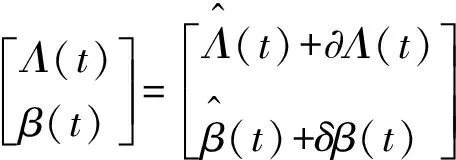
(9)

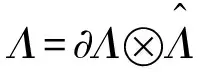
(10)

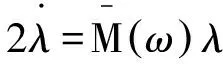
(11)

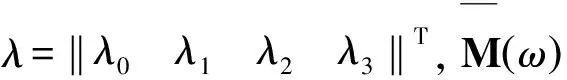
(12)

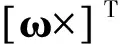
(13)

由此，可写出

(14)

零偏的不确定性是使用陀螺传感器的主要问题。当陀螺零偏存在误差时对姿态定位会带来很大影响，同时陀螺零偏值随温度也有变化。因此在与其他传感器组合使用陀螺传感器时，使用以下方法确定零偏值。

使用陀螺传感器零偏测量模型[4]为

(15)

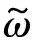
ηv和ηu为根据E[ηv]=0和E[ηu]=0的角速度和零偏测量速度白噪声。

现假设陀螺误差量测模型中，陀螺零偏为固定值δβ=0；现在将以上所有描述的写为

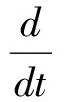
(16)

状态线性化转换矩阵(雅科比矩阵)[3]为式(17)。

(17)

从连续形式转换成离散形式时，由于计算步骤中矩阵F不变，可将转换矩阵写成式(18)。

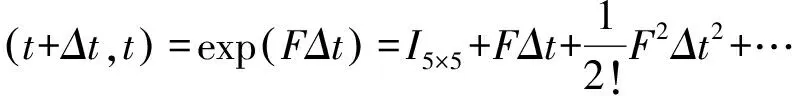
(18)

为节省计算资源，实现时只取两个一次分解项。

4 仿真结果分析

将实弹IMU数据及卫导数据按时序发送至仿真系统后，仿真结果如下，其中根据弹载体卫星导航系统数据可以得出以下弹体飞行路径[5]，见图4所示。

图4 弹载体飞行路径

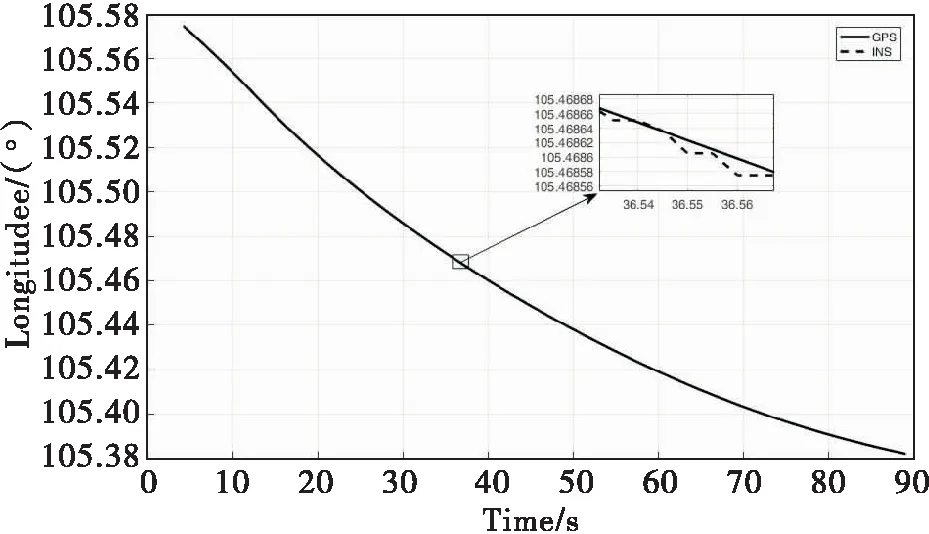
图5 经度方向组合导航位置精度

图6 纬度方向组合导航位置精度

图7 高度方向组合导航位置精度

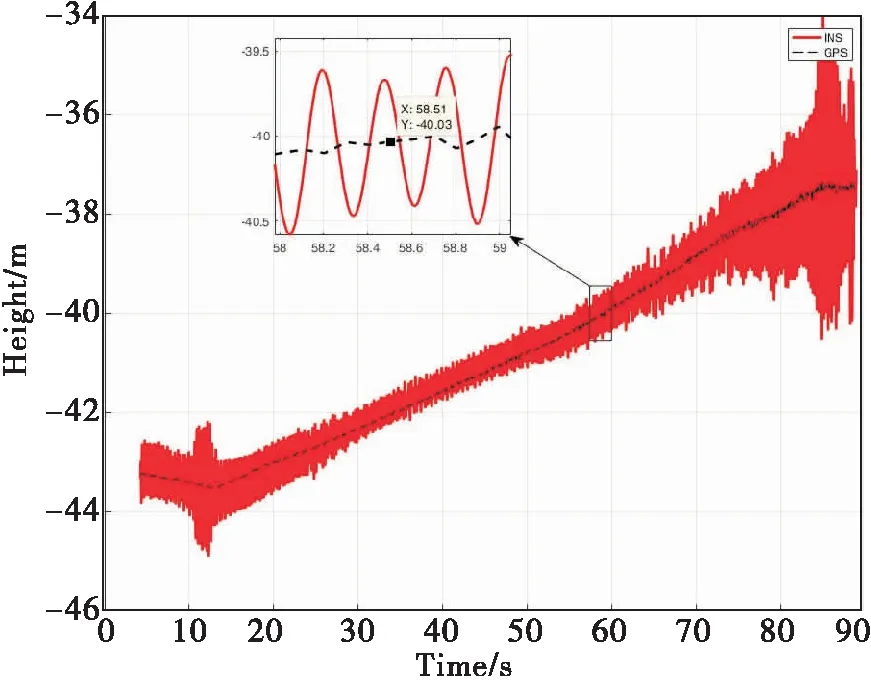
图8 组合导航方位角精度

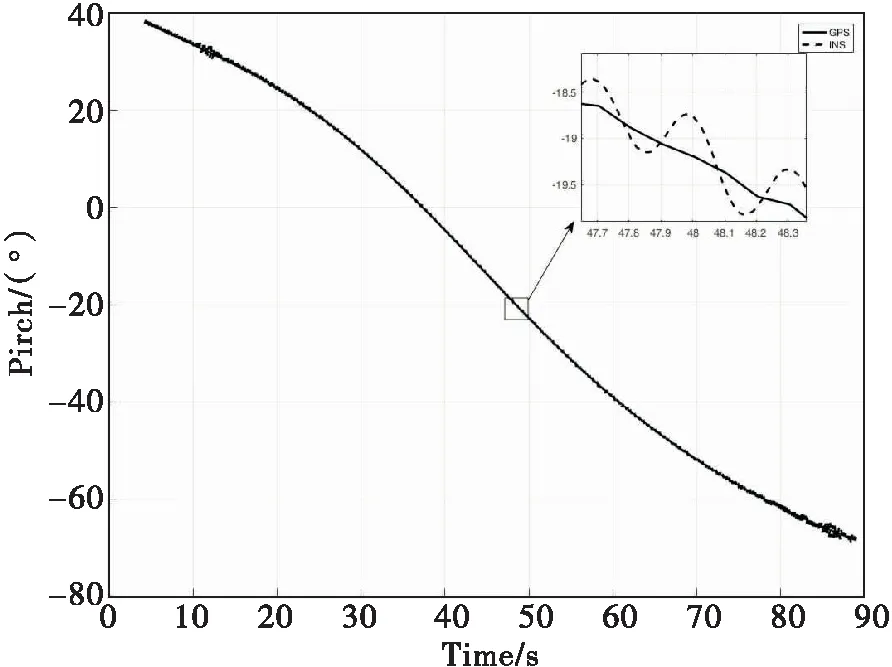
图9 组合导航俯仰角精度

图10 组合导航横滚角精度(节选)

通过以上数据分析，其中位置精度、方位角以及俯仰角精度均可用卫导信息相互验证，横滚角无法通过卫导信息验证，目前采用反证法进行了论证，通过多次递归方式进行计算，其最终结果均能相互吻合。

试验中也考虑卫导信息中断情况下的精度分析，具体结果参见表2和表3所示。根据以上内容可以得出以下结论：

表2 导航位置精度及速度精度计算(ΔB为经度方向误差，ΔL为纬度方向误差，ΔH为高度方向误差，ΔVe为东向速度误差，ΔVn为北向速度误差，ΔVu为天向速度误差)

表3 导航姿态精度计算(ΔΦ为方位角误差，Δθ为俯仰角误差，Δγ为横滚角误差)

1)根据以上算法计算结果满足现有弹体载体的导航要求，证明了算法理论行之有效；

2)通过现有的弹体数据验证了该算法正确有效；

3)该算法适用于实时弹载导航系统。

5 结束语

根据以上推导过程及数据分析，该解算算法具有以下优点：

1)递归性(可更好的应用于实时模式)；

2)横滚轴角速度传感器系统误差估计；

3)可以有效解算精度较高的姿态精度和位置精度。

本文论证了以非线性(扩展)卡尔曼滤波器EKF为基础研发的解算角度姿态参数的连续递归算法；并且以实弹测试数据为基础进行了仿真，仿真结果较好，并且经论证可以满足后续控制精度，后续我们将继续开展实弹验证工作。