SMA鼓包迟滞建模与控制策略
陈旭亮,张琛,季宏丽,裘进浩
南京航空航天大学 航空学院 机械结构力学及控制国家重点实验室,南京 210016
激波控制鼓包(Shock Control Bump,SCB)是一种流动控制技术,能够明显减小激波阻力,其具有结构简单、不需要大改翼型结构、不附带黏性阻力等优点[1-3]。李沛峰等[4]通过CFD计算,研究了鼓包高度、位置和长度对减小激波阻力的影响。固定挠度激波控制鼓包在设计点附近具有较好的减阻效果,但在远离设计工况时,却会破坏原有的翼型结构,带来很大的负面作用,导致飞行器阻力急剧增大。为了解决这一问题,帝国理工的Jinks等[5]提出了自适应鼓包的概念,设计了一种单点驱动的铝制鼓包结构,并对其结构设计,驱动等进行了优化研究,研究结果表明自适应鼓包在较大飞行包络能够有效降低激波阻力。然而,铝制鼓包为传统机械结构,驱动方式复杂,一体性较差。
形状记忆合金(Shape Memory Alloy,SMA)是一种常见的智能材料,其具有独特的形状记忆效应,可以自感知温度变化,将热能转化为机械能,对外输出力或位移,但与其他智能材料如压电材料相比,其响应速度较慢[6-8]。飞行器处于巡航状态时鼓包外形不需要发生频繁改变,故可适当降低对响应速度的要求。聂瑞等[9]提出了一种基于形状记忆合金的自适应鼓包实现方式,对SMA鼓包进行了仿真研究,在温度升高时,鼓包挠度变大,降温时挠度变小,最大挠度变化可达鼓包长度的4%。然而在飞行器巡航状态下,环境温度往往可达-50 ℃,加热使鼓包挠度变大需要较多的能量且不易实现,所以训练一种降温挠度变大,升温挠度减小的SMA鼓包更符合实际要求。在对形状记忆合金进行驱动控制时存在温度/位移迟滞现象。迟滞现象往往会降低系统的控制精度,从而给SMA鼓包的精确控制带来极大挑战。描述迟滞现象的常见模型有Preisach模型[10]、PI(Prandtl-Ishlinskii)模型[11]、KP(Krasnosel′skii-Pokrovskii)模型[12]、Duhem模型[13]与神经网络模型等。Preisach模型提出时间较早,被广泛应用于不同迟滞系统,Nguyen和Ahn[14]基于Preisach模型完成了对SMA驱动器的迟滞特性辨识,并利用模糊规则求解迟滞逆模型来对SMA驱动器进行了前馈控制,Preisach模型的缺点是模型辨识难度较大,得到完整模型需要大量实验数据。PI模型由Preisach模型改进而来,PI模型存在解析逆,能够较为方便地得到迟滞逆模型,Feng等[15]使用广义PI模型对SMA微执行器进行迟滞补偿,并通过仿真验证了该方法的可行性。然而PI模型仅能描述对称的迟滞现象,SMA执行器在实际应用中表现出的迟滞现象往往是非对称的,故PI模型的应用场景受到了较大限制。Duhem模型是基于微分方程的迟滞模型,针对不同的控制对象需要选择不同的函数,Liu等[16]使用Duhem模型来描述SMA驱动器的未知迟滞现象。在进行函数选择时,同一个函数往往只能适用于某一模型,在对新模型进行建模时存在函数选择困难的问题。Mai等[17]提出了一种自适应逆模型控制器,使用DNN(Deep Neural Networks)神经网络识别SMA驱动器电压/位移关系,神经网络在训练过程中较为依赖训练样本。KP模型同样是由Preisach模型改进而来,由于引入了极值记忆值,模型辨识难度降低。本文中的迟滞建模方法结合了KP模型与粒子群算法的优势,通过较少的实验数据得到了迟滞模型的动态特性,相较于传统的Preisach模型以及采用其他辨识方法来进行KP模型参数辨识的研究具有更好的便利性与可行性。
现有文献中研究的SMA驱动器常常为SMA丝,其只具备单向记忆效应,驱动器需要外加载荷才能使SMA丝复原,本文提出的SMA鼓包为板壳结构,其具有双向记忆效应,仅通过改变温度就能使其挠度变化。考虑到激波控制鼓包在最优设计点以外一定范围内均能有效降低激波阻力,本文认为控制过程中SMA鼓包挠度稳态误差小于5%即可达到要求。
本文训练了一种具有双向记忆效应的SMA鼓包,在温度升高时鼓包挠度减小,降温时挠度增加。搭建了SMA鼓包测试控制平台,通过实验获得了该SMA鼓包的温度/挠度迟滞曲线。基于KP迟滞模型对SMA鼓包的迟滞特性进行建模,利用粒子群算法完成了迟滞模型的参数辨识。在辨识得到的迟滞模型基础上,使用递推法推导了迟滞逆模型。设计了2种PID控制方案,并进行了仿真与实验研究。
1 SMA鼓包训练与测试
SMA鼓包的材料是等原子比NiTi合金,厚度0.5 mm,长宽尺寸为290 mm×30 mm,其中变形区域的长度为230 mm,如图1所示。与单程记忆效应不同,形状记忆合金的双程记忆效应不是材料的固有属性。在经过高温热处理后形状记忆合金往往只具有受热恢复形状的单程记忆效应。要使形状记忆合金获得双程记忆效应还需要经过热机械循环的训练过程。目的是在形状记忆合金马氏体相中引入位错,利用特殊排列的位错形成应力场引起冷却过程中马氏体变体在某些方向上择优选取,从而诱发双向记忆效应[18]。本文采用恒应力下相变循环的训练方法。训练装置如图2所示。

图1 SMA鼓包Fig.1 SMA bump

图2 SMA鼓包训练装置Fig.2 Training apparatus of SMA bump
鼓包测试控制平台由固定夹具、加热棒、液氮罐、激光位移传感器、热电偶、固态继电器、采集卡和计算机组成,实验装置如图3所示。
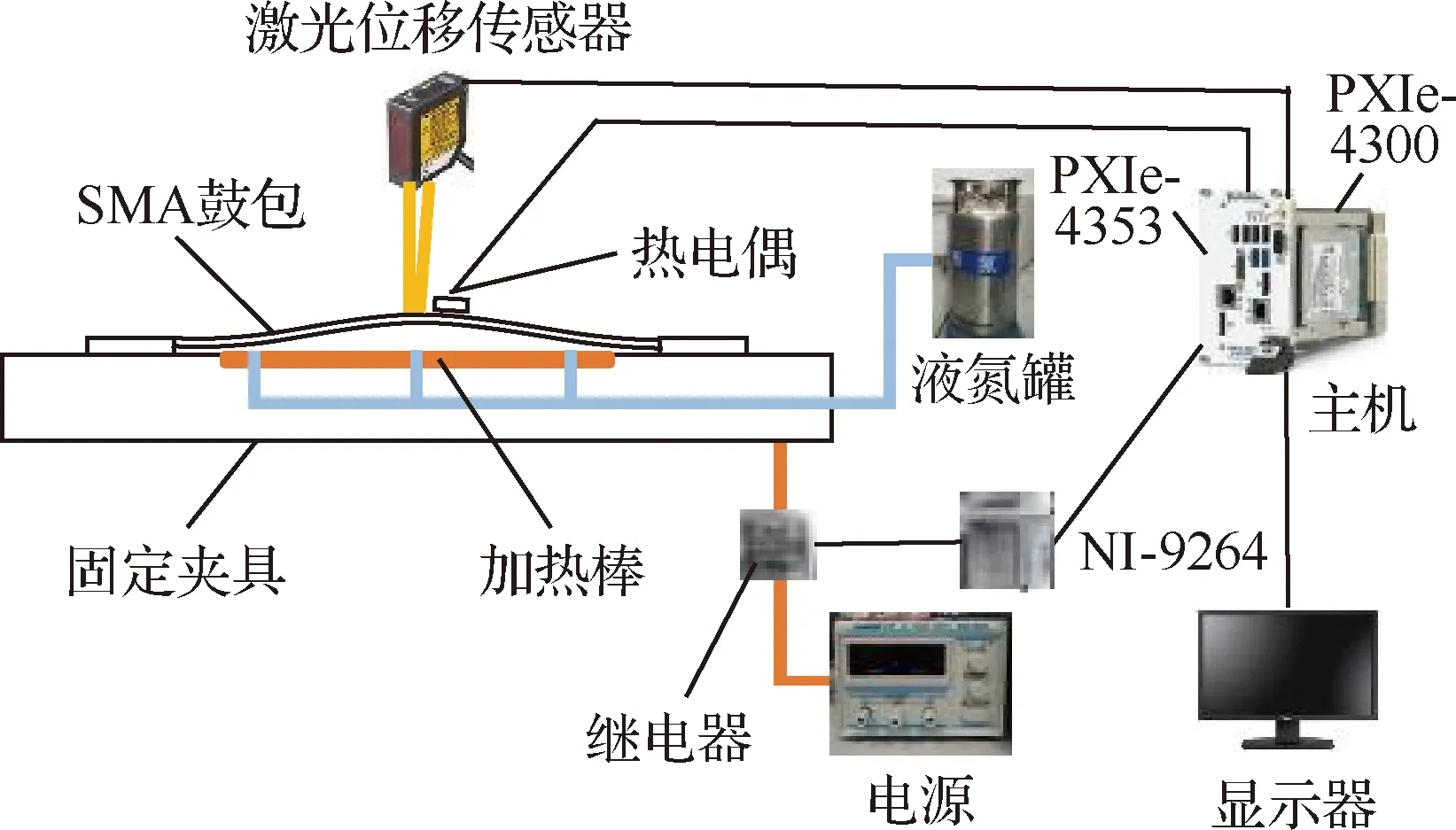
图3 SMA鼓包测试控制实验Fig.3 Test and control experiment of SMA bump
采用热辐射的方式对鼓包进行加热,利用液氮罐气体阀的气体对鼓包加速降温。在室温25 ℃ 下进行实验,通过Labview编写的采集程序得到了SMA鼓包中心点温度/挠度的迟滞曲线,如图4所示。
从图4中可以看出SMA鼓包的最大可回复位移约为6.1 mm,为鼓包变形区域的2.65%。
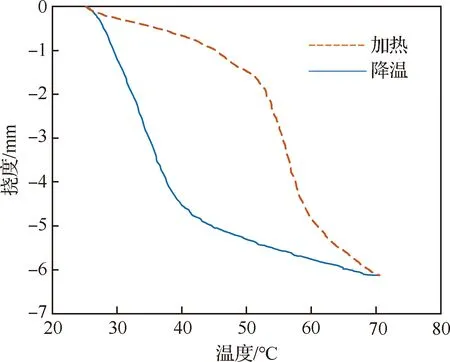
图4 SMA鼓包迟滞曲线Fig.4 Hysteresis loop of SMA bump
2 SMA鼓包迟滞模型
2.1 Krasnosel′skii-Pokrovskii模型
Krasnosel′skii-Pokrovskii(KP)模型是由M.A.Krasnosel′skii和A.V.Pokrovskii两位学者共同提出的一种基于迟滞算子的迟滞模型。KP模型是由Preisach模型改进而来,它们的基本思想都是认为迟滞现象是由一系列迟滞算子叠加而成,与Preisach模型不同之处在于将Preisach算子上升和下降边界的阶跃函数改为类似饱和函数,其数学表达式为
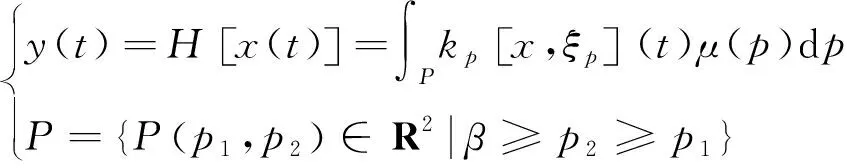
(1)
式中:x(t)与y(t)为KP模型的输入与输出;H(·)为KP函数;kp[x,ξp](t)为KP迟滞算子;ξp为KP算子输出的前一个极值的记忆值;μ(p)为Preisach平面的密度函数;P为Preisach平面积分区域;p1和p2分别为Preisach 平面内点的横、纵坐标;β为模型的最大输入。
经典KP算子如图5(a)所示,然而SMA鼓包在温度升高时挠度减小,温度降低时挠度增加,形成的是一个顺时针的迟滞环,且全部位于第4象限,需要改进KP迟滞算子,改进后的迟滞算子如图5(b)所示,图中a为迟滞环上沿与下沿横坐标差值。
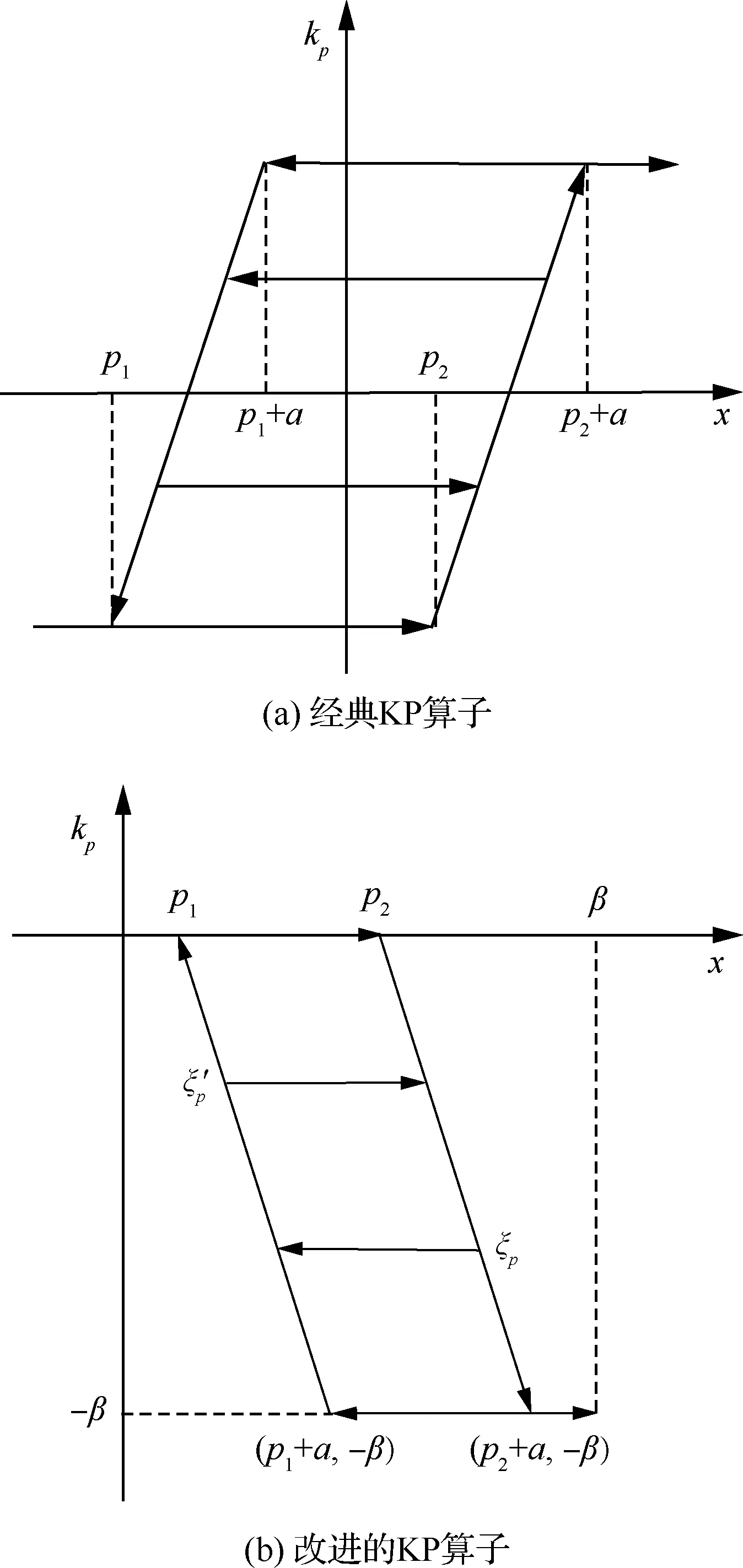
图5 KP算子Fig.5 KP operator
此时KP迟滞算子的数学表达式为
kp[x,ξp](t)=
(2)
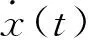
(3)
r(x)为迟滞算子上升沿和下降沿的边界函数,其表达式为

(4)
由于KP函数为积分形式不便于计算,可以根据数学积分的意义将Preisach平面离散化,将原函数中的平面积分转化为代数求和的形式。方法是用l条均匀分布的水平线与竖直线将积分区域Preisach平面分成如图6所示网格。离散化后的网格数目为N=(l+1)(l+2)/2,每个网格左下节点坐标(xi(t),xj(t)),即为式(2)中的(p1,p2),且有
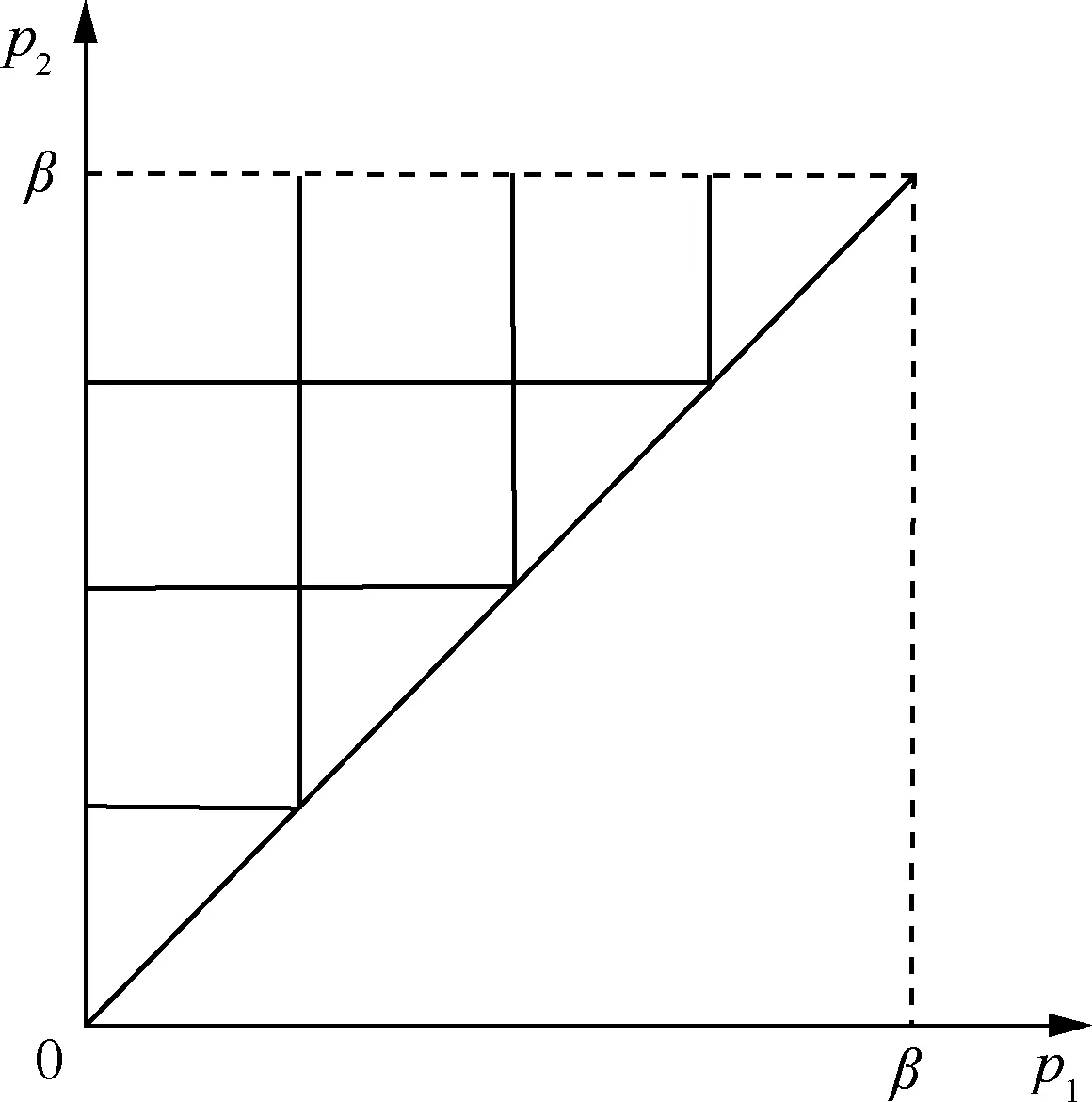
图6 离散化的Preisach平面Fig.6 Discretized Preisach plane
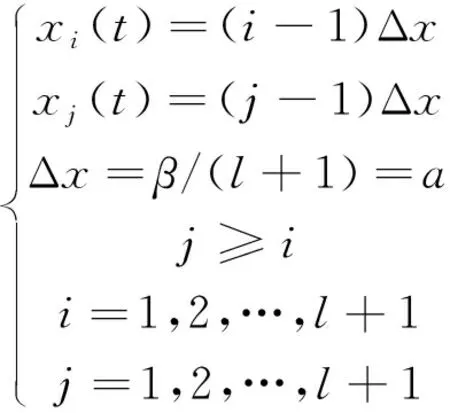
(5)
式中:i,j分别为第i个和第j个网格线;Δx为网格的宽度。
经过离散化后式(1)可以写成以下离散形式:
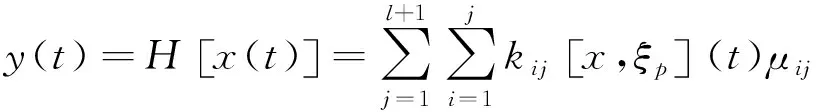
(6)
式中:kij[x,ξp]为各网格左下节点所对应的迟滞算子,如图7所示;μij为各网格对应的平均密度。迟滞模型的输出y(t)等于所有KP算子kij[x,ξp](t)乘以对应的平均密度μij所得积的叠加。从式(6)可以看出l值越大迟滞系统的输出值与实际输出值误差越小,模型的精度越高;同时也会导致计算量加大,模型辨识难度增加。应合理选择参数l的大小。
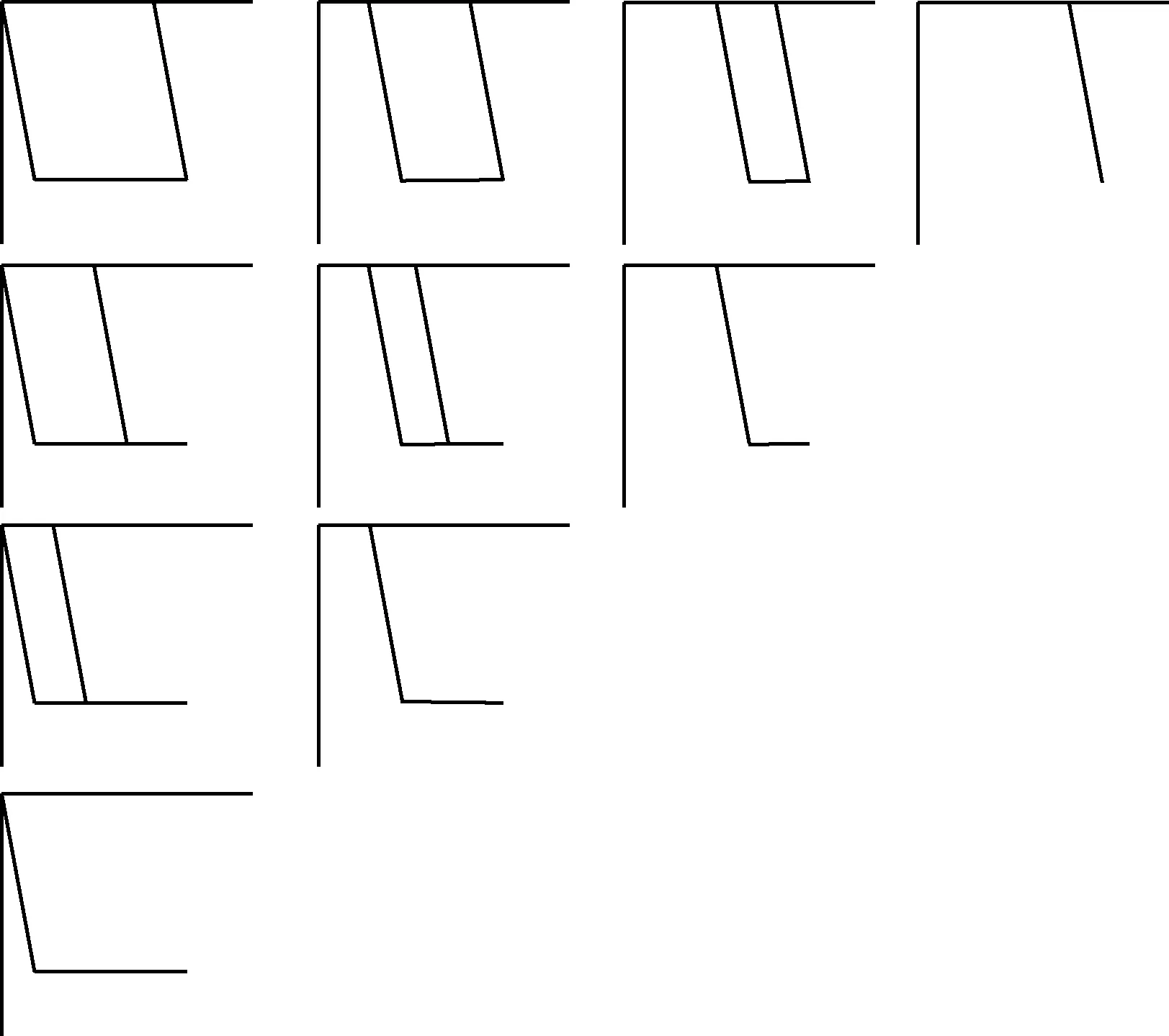
图7 各网格KP算子Fig.7 KP operator for each grid
2.2 KP模型参数辨识
粒子群算法(Particle Swarm Optimization,PSO)是一种全局寻优算法,粒子群算法因其容易实现、精度高、收敛快等优点,在系统辨识中得到了越来越多的应用。本节使用粒子群算法对KP模型的密度参数μij进行辨识。
2.2.1 粒子群算法
粒子群算法最早由Eberhart与Kennedy在1995年提出,该算法起源于对鸟群觅食行为的研究[19]。粒子群算法由初始化随机解出发,通过计算每个粒子所对应的适应度函数值来判断个体最优解与种群最优解,从而更新粒子速度和位置,通过不断迭代,直到找到全局最优解。
2.2.2μij参数辨识
为了方便计算与书写,将kij[x,ξp](t)记为kij,令
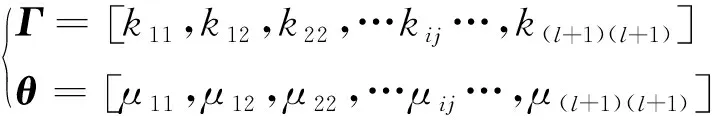
(7)
则式(6)可表示为
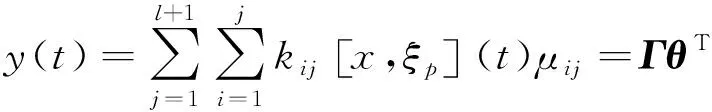
(8)
粒子群算法的适应度函数为
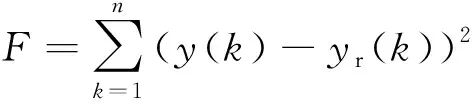
(9)
式中:y(k)为KP模型的输出值;yr(k)为第1节中测得的SMA鼓包在当前温度下的实际挠度;n为用于参数辨识的样本个数。粒子群算法用来求解该适应度函数的最小值。
由于在50~65 ℃区间SMA鼓包的迟滞曲线斜率变化较大,需将Preisach平面划分得较密,经过多次尝试比较,取l=39较为合理,在保证模型精度的同时也能兼顾计算时间。通过粒子群算法辨识得到的密度参数μij如图8所示。
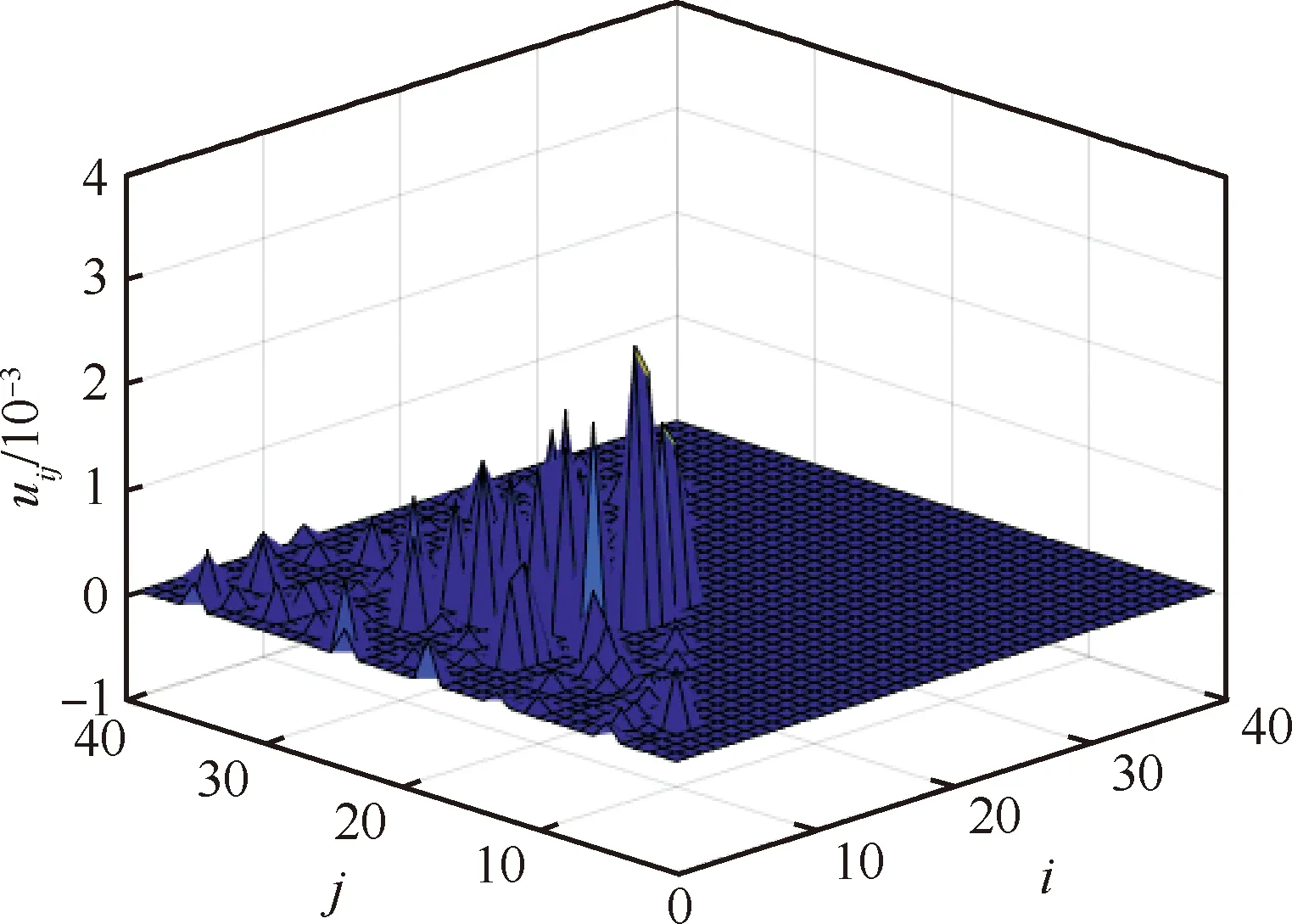
图8 密度参数μij在Preisach平面的分布Fig.8 Distribution of density μij in Preisach plane
将辨识得到的密度参数μij代入到KP迟滞模型中,可以得到SMA鼓包迟滞模型的温度/挠度迟滞曲线,如图9所示。图中实线为实验数据,虚线为模型输出。图10为SMA鼓包迟滞模型与实验数据的误差曲线,最大误差为0.107 mm,出现在迟滞曲线斜率变化较大处。图11 为迟滞模型动态特性,从图中可以看出迟滞模型不仅能够反映迟滞现象的主环信息,也能反映迟滞现象的次环信息。

图9 迟滞模型辨识结果Fig.9 Identification results of hysteresis model

图10 迟滞模型误差Fig.10 Error of hysteresis model
图11 迟滞模型动态特性Fig.11 Dynamic characteristics of hysteresis model
3 SMA鼓包控制策略
本节基于上文辨识得到的KP迟滞模型,提出了2种PID控制方案,在MATLAB中进行了仿真研究,并进行了SMA鼓包挠度控制实验。
3.1 迟滞逆模型
在迟滞非线性系统控制中,常常采用迟滞逆模型补偿来减小或消除系统中迟滞现象对控制精度的影响。求解逆模型的目标是:在某一时刻t,给定一个期望输出yd(t),找到一个使迟滞模型输出y(t)等于期望输出yd(t)的输入信号x(t)。本文基于前文得到的SMA鼓包迟滞模型通过递推法来推导迟滞逆模型。具体流程如下:
1) 设当前迟滞模型的输入为x0,输出为y0,期望输出为yd。
2) 若y0>yd(期望输出小于当前模型输出)
①x1=x0,y1=y0。
②x1=x1+dx(系统是递减的,应当 增加一个步长),y1=H(x1)。
③ 若y1>yd,返回执行 ②
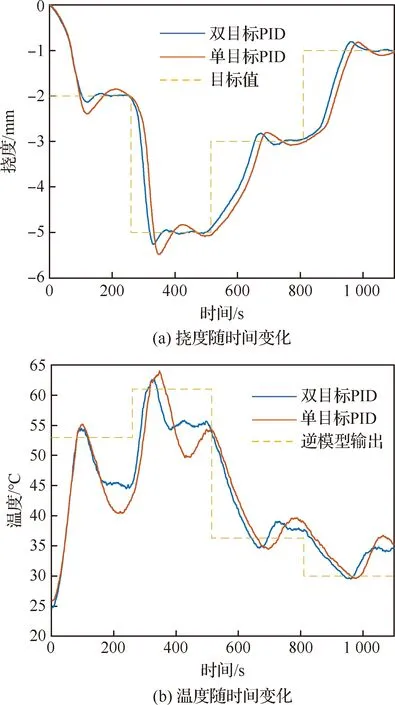
④ 当首次满足y1 3) 若y0 ①x1=x0,y1=y0。 ②x1=x1-dx(系统是递增的,应当减小一个步长),y1=H(x1)。 ③ 若y1 ④ 当首次满足y1>yd时停止循环,此时xd=x1即为迟滞逆模型的输出值。 由递推关系可知递推步长dx越小,通过计算得到的逆模型输出值与真实值误差越小。同时正模型离散化线数l越大,逆模型的精度也越高。应根据实际控制系统来合理选择dx的大小,本文取dx=0.1时,得到的迟滞逆模型如图12所示。图13为迟滞逆模型误差;最大误差发生在降温初期,此时温度变化较快而挠度变化较小,最大误差为0.719 ℃,相对误差为1.05%,迟滞逆模型已满足实际控制需要。 图12 迟滞逆模型Fig.12 Hysteresis inverse model 图13 迟滞逆模型误差Fig.13 Hysteresis inverse model error PID控制是一种广泛应用于工程实践的控制方案,其结构简单,易于实现,使用灵活[20]。其控制规律为 (10) 式中:kp为比例系数;Ti为积分时间常数;Td为微分时间常数;e(t)=yd(t)-y(t)为系统跟踪误差。 本文将KP迟滞模型与PID控制相结合,设计了2种控制方案,控制器设计框图如图14所示。图中:T(t)为系统当前温度;eT为温度跟踪误差;ey为挠度跟踪误差。第1种为无迟滞补偿的单目标PID控制,期望挠度yd(t)为控制目标,跟踪误差e(t)为期望挠度yd(t)与实际挠度y(t)的差值。第2种为迟滞逆模型前馈补偿的双目标PID控制,PID控制目标为期望挠度yd(t)与逆模型输出值xd(t),通过2个独立的PID算式计算,将2个算式的值按权重相加得到继电器的PWM(Pulse Width Modulation)占空比,位移与温度的权重分别为0.7与0.3,同时由于温度反馈只起补偿作用故移除温度反馈PID算式中的积分项。 图14 控制器设计框图Fig.14 Controller design block diagram 本文采用传递函数与迟滞模型串联的方式进行仿真研究。加热棒对SMA鼓包进行热辐射加热的过程可以简化为一个一阶惯性纯滞后模型,其系统输入为继电器PWM占空比,系统输出为温度。其传递函数表达式为 (11) 式中:K为系统的静态增益;T为系统的时间常数;τ为系统的纯滞后常数。 对SMA鼓包加热的飞升曲线如图15所示,由Cohn-Coon公式可以确定传递函数中的各项系数。其中K=1.22,T=102.2,τ=15.6。于是传递函数的具体表达式为 图15 鼓包加热飞升曲线Fig.15 Ascending curve of bump (12) 设初始点SMA鼓包挠度为0,表1为控制目标和迟滞逆模型输出值。图16反映了2种控制方案控制过程中鼓包挠度和温度的变化。仿真结果表明,迟滞逆模型前馈补偿双目标PID控制较无迟滞补偿的单目标PID控制到达稳态需要的时间更少,超调量更小。 表1 控制目标Table 1 Control targets 图16 仿真结果Fig.16 Simulation results 控制实验装置如图3所示,在室温25 ℃下进行实验,初始挠度为0,控制目标如表1所示。图17为实验过程中挠度与温度的变化。从图17(a)中可以看出各阶段双目标PID控制与单目标PID控制相比能更早到达稳定状态且误差更小。以第1阶段为例,当鼓包挠度与目标值相差较大时,2种算法输出的PWM占空比相同;当系统出现超调时由于系统热惯性与PID算法积分项的作用单目标PID算法超调量较大,此时双目标PID算法由于温度反馈的作用,其输出的PWM占空比小于单目标PID算法输出的PWM占空比,故超调量减小;同理当鼓包挠度再次小于目标值,此时鼓包温度已小于逆模型输出值,双目标PID算法输出的PWM占空比大于单目标PID算法输出的PWM占空比,故能够快速使SMA鼓包处于稳定状态。由于是以SMA鼓包的挠度控制为目标,同时考虑到系统鲁棒性,在双目标PID控制算法中仍以位移反馈作为主要权重,温度反馈仅有补偿作用,稳定状态下鼓包温度无需达到迟滞逆模型输出值。 图17 实验结果Fig.17 Experimental results 对于鼓包响应速度,2种控制方法的响应时间大致相同,具体来说在第1、第2升温阶段,鼓包响应速度受制于加热棒功率,而大幅提升加热棒功率会导致控制系统稳定性下降,考虑到激波控制鼓包主要应用于巡航状态的超临界机翼,巡航状态下鼓包外形变化频率较低,故本文中的响应速度以能达到应用需求。第3与第4阶段为降温阶段,鼓包响应速度受制于环境温度,而在实际应用中,由于不存在气动加热,环境温度较低,鼓包响应速度会得到明显提升。 表2为部分时域性能指标。迟滞逆模型前馈补偿双目标PID控制与单目标PID控制相比各阶段误差均大幅减小。单目标PID控制最大相对误差为第4阶段的10.3%,双目标PID控制最大相对误差为第4阶段的2.2%,减小了78.6%,双目标PID控制的相对误差已达到小于5%的要求。 表2 时域性能Table 2 Time domain performance 1) 为了解决固定挠度鼓包工作范围较窄的问题,训练了一种具有双程记忆效应的SMA鼓包,温度升高时挠度减小,温度降低时挠度增大,其最大可回复位移为6.1 mm,为鼓包变形区域的2.65%。 2) 针对SMA鼓包在变形过程中温度/挠度的迟滞非线性现象,基于KP迟滞模型进行了建模研究;使用粒子群算法完成了模型的参数辨识。辨识得到的模型与实验数据最大误差为0.107 mm。 3) 以迟滞模型为基础,采用递推法得到迟滞逆模型,为控制系统的迟滞补偿打下了基础。 4) 提出了2种PID控制方案,一种为无迟滞补偿的单目标PID控制,一种为迟滞逆模型前馈补偿的双目标PID控制。仿真与实验结果表明,后者控制性能明显优于前者,已基本满足需求。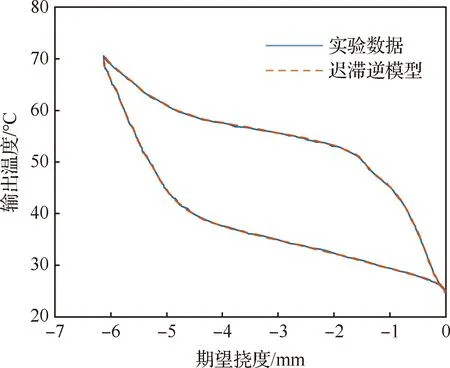

3.2 控制方案
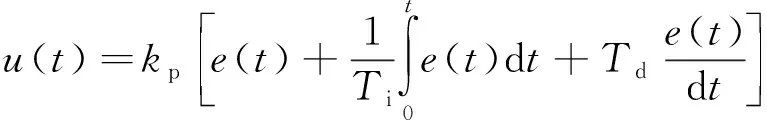
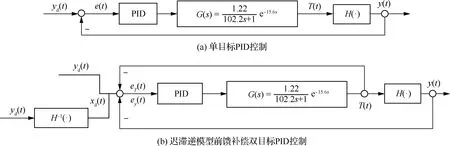
3.3 系统传递函数


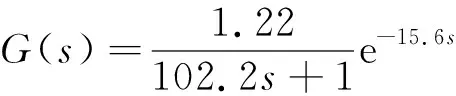
3.4 控制仿真
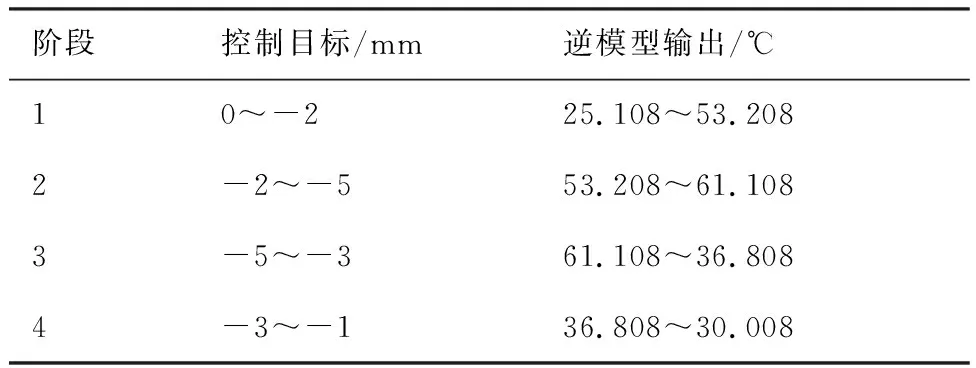
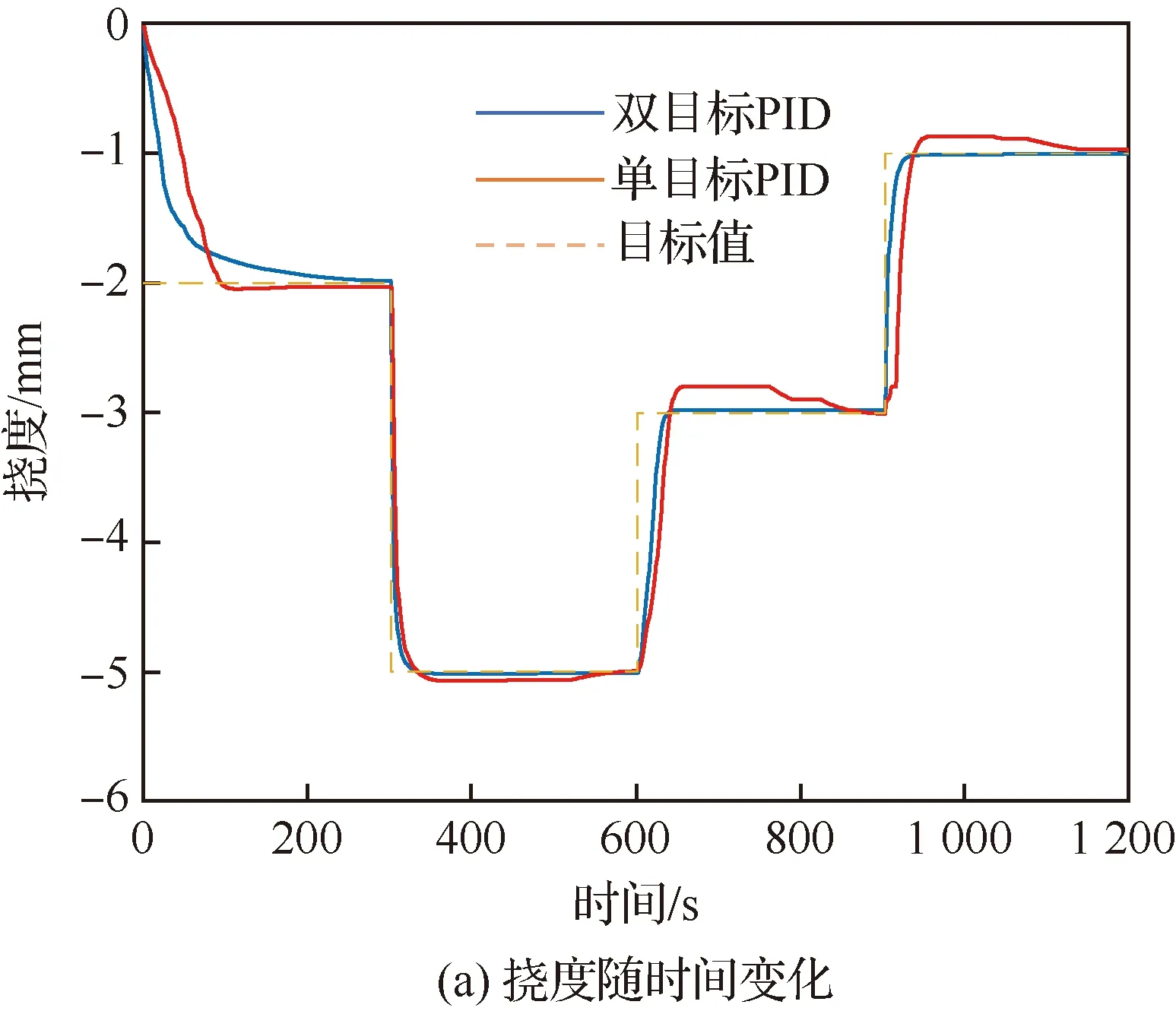
3.5 SMA鼓包变形控制实验

4 结 论

