软式空中加油对接约束力不确定性分析

张国斌，张青斌，丰志伟，陈青全，杨涛

国防科技大学 空天科学学院，长沙 410073

空中加油是指加油机和受油机在飞行过程中以管道形成对接，然后将燃油输送到受油机的过程。通过空中加油操作，可以大幅提高受油机的飞行半径和留空时间，从而提升受油机的使用效能[1-2]。空中加油主要有2种方法：软管锥套式空中加油和伸缩管式空中加油，这2种方法也分别被称作软式空中加油和硬式空中加油。

如图1[3]所示，在软式空中加油过程中，加油机保持一定的速度水平飞行，从加油吊舱中释放输油软管，软管末端装有伞状锥套[1]，在气动力的作用下，锥套稳定于加油机后侧的某个区域。在受油机机头侧方位置安装有受油管，驾驶员操纵受油机使受油管插入锥套完成对接。对接完成后，燃油阀门打开，燃油通过加油机传送至受油机。相比于硬式空中加油，软式空中加油设备轻便小巧，输油过程中允许加油机与受油机间存在一定的相对运动，安全性得到了一定的提高。然而，由于完成对接后的相对运动控制难度大、对接点结构薄弱，软式空中加油目前仍是一项危险性高、成功率低的空中作业项目，对飞行员的技术水平和飞机性能均有较高的要求。

图1 软式空中加油[3]Fig.1 Diagram of hose-drogue aerial refueling[3]

在软式空中加油过程中，位于受油机侧方的受油管需要保持锥套相对受油机静止，往往要承受较大的约束力，而其结构尺寸又小，在输油过程中容易断裂或从锥套中脱离。长期的空中加油实践和仿真均表明：加油机和受油机间的相对运动、气流与输油软管间的流固耦合作用以及其他干扰因素会诱发输油软管产生甩鞭现象(Hose Whipping Phenomenon，HWP)[4]。甩鞭现象表现为输油软管的剧烈甩动，同时受油管和锥套的连接处还会产生较大的瞬时载荷。由于甩鞭现象的出现，空中加油过程中受油管极有可能因为受到较大载荷而出现断裂，进而导致加油任务失败，断裂的油管甚至还有可能飞入受油机进气道酿成惨重的空中安全事故。因此，建立软式空中加油对接状态下的动力学模型，并采用数值仿真手段获取受油管受到的对接约束力具有重要的工程应用价值。

对输油软管的建模多采用离散的质点模型或基于球铰连接的刚性杆模型。胡孟权等[5]将输油软管质点离散化，研究了大气紊流对油管锥套组合体运动的影响。Ro和Kamman[6]将输油软管离散为若干采用球铰连接的刚性杆，研究了加油系统的动力学特性。王海涛等[7]提出了一种长度可变的多级串联“球-杆”动力学模型，基于此模型研究了空中加油过程中的控制策略。在串联“球-杆”动力学模型的基础上，王海涛等[8]通过在相邻两刚体间引入弯曲恢复力，建立了软管锥套组合体的动力学模型，依靠该模型对甩鞭现象进行了初步分析。采用这类集中参数模型可以较为便捷地建立起输油软管的动力学模型，并能较好地反映软管在加油过程中的动力学特性，但是难以描述油管上连续分布的应力和应变，与实际情况的差异性较大。在输油软管的振动控制研究中，Liu等[9-10]利用偏微分方程来描述加油过程中输油软管的动力学特性。这种方法的控制方程在小变形假设下推导，仅考虑输油软管的横向振动，针对输油软管的振动控制问题取得了较好的效果。采用非线性有限元建立输油软管动力学模型也是目前常用的一种建模方法。尽管理论推导较为复杂，数值仿真的计算量也稍大，但是非线性有限元基于连续介质力学对输油软管进行描述，理论基础更加坚实，能够更加真实地反映输油软管本身的物理特性。Zhu和Meguid[11]开发了一种三节点梁单元用于软式空中加油的动力学仿真，并通过试验验证了模型的有效性。刘钒[12]基于绝对节点坐标法(Absolute Nodal Coordinate Formulation，ANCF)[13-14]建立了输油软管动力学模型，对软管锥套组合体在给定流场的稳定拖曳姿态和释放过程进行了研究。在输油过程中，燃油相对油管的流动会形成较大的惯性力，但目前考虑燃油流动的动力学模型还较少。通过采用ALE(Arbitrary Lagrange-Euler)方式描述管内流体单元，并结合ANCF方法，洪迪峰[15]建立了一种可描述结构大位移和大转动的输流管道的动力学模型，该模型与ANCF结构单元的兼容性极好，易于进行系统动力学的组装。空中加油过程的动力学建模涉及的学科领域广、建模难度大，传统的集中参数模型难以适应几何非线性条下柔性体高精度建模的要求。非线性有限元技术在近几十年来实现了飞速的发展，结合计算多体动力学建模技术可建立刚-柔-液耦合的高保真空中加油动力学模型。

飞行速度、输油软管长度、输油软管力学特性参数和其他不确定因素均可对空中加油过程中受油管和锥套间的约束力造成影响。这类不确定因素在某一区间内服从一定的概率分布，如要获取所有情况下对接约束力大小，需要仿真数目极大的工况，从而消耗大量的计算资源和计算时间。多项式混沌展开是一种基于谱分析的方法，可以在输入参数满足一定概率分布的情况下快速给出输出参数的期望值、方差和概率分布，而不需要大量的抽样计算，能够极大地提高分析计算的效率[16]。

本文首先基于绝对节点坐标法建立输油软管的非线性有限元模型，利用ALE描述方法在输油软管单元控制方程上耦合燃油的动力学方程，结合多体系统建模方法建立空中加油系统刚-柔-液耦合的多体动力学模型，给出受油管指定截面所受约束力的计算方法；其次，引入基于多项式混沌展开的不确定性分析方法；再次，通过动力学仿真说明甩鞭现象对于对接约束力的影响，对比分析出现甩鞭现象时输油软管上的受力分布特点；最后，在不确定性条件下，基于多项式混沌方法给出在不同巡航高度下，加油机与受油机有无相对运动时，对接约束力的期望范围。

1 动力学建模

1.1 坐标系定义与基本假设

如图2所示，在软式空中加油过程中，加油机始终保持匀速平飞状态，因此，将固定于加油机上的笛卡尔坐标系oxyz认定为惯性系，其中o点为输油软管在加油机上的释放点，ox沿加油机水平飞行方向，oy轴指向重力反方向，oz轴按右手法则确定。在空中加油多体系统中，设输油软管oA采用球铰分别与加油机和锥套连接于o点和A点。将锥套视为刚体，质心为o1，体坐标系为o1x1y1z1，在对接的初始状态，o1x1y1z1与oxyz各坐标轴平行。弯曲和拉压是输油软管在加油过程中的主要变形模式，采用能够描述弯曲和拉压变形的绝对节点坐标法梯度缩减梁单元(Gradient Deficient ANCF Beam)对输油软管进行建模[17]，这种单元采用了欧拉-伯努利梁假设(梁截面始终垂直于中心轴线且保持为平面)。当油管中包含燃油时，根据弹性力学中对圆管受均布压力问题的推导[18]，油压所产生的应力分量平行于梁截面，本文认为油压不对梁单元的弯曲和拉压变形产生影响。在输油过程中，将管内燃油视为一维不可压缩的理想流体，并且流速处处相等。

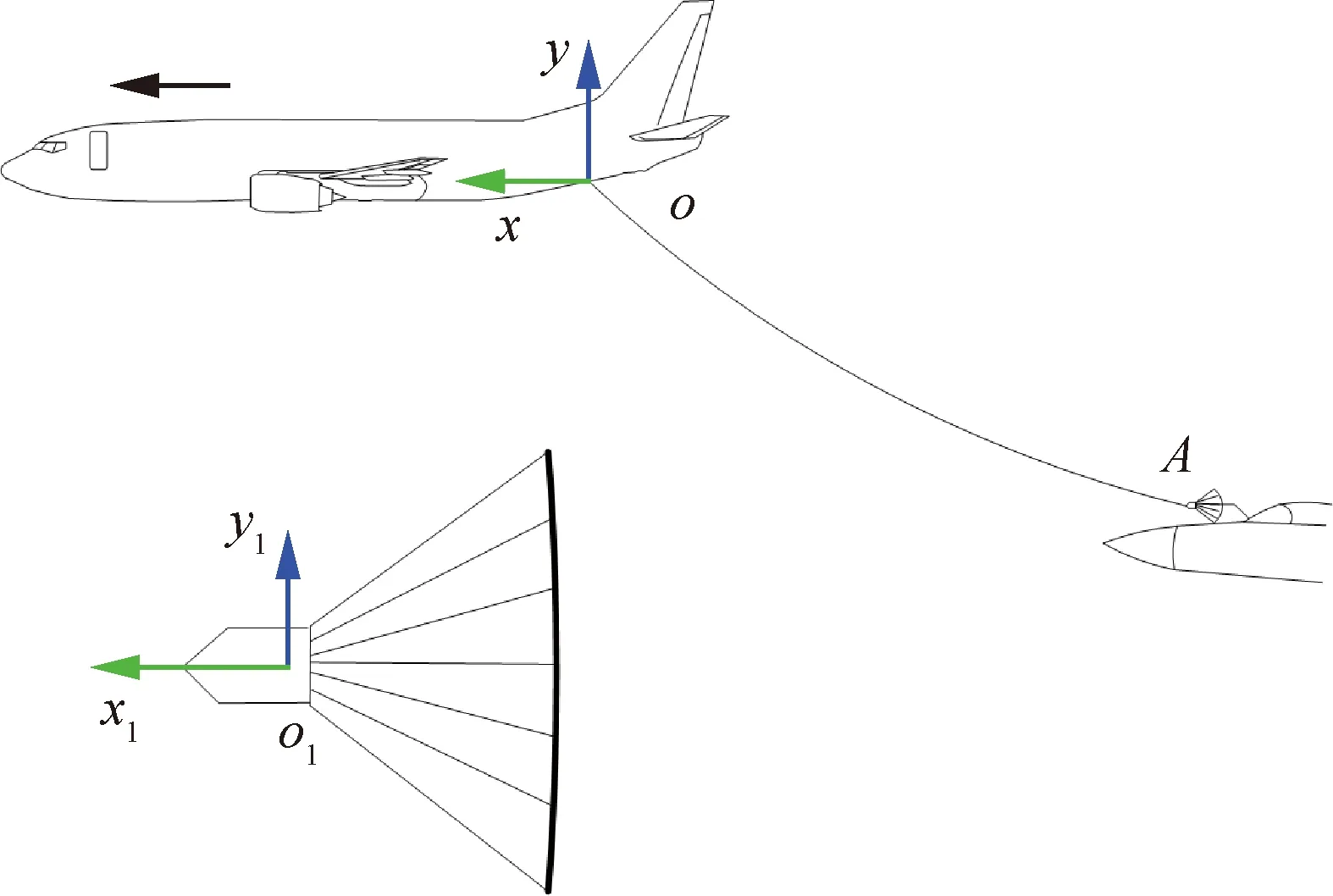
图2 空中加油系统坐标系定义Fig.2 Definition of coordinate frame of air refueling system

1.2 基于绝对节点坐标法的输油软管建模

绝对节点坐标法是由美国学者Shabana等[13]提出的一种柔性多体系统建模方法。绝对节点坐标法采用微分几何的方法描述连续体变形，引入的人为假设少，相比于传统方法具有更高的插值精度。此外，绝对节点坐标法具有质量矩阵为常数、数值稳定性好、易于与其他多体系统组合等特点，目前已经成为多柔体系统最为有效的建模方法之一[19-21]。

1.2.1 软管结构动力学模型

采用绝对节点坐标法梯度缩减梁单元建立输油软管结构的非线性有限元模型，该单元的参考构型坐标空间是一维的：只采用沿梁中心轴线的弧长s作为标定材料点的物质坐标，单元原长为L，如图3(a)所示。单元包含2个节点，节点坐标包含一个位置向量ri和梯度向量ri,s(i=1,2)，如图3(b)所示。绝对节点坐标法中所有矢量均在惯性系下表示。

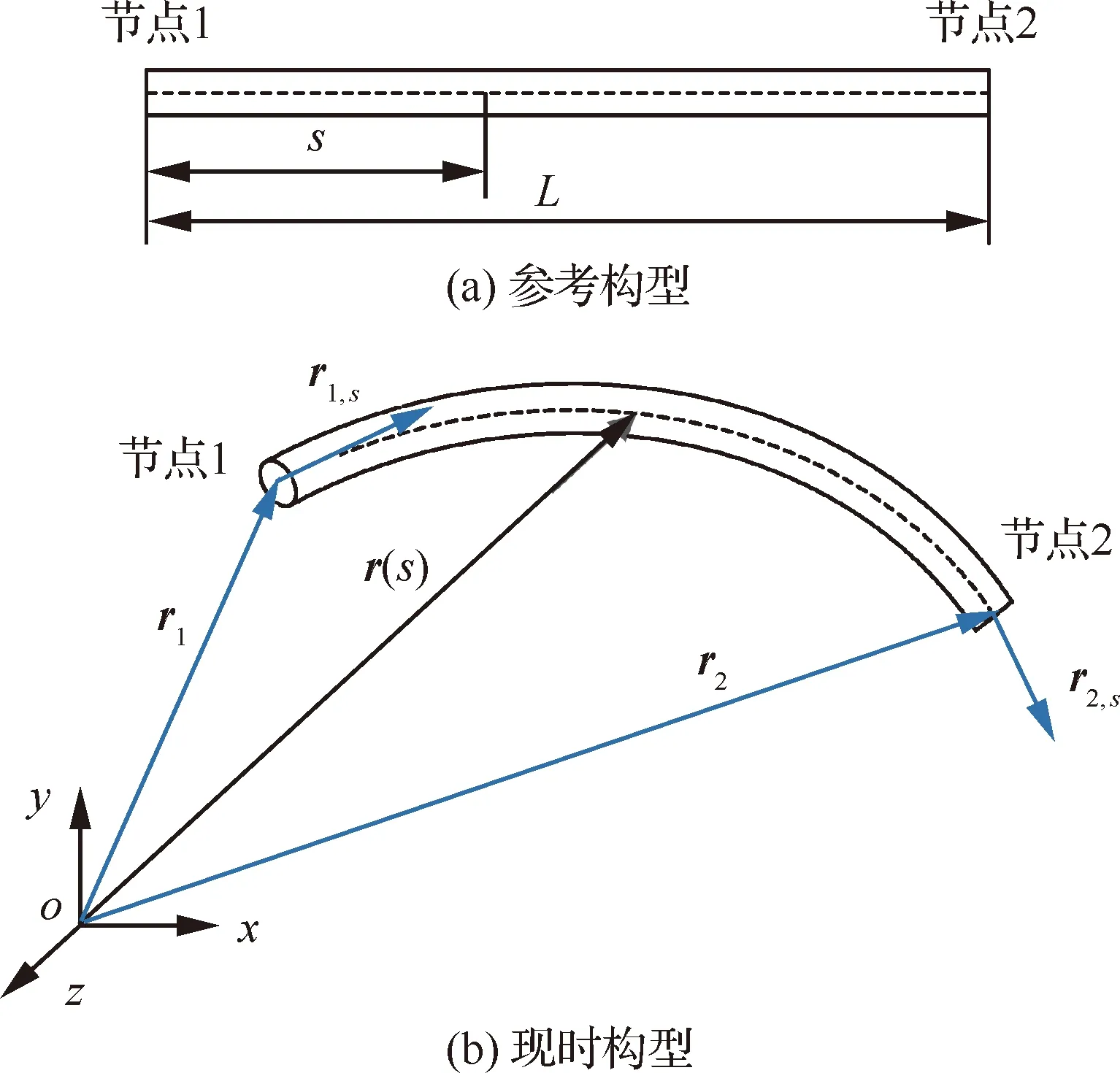
图3 绝对节点坐标法缩减梁单元Fig.3 Gradient deficient ANCF beam

基于有限元技术，单元内任意物质点s在当前构形的空间位置向量用形函数矩阵和节点坐标向量表示形式为

r(s)=N(s)qe

(1)

式中：qe为单元节点坐标向量；N(s)为形函数矩阵；qe的具体形式为

(2)

N(s)具体为

(3)

其中:I为3×3单位阵;4个形函数分别为

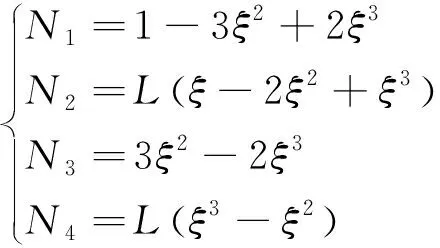
(4)

式中：ξ=s/L。

采用虚功原理或第2类Lagrange方程均可以推导出单元的动力学方程：

(5)

(6)

式(6)在参考构型中积分，其中：ρh和Ah分别为输油软管在变形前的密度和截面积。

单元的广义内力由单元变形能V对单元节点坐标求导得到，即

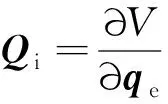
(7)

由于采用了欧拉-伯努利梁假设，并考虑到输油软管截面形状为圆环，单元的变形能为

(8)

式(8)同样在参考构型下积分，其中：E为输油软管材料的杨氏模量；Ih为输油软管截面惯性矩；ε为轴向应变；κ为曲率。通过微分几何可知

(9)

(10)

式中：rs表示r对s求一次偏导；rss表示r对s求2次偏导。由虚功原理，作用在材料点s上的外力F所做的虚功为

(11)

故力F所对应的广义力为

QF=N(s)TF

(12)

由重力g所产生的广义力为

(13)

1.2.2 管内燃油动力学模型

加油过程中，输油软管中的燃油可认为是一维不可压缩的理想流体，将燃油相对油管的流速设为U。如图4所示，在输油软管单元两端的节点上，燃油的物质坐标分别为

图4 管内燃油模型Fig.4 Model for oil inside the hose

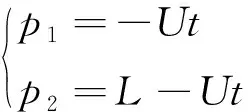
(14)

式中：U为燃油相对油管的流速；t为流动时间。

软管内燃油的运动学描述同样采用绝对节点坐标法实现，并与软管结构单元共用形函数和节点坐标。燃油物质点的物质坐标p与软管单元形函数参数s的关系为

s=p+Ut

(15)

式(15)表征了燃油在输油软管内的流动。

软管内燃油物质点的空间位置可由形函数表达为

r(p)=N(s)qe

(16)

对式(16)求物质导数，得到燃油物质点的速度和加速度分别为

(17)

其中：

(18)

不考虑燃油的黏性，基于虚功原理，燃油的惯性力所做虚功和重力所做的虚功之和为0，即

(19)

式中：ρo为燃油密度；Ao为油管空腔截面积。经过代数运算后可得

(20)

其中：

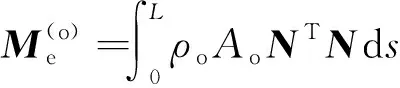
(21)

结合软管结构的动力学方程，可以得到考虑燃油流动的输油软管单元动力学微分方程为

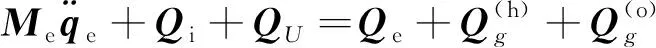
(22)

1.3 流场模型与气动力估算

1.3.1 流场模型

根据1.1节中的假设，由于采用固连于加油机上的惯性坐标系oxyz来度量空中加油过程中的所有物理量，故加油机后方流场可近似为直匀流叠加加油机尾涡流场。现有的尾涡流场模型包括Rankine vortex模型、Adapted vortex模型、Lamb-Oseen vortex模型、Smooth blending vortex profile模型和Hallock-Burnham vortex模型等[22-23]。在空中加油的仿真计算中，通常采用Hallock-Burnham vortex模型计算尾涡产生的速度场[24-25]。

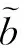
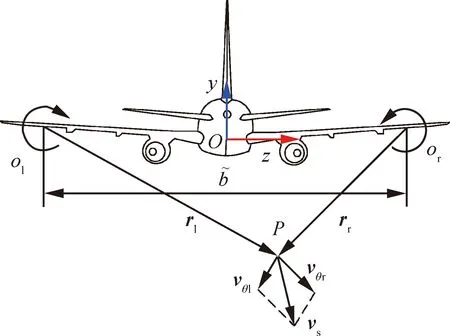
图5 尾涡速度场模型Fig.5 Model for wake vortex velocity field

(23)

(24)

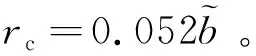
取加油机重量为185 t，平飞速度为105 m/s，飞机翼展为49.5 m，基于Hallock-Burnham模型计算由尾涡诱导出的流场，在尾涡涡心所在的铅垂面上，尾流场如图6所示。相比于加油机平飞速度105 m/s，尾涡所诱导出的最大速度小于12 m/s，二者的合成速度为105.7 m/s，可见尾涡对相对流动速度的影响较小。

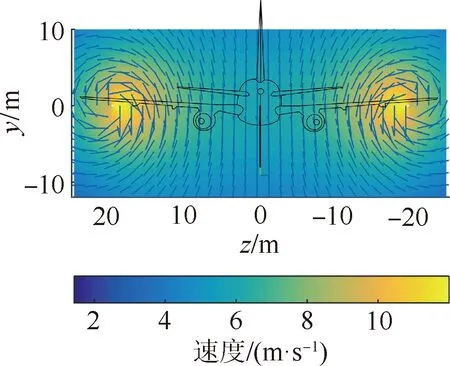
图6 尾涡中心所在截面的尾涡流场铅锤切面Fig.6 Vertical slice of wake flow fieldat wake center

1.3.2 气动力计算

输油软管微段dl受到的气动力可以表示为如下形式：

(25)

式中：Cd为输油软管受到的压差阻力系数；Cf为输油软管的摩擦阻力系数；ρa为气流密度；d为输油软管外径；vn为输油软管微段相对气流的法向速度；vt为输油软管相对气流的切向速度。采用试验公式[27-28]计算油管受到的摩擦力系数Cf和压差力系数Cd：

(26)

Cd=

(27)

式中：Ref和Rep为雷诺数，其计算式分别为

其中：ν为空气黏度系数。

结合式(12)，输油软管单元受到气动力所对应的广义外力为

(28)

式中：第1个积分式的积分域为当前构型；l为当前单元长度；第2个积分式的积分域为参考构型。在动力学程序中，对式(28)的积分可采用Gauss方法进行数值计算[29]。

为简化计算，假设锥套受到的气动力通过锥套质心，计算公式为

(29)

式中：v为气流相对锥套质心的速度；Sd为锥套的特征阻力面积；Cd为锥套的气动阻力系数。

1.4 多体系统组装与对接约束力求解

1.4.1 多体系统组装

利用绝对节点坐标法建立描述输油软管和燃油动力学的单元，对输油软管划分单元再进行组装后可得到输油软管部分的动力学方程为

(30)

式中：Mh为输油软管及内部燃油所对应的广义质量阵；qh为单元节点坐标对应的列向量；Qe为油管弹性内力所对应的广义力列向量；Qa为油管所受到的气动力列向量；QU为燃油流动所形成的附加广义惯性力；Qg为油管及内部燃油所对应的重力广义力列向量。当输油软管的划分单元数为ne时，广义质量阵Mh所对应的阶数为6(ne+1)。

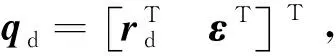
(31)

式中：md为锥套的质量；Jx、Jy和Jz分别为锥套在本体系上主惯量。锥套的动力学方程为

(32)

(33)

式中:λ0、λ1、λ2和λ3分别为姿态四元数ε对应的4个分量。

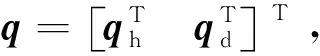
Φ(q)=012×1

对约束方程关于时间求一次导数，并利用式(33) 将四元数的导数替换为锥套角速度可以得到

继续关于时间求导可得

(34)

结合式(30)、式(32)和式(34)，可得空中加油多体系统动力学微分方程为

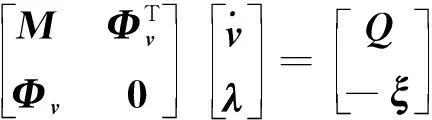
(35)

式中：

(36)

式(35)为指标1微分代数方程，可以通过常微分求解器做积分计算。

1.4.2 对接约束力求解

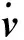
(37)

使广义约束力QΦ的分量对应于相应的广义坐标，则可得到相应的约束力分量。

在对受油管进行强度分析时，需要知道对接约束力作用于受油管截面的拉压力、剪切力及弯矩。由式(37)，可以推算得到受油管作用于锥套质心的约束力向量FΦ(投影在全局坐标系oxyz)及对锥套的约束力矩向量MΦ(投影在锥套本体系o1x1y1z1)。根据牛顿第三定律，可知锥套施加给受油管的力系可等效为作用位置在锥套质心的集中力-FΦ以及力矩-MΦ。在对接过程中，受油管与锥套连接为一体，令受油管的本体系与锥套本体系方向一致，如图7(a)所示，则受油管截面B-B受到的弯矩为

(38)

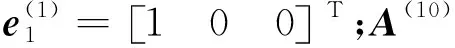
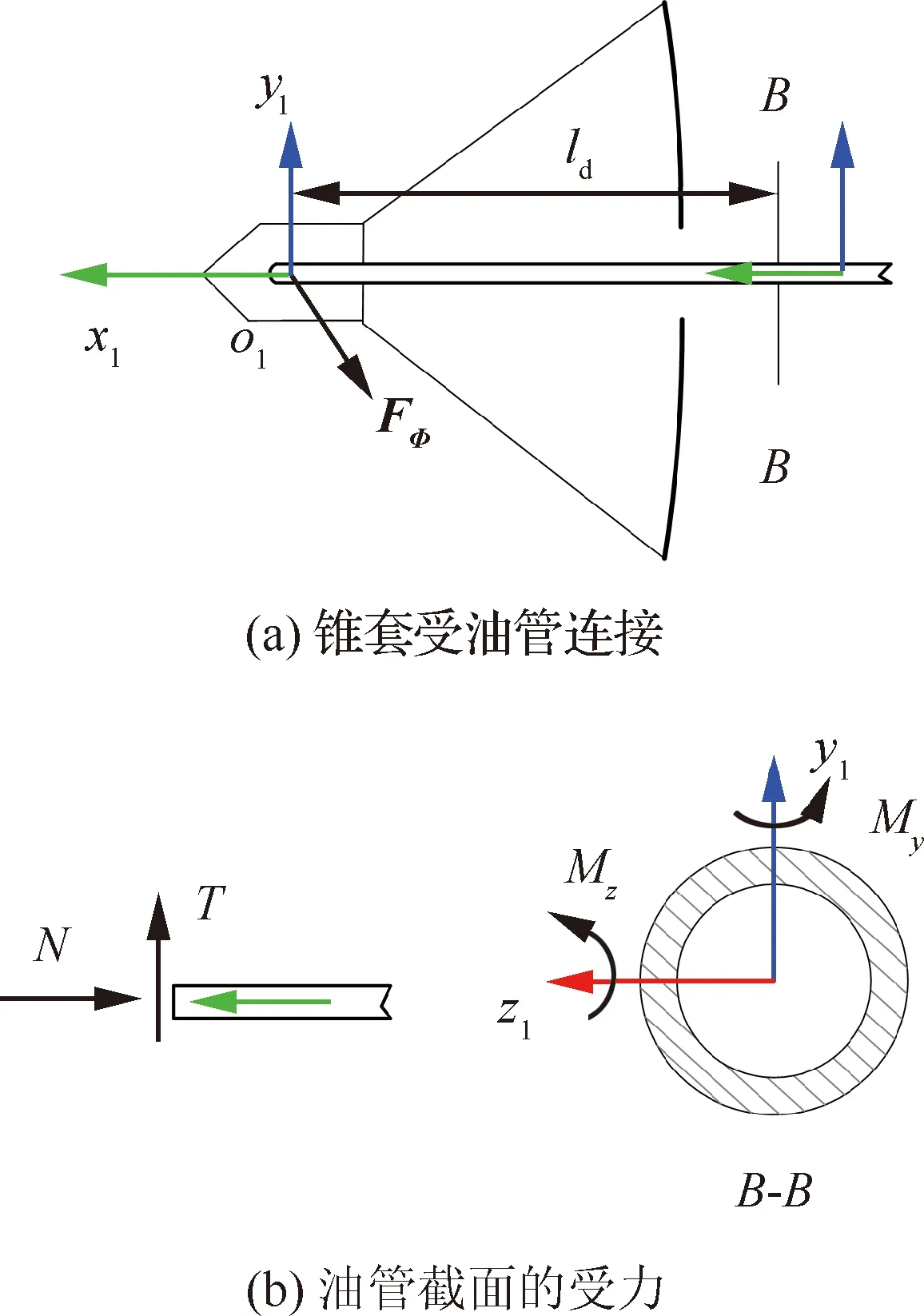
图7 受油管受力状态Fig.7 Force on oil tube

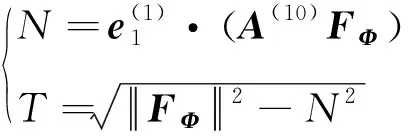
(39)

2 不确定性分析方法

空中加油过程对接约束力的求解需要涉及众多的输入变量，包括：飞行速度、输油软管长度、飞行高度和相对运动速度等。如果采用经典的Monte-Carlo方法，则需要规模巨大的仿真任务，耗费大量的计算资源和时间。高效的不确定性分析方法能够用较少仿真次数得到多个输入量在一定概率分布下输出量的统计特征，从而大大提高工作效率。多项式混沌方法是目前较为成熟的一种不确定性分析方法，在实际工程问题中得到了广泛的应用[31-33]。

2.1 多项式混沌展开理论

多项式混沌展开的基本思想是用含独立随机变量的正交多项式之和来近似表示随机过程[34]。即将系统输出量y和不确定输入向量x的关系表示为

(40)

式中：βi为常系数；φi(x)为多元多项式基函数；n为非常数多项式基函数的个数。

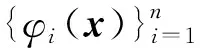
(41)

式中：〈·〉代表内积运算；Ω为积分域；γi=〈φi(x),φi(x)〉为标准化常量；δij为克罗内克张量。当给定随机变量的概率密度函数ω(x)后，定义正交多项式基的第1项φ0(x)=1，再基于Gram-Schimidt正交化方法，利用式(41)所定义的内积运算，对线性无关的函数系

{φi|φi(x)=xi,i=0,1,2,…}

做正交化处理，即可得到在给定概率分布下的正交多项式基。照此方法可知：正态分布随机变量对应的正交多项式基为Hermite多项式；均匀分布随机变量对应的正交多项式基为Legendre多项式；贝塔分布随机变量对应的正交多项式为Jacobi多项式。Legendre多项式的前4项如表1所示。

表1 前4项Legendre多项式Table 1 First four Legendre polynomials

若系统输入含有多个独立随机变量，则可将单变量对应的正交多项式按独立组合的原则连乘再相加得到多维随机变量的多项式混沌展开[33]：

(42)

式中：q为独立随机变量个数；βi1,…,iq为多项式混沌展开系数；nk(k=1,2,…,q)是变量xk的正交多项式最大阶数，基函数可表示为

ψi1,…,iq(x)=φi1(x1)φi2(x2)…φiq(xq)

其中：φik(xk)是随机变量xk的第ik次项。在不确定性分析问题的研究中，一般对式(42)按照最大阶次进行截断。若选定的最大阶次为p，则式(40) 中需要求的待定系数个数为

(43)

对系统输出量完成多项式展开后，由正交多项式的基本性质，系统输出量y的期望和方差分别为

E(y)=β0

(44)

(45)

2.2 多项式混沌展开系数计算

多项式混沌展开模型的系数确定是多项式混沌方法的核心步骤。现有的系数求解方法可分为嵌入法(Intrusive Method)和非嵌入法(Non-intrusive Method)[35]。嵌入法在使用时需要修改动力学模型，不适用于大型动力学仿真程序，而非嵌入法则不需要修改动力学模型，应用范围更广。

本文讨论非嵌入法中的随机响应面法[34]。对系统输入随机变量x构成的多维空间，每次动力学计算的输入向量就对应这个空间中的一个点，通常称这个点为采用点或配置点。要求解多项式混沌展开中的未知系数，需选取足够多的配点。对q维p阶多项混沌展开，随机响应面法的取点原则是：对每个变量取p+1阶多项式的根，然后将这些根进行组合，最后得到(p+1)q个采样点。将所有的采样点输入动力学仿真程序计算将得到(p+1)q个系统输出yi，参考式(40)，可以得到方程组：

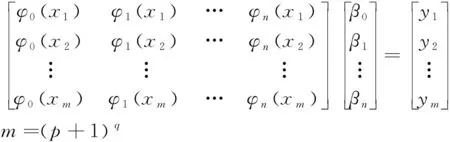
(46)

记式(46)为Hβ=y，则可对多项混沌系数进行最优估计：

β=(HTH)-1HTy

(47)

3 不确定性条件下的仿真分析

3.1节首先对正常对接与出现甩鞭现象时的对接情况进行对比分析。本文假设加油机飞行速度、输油软管长度和对接相对运动速度大小都服从指定区间的均匀分布。3.2节分析在不同高度下，油管长度和飞行速度为随机变量时，受油管指定截面上的拉压力、剪切力和弯矩的期望和标准差。3.3节分析不同高度下，受油机相对运动速度大小和输油软管长度为随机变量时，受油管指定截面的拉压力、剪切力和弯矩的期望和标准差。

3.1 甩鞭现象对应的约束力变化

本文针对某型加油机的空中加油过程进行研究。在500 m的飞行高度下，环境参数为：空气密度为1.17 kg/m3、空气黏度系数为1.79×10-5、重力加速度为9.8 m/s2。取加油机飞行速度为155 m/s，油管长度为24 m。其他参数如表2所示。油管划分单元数为10，通过仿真分别得到了在正常对接和受油机相对速度为(1, 0, 0)m/s(投影在oxyz系)时受油管某一截面约束力随时间变化曲线，如图8所示。从图8中可见，受油管截面的压力、剪力和弯矩都出现了明显的增大，特别是剪力和弯矩的增幅最为明显，出现甩鞭现象后最大弯矩增加至正常对接的6.1倍；从曲线的波动变化情况可以推测此时输油软管上出现了较高频率的振动。甩鞭现象对应的锥套油管组合体的运动过程如图9所示，图9中预测的输油软管位形与实际甩鞭现象中拍摄的照片吻合度较好[8]。

图8 受油管某考察截面的受力Fig.8 Force acting on the section of probe under investigation

图9 甩鞭现象对应的软管位形Fig.9 Hose configuration corresponding to HWP

表2 系统参数Table 2 System parameters

输油软管出现甩鞭现象和正常对接时的弯矩分布云图分别如图10(a)和图10(b)所示。从图中可见，输油软管最大截面弯矩均出现在靠近锥套的部分，相比于正常对接状态，出现甩鞭现象时输油软管弯矩明显增大。输油软管截面的压力如图11所示(注意图11中压为正、拉为负)，对比图11(a) 和图11(b)可知：发生甩鞭现象时，输油软管截面主要受压，在输油软管曲率较大的部位会出现较大的拉力；而在正常对接状态时，输油软管截面受拉，最大拉力出现在输油软管与加油机连接的部位；出现甩鞭现象时输油软管截面受到的拉压力会比正常对接时的拉压力偏大。

图10 油管截面弯矩Fig.10 Bending moment on the hose section

图11 油管截面压力Fig.11 Pressure on the hose section

综合3.1节的讨论结果，甩鞭现象会导致作用在受油管截面的最大拉压力、最大剪切力和最大弯矩出现显著增大，约束力的变化频率和变化幅度也会显著的提高。此外，甩鞭现象还会使得输油软管受力状态发生较大的改变，在输油管软管靠近锥套的部分受力增加尤为明显。因此，需要重点考察加油机与受油机间相对运动而诱发的甩鞭现象。

3.2 输油软管长度和飞行速度不确定

3.2节分析在给定高度下输油软管长度和飞行速度为不确定量时，受油管指定截面的受力期望曲线和最大概率分布范围。输油软管长度为在区间[24, 27] m中均匀分布的随机变量，加油机飞行速度同样服从均匀分布，不同高度下，加油机飞行速度区间如表3所示。结合第2节介绍的基于多项式混沌的不确定性分析理论，取多项式混沌的最大展开阶数为两阶，利用2.2节中的随机响应面法确定多项式混沌的展开系数。系统中的其他参数如表2所示。分析结果如图12 所示。

表3 不同高度下加油机平飞速度Table 3 Horizontal speed of the tanker at different altitudes

从图12中的不确定性分析结果来看，不同高度下，受油管截面所受到的压力、剪力和弯矩随时间变化走势基本相同，而且大小相差不大。这是因为在不同高度下，改变的量为空气密度、重力加速度及飞行速度，尽管在高空的飞行速度更高，但此时空气密度和重力加速度都有减小，因此在不同高度下，油管截面的受力相差不大。油管截面受到的压力上确界最大概率为6 880 N，剪力上确界最大概率为1 325 N，弯矩上确界最大概率为338 N·m。

图12 受油管截面受力的不确定分析(无甩鞭现象)Fig.12 Uncertainty analysis of force on the probe section(without HWP)

3.3 输油软管长度和对接速度不确定

从3.1节中的分析得知，甩鞭现象会使得受油管截面的受力大大增加。甩鞭现象的产生主要是因为受油机相对加油机的运动导致了输油软管出现屈曲变形和高频振动。本节中以受油机相对加油的运动速度大小和油管长度为系统输入随机变量，并假定相对运动速度在区间[0, 3] m/s内均匀分布，油管长度在区间[24, 27] m内均匀分布。在500 m，6 000 m和9 000 m高度下按表3中的最大飞行速度对受油管截面受力进行不确定性分析。系统其他参数按照表2输入，油管截面的受到的约束力如图13所示。对比图13与图12，出现甩鞭现象后，油管截面的受力大幅增加。截面受到的压力上确界最大概率为10 770 N，剪力上确界最大概率为4 479 N，弯矩上确界最大概率为1 474 N·m。相比于不存在相对运动的对接过程，受油管在特定截面处的最大压力、剪力和弯矩的期望值分别提高了50%、272%和772%，可见，加油机与受油机间的相对运动是相关部件强度设计需要考虑的重要因素。

图13 油管截面受力的不确定分析(存在甩鞭现象)Fig.13 Uncertainty analysis of force on the probe section (with HWP)

4 结 论

1) 采用绝点节点坐标法和ALE描述方式建立了输油软管的动力学模型，采用刚体假设建立锥套模型，叠加直匀流和Hallock-Burnham尾涡模型建立简化流场模型，采用试验公式拟合油管受到的气动力，最终建立了空中加油系统刚-柔-液耦合的多体动力学模型，该模型可用于计算空中加油对接约束力，并能够预测甩鞭现象。相比于集中参数模型，本文采用非线性有限元技术建立的输油软管模型能更加真实地反映柔性油管的动力学特性及燃油流动所对系统动力学的影响，并能得到输油软管上连续分布的受力状态。

2) 仿真发现：相比于正常对接过程，出现甩鞭现象时，受油管截面受到的压力、剪力和弯矩都将大幅增大；输油软管的受力状态将会发生较大的改变，轴向变形由受拉转变为主要受压，截面弯矩将会大幅增大，同时还会出现较高频率的振动。

3) 多项式混沌方法可用于输入参数不确定情况下对接约束力的分析计算，能够以较少的计算量给出对接约束力的期望值和标准差，估计出最大概率意义下的约束力的上界。