风沙两相流数值模拟研究进展
王萍,郑晓静
兰州大学 湍流-颗粒研究中心 西部灾害与环境力学教育部重点实验室,兰州 730000
风沙运动是沙质地表上的沙尘颗粒在风力作用下以地表蠕移、近地表跃移、远离地表悬移而进行输运的一种自然现象。常见的沙质地表有占全球陆地面积1/3的沙漠和荒漠化地区[1],海边的沙滩和裸露的农田和建筑工地等。沙尘颗粒的输运,在近地表1~2 m以下的高度范围内以粒径大于约100 μm的颗粒跃移运动为主,其输沙率占总输沙率的75%以上[2],是风沙运动的主导;在离地表1~2 m乃至数百米以上高度范围内以粒径小于100 μm甚至数μm(如PM10)的颗粒悬移运动为主,其输沙率不及跃移风沙流,仅占总数不到5%[2],但这些沙尘粒子可以长期漂浮于对流层上部和平流层并远距离输运。当高超声速飞行器再入行星大气层时,这些粒子可能与飞行器高速撞击,使其表面遭到破坏,甚至与飞行器头部激波层相互干扰,导致飞行器表面加热率改变[3]。跃移风沙流往往导致土壤风蚀、农林作物受损、交通道路掩埋等危害,而风沙运动的极端情形沙尘暴则往往导致大范围空气质量下降、无线通讯信号中断、汽车火车翻车甚至人员伤亡。例如,2010年4月24—25日在甘肃发生的沙尘暴共造成甘肃19个县约132.56万人受灾;农作物受灾面积达20.68万公顷。沙尘暴不仅在中国西北地区频发,在非洲的撒哈拉地区、沙特阿拉伯首都利雅得、澳大利亚悉尼、美国亚利桑那州凤凰城等也时有发生,而且在地外行星如火星上也经常发生。风沙运动引发的风沙流和沙尘暴已经成为影响人类经济社会发展的一个重要环境问题,防治风沙灾害被联合国《2030年可持续发展议程》确立为17个可持续发展目标之一[4],也被列入《全国重要生态系统保护和修复重大工程总体规划(2021—2035年)》[5]。
风沙运动这种自然现象在本质上是大气边界层可蚀地表上摩阻雷诺数高达106~107的气-固两相流。大气边界层特别是近地表湍流的强非线性、巨量的沙尘颗粒大小和形状以及起动条件的随机性、可蚀地表上颗粒冲击床面和碰撞后的反弹和溅起的复杂性、颗粒运动与湍流相互作用的耦合效应以及沙尘颗粒带电形成风沙电场[6]与湍流流场的多场耦合、由瞬间启动和碰撞的微米大小的颗粒导致的在数秒钟即可达到饱和的数米高度范围的风沙流、进而造就长达数百年形成演化出的数千平方公里范围沙漠的这种时空多尺度和跨尺度性等,使得风沙运动具有当前许多学科面临的多重非线性、多场耦合性、多尺度交织的共性,其定量模拟和准确预测十分困难。著名流体力学家Balachandar在其综述文章中指出:“湍流和多相流是流体力学中最具挑战性的2个问题,湍流所固有的随机性由于颗粒的随机分布而变得更为复杂。颗粒相的存在使得多相流的试验观测和数值模拟比单相流复杂得多……即使是在稀疏扩散相的条件下,当两者联合起来也会成为更加难以对付的挑战”[7]。而《Science》列出的125个未解决的重要科学问题[8]中唯一一个直接与力学相关的问题就是“能否发展湍流动力学与颗粒运动学的统一模型”。
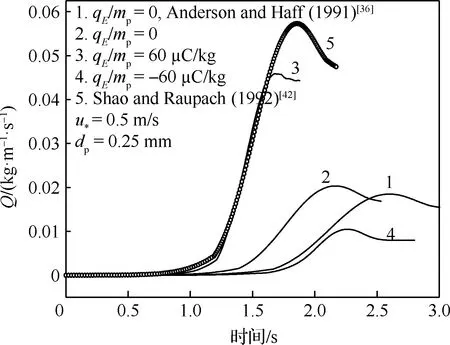
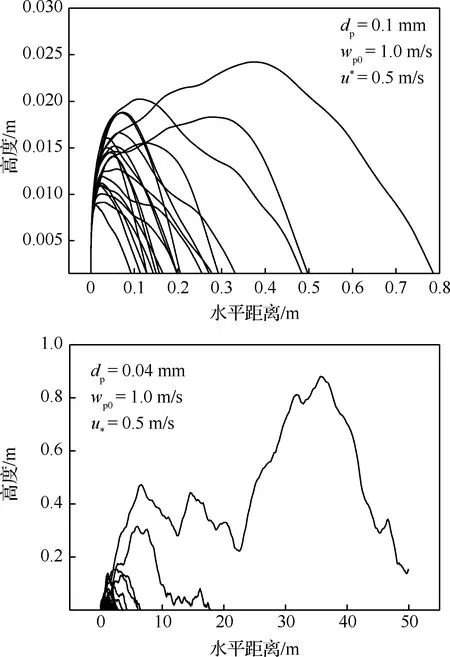
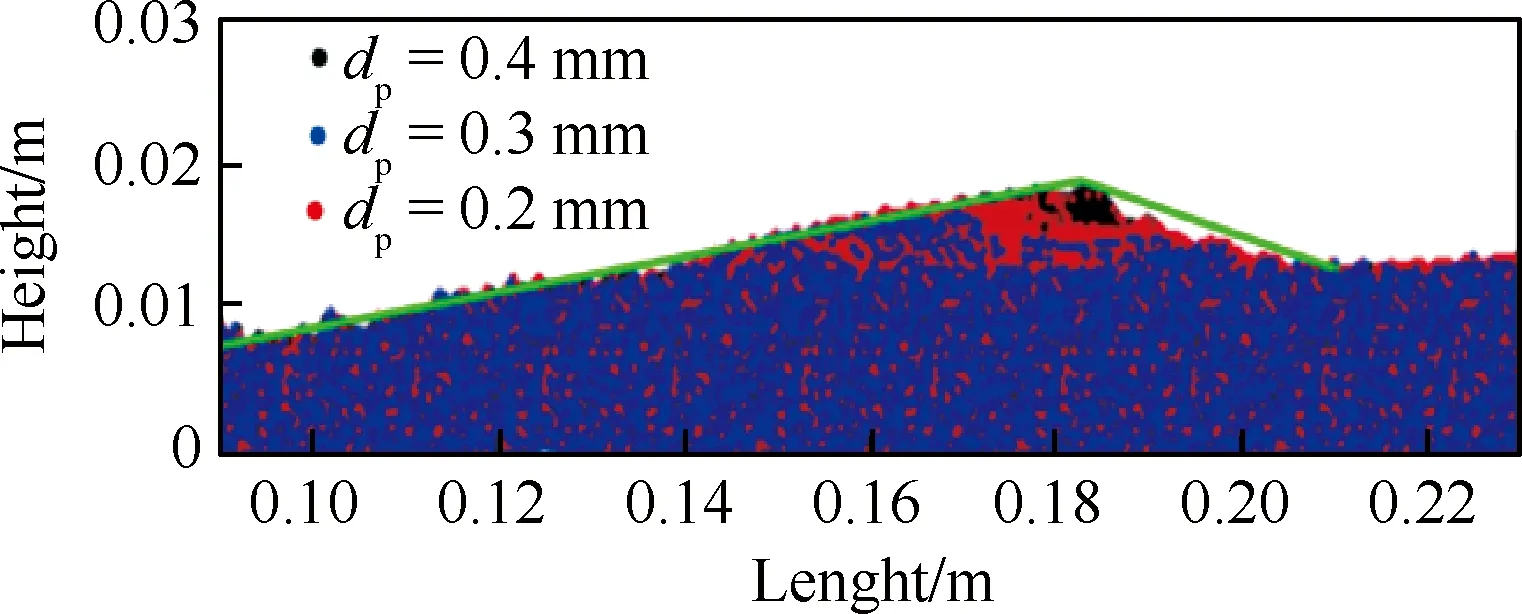
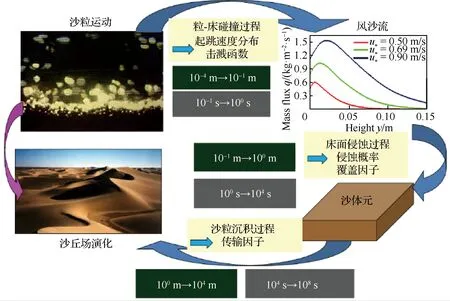
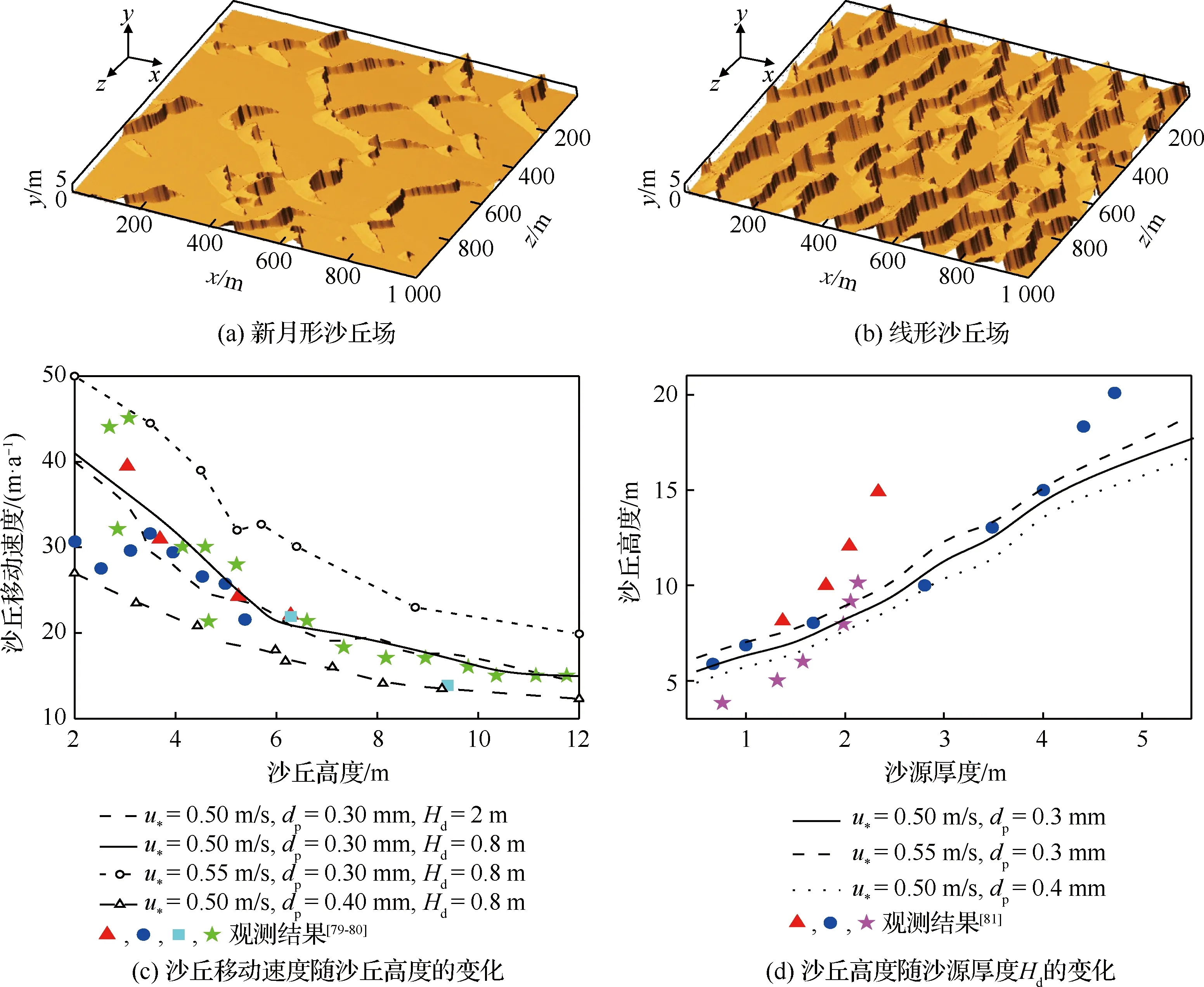
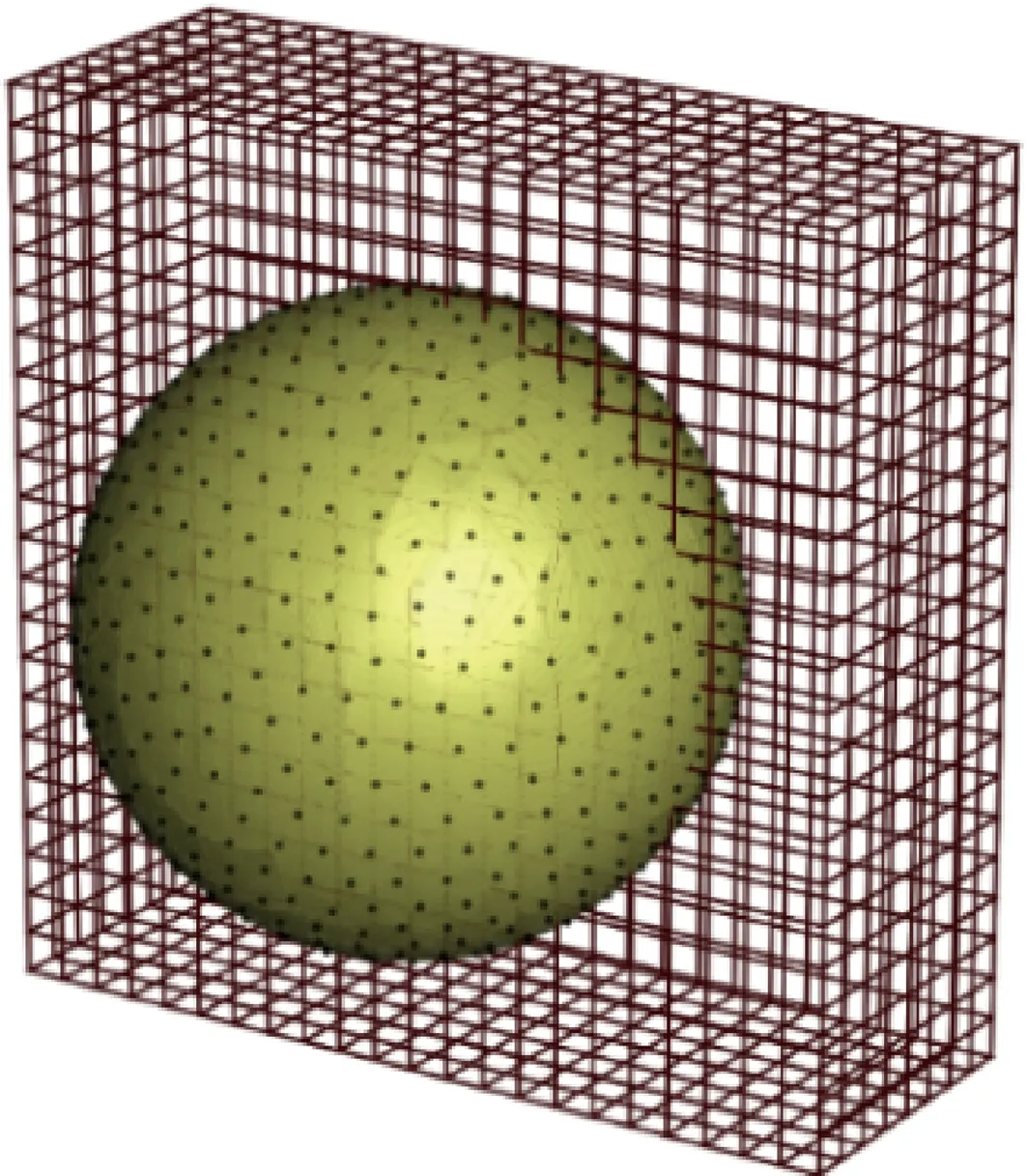
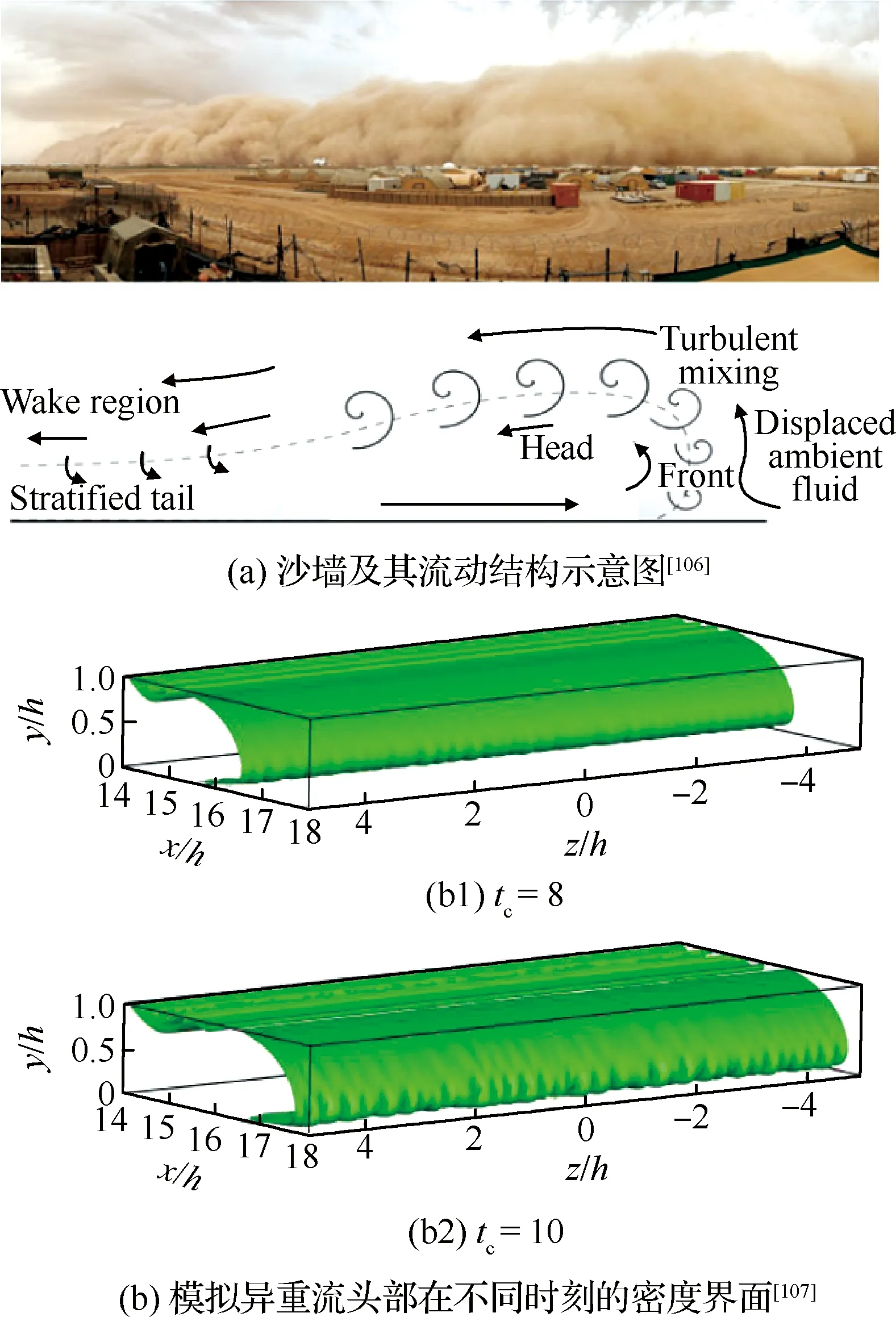
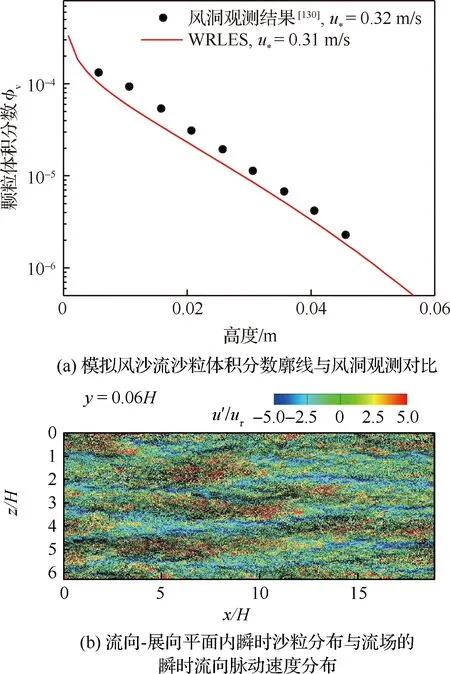
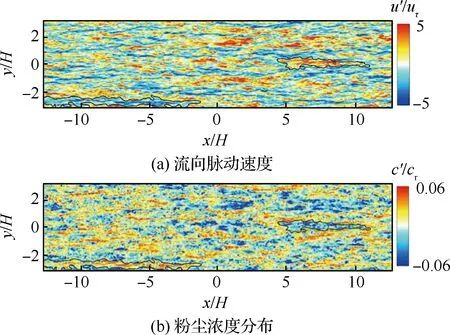
风沙运动的科学研究始于20世纪40年代,早期以野外观测和风洞(包括固定式风洞和便携式风洞)试验为主要研究手段。这一时期最为重要的著作是英国工程师Bagnold所著的《The physics of blown sand and desert dunes》[2]。他运用流体力学当时的最新研究成果,即普朗特边界层理论,结合野外考察与风洞试验,为风沙物理学奠定了基于试验观测的经验性定量分析的基础。在他的研究中,近地表的跃移风沙流被划分为可蚀床面的沙粒在风场作用下的流体起动,起跃沙粒在风场作用下的跃移运动,跃移沙粒与可蚀床面的冲击碰撞、反弹及床面沙粒的溅起,跃移沙粒对风场的反作用这4个子过程。但他只是对这几个过程进行了定性的描述。20世纪60~80年代,由于人类对太空探测的兴趣,研究者们开始了风成地貌与风沙运动的定量模拟以对无法直接观测的地外行星,如火星、金星上的风沙运动进行预测。这一时期的开创性工作是Owen[9]发表的《Saltation of uniform grains in air》。他通过假定所有从床面起跳的沙粒运动服从同一简单形状的轨道,在欧拉-拉格朗日框架下建立了考虑重力和气流对沙粒拖曳力的沙粒运动方程、考虑沙粒反作用力与剪应力梯度平衡的流体速度方程,理论推导出受沙粒运动影响的流场速度分布、跃移风沙流的输沙率等。模型中,Owen通过假设拖曳力正比于沙粒流体相对速度VR,将二维沙粒运动方程组解耦为2个二阶常系数非齐次微分方程,因而获得沙粒速度的理论解。但这一假设仅在沙粒雷诺数Rep(Rep=VRdp/ν, 其中dp为沙粒粒径,ν为空气运动黏度)小于1、阻力位于Stokes区的情况下近似成立,而实际跃移沙粒的雷诺数应为1 20世纪80年代以后,随着对两相流问题研究的不断深入,逐渐发展起风沙两相流的三流体模型[13](即将向上和向下运动的沙粒用2种拟流体表征)和悬移粉尘平衡模型[12](即粉尘的沉降与扩散平衡)等。与此同时,一些学者,如Ungar 和Haff[14]以及Werner[15],逐渐开始在风沙流的模拟时考虑跃移风沙流的第3个子过程,即跃移沙粒与可蚀床面冲击碰撞后的反弹/溅起,同时更加完整地考虑跃移风沙流的第4个子过程,即跃移颗粒对风场的反作用。这方面的代表性工作为Anderson 和Haff[16]于1988年发表的《Simulation of eolian saltation》。他们把由试验测得的跃移颗粒起跳初速度分布和由单颗颗粒单次冲击可蚀床面的冲击速度与溅起颗粒数/速度的拟合关系(击溅函数)作为颗粒运动的初值条件,并通过颗粒对流场的反作用将颗粒运动方程与流场方程耦合。不仅如此,颗粒运动方程中表征拖曳力的风场速度也不再仅由平均速度廓线确定,而是由雷诺平均Navier-Stokes(RANS)方程求解后代入。通过联立求解颗粒运动方程和流场方程,进而实现对跃移风沙流形成和演化直至饱和的全过程的数值模拟。由此把20世纪70年代的流体力学在两相流理论和Navier-Stokes方程的RANS求解用于风沙流的模拟,为风沙物理学奠定了基于数值模拟的统计性定量分析的基础。然而,基于RANS仅能模拟湍流平均风场及其与颗粒的相互作用,所得到的输沙率往往随时间、空间不变,这与实际观测发现的输沙存在显著时空变化[17-20]不符,而这种时空变化被认为与湍流结构[21-23],尤其是外区的大尺度/超大尺度运动(Large Scale Motions/Very Large Scale Motions, LSMs/VLSMs)[24-26]密切相关[27-29]。同时,风洞试验与野外观测均发现了低于风沙物理学中所给出的理论起动风速条件下的输沙[30-32],意味着湍流的近壁结构对起沙具有重要作用[33-34]。因此,在对风沙两相流预测中仅用RANS描述风场是远远不够的,需要更多考虑湍流脉动与结构影响。 本文将回顾风沙运动数值模拟近30年的研究进展。注意到,尽管两相流数值模拟方法大致可分类为欧拉-欧拉、欧拉-拉格朗日、拉格朗日-拉格朗日3类,但已有风沙运动数值模拟仍以前2类为主,因此本综述也仅侧重前二者。在第1节将介绍基于RANS的风沙两相流数值模拟,并作为应用,给出风成地貌沙波纹和沙丘场形成演化过程的模拟。第2节介绍壁解析大涡模拟(Wall Resolved Large Eddy Simulation,WRLES)方法在风沙两相流模拟研究中应用的现状及前景。第3节介绍基于壁模型大涡模拟(Wall Modeled Large Eddy Simulation,WMLES)的风沙运动数值模拟研究,第4节给出风沙运动数值模拟未来发展的趋势以及值得进一步研究的若干关键问题。 RANS方法由于仅求解湍流平均运动方程,因此,能够以较小的计算量得到工程上所关心的平均统计特性。假定大气表面层气流(Atmospheric Surface Layer,ASL)为不可压缩流动,其所满足的雷诺平均动量方程和连续性方程为 (1) (2) 式中:xi为坐标,i=1,2,3分别代表流向x、垂向y、展向z;Ui为流体平均速度,流向、垂向、展向速度分量分别记为U、V、W;t为时间;p为压力;ρ、μ分别为空气的密度和动力黏度;Fi为颗粒对不同高度上流体的反作用力;τij=μt·(∂Ui/∂xj+∂Uj/∂xi)为雷诺应力,μt为涡黏系数。风沙运动RANS模拟中一般采用混合长度模型和k-ε模型等进行方程封闭。沙粒运动采用拉格朗日点力模型计算时,当考虑拖曳力FDi、重力FG和电场力FE时,所满足的运动方程为 (3) 式中:upi为沙粒速度,流向、垂向、展向速度分量分别记为up、vp、wp;ρp、mp分别为沙粒的密度和质量;g为重力加速度;Ei为电场强度;qE为沙粒所带电荷量;CD为拖曳力系数;u@i为沙粒所在位置处流场速度;δi2为Kronecker记号。|u@p-up|为流场与沙粒速度矢量差的模。需要指出的是:附加质量力、Basset力、Saffman升力、沙粒旋转产生的Magnus力以及颗粒空中碰撞产生的碰撞力等也对沙粒运动以及输沙率等有定量影响,具体可参见Zheng的专著《Mechanics of wind-blown sand movement》[1]。 Ungar和Haff[14]运用混合长度理论封闭无限大平坦沙床表面的一维气流动量方程,首先建立了风场-沙粒相互耦合的稳态风沙流数学模型,即将式(1)简化为 (4) 式中:Fx为颗粒对流体反作用力的流向分量;κ为von Kármán常数。假定所有从床面起跳的沙颗粒具有相同的起跳速度和弹道形式的轨迹,其轨迹方程仅考虑拖曳力和重力。沙颗粒在一次飞行过程中2次经过同一高度y,则其对单位体积风的阻力可表示为 (5) 式中:N1为单位时间内从单位面积床面上起跳的沙粒数;vp↑及vp↓分别为上升沙粒与下降沙粒在高度y处的垂向速度分量;FDx↑及FDx↓分别为相应沙粒上所受拖曳力FDi的水平分量。在此基础上,Ungar和Haff[14]提出了一个简化的δ函数形式的击溅模型,描述沙粒以速度Vimp冲击床面后,以V0起跳的沙粒数: (6) (7) 以风速U(y)廓线和目标剪切风速u*作为收敛条件,通过双重迭代可获得风沙流稳定状态。这一方法也被Zheng等[35]进一步应用,揭示出输沙率沿高度的分层现象,即:输沙量在贴近沙床附近处随高度线性增加、达到极值进入饱和层、然后沿高度按负指数规律衰减。这为“沙割”现象的解释提供了理论依据。需要指出的是,此类方法只通过颗粒-流场的耦合计算获得稳态自平衡的风沙流模拟结果,无法再现风沙流的形成发展过程。 Anderson和Haff[16,36]率先完整实现了包含风沙运动全部4个子过程的、从沙粒起动到风沙流自平衡状态的时间发展全过程的模拟,随后McEwan和Willetts[37-38]又对风沙流的这一发展过程进行了更为细致的模拟。在他们的模拟中,流体起动颗粒数Na被假设为正比于流体剪切应力与床面颗粒起动的临界剪切应力之差 Na=Ca(τw-τc) (8) 式中:τw为床面流体切应力;τc为风力直接吹起沙粒时的临界应力,可由理论分析结合风洞试验得到;Ca为比例常数。击溅过程则通过离散单元法(Discrete Element Method,DEM)模拟或采用试验观测给定的经验函数[1,36,39-40]来计算。Anderson和Haff[36]基于其二维DEM(沙粒碰撞简化为2个均质圆盘)模拟结果提出 Pr=0.95(1-exp(-2.0Vimp)) (9) (10) 图1 单宽输沙率随时间发展过程[1]Fig.1 Time evolution of sand transport rate[1] 风沙流/沙尘暴中由于颗粒间、颗粒与床面间的接触摩擦等会导致颗粒带电并形成风沙电场,其强度可到数十至上百kV/m[47-49]。带电沙粒所受静电力的大小与沙粒自身的重力相当,因而风沙电场直接影响沙粒运动。同时风沙电场大小与沙粒带电量以及空中沙粒数密切相关。因此,由沙粒带电所产生的风沙电场与沙粒运动和风场之间也存在着相互耦合作用。在均匀稳态风沙流中只存在垂向电场,Zheng等[50]结合风洞试验研究所获得的沙粒带电和风沙电场规律,建立了考虑风-沙-电多场耦合的风沙流模型,如图2[1]所示。根据试验观测,假定空中沙粒在平均意义下带负电荷,沙床表面沙粒即蠕移沙粒在平均意义上带正电荷,空中某高度y处的垂向电场E(y)视为由晴天大气电场E0、空中带负电荷的沙粒在点y处所产生的电场Es、沙床表面带正电荷的沙粒在点y处所产生的电场Ec这3部分组成: 图2 点电荷产生电场示意图[1]Fig.2 Schematic diagram of electric field produced by a point charge[1] E(y)=E0(y)+Es(y)+Ec(y)=-0.1+ (11) 式中:N为单位体积内空中运动的沙粒数,在稳态风沙流中只随高度变化;ε0为空气介电常数;cq=qE/mp为荷质比,即单位质量沙粒所带电荷量,试验观测给出其均值约在±O(100 μC/kg)范围内[47-48];a和b为电荷影响空间范围,实际计算发现,a和b的取值大于100 m后电场计算结果不受影响。数值模拟结果表明,考虑垂向风沙电场,带正电(荷质比为60 μC/kg)的颗粒运动轨迹的长度比不带电的增加了163%,带负电(荷质比为-60 μC/kg)的却减小了57%[47]。而当颗粒带正电(荷质比为60 μC/kg)时,模拟的多场耦合风沙流随时间演化过程能够与风洞试验观测结果更吻合(见图1)。但是式(11)中沙粒平均带电量(或荷质比)为常数,不能反映沙粒碰撞带电物理过程。为此,Kok和Renno[51]基于硬球模型和接触势差带电机制,模拟沙粒碰撞带电以及多场耦合风沙流。该模型能够解释“大颗粒带正电小颗粒带负电”现象,但其中涉及的物理参数为经验参数,需试验测定。Hu等[52]进一步采用软球模型计算碰撞颗粒间电荷转移,不同于硬球模型不考虑碰撞过程中的细节,软球模型能够反映颗粒尺寸和碰撞速度对于单次碰撞带电量的影响。带有电量qEi、qEj的2个颗粒碰撞后,各自的带电量分别为 (12) 其中:ρH,0为高能态束缚空穴面密度;e为单位元电荷;CE为常参数;Si、Sj为碰撞接触面积。将该模型应用至风沙流中可以更好地模拟荷质比随着风速的变化规律。此外还发现,颗粒荷质比服从正态分布且其均值随着空中碰撞效应的增强而逐渐趋向于0。 最近,一些学者结合RANS流场还发展了基于二维DEM的风沙流模拟方法,直接在颗粒尺度上求解沙粒-床面碰撞过程。如Carneiro等[53]采用此方法模拟了500颗具有高斯分布粒径的球形沙粒床面上的风沙流,发现输沙率在低风速下存在亚稳定状态。Durán等[54]数值模拟15 000颗粒沙粒组成的床面上的沙粒运动,分析不同密度比(风沙与水沙)条件下输沙规律的异同;在Durán等[54]仅包含重力、浮力和拖曳力的颗粒运动模型基础上,Pähtz和Durán[55-56]进一步在模拟中考虑了附加质量力,分析床面颗粒平均速度及其与跃移层平均颗粒速度关系、风沙流起动与输沙停止的临界风速条件、流体颗粒密度比以及Galileo数的影响等。虽然DEM模拟可以避免采用经验击溅函数带来的误差,但由于计算量限制,已有的数值模拟工作或者计算颗粒数较少、或者计算域很小,远未达到实际风沙运动的颗粒数量和空间尺度范围。 以上基于RANS流场的稳态风沙流数值模拟对于理解风沙运动起到了极大的促进作用,但RANS仅模拟平均流动,平均掉了所有的湍流脉动。事实上,由于颗粒所受拖曳力正比于其迎风横截面积,粒径越小、受力越小、轨迹越低,因此即便粒径相当小的悬浮颗粒(<10~20 μm),在平均流场中采用点力方法模拟,其飞行高度也仅限于离地表约1~2 m以下,与沙尘天气中沙尘颗粒能够被传输至对流层上部进行远距离输运的实际不符。在RANS模拟中计及风场的湍流脉动效应,目前主要有2类途径,一种是在稳态风沙运动模型的基础上直接施以非定常风速,如Spies等[57]、作者团队[58]通过在计算域上边界施加正弦变化的周期性风速脉动,模拟非平稳风沙流,获得风沙流输沙率Q(t)随来流风场参数(周期与幅值)的变化规律,如图3[58]所示,其发现脉动风速增加风沙流输沙率,平均风速越小,增加越显著。Zhang等[59]进一步考虑颗粒带电的非稳态风沙流模拟发现,除了垂向电场之外,由于输沙率在水平方向的不均匀性,风沙流发展过程中还会形成水平方向的风沙电场。另一种途径是借鉴描述重颗粒扩散的拉格朗日随机模型,通过在平均速度廓线上叠加采用郎之万方程描述的流场速度脉动[60-62]或直接对颗粒运动采用修正郎之万方程[63]描述的方法求解颗粒轨迹。以前者为例,该方法即在式(3)中对u@i的脉动部分u′@i采用以下表达式计算: 图3 在正弦变化风场中的输沙率Q(t)演化[58]Fig.3 Development of sand transport rate Q(t) in sinusoidal wind variations [58] (13) 图4 典型沙尘颗粒随机运动轨迹[67]Fig.4 Typical stochastic trajectories of sand/dust particles[67] 对于小粒径悬移粉尘的远距离、大尺度输运的计算,除采用上述拉格朗日随机模型方法以外,还可以采用欧拉-欧拉模型求解。实际上,现有的沙尘数值预报模式[71-75]中多采用欧拉-欧拉模型计算沙尘浓度分布、提供预报数据。这主要是因为如果采用拉格朗日随机模型跟踪每一颗粒的运动轨迹,为获得统计可靠的结果,需要跟踪的颗粒数量巨大,使该方法难以在数值预报中实际应用。在欧拉-欧拉模拟中,沙尘浓度c服从有源/汇项的、对流-扩散类型的守恒方程[76],即 (14) 风成地貌如沙波纹、沙丘和沙丘场,目前尚未见按连续介质理论成功模拟的例子。这主要是因为涉及沙粒尺度(10-4m)、风沙流尺度(10-1~100m)、沙丘和沙丘场尺度(100~104m)至少3个长度尺度,以及沙粒起跳和跃移的时间尺度(10-2~10-1s)、风沙流形成和持续的时间尺度(100~103s)、沙丘和沙丘场形成和发展的时间尺度(104~108s)至少3个时间尺度。同时,在不同时空尺度上的现象和行为有着不同的结构层次和不同的演化速率以及不同的物理机制,因而很难建立涉及地表侵蚀、风沙流沉积等典型过程的本构模型。结合沙粒的散体性和基于离散建模的计算机模拟风成地貌的方法(如元胞自动机),虽然在不同程度上也能模拟出沙波纹和沙丘, 但由于均需要赋以一些人为的规则而使得模拟结果与实际风成地貌不符。基于RANS模拟给出的沙粒冲击地表速度和输沙率以及平均跃移长度等统计量,Zheng等[77]提出的离散粒子追踪法(Discrete Particle Tracing Method, DPTM) 对风成沙波纹的发展过程实现了计算机模拟。该方法同时考虑了与真实沙波纹形成相关的3个主要因素, 即不同粒径的众多沙粒在沙床上方所形成的风沙流、风沙流中沙粒对沙床的碰撞以及碰撞后沙粒的反弹或溅起、沙粒在床面上方的跃移和在床面的蠕移。其中,风沙流模拟给出的颗粒冲击地表作为由混合粒径颗粒组成的离散床面模拟系统的能量输入。其模拟结果(见图5[1])不仅再现了沙波纹从平坦沙床出现—长大—分叉—合并—饱和的全过程,而且模拟得到的沙波纹尺寸和移动速度、沙波纹的自修复过程、沙波纹顶部沙粒粒径大底部粒径小的倒粒序结构、以及沙波纹出现和消失的临界摩阻风速等特性与观测结果符合。 图5 离散粒子追踪法模拟得到的混合粒径沙波纹(摩阻风速为0.5 m/s)[1]Fig.5 Sand ripple in varied-sized case simulated by DPTM (friction wind velocity is 0.5 m/s)[1] 如果说对于沙波纹的形成演化过程可以通过对一颗颗沙粒的运动模拟得到,那么对于沙丘与沙丘场,其计算量显然是不允许的。为此,仍然基于对风沙流的RANS模拟,Zheng等[78]提出了一种类似于三级跳远的“三级跳”方法(见图6[1]),即:耦合尺度沙丘场模型——基于近地表输沙的典型离散模型。该模型不仅需要击溅函数和沙粒起跳速度分布这些涉及沙粒近地表运动的已有统计量,而且其还推导出床面的侵蚀因子和覆盖因子以及沙粒输运的传输因子这3个新的统计量。具体的推导可见文献[1]。该模型成功实现了从一颗颗沙粒运动到风沙流再到“沙体元”进而到数百平方公里甚至更大范围的沙丘场从任意初始状况(包括平坦情况)形成和发展的长达数十年或数百年演化过程的定量模拟,实现这一具有时空尺度在108~109量级的跨越。其模拟结果除了定性上与野外观测结果一致外,如沙漠边缘的新月形沙丘场(见图7(a))和沙漠腹地的线形沙丘场(见图7(b)),在定量上,如沙丘运动速度随高度的变化(见图7(c)[79-80])和沙丘高度随沙源厚度Hd的变化(见图7(d)[81])也与野外观测结果吻合。在此基础上,Zheng等实现了对沙漠边缘扩展速度的理论预测,使得沙漠扩展速度从原来的“后知后觉”到提前获知;其还给出为遏制扩展速度所用的固沙草方格的优化铺设方案,使得固沙成本可降低2/3。 图6 风成沙丘场演化过程定量模拟示意图[1]Fig.6 Schematic diagram in quantitatively simulating evolution process of aeolian dune field[1] 图7 模拟沙丘场及其统计结果[1,78]Fig.7 Simulated sand dunes and their statistics[1,78] 如前所述,湍流结构对风沙运动中沙尘颗粒的起动、输运均有重要影响,因此,理论上,湍流直接数值模拟(Direct Numerical Simulation, DNS)更适于近地表风沙运动研究。事实上,基于DNS与点力方法的数值模拟已经广泛应用于均匀各向同性湍流、自由剪切湍流、槽道、管道、湍流发展边界层中的颗粒两相流动模拟[82-95]。在相对简单的固壁条件下,揭示了颗粒在壁湍流边界层中的聚集特性、颗粒对湍流的调制规律。如Zhao 等[88-89]发现球形颗粒与槽道湍流相互作用会增加动能耗散,同时颗粒运动会使流场湍动能在空间再分配,颗粒湍流相互作用还抑制颗粒的转动行为;Wang和Richter[92]发现惯性颗粒在外区倾向于分布在湍流高速区,同时颗粒增强湍流LSMs/VLSMs,且这种增强随颗粒Stokes 数(颗粒惯性时间尺度τpar与湍流时间尺度τtul之比)非单调变化,颗粒在湍流内、外区都存在与当地湍流结构相关的非均匀分布。对于尺寸大于湍流最小尺度(Kolmogorov尺度)的颗粒,不能再将颗粒视作一点,颗粒需要被精细分辨并考虑颗粒表面的无滑移边界条件[96-98],采用浸没边界法计算颗粒与湍流间的相互作用,此即全分辨模拟,如图8[99]所示。最近,湍流DNS模拟结合颗粒全分辨模拟也被应用于分析可蚀地表上的颗粒运动及其与湍流的相互作用[100-104],如Ji等[100-101]采用全分辨方法与湍流DNS模拟可蚀床面上跃移颗粒两相流,分析颗粒与湍流的相互作用,发现湍流下扫与颗粒的流体溅起密切相关,而颗粒运动将破坏近床面湍流结构。Vowinckel等[102]采用类似的方法研究全分辨可蚀床面上的颗粒湍流相互作用,不仅发现湍流被增强,还发现可蚀性导致高质量分数下床面形成长达12倍计算域高度的丘状颗粒分布、低质量分数下形成颗粒聚集的现象等。作者所在团队也开展了可蚀地表大颗粒(~500 μm)与湍流相互作用的全分辨直接数值模拟研究[105],全分辨球体瞬时分布与流场速度分布如图9[105]所示(该算例模拟总颗粒数为7 200);利用DEM解析颗粒与颗粒、颗粒与床面之间的碰撞,基于该模拟结果识别流体起动、反弹、溅起事件,分析了颗粒速度分布。在此基础上,针对全分辨直接数值模拟的大规模并行计算,提出了按颗粒数划分的并行算法,并对颗粒信息存储进行了优化,使得可计算颗粒数能达到百万量级。 图8 球形全分辨颗粒模拟的欧拉网格点和拉格朗日网格点分布[99]Fig.8 Distribution of Eulerian grid points and Lagrangian grid points over a fully resolved sphere [99] 图9 全分辨直接数值模拟颗粒分布示意图[105]Fig.9 Schematic diagram of fully resolved particle distribution in DNS[105] 图10 沙尘暴沙墙结构与异重流模拟Fig.10 Sand wall and numerical simulation based on gravity current model 壁湍流的DNS,即便单相流动,目前所能达到的最高摩阻雷诺数Reτ(Reτ=uτH/ν,H为边界层厚度,uτ为湍流壁面摩擦速度)也一直在O(103)徘徊[108-111]。而大部分两相流数值模拟,考虑到颗粒带来的额外计算量,Reτ则多限于O(102)。目前基于点力方法的最高雷诺数可能是Bernardini[90]的Reτ=1 000的单向耦合槽道两相流模拟、Wang 和 Richter[92]的Reτ=950惯性颗粒双向耦合两相流模拟、Jie等[112]Reτ=1 000 的非球形颗粒两相流模拟。而对于颗粒全分辨模拟,由于要分辨每个颗粒周围的流场,计算量进一步急剧增大,如Kidanemariam 和 Uhlmann[103]中颗粒数105万、雷诺数Reτ=293的单个算例需要计算500万核时,这也导致目前全分辨颗粒两相流的湍流最高雷诺数仅为Reτ=647[100],远低于大气风沙两相流起沙雷诺数(野外Reτ~105,风洞Reτ>2 000~3 000)。 湍流大涡模拟直接求解滤波尺度以上的“大涡”,而对亚格子尺度“小涡”建立模型(即亚格子模型),从而能够以更小的计算量得到接近DNS 的湍流脉动与结构信息,因而被认为是最具潜力的湍流模拟工具[113]。如果颗粒尺寸小于LES最小可解尺度或颗粒密度远大于流体,点力大涡模拟是实现高雷诺数湍流两相流数值模拟最具吸引力的方法[114]。大涡模拟的控制方程为滤波后的Navier Stokes方程和连续性方程。 (15) (16) 图11 采用欧拉-拉格朗日方法模拟湍流颗粒流的概念分类[115]Fig.11 Conceptual classification of Eulerian-Lagrangian modelling approaches for simulation of particle-laden flows [115] 在较低的雷诺数下,即便不考虑亚格子湍流对颗粒运动影响,基于WRLES流场的两相流数值模拟也被证明可以获得与基于DNS流场模拟一致的结果,且亚格子模型(Smagorinsky模型和动力Smagorinsky模型)对模拟结果影响较小[117-118],因此,已逐步被用于分析颗粒的沉积和扩散以及颗粒对湍流的调制[119-127]等研究。值得一提的是,最近WRLES结合DEM方法对可蚀床面上悬浮两相流数值模拟的湍流雷诺数与模拟的颗粒总数相比DNS都得到了大幅提升。比如在Schmeeckle[124]的研究中,最大摩阻雷诺数约为3 470,模拟最大颗粒总数为33万,而Capecelatro和Desjardins[123]在圆管泥沙流动的WRLES结合DEM模拟中雷诺数约为2 000,颗粒数达到了1 600万。对于风沙运动,本文作者团队采用WRLES结合点力模型对近地表跃移风沙两相流进行了较为精确的数值模拟[128],雷诺数最高达Reτ=4 200,亚格子湍流对可解尺度湍流的贡献采用动力Smagorinsky模型计算,同时忽略了颗粒与亚格子湍流之间的相互作用,即颗粒与湍流的相互作用只发生在可解尺度上。采用三维击溅函数(将式(9)扩展为三维[129])作为沙粒运动下边界条件,同时考虑沙粒流场双向耦合,单时间步跟踪总沙粒数达5 000万。数值模拟统计量与风洞试验结果吻合,且再现了沙粒在风洞尺度上的大尺度分布(见图12)[128,130],也这也是目前唯一采用WRLES精细模拟风沙运动的工作。 图12 风沙运动WRLES模拟所给出的沙粒体积分数廓线和瞬时分布[128]Fig.12 Volume fraction profiles and instantaneous distribution of sand particles obtained by WRLES simulation[128] 壁湍流边界层含能涡尺度随距离壁面高度的增加而迅速减小。WRLES求解内层(边界层厚度的约10%以下)所需网格数几乎与DNS同一量级,且随Re的增加而增加。根据Piomelli[131]估算,当Re>106,超过99%的计算资源都用于求解内层,加之颗粒跟踪,因此湍流两相流模拟计算量仍是相当巨大的。例如本文作者团队Reτ=4 200 的风沙运动WRLES算例在OpenMP与Message Passing Interface(MPI)混合并行的情况下需要约40万核·时才能获得统计稳定的结果。这使WRLES难以应用至雷诺数高达105的野外实际风沙运动模拟。一种有效的湍流流场求解方案是采用壁模型大涡模拟,即:直接求解外区含能涡,内区对动量传输有贡献的涡由于网格非常粗糙而无法求解,因而从整个动力系统中移除,这将极大减小计算量。此时,需要将壁面应力与外区可解尺度速度相关联或在雷诺平均意义下对内区动量传输的影响进行求解以获得正确的速度廓线[131-132]。目前已经发展了许多的WMLES方法,大致上可分为混合RANS/LES模型和壁面应力模型2类。应用最为广泛的壁面应力模型是平衡率壁模型,通过假定速度廓线代数求解壁面应力或通过局部求解简化RANS方程估算壁面应力。Deardorff[133]和Schumann[134]最早应用了此类模型。此后,通过考虑浮力[135]、内区结构倾角[136]、外区湍流结构[137]、惯性项以及粗糙子层[138]、辐射[139]等影响不断修正以包含更为复杂的近壁物理和非平衡过程。 另一方面,在应用了壁模型的风沙运动WMLES工作中,其所采用的壁模型主要是通过假定速度廓线计算壁面应力,即假定近壁区存在当地可解尺度速度分布与当地剪应力之间的平衡关系,流向与展向壁面应力τw,yx和τw,yz的计算式为 (17) (18) (19) 其中:Δs是为考虑近壁结构倾角而引入的,以使得壁面应力与下游Δs处瞬时速度相关[136]。值得一提的是,文中采用了尺度依赖动力亚格子模型[144],在粗网格、低精度数值格式下再现高雷诺数湍流中的LSMs/VLSMs结构,不仅模拟出与野外实际观测一致的长度可达数十米的沙粒结构,还通过条件平均分析发现“Sand Streamers”出现在 LSMs/VLSMs 近壁面尾迹中,即“Sand Streamers”是 LSMs/VLSMs 在近壁面的“足迹”,见图13[143],由此揭示出 LSMs/VLSMs 对风沙两相流中颗粒运动的影响,证明在风沙运动中湍流结构的重要作用。 图13 风沙流中以高浓度c′>0条件平均的流向速度脉动u′[143]Fig.13 Conditionally averaged fluctuating streamwise velocity u′ for c′>0 in wind-blown sand flow[143] 以上采用壁模型进行风沙运动大涡模拟的工作中,所采用的壁模型本身也是不同的,虽然在风速较大时,冲击溅起过程主导近床面沙粒运动,使得不同壁模型对于风沙运动及其统计量的预测差别较小,但对于较低风速、流体起动占优的情况,床面附近速度与应力预测变得十分重要。Zheng等[145]对比了式(14)和Sidebottom等[146]提出的考虑外区LSMs/VLSMs对壁面应力调制的内外尺度相互作用(Inner-Outer Scale Interaction, IOSI)模型发现,在低风速下,尤其是剪切风速低于临界起动条件时,IOSI模型能预测更强的、与试验更符合的单宽输沙率,如图14[145]所示。据此,他们认为,外区湍流结构尺度(或边界层厚度)影响沙尘流体起动,这意味着野外条件下发生输沙的临界条件可能低于风洞,或者换句话说,同样剪切风速下,野外输沙率可能大于风洞的。 图14 低风速条件下计算无量纲单宽输沙率随无量纲剪切应力变化(根据Zheng等[145]改绘)Fig.14 Dimensionless transport rate as function of dimensionless shear stress at low wind speed according to Zheng et al. [145] 此外,即便在以上采用的壁模型两相流WMLES中,所使用的壁模型仍是基于单相流提出的,未考虑颗粒对壁模型的影响。本文作者团队基于Reτ=4 200的 WRLES风沙流模拟结果后验考察现有各类用于高雷诺数单相壁湍流的壁模型,发现WMLES在预测颗粒通量时存在可达 100%以上的差异。进而提出通过在积分壁模型(Integral Wall Model,IWM)[138]中引入颗粒体力项获得含颗粒影响的两相流大涡模拟壁模型,所得的WMLES结果与WRLES 结果的误差降至20%以下[128],这为高雷诺数颗粒两相流WMLES提供了重要的途径,但在积分壁模型中仍假定平均速度廓线为对数律与线性律的线性组合,而风沙流中、尤其是跃移层内流场速度廓线形式目前尚无统一结论,需要进一步研究。 WMLES也被应用于模拟大气湍流边界层中悬移粉尘地表释放和分布。如Gu等[147]模拟了半径50 m、高150 m圆柱形计算域内的尘卷风现象——一种发生在大气对流边界层内、能将沙尘或者碎屑等物体扬到高空、具有温度较高的低压核心和较短生命周期的旋风。他们基于拉格朗日方法计算了不同粒径沙尘颗粒运动轨迹,发现较小的粉尘跟随尘卷风气流,而较大沙尘由于受到离心力作用偏离主流向外运动并在旋风外围沉降,又被汇流层的高速气流携带到旋涡中心处,往复循环直至无法被上升气流扬起,进而解释了尘卷上部细颗粒富集、下部大颗粒富集的机理。Klose 和Shao[148]在美国环境预测中心(NCEP),美国国家大气研究中心(NCAR)等机构开发的 WRF(The Weather Research and Forecasting)模式的大涡模拟模块基础上发展了大涡沙尘模式,并模拟了不同风速与稳定度条件下的地表粉尘释放。Zhang等[149]数值模拟了Reτ= 3×107中性大气边界层中粉尘输运,其中粉尘采用欧拉模型模拟(式(14)),证实粉尘浓度也存在超大尺度结构,如图15所示。通过相关分析发现,浓度与流场流向速度脉动负相关而与垂向速度脉动正相关。此外,他们通过条件平均分析与象限分析揭示粉尘高低浓度区伴随流场反向旋转准流向涡对,沙尘的垂向输运与流体大尺度涡卷模式密切相关。 图15 y/H=0.05高度处流向展向平面内瞬时流向脉动速度和浓度分布模拟结果(粒径dp=10 μm)[149]Fig.15 Visualizations of instantaneous fluctuating streamwise velocity and concentration in streamwise-spanwise planes at wall-normal position of y/H= 0.05 (particle diameter is dp=10 μm)[149] 风沙运动及其引发的沙尘暴、沙丘移动等自然灾害是广受关注的环境问题。采用数值模拟方法研究风沙运动是揭示输沙机理、提高预测精度的重要手段。尽管风沙运动数值模拟从一维发展至三维、从简单轨迹计算发展至多场耦合模拟、从仅考虑平均流的雷诺平均模拟发展至考虑湍流脉动和湍流结构的大涡模拟,但仍存在需要进一步深入研究的问题和改进之处。 1) 风沙起动、击溅与湍流模型。大尺度风沙运动模拟中,地表颗粒很难单颗分辨,采用模型提供下边界条件是必然的选择。但是,目前多数基于欧拉-拉格朗日框架的风沙流模拟仍沿用了早期不精确的模型,如采用由冲击试验或基于平均流场模拟获得的击溅函数,再如沙粒的流体起动则被简单地假设为正比于平均剪切应力和临界起动应力之间的差值。而实际上,近壁(近床面)湍流速度、应力脉动对于沙尘颗粒流体起动以及冲击过程中地表颗粒的运动和溅起十分重要,目前尚未见考虑湍流影响的模型。实际沙粒地表为多种沙尘颗粒组成的混合粒径地表,而已有模型大多采用平均粒径,也是导致现有数值模拟预测结果与观测存在误差的重要原因之一。此外,沙粒运动与湍流的相互作用也影响湍流本身的统计量与结构,现有大涡模拟风沙流中所采用的亚格子模型和壁模型都是基于单相湍流提出的,尽管本文作者团队尝试考虑颗粒影响改进已有壁模型,但仍值得进一步研究。 2) 高精度、高效风沙流数值模拟方法的发展。湍流直接数值模拟或壁解析大涡模拟结合颗粒全分辨模拟或DEM方法是认识湍流输沙物理机制、准确刻画颗粒湍流相互作用、提炼流体起动规律、分析沙粒与可蚀床面冲击溅起过程的重要方法。但是所需计算量巨大。一方面,高雷诺数湍流边界层模拟既需网格足够小以解析最小湍涡,又需计算域足够大以再现对湍动能与物质输运起主要贡献的LSMs/VLSMs;另一方面,对于颗粒的精细模拟,如全分辨方法,为了解析颗粒,每一个方向颗粒上拉格朗日点数量应为~O(10),模拟所需网格量相比点力方法至少再增加2个量级。同时,无论全分辨颗粒模拟还是DEM模拟,颗粒碰撞搜索过程耗时且均需存储大量颗粒碰撞信息。因此,亟待发展低存储需求、高效、高精度的湍流风沙两相流模拟的并行优化算法,以开展更大规模的计算、获得足够的统计样本。另外还需要特别指出的是,虽然近年来,拉格朗日-拉格朗日框架下如基于光滑粒子流体动力学 (Smo-othed Particles Hydrodynamics, SPH) 方法和格子Boltzmann方法流体求解的两相流数值模拟方法[150-152]也开始发展,但对风沙运动的模拟尚处于定性一致阶段。 3) 风沙运动大尺度、跨尺度模拟的模型改进。风沙运动发生时,在垂向同时存在近地表跃移高浓度区和远离地表悬移颗粒的稀薄浓度区,本质上也是多尺度问题。已有研究主要对于跃移沙粒和悬移粉尘分别在欧拉-拉格朗日和欧拉-欧拉框架下模拟,并通过水平跃移输沙通量和垂直粉尘释放通量将二者联系起来,这种方式虽然有利于沙尘数值模式的快速预报需求,但需要引入诸多人为参数。更为重要的是,实际沙尘暴发生时,强对流流动对沙尘起动和垂向输运的影响可能比近中性条件下的剪切湍流中湍流结构本身的影响还大。在这种情况下,粉尘分布和通量预测的参数化方案中如何引入温度或稳定度等的影响还需要进一步深入研究。 4) 风沙运动数值模拟软件的开发。已有的风沙运动和典型风成地貌数值模拟工作多数采用研究者自行编制in-house代码,少数在计算流体动力学CFD软件或开源代码基础上进行二次开发。但是,现有软件如ANSYS Fluent主要的流场计算以RANS为主,虽然近年来也开发了相应LES部分,但所采用的湍流模型、壁模型等对高雷诺数大气边界层湍流的模拟仍需要检验。此外,虽然CFD软件如ANSYS Fluent也提供了多相流求解器,但由于没有考虑复杂的颗粒-可侵蚀床面的冲击溅起过程、风场-颗粒-电场多场耦合相互作用等,均不能模拟实际风沙运动和风成地貌形成演化,或需要科研人员进行长期、复杂的二次开发。2018年,中国启动了国家数值风洞(NNW)工程项目,目前已经发布多款自主研发功能先进的CFD软件系统[153]。在NNW一期基础上,开发针对风沙运动的专门软件,既可以使风沙环境相关从业人员方便地利用软件进行风沙灾害的预报与防治,也可以一定程度上加快中国CFD工业软件自主可控的进程。同时也将是NNW军民融合的一个典型范例。1 基于RANS的风沙运动数值模拟
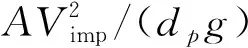





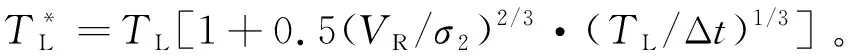
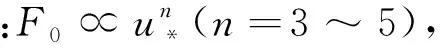
2 风沙运动的WRLES




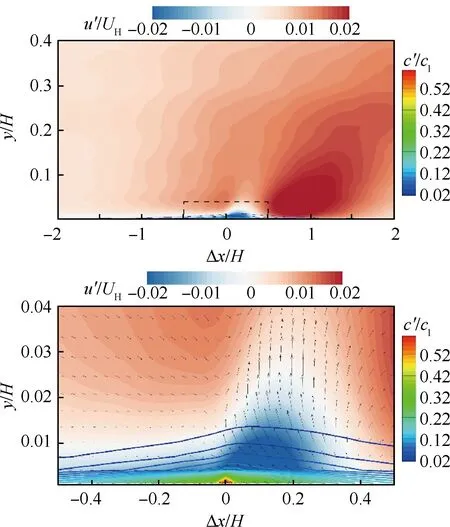
3 风沙运动的WMLES




4 结 论

