面向计算机随机信号的控制组合数学模型算法分析

李晓辉

(陕西省宝鸡教育学院科研处，陕西 宝鸡 721004 )

近年来，互联网的快速发展为人们的生活带来了许多便利。然而计算机信号的处理方法却变得越来越复杂。与周期平稳的计算机信号相比，随机信号在时域和频域都具有不确定性。由于随机信号的不确定性，往往需要采用组合数学模型进行建模，以实现对信号的处理[1]。传统的组合数学模型虽然可以完成基本的分析，但是误差比较大，精度不高[2]，因此有必要对计算机随机信号控制组合数学模型展开研究。通过将控制组合算法与数学模型相结合，可将计算机随机信号的时间特征函数转化成线性表达的数学语言[3]。本文通过实验来证明控制组合数学模型对随机信号的计算有效性，同时验证该模型的收敛速度和控制效率。

1 数字信号处理

1.1 数字信号处理技术

数字信号的幅值都是离散的，且都处于有限的数值范围内。数字信号可以由数字电路进行处理[4]，处理后抵抗外界噪声的能力增强。对于计算机输出的数字信号，需要先将其转换成离散信号。信号的数字化处理一般包含3个步骤，即抽样、量化和编码[5]。抽样的目的是将原始信号每间隔一段等量时间进行抽取，由离散的信号幅值序列代替原先时间域上的连续信号。按照奈奎斯特采样定理进行抽样[6]，可以保证还原信号与原始信号一致。信号幅值的量化是用有限个幅度值近似代替连续变化的信号值[7]。量化操作虽然可以减少量化失真，但不可避免会产生量化误差，该量化误差主要源于高阶非线性失真[8]。由于量化误差近似于噪声，因此也被称为量化噪声。当计算小幅值信号时，量化操作往往会导致信噪比很小[9]。在对信号进行量化操作后，对信号进行编码，将信号转换成数字编码脉冲。数字信号处理流程具体如图1所示，其中X(t)表示时间域下的连续信号，X(n)表示频域下的离散信号。

图1 数字信号处理流程

在数学算法分析领域，组合数学是重要的研究内容之一，组合数学的研究对象是有限、离散的数学结构，其内容如图2所示。在算法设计中，一般会用到分治算法、分支限界法、回溯法和动态规划等，先将计算机的随机信号进行离散化处理，然后将其变换成一维空间向量，再分别对宽度向量和延时向量进行逻辑运算，输出离散状态的向量序列。

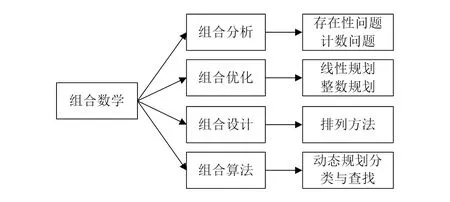
图2 组合数学内容

1.2 随机信号传统处理方法

随机信号的传统处理方法主要用于分析随机信号的相关函数与协方差函数。首先研究概率分布函数，假设tn为时间变量，xn为随机变量，T为时间变量集合，R为随机变量的样本空间。当t1,t2,…,tn∈T,x1,x2,…,xn∈Rn时，n个随机变量X(t1),X(t2),…,X(tn)的n维联合概率分布函数为：

(1)

式中：f(x1,x2,…,xn;t1,t2,…,tn)为n个随机变量的概率密度函数，通过n维联合概率分布函数对n个随机变量求导数可得。

其次分析概率密度函数，n维随机变量的概率密度函数是指对于联合概率分布函数，存在非负可积的函数在积分后可得到联合概率分布函数，那么该非负可积的函数称为概率密度函数。概率密度函数表示概率分布函数在该点的变化率。概率分布函数的概率密度函数为：

f(x1,x2,…,xn;t1,t2,…,tn)=

(2)

假设任意j个时刻tj(t1,t2,…,tj∈T)，存在j个随机变量xj(x1,x2,…,xj∈Rj)，各随机变量具备独立统计性时，其联合概率分布函数为：

(3)

2 组合数学模型算法建模设计

2.1 数学模型建立

随机信号在通常情况下不具有傅里叶变换的性质，因此计算机随机信号的总能量在理论上是无限的[10]，仅可以计算出一段时间内的能量谱，即功率谱。随机信号一般可分成平稳信号与非平稳信号。根据数学理论，可以计算出平稳随机信号功率谱的估计值，功率谱密度函数G(f)为：

(4)

式中：T2，T1为信号x(t)的时间点；x(t)为平稳随机信号；f为信号频率；t为时间域上的积分时间。自相关函数通过傅里叶变换为功率谱密度函数。自相关函数具有偶函数的特性，功率谱密度函数经过变换后，其表达式如式(5)所示，该式也是功率谱常见的表达形式。

(5)

式中：R(τ)为x(τ)的自相关函数；τ为频域中的频率变量。非平稳信号的功率谱可以通过逐段求解的方式得到。随时间变量变化的功率谱向量被称为时变功率谱。依据计算机随机信号建模原理，利用差分函数定理可得差分数学模型。某一个时间段内随机信号的差分模型如式(6)所示：

(6)

式中：x(r)为计算机随机信号的差分函数；α1为信号的随机阻力值；r为随机信号的数量；ω(r)为阻力值的零均值；p为随机信号传播的阶数。将随机信号的表达式进行转换，让随机信号具备组合数学特征，随机信号的线性表达式如下：

(7)

式中：αm为权重系数。在时间域上构建控制组合数学模型，在t时刻下，该数学模型的函数p(t)为：

p(t)=[f0(q-k)x+q+k]

(8)

式中：f0为随机信号的基函数；q，k为随机信号的个数。计算机随机信号的参数矢量与控制组合数学模型的控制能力呈现较强的相关性，越稳定的参数矢量，其控制性越好，越有利于提高控制组合数学模型的精度。因此参数矢量的稳定性决定了控制组合模型的准确度，矢量的阶次表征该模型的线性特征参数。

2.2 算法设计

在算法设计之前，首先分析随机信号的频率谱和时变谱。采用自适应算法对随机信号的线性特征进行组合。针对随机信号，利用组合数学控制建模的方式，归纳出计算机随机信号的跟踪函数。假设该函数的跟踪因子为λ，那么阶次等于0的随机信号跟踪函数K0(m)：

K0(m)=P(m-1)H′(λ)

(9)

式中：m为随机信号数；P为遗忘因子；H′为跟踪性能差。随机信号控制算子K(t)为：

(10)

式中：λ(m)为m个随机信号的跟踪因子。通过最小二乘法适当地简化计算步骤，从而可以计算出相应的函数方程。跟踪函数可以实现对随机信号的精准跟踪。该控制组合算法可以快速地完成对随机信号的无失真控制，对随机信号的处理效果十分明显。

3 实验设计与结果分析

为验证算法的有效性与准确性，对处理后的计算机随机信号进行建模验证。严格控制实验变量，保证其不影响实验结果。实验采用相同时间函数特征信号x(g)，其表达式为：

(11)

式中：ω(g)为时间函数的零均值；g为时间变量。在计算过程中，采用对比实验方式对不同算法进行比较，对比组采用传统的数学模型算法，考察算法的控制精度与收敛速度。标准差是重要的指标，尤其对于非平稳随机信号来说是至关重要的。由于算法计算量过小会导致实验对比效果不明显，但迭代次数过大又会导致算法速度降低，因此算法迭代的次数也是考察的指标。迭代次数在本实验中设置为500～800次。实验论证结果对比见表1。

表1 算法的实验论证结果对比

实验结果表明，采用固定参数差分函数的控制组合数学模型可以对随机信号进行有效控制，该模型具备很大的计算优势。该实验结果也说明控制组合数学模型可以实现对随机信号的无失真控制。从收敛时间来看，控制组合数学模型的收敛速度明显更快，跟踪控制的时间更短。通过标准差可以看出，该控制组合数学模型的准确性和稳定性也相对较好。

4 结束语

本文从数字信号处理的角度出发，针对计算机随机信号的时变谱特征，结合组合数学的建模算法，构建了相应的控制组合数学模型。本文对控制组合数学模型的算法进行了设计，保证了处理后的随机信号具备良好的线性特征。对比实验分析表明，相比于传统数学模型，该控制组合数学模型算法具备良好的计算有效性，并且在控制精度方面也有很大的提升，验证了该控制组合数学模型的有效性，并对其准确性进行了分析。本文研究的控制组合数学模型为随机信号的后续研究提供了合理的实验依据，对该领域的发展具有积极的指导意义。